基于改进PID算法的CFB锅炉床温控制

张静 张瑞青

摘  要：床温是循环流化床锅炉保持经济、安全运行的重要参数，对床温进行优化控制可以提高锅炉运行的效率。针对床温具有非线性、时变、多变量耦合的特点，常规PID控制已无法达到良好的控制要求，采用粒子群算法对PID进行改进，并在Matlab软件平台上仿真，结果表明，粒子群改进PID算法对床温的控制效果比常规PID控制的稳定性、准确性、快速性更好。

关键词：循环流化床锅炉;床温;PID算法;粒子群改进PID算法;Matlab仿真

中图分类号： TP273              文献标志码：A

循环流化床（Circulating fluidized bed， CFB）锅炉具有对燃煤的利用率高、低污染以及负荷调节性能好的特点，因此得到了快速发展与广泛应用[1]。床温过高或者过低会直接影响CFB锅炉的运行效率，所以必须将床温控制在一定范围内[2]。传统PID控制算法对CFB床温的控制效果已经满足不了日益提高的控制要求，但是PID算法简单、应用广泛，所以研究改进PID算法对床温进行控制具有重要的意义。

1 粒子群改进PID算法

粒子群算法是模仿鸟类捕食的过程：若干只鸟在一定区域内寻找食物，每只鸟都知道整个鸟群目前所搜索的所有位置，根据这些位置，鸟类自行判断改变自己的搜索方向，经过一定时间的搜索后，小鸟会距离食物越来越近，最終找到食物的位置。每只鸟即为粒子。在鸟类捕食的过程中，鸟类会自行判断自身位置相对于食物位置的优劣性来决定自身的飞行方向，而在粒子群算法中，用适应度函数来衡量粒子位置的优劣性，根据适应度函数值粒子决定自身位置的变化方向，向当前的最优解运动[3]。

粒子群寻优步骤是：首先初始化粒子群，将粒子随机分布在搜索空间内，根据适应度函数计算每个粒子的适应值，即个体极值，通过个体极值的对比，找出当前所有粒子的最优解，即全局极值。所有的粒子都会向全局极值的位置运动，在运动的过程中，个体极值和全局极值会不断变化，粒子的运动也随之不断地变化，在一定时间后，所有的粒子都会聚集在某一个点的附近，这个点就是所寻找的最优解[4]。

PID控制器参数的优化问题，即取得kp，ki，kd  3个参数的最优值，使控制系统的控制效果达到最佳。适应度函数是评价粒子群粒子好坏的重要标准，选取不同的适应度函数会直接影响系统优化的最优解，时间误差绝对值积分在PID控制系统的性能评价指标里是使用最普遍的一种，不但可以减少误差对输出响应的影响，而且可以使偏差调节作用增加，具有结构简单、震荡幅度适中等特点，所以选取时间误差绝对值积分作为粒子群算法的适应度函数[5]。

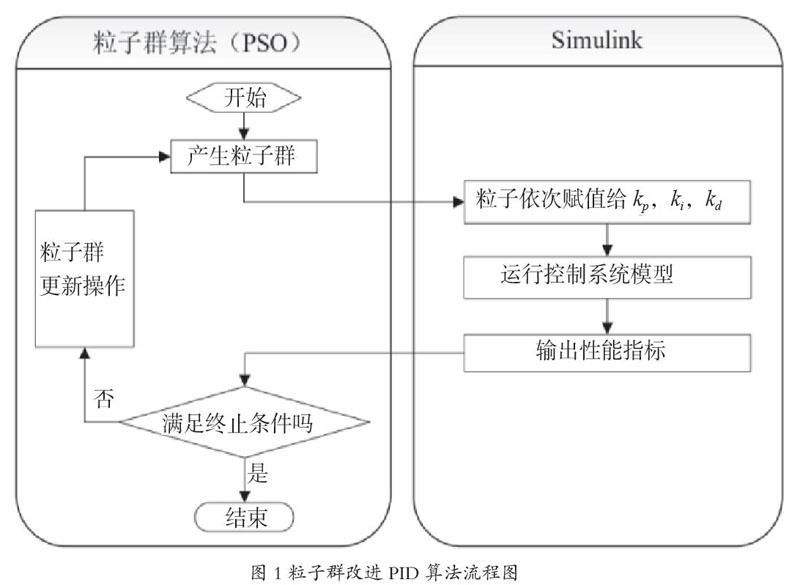
基于粒子群算法优化PID参数的流程：首先，粒子群初始化，产生随机粒子，然后将随机粒子的值赋予PID控制器的kp，ki，kd  3个参数，针对该参数使系统模型运转，得到此时的适应度函数值，将该值作为输出，输入判断模块，如果不满足终止条件，则粒子群进行更新，再次赋予PID的3个参数进行运算，如果满足终止条件，则退出循环输出最优值。粒子群改进PID算法流程图如图1所示。

2 CFB机组床温控制

2.1 PID床温控制

传统PID控制器的结构层次和控制原理相对简单，实现难度低，可用于多种被控对象、多样的控制环境，所以，传统的PID控制器普遍地应用于CFB锅炉的控制系统中。

CFB机组PID床温控制系统为单回路控制系统，采用调节给煤量来调节CFB床温，工作原理如图2所示，R 是床温的设定值，Y 是床温的测量值，用温度变送器采集床温的数值送入调节器，形成一个单回路控制策略。

给煤量与床温之间的影响关系用传递函数来表示：

式中：s代表t时间域映射到复数域中的复数变量，G（s）为传递函数，即床温的复数域模型。

在MATLAB的Simulink仿真软件中搭建PID单回路控制系统，主要用到的仿真模块有阶跃信号模块、PID控制器模块、传递函数模块、延迟模块以及示波器模块，进行连接后仿真。

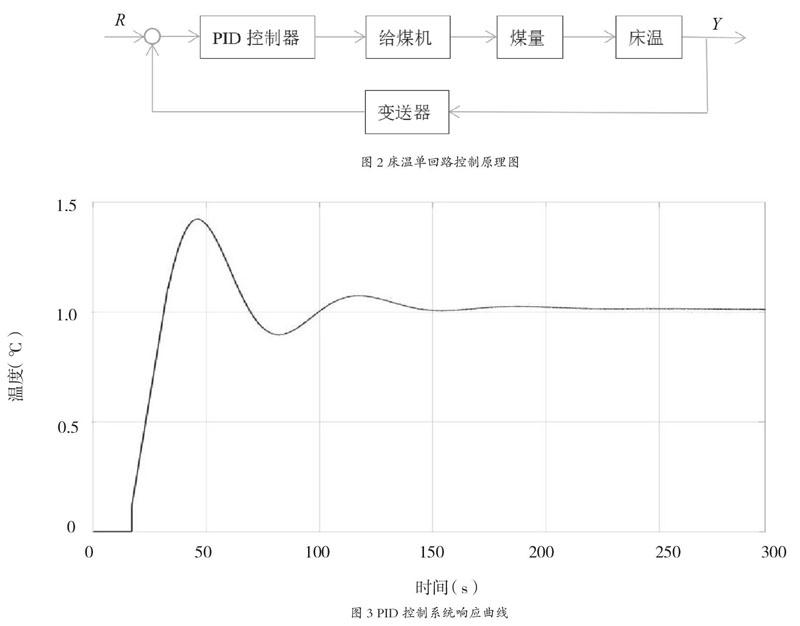
PID参数整定方法利用临界比例带法，先将系统置于单纯比例控制的条件下，通过仿真得到系统的临界比例带和临界震荡周期，然后再根据经验公式求出PID控制器的各参数值，最后再调整各个参数达到良好的控制效果。通过对PID参数的整定，PID参数设置为kp=1.205，ki  =0.005，kd=2.34。PID床温系统的仿真曲线如图3所示，横坐标范围为0 s～300 s，每格代表50 s;纵坐标范围为0 ℃～1.5℃，每格代表0.5℃。从图中可得：系统超调量为42.3%，上升时间为46 s，调节时间为210 s。

2.2 粒子群改进PID床温控制

在粒子群算法算法中，设置群体规模为10，，最大迭代次数为100。通过粒子群算法对PID的kp，ki，kd  寻优，将寻优找到的最优值kp=1.042、ki=0.001、kd =4，代入PID控制器，系统响应曲线如图4所示，横坐标范围为0 s～300 s，每格代表50 s;纵坐标范围为0℃～1.2℃，每格代表0.2 ℃。从图4中可得：系统的超调量为16.7%，上升时间为44 s，调节时间为135 s。

对比图3与图4仿真控制系统曲线，粒子群改进PID算法后的控制系统超调量从改进前的42.3%下降到16.7%，控制系统更平稳、无大的波动，生产过程更平稳;上升时间由改进前的46 s下降到44 s，控制系统反应更快，快速性得到提高;调节时间由改进前的210 s缩短到135 s，说明系统在受到阶跃信号作用后能更快速地过渡到稳定状态。

3 结论

针对传统PID算法无法满足当今CFB床温控制要求，该文设计粒子群改进PID算法的床温控制系统，通过Matlab仿真得出：粒子群改进PID算法的床温控制响应曲线与传统PID控制床温的响应曲线相比较，系统的超调量减小，系统更平稳，调节时间缩短，系统能更快的达到稳定状态。

参考文献

[1]郑守忠，张勇.循环流化床锅炉床温影响因素的试验研究[J].热力发电，2007（9）：36-38.

[2]陈亮.循环流化床锅炉床温控制系统的应用研究[D].北京：华北电力大学，2013.

[3]谢晓锋，张文俊，杨之廉.微粒群算法综述[J].控制与决策，2003， 18（2）： 129-134.

[4]杨智，陈颖.改进粒子群算法及其在PID整定中的应用[J].控制工程，2016（2）：161-166.

[5]吴垚，霍亮生，黎进远，等.自适应混沌粒子群算法及在PID整定中的应用[J].计算机仿真， 2014（8）：377-381.