用PID控制近似线性自抗扰控制

崔文庆，王雨桐，谭 文

(华北电力大学控制与计算机工程学院，北京 102206)

1 引言

现如今，随着先进控制理论的快速发展，很多先进控制策略在各行各业广泛应用.但是在工业控制过程中，PID仍然占据主导地位，主要原因是有些先进控制策略难以调试，硬件难以实现等诸多问题.而PID控制结构简单、稳定性好、易于整定，只需调整3个参数即可，即比例增益P(确保快速性)、积分增益I(确保稳态误差为零)和微分增益D(改善对象动态特性).PID控制器的这3个参数直接与系统控制性能相关，在不知道被控对象特性的情况下，也可以进行在线参数调整.但PID控制也有自身的缺陷，因为PID控制是基于误差反馈的控制策略，即只有产生了误差，控制器才会动作，在有些工业工程中，大迟延系统十分常见，因此PID的局限性是显而易见的.因此，为了取代PID控制，新型控制方法应该具有如下特征:

1)结构固定，在实际工业工程中容易实施;

2)调节参数少，且控制率简单，便于控制工程师理解和调整参数，每个参数与闭环系统性能都有关系;

3)能够实时预测或估计输出与设定值之间的误差，从而达到更好的控制性能.

而在先进控制理论的发展中，很少有控制方法具有所有这些特性，这就是PID控制仍然占据主导地位的原因.

自抗扰控制(active disturbance rejection control，ADRC)是由韩京清研究员在20世纪90年代提出的一种新型控制方法，结合了非线性PID、跟踪微分器、扩张状态观测器等研究成果[1-2].ADRC最大的特点就是不需要知道被控对象的精确模型，只需要知道对象的相对阶和高频增益即可.ADRC的原理十分简单，就是将被控对象的内部扰动和外部扰动当做“广义扰动”，利用扩张状态观测器(extended state observer，ESO)估计和补偿扰动，然后利用状态反馈控制率进行控制.目前自抗扰控制在各个工业领域均有应用.例如，在电力生产过程中，文献[3]讨论了ADRC在光伏发电系统中的应用;文献[4]研究了ADRC在负荷频率控制中的应用;文献[5]将ADRC应用在超临界机组协调控制系统中;文献[6]研究了ADRC在火电机组DCS中的应用等.

而在实际应用过程中，非线性自抗扰控制结构十分复杂，需要整定的参数较多，限制了其在实际中的推广.高志强教授为了克服上述限制，提出了自抗扰控制的线性版本(linear active disturbance rejection controller，LADRC)[7]，极大地简化了ADRC 的结构.同时，为了便于整定LADRC，高老师又提出了带宽整定法[8]，将LADRC整定参数的选取归结为控制器带宽和观测器带宽的选取.类似于PID控制，LADRC具有固定结构，参数可以由2个或3个参数整定得到，因此LADRC是替代PID控制的理想技术.

自从ADRC提出以来，该方法与PID控制之间的关系就得到广泛关注.文献[2]从原理上分析了PID和ADRC的关系;文献[9]证明2阶LADRC实际上是PID加2阶滤波器的结构;文献[10]讨论了将PID转化为2阶LADRC的方法;文献[11]分析了LADRC的通用性，并提出将PID转化为基于带宽的2阶LADRC的方法.文献[12]分析了扰动观测器(DOB)、SPID和ADRC在估计系统不确定性上的异同;文献[13]提出了一种基于现有PID参数整定多变量系统LADRC参数的方法;文献[14]从经济学的角度分析了ADRC和PID的区别，并分析了ADRC的应用前景;文献[15]提出了一种PID和ADRC之间相互转换的公式;文献[16]比较了ADRC和PID在扰动抑制方面的区别，并对自抗扰控制的核心思想进行了阐述.上述文献表明LADRC具有比PID更广泛的结构，PID可以认为是2阶LADRC的一种特殊情况.

既然PID 可以转化为LADRC，那么反过来，能否从LADRC得到PID?本文首先证明LADRC的积分作用实际上包含在扰动的估计及补偿里，进一步说明了2阶LADRC和PID的关系;紧接着对于各阶LADRC，本文提出了实际PID+n阶超前环节的近似方法.仿真结果表明，对于2阶和3阶LADRC，分别采用实际PID和实际PID+1阶超前环节的方式就可以取得非常不错的效果，但对于4阶LADRC，实际PID+2阶超前环节的策略已经可以在中频尽可能接近原4阶LADRC，但是对于具体实例的控制效果还是不如4阶LADRC.因此，高阶LADRC弥补了PID控制的缺陷，在工业过程控制中具有更好的应用前景.

2 线性自抗扰控制

2.1 结构

线性自抗扰控制器无需知道被控对象的精确模型，仅需知道被控对象的相对阶r和增益b即可.因此假设被控对象模型有如下表述:

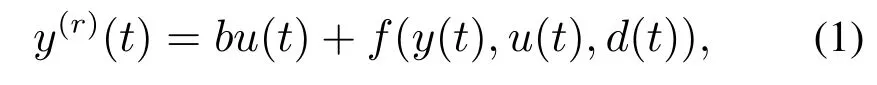
式中f(y(t)，u(t)，d(t))表示系统广义扰动，包含了系统的外部扰动和未建模动态.

LADRC的基本思想是用扩张状态观测器估计系统输出的各阶导数和广义扰动.令

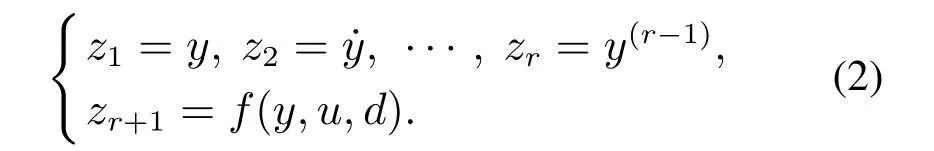
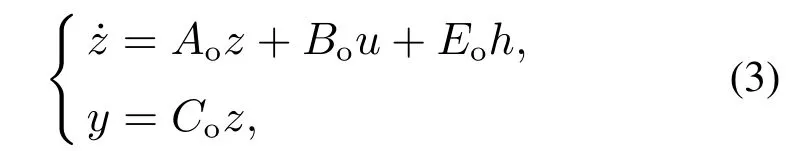
式中:z=[z1z2z3··· zrzr+1]T，

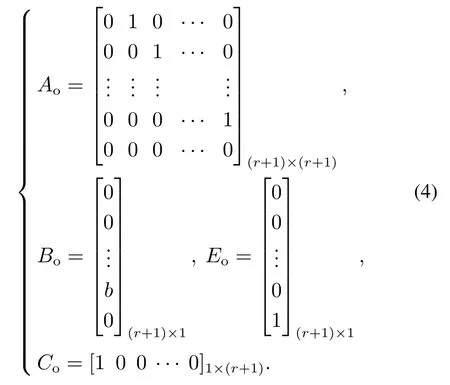
针对以上系统，设计Luenberger观测器:

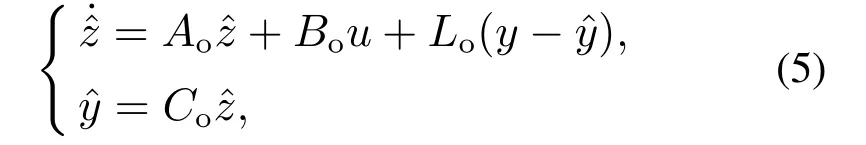
式中Lo为观测器增益:

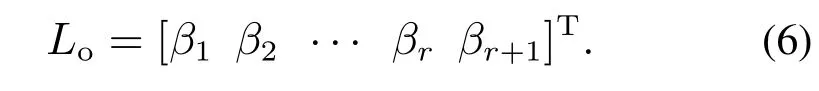
当Ao－LoCo渐近稳定时，分别趋近于y，···，y(r-1)，f(y，u，d).若将控制率定义为

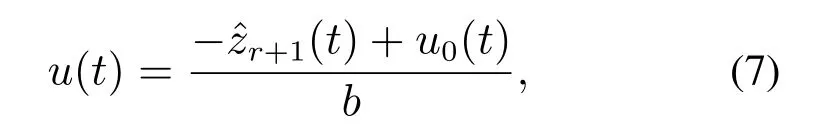
式中u0待定，则式(1)变为

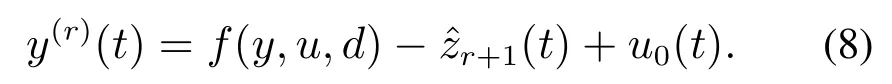
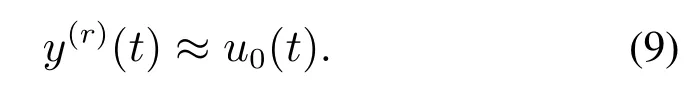
此时选取如下状态反馈率:

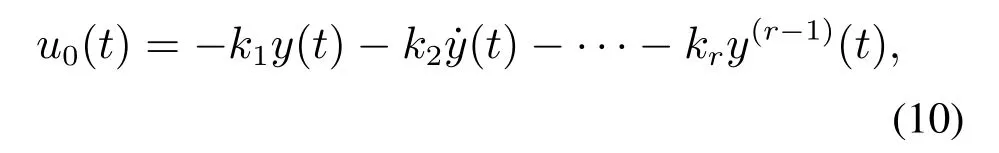
从而最终控制率可以表述为

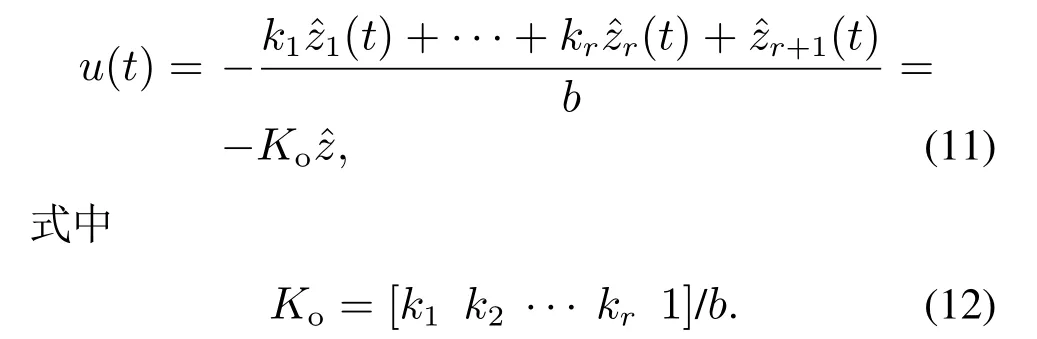
因此LADRC状态空间实现可以总结为

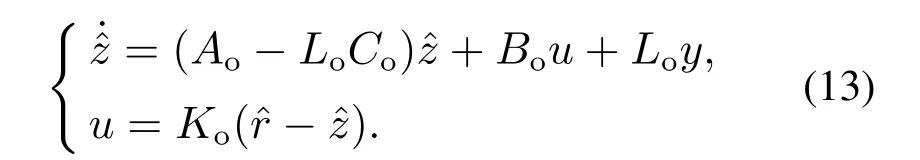
其结构图如图1所示.

图1 线性自抗扰结构图Fig.1 Structure of LADRC

2.2 参数整定

通过上述分析可知:LADRC的整定实际上就是控制器增益和观测器增益的选取问题.而目前通用的整定方法就是高志强教授提出的带宽法，将控制器增益和观测器增益的选取变为二者带宽的选取.针对扩张状态观测器，其特征方程可以描述为

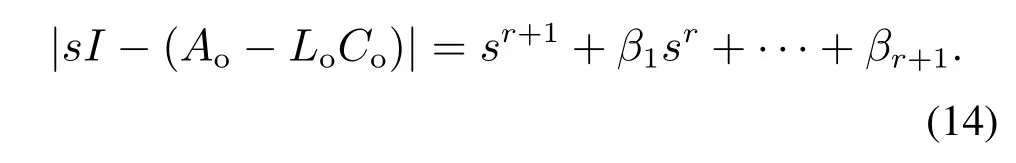
若将扩张状态观测器极点都配置到－ωo，则有

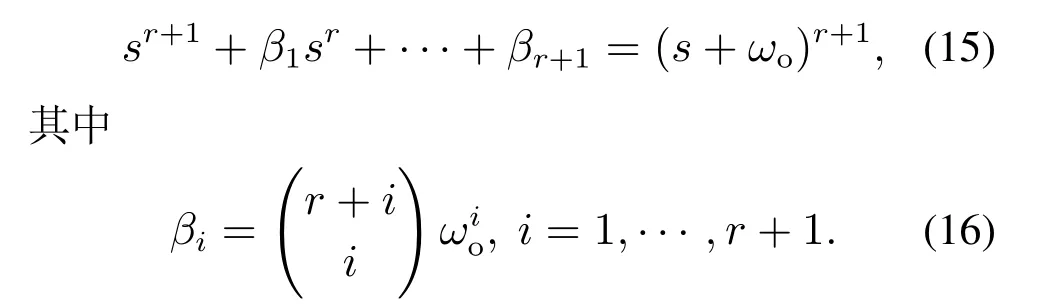
只要观测器带宽ωo选取适当，就可以得到观测器增益，扩张状态观测器就可以估计系统输出及输出各阶导数和总扰动，由上分析可得，系统就可以被看做积分对象.而闭环系统特征方程为

只需将其余的极点配置到－ωc即可.

因此改变控制器带宽ωc，就可以调整控制器增益Ko.

3 2阶LADRC结构分析

综合控制器性能、整定及实现等各方面因素，实际中LADRC常采用2阶形式.对于2阶LADRC，Lo=[β1β2β3]T，Ko=[kpkd1]/b，，从而其线性扩张状态观测器为

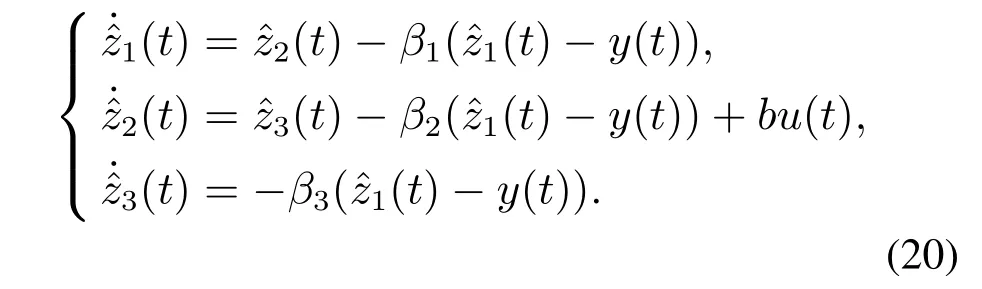
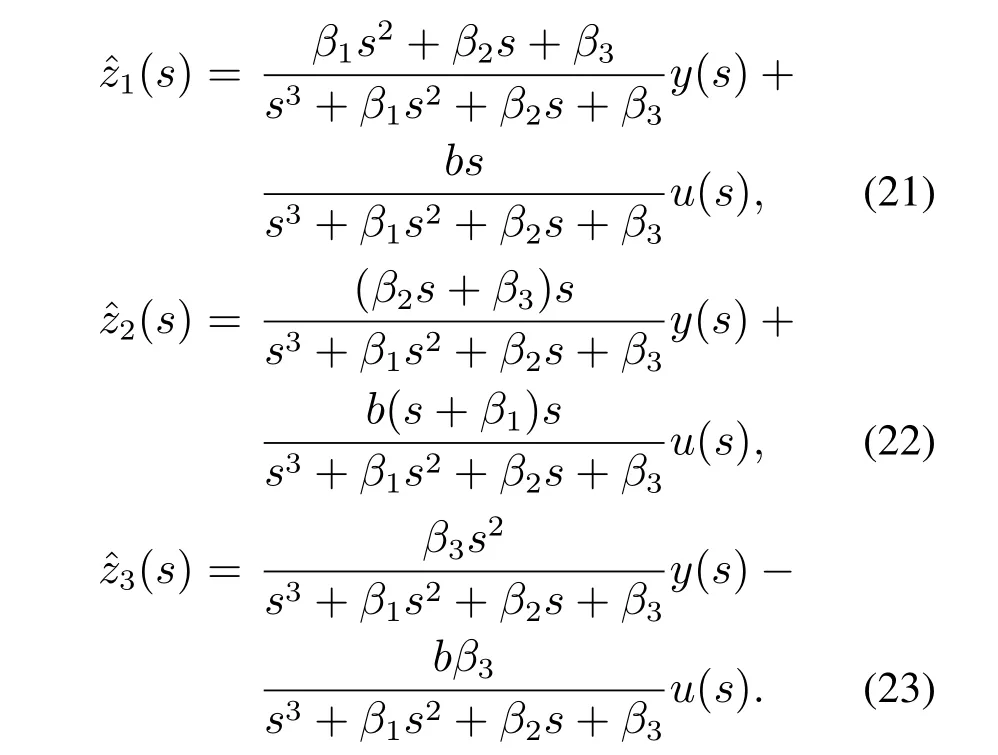
由式(10)-(12)可得，2阶LADRC的反馈控制率为

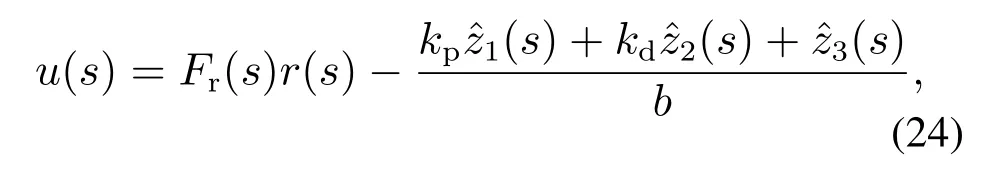
其中Fr(s)为参考输入r(t)到的传递函数.将式(21)-(23)代入式(24)可以得到y(t)到u(t)的传递函数(即控制器传递函数Kc(s)):

再将式(25)代入式(21)-(23)可以得到y(t)到，的传递函数:

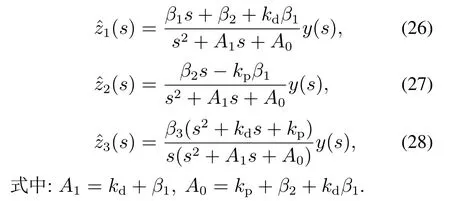
式(24)表明2 阶LADRC 实际上就是P+I+D 的组合，但是与常规的PID 控制器的直接组合不同，2 阶LADRC没有直接采用输出的导数及积分，而是利用ESO，对输出的导数及积分进行了估计，然后再进行线性组合.因此，不能直接由式(24)得到等价的PID控制器参数.

另一方面，由式(25)可知，2阶LADRC实际上是由一理想PID+2阶滤波器构成[9].显然可以直接忽略2阶滤波器可以得到1个理想PID控制器，但是，该控制器不能保持原2阶LADRC控制器的对噪声抑制的性能，因此并不是原2阶LADRC的很好近似.本文将根据2阶LADRC的结构，得到性能近似的实际PID控制器参数.

4 由2阶LADRC得到PID控制器参数

对于一个任意带积分作用的3阶严格正则控制器，其传递函数一般形式可以写成

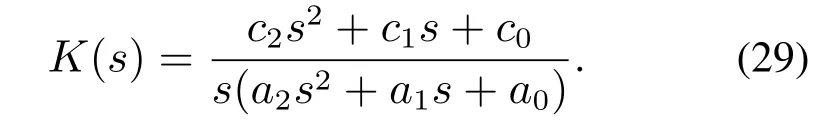
本文目的是将其近似成如下实际PID形式:

其中:Kp是PID控制器的比例增益，Ti为积分时间，Td为微分时间，Td/N为微分滤波时间.由于式(29)分母为3阶的，而式(30)分母为2阶，因此为了用式(30)逼近式(29)，可以把式(29)中分母的高阶项a2s2去掉，得到如下近似:

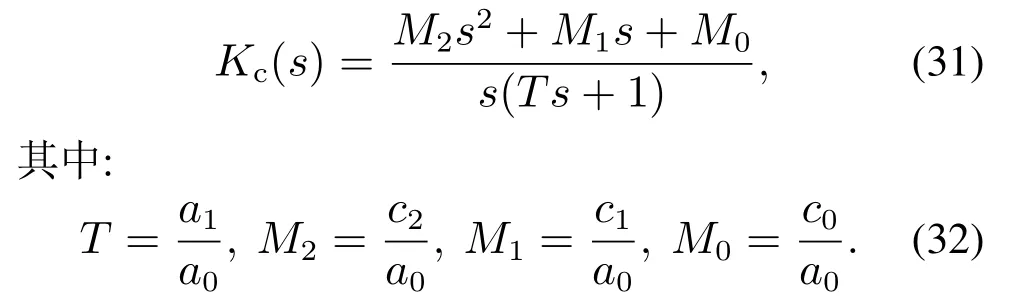
将式(30)通分化简得到

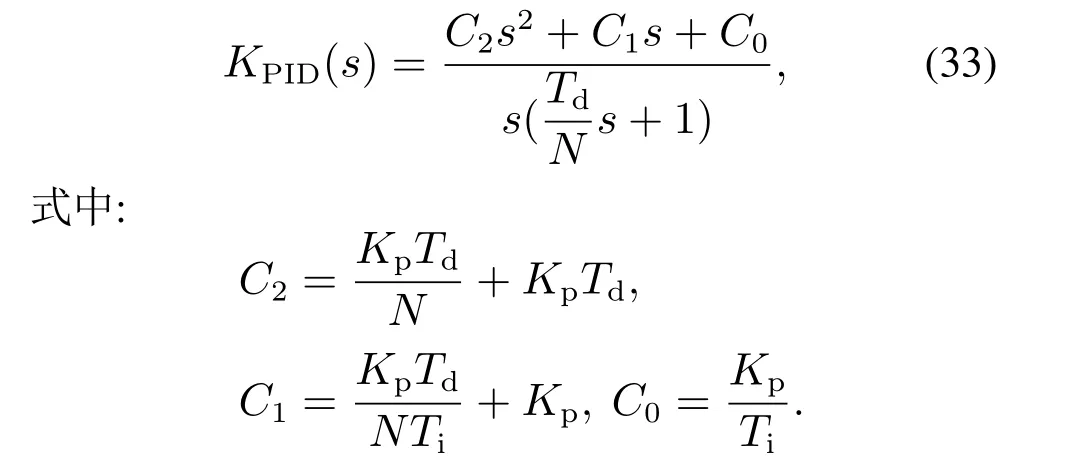
比较式(31)和式(33)，可以得到

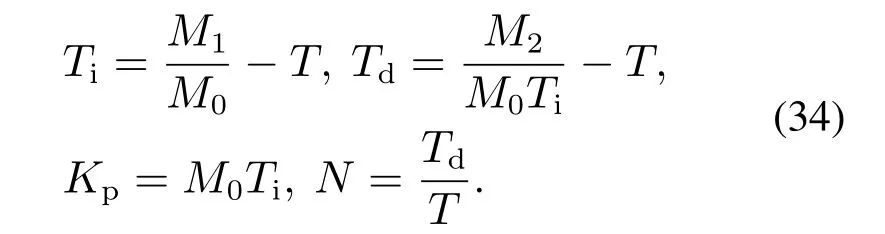
2阶LADRC的传递函数(25)可以写成带积分的3阶严格正则形式，从而可以由式(34)导出近似的实际PID控制器的参数.

例1对于被控对象，采用文献[17]的2阶自抗扰控制器参数整定法，得到2阶LADRC控制器参数:ωc=8.22，ωo=5.58，b=15.93.由式(25)可以得到该2阶LADRC控制器反馈环的传递函数:

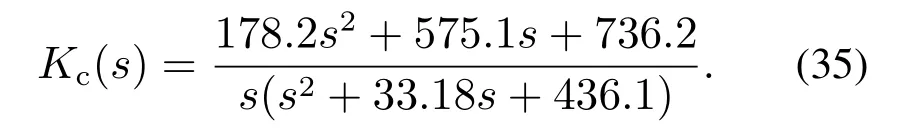
由本文方法，可以得到近似的实际PID参数:

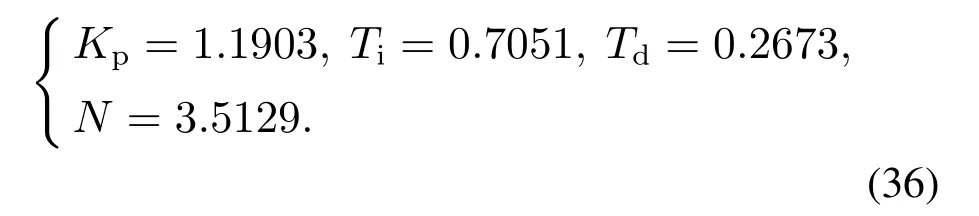
而忽略2阶滤波器可以得到理想PID控制器参数:

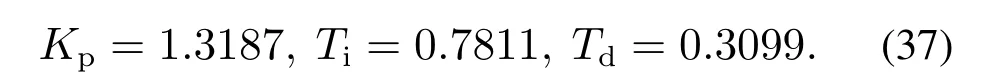
图2给出2阶LADRC(35)、实际PID控制器(36)、理想PID 控制器(37)的Bode图.为了公平，理想PID控制器(37)也按实际PID控制器实现，其中N和(36)的取值相同.可以看到，本文方法得到的实际PID在中低频段与原2阶LADRC控制器更接近.

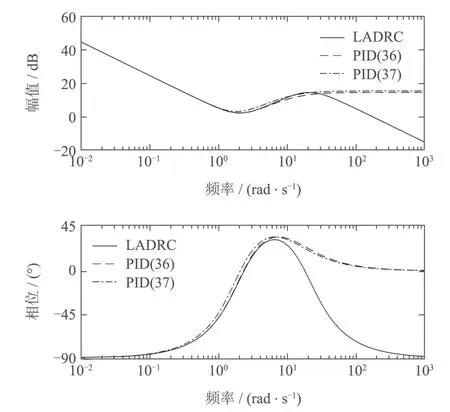
图2 例1系统LADRC和PID的Bode图对比Fig.2 Comparison of the Bode plots of LADRC and PID for Example 1

图3显示的是t=1 s加入幅值为1的设定点阶跃信号以及t=20 s输入端加入幅值为0.5的阶跃扰动时例1系统在不同控制器下的响应.可以看到，三者具有相似的抗干扰性能.但是由本文方法得到的实际PID(36)的响应更接近原2阶LADRC控制器.

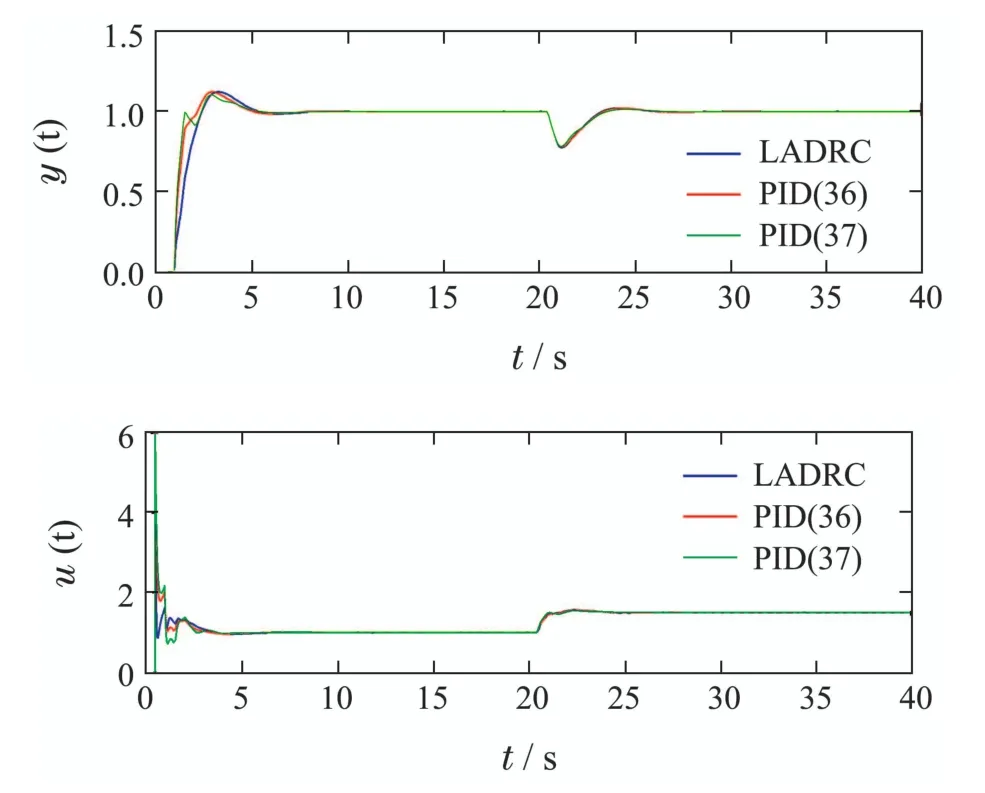
图3 例1系统在LADRC及PID下的响应Fig.3 Responses of Example 1 under LADRC and PID

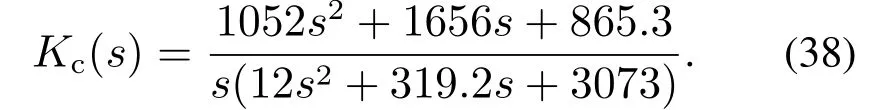
由本文方法，可以得到实际PID参数:

而忽略2阶滤波器可以得到理想PID控制器参数:

图4给出2阶LADRC、实际PID控制器(39)、理想PID控制器(40)的Bode图.为了公平，理想PID控制器(40)也按实际PID控制器实现，其中N和式(39)的取值相同.可以看到，本文方法得到的实际PID在中低频段与原2阶LADRC控制器更接近.

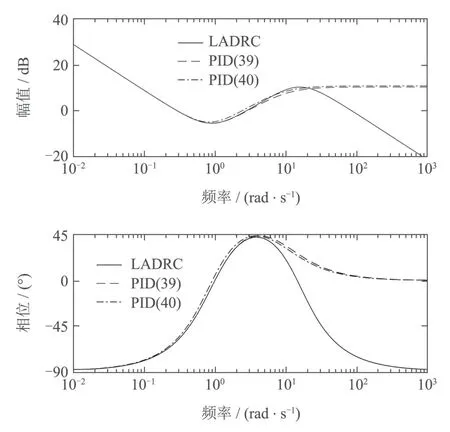
图4 例2系统LADRC和PID的Bode图对比Fig.4 Comparison of the Bode plots of LADRC and PID for Example 2

图5显示的是t=10 s加入幅值为1的设定点阶跃信号以及t=40 s输入端加入幅值为0.5的阶跃扰动时例2系统在不同控制器下的响应.可以看到，3者具有相似的抗干扰性能.但是由本文方法得到的实际PID(39)的响应更接近原2阶LADRC控制器.

图5 例2系统在LADRC及PID下的响应Fig.5 Responses of Example 2 under LADRC and PID

5 由高阶LADRC得到PID控制器参数

类似于2阶LADRC，高阶LADRC通过ESO估计对象输出的各阶微分及扰动(输出的积分)，然后通过线性组合得到一种PID(n)的控制结构，是2阶LADRC的扩展.显然，高阶LADRC已经突破了PID控制结构的局限性，利用了输出的更高阶微分，因此可以取得比PID控制器更好的性能.

为了从高阶LADRC得到近似PID控制器的参数，可以采用文献[19]提出的频域近似法，将任意阶带有积分行为的严格正则的控制器Kc(s)近似为PID形式，在低频和中频上让两个控制器尽可能一样，从而使得原控制器Kc(s)和近似后的PID控制器控制抗低频干扰效果近似.频域近似法的步骤如下[19]:

1)给定控制器Kc(s)，得到一个频率范围，计算Kc(s)的频率响应Kc(jω);

2)找出使得Kc(jω)的幅值达到最小值的频率ωz;

3)将Kc(s)近似为如下PID：

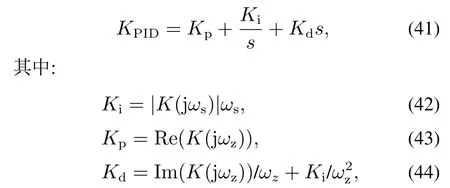
ωs取一个任意小的频率即可.

上述步骤相当于在频域上采用PID控制器去近似Kc(s)，其中PID控制器和Kc(s)具有相同的积分性能和转折点，最终求得PID保留了Kc(s)从低频到中频范围的幅值，从而能保证PID 抗低频干扰性能接近于原控制器Kc(s).

由于PID控制器仅为2阶，因此有时相位不能很好逼近原高阶控制器，为了更好的近似，可以考虑PID的一种扩展形式，即PID+超前环节形式:

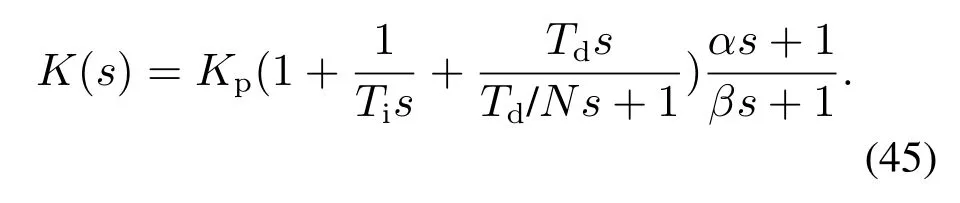
对于3阶LADRC，其传递函数可以写成如下带有积分的4阶传递函数形式:

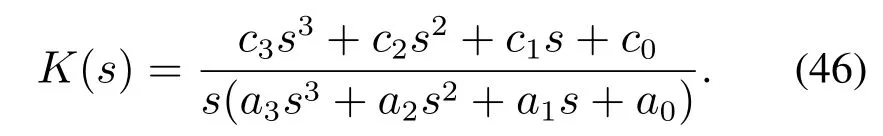
式(46)中分子多项式为3阶，因此存在3个根.由于系数为实数，因此必有一根为实数，因此分子多项式可以分解成(α2s2+α1s+α0)(αs+1)的形式.类似地，式(46)分母多项式也可以分解为s(β2s2+β1s+β0)(βs+1)的形式，忽略β2s2项，可以将式(46)转化为如下形式:

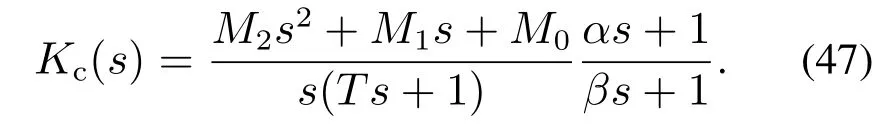
将式(45)通分并化简得到

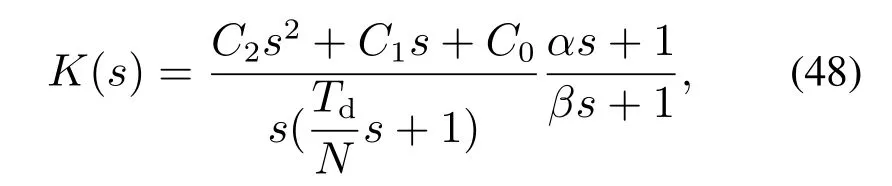
式中C2，C1，C0由式(33)所示.比较式(47)和式(48)，就可以得出式(45)中各系数的取值，其中Kp，Ti，Td，N可由式(34)获得，－1/α，－1/β分别是式(46)中分子和分母两个3次多项式的实根.

例3考虑图6所示的电力系统非再热汽轮机负荷频率控制问题.图中为调节阀动态;为汽轮机动态;为负荷及电机动态，为机组下降特性.模型参数如下:Kp=120，Tp=20，Tt=0.3，Tg=0.08，R=2.4.

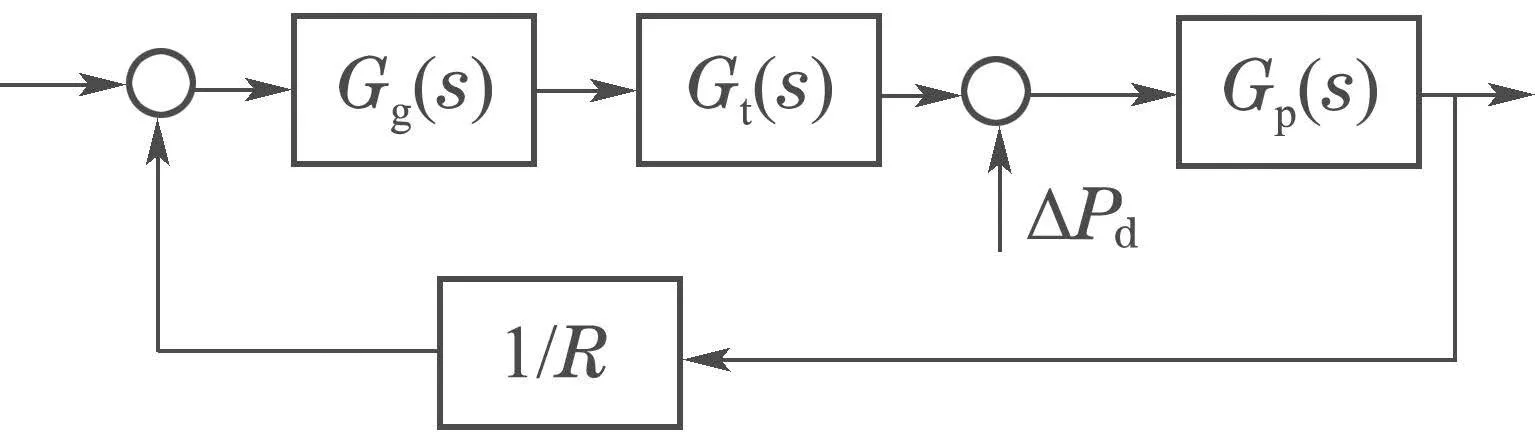
图6 电力系统负荷频率结构图Fig.6 Load frequency structure diagram of power system

文献[20]对上述系统设计了一个3阶LADRC，参数为ωc=4，ωo=30，b=250，取得了不错的抗负荷扰动ΔPd效果.本文考虑将该3阶LADRC用PID近似.

由LADRC 状态空间表达式(5)可以得到该3 阶LADRC控制器的反馈环传递函数:

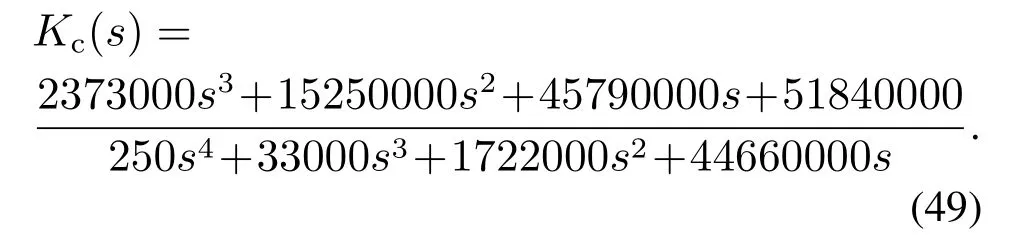
通过上述频域近似法式(42)-(44)可以将其近似为理想PID控制器，参数为

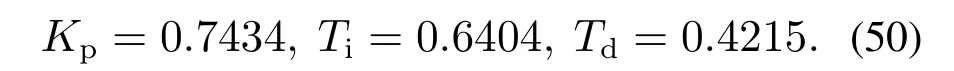
采用PID+超前环节形式(45)，得到参数

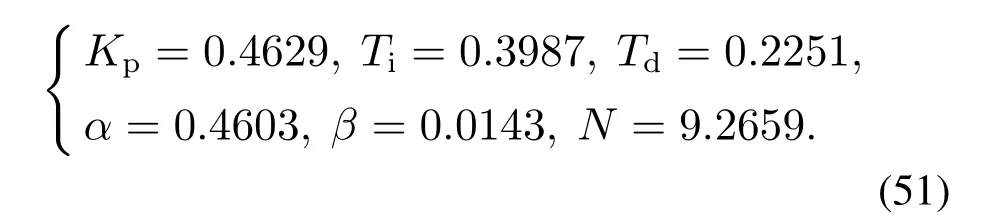
图7给出3阶LADRC、PID+超前环节(51)、PID控制器(50)的Bode图.为了公平，PID控制器(50)也按实际PID控制器实现，其中N和式(51)的取值相同.可以看到，PID+超前环节(51)在中低频段与原3阶LADRC控制器更接近.

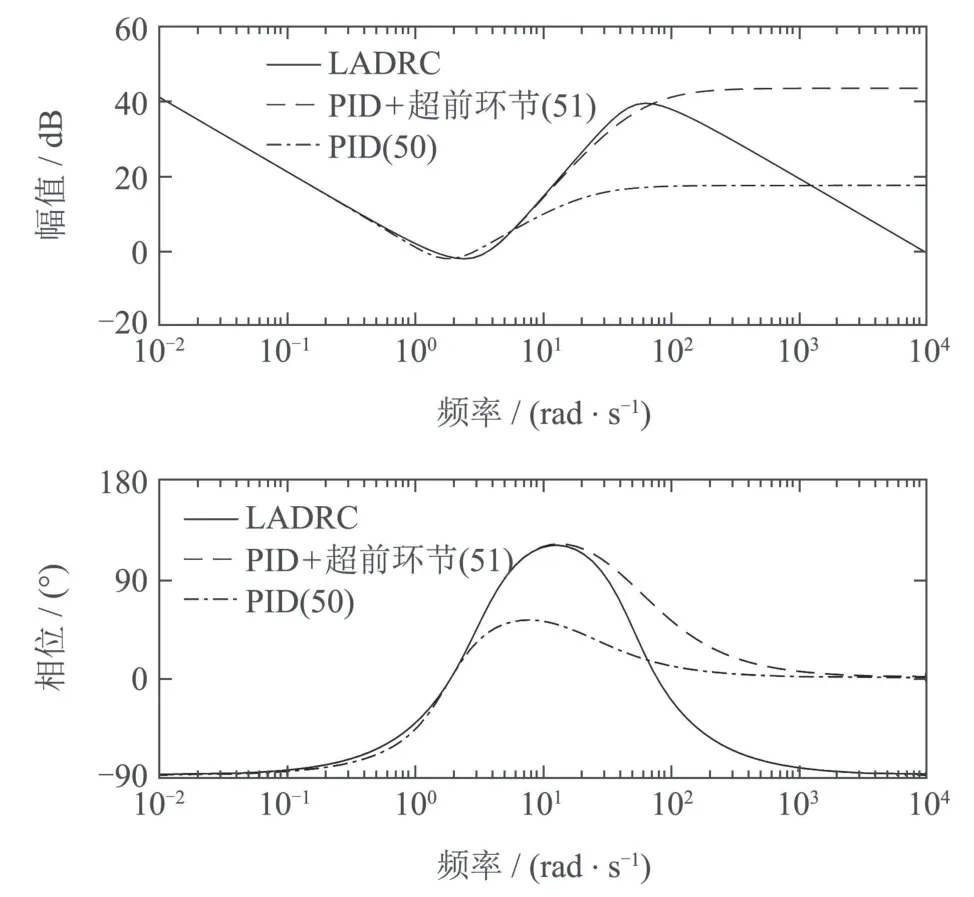
图7 例3系统LADRC和PID的Bode图对比Fig.7 Comparison of the Bode plots of LADRC and PID for Example 3

图8显示的是t=1 s加入ΔPd=0.01的负荷扰动后电力系统的响应.可以看到，由PID+超前环节(51)得到的控制器的抗干扰性能与原3阶LADRC控制器几乎重合.与2阶LADRC情形不同，此时PID控制器(50)的抗扰性能与原3阶LADRC相比，性能有所下降.

图8 例3系统在LADRC及PID下的响应Fig.8 Responses of Example 3 under LADRC and PID

对于高阶LADRC，可以预测用PID控制器逼近后的控制性能会有显著下降，此时有必要采用更高阶的超前环节.例如，对于4阶LADRC，其传递函数可以写成如下带有积分的4阶传递函数形式:

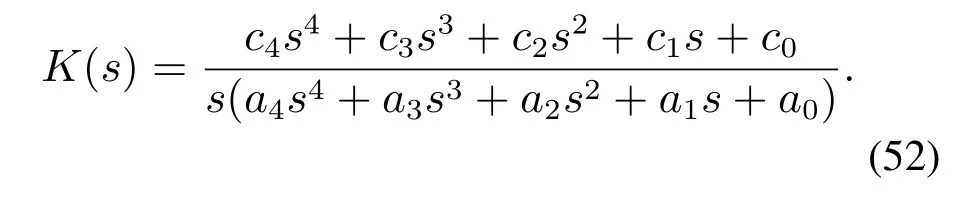
式(52)中分子多项式为4阶，可以分解为(m2s2+m1s+m0)(α2s2+α1s+1)的形式.类似地，式(52)分母多项式也可以分解为s(n2s2+n1s+n0)(β2s2+β1s+1)的形式.忽略n2s2项，可以将式(52)转化为如下形式:

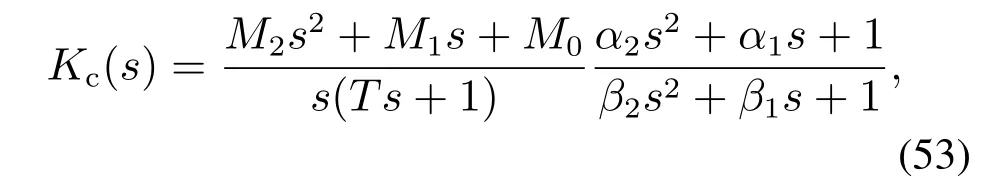
从而利用上节方法可以将式(53)转化为PID+2阶超前环节的形式:

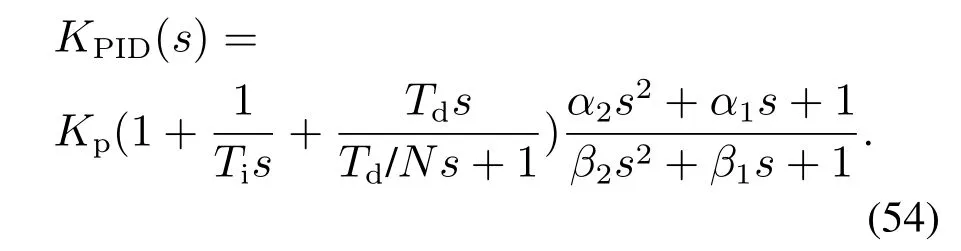
同样地，对式(54)进行通分并化简可得

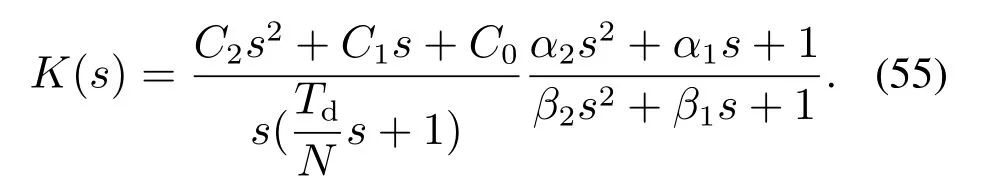
对比式(53)(55)并利用式(34)已有结论，便可推导出式(54)所需参数.

例4考虑文献[21]中针对Two-Mass-Spring系统设计的一个黑箱4阶LADRC，参数为ωc=1，ωo=15，b=1.由LADRC状态空间表达式(5)可以得到该4阶LADRC控制器的反馈环传递函数:

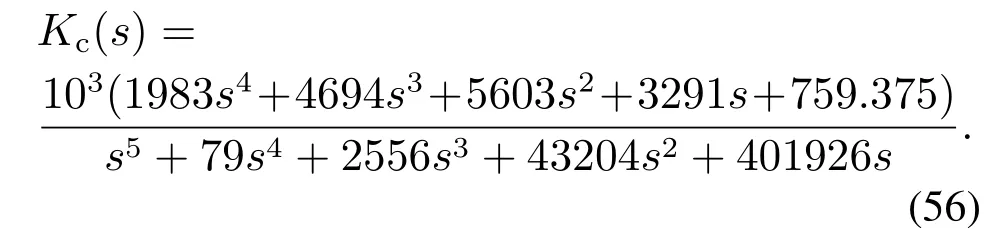
采用频域近似法式(42)-(44)可以将其近似为理想PID控制器，参数为

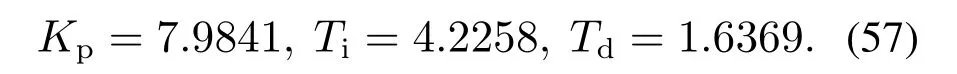
采用PID+2阶超前环节形式(54)，得到参数:

而采用PID+1阶超前环节形式(45)，得到参数:

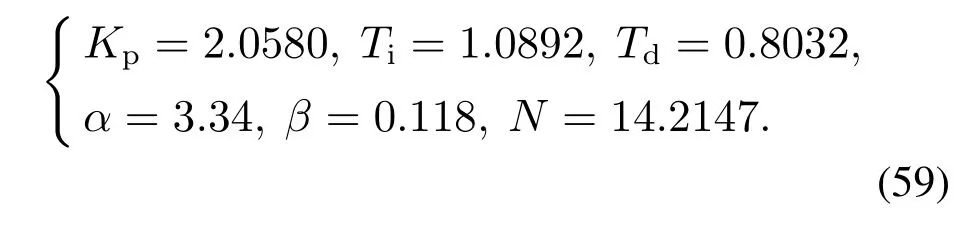
图9给出4阶LADRC，PID(57)，PID+1阶超前环节(59)，以及PID+2阶超前环节(58)的Bode图.可以看到，PID(57)还是PID+1阶超前环节(59)在中频段与原4阶LADRC控制器都存在较大的误差，表现在相位上不能接近原4阶LADRC控制器.而PID+2阶超前环节(58)的相位已经很接近原4阶LADRC，从而在中频与原4阶LADRC更为接近.

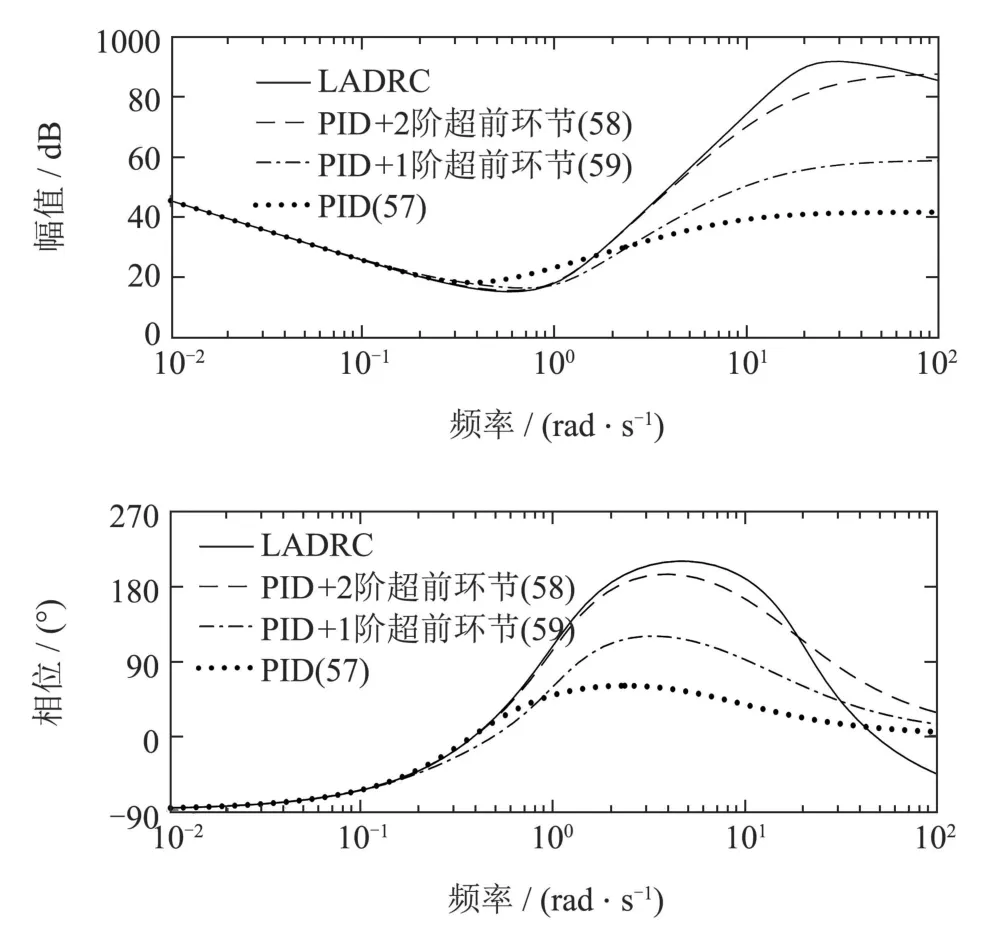
图9 例4系统LADRC和PID的Bode图对比Fig.9 Comparison of the Bode plots of LADRC and PID for Example 4

图10显示的是文献[21]中的对象在单位脉冲扰动后系统的响应.可以看到，由PID+2阶超前环节得到的控制器最终也能够使得系统趋于稳定，但是调节时间较长，动态品质不如原4 阶LADRC.说明用PID去近似该4 阶LADRC 效果并不好，进一步证明了高阶LADRC有很好的控制性能，有更广泛的应用前景.

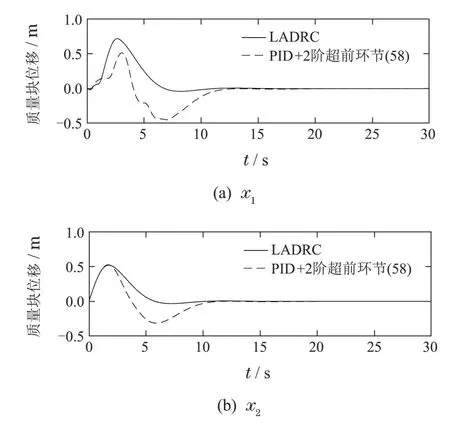
图10 例4系统在LADRC及PID+2阶超前环节(58)下的响应Fig.10 Responses of Example 4 under LADRC and PID+two order lead/lag(58)

在以上实例中分别在输出端加入白噪声扰动，计算方差并进行比较，结果如表1所示.

表1 自抗扰控制以及近似PID方差比较Table 1 Comparison of variance of LADRC and approximation PID

由表1可知，在例1系统的输出端加入白噪声的扰动时，用本文提出的实际PID 的控制效果和2 阶LADRC的控制效果几乎相同;而对于例2系统，PID的效果明显不如LADRC，但本文提出的实际PID还是优于理想PID[9].对于例3系统，由于实际PID+1阶超前环节对3阶LADRC极高的近似程度，实际PID+1阶超前环节对于白噪声的抑制能力也略优于3阶LADRC.

6 结论

本文首先得出了ESO的广义扰动中实际包含有积分项的结论，进一步说明了2阶LADRC和PID结构之间的关系.进而采用实际PID或实际PID+n阶超前环节的策略近似不同阶的LADRC.仿真结果表明，2阶和3阶LADRC采用实际PID和实际PID+超前环节的近似方法就可以取得很好的效果，但对于更高阶的LADRC，本文用实际PID+2 阶超前环节近似4 阶LADRC，在相位上已经非常接近，但在实例中控制效果略逊于4 阶LADRC.因此在实际应用中，高阶LADRC有更好的控制性能，可以弥补PID带来的缺陷，有更广泛的应用前景.