基于衰减因子和动态学习的改进樽海鞘群算法

陈 雷 ，蔺 悦，康志龙

(1.天津大学微电子学院，天津 300072;2.天津商业大学信息工程学院，天津 300134;3.河北工业大学电子信息工程学院，天津300401)

1 引言

樽海鞘群算法(salp swarm algorithm，SSA)[1]是澳大利亚学者Mirjalili在2017年提出的一种新型群智能优化算法，该算法模拟了海洋动物樽海鞘的群体觅食行为，机制简单易懂，操作方便，易于实现，已经成为国内外很多学者的研究热点.目前，该算法已经被应用于光伏系统优化[2-4]、网络系统管理[5]、特征选择[6-7]、图像处理[8-10]和训练神经网络[11]等实际问题中.

SSA相较于其他一些智能优化算法具有一定优势，参数设置简单，收敛速度快，鲁棒性强，处理低维问题优化性能良好.但是SSA也存在迭代后期搜索精度不高，种群多样性较差等缺点，限制了算法的局部开发能力和全局探索能力.为改善其优化性能，许多研究学者提出多种改进算法.从改进参数的角度:Sayed等人[12]将混沌映射引入SSA，用混沌变量代替重要随机参数，加强随机参数的动态特性，提高了SSA的开发和探索能力.Wang等人[13]提出一种基于单纯形法的改进樽海鞘群算法，改变随机策略，增加种群的多样性，加强了算法的局部搜索能力.Qais等人[14]调整领导者趋向食物源的重要参数，并且在跟随者位置更新公式中添加随机参数，帮助领导者更好的趋向最优值，改善了SSA求解精度不足的缺陷.从与其他智能优化算法结合的角度:Ibrahim等人[15]将SSA与粒子群优化算法结合，提高在探索时期的灵活性和多样性，达到了更高的寻优效率.Khamees等人[16]将SSA与模拟退火算法结合，在解决多目标优化问题上表现出色.

以上改进算法均从不同角度增强了SSA算法的寻优性能.但在实际问题中，往往是高维单峰和高维多峰的复杂问题.对于解决这类复杂的优化问题，SSA的求解精度和寻优效率仍需进一步提高.针对上述存在的问题，本文提出一种基于衰减因子和动态学习的改进樽海鞘群算法(salp swarm algorithm based on reduction factor and dynamic learning，RDSSA)，在领导者位置更新阶段添加衰减因子，提高算法在迭代后期的局部开发能力;在跟随者位置更新阶段引入动态学习策略，提高算法的全局探索能力，解决了算法在高维多峰优化问题上求解精度不高，寻优效率低的问题.

通过对16个测试函数进行实验，并与其他改进樽海鞘群算法及其他智能优化算法比较，验证RDSSA的优化性能.

2 樽海鞘群算法

SSA建立了一种用于求解优化问题的樽海鞘链模型，将樽海鞘群分为两类:领导者和跟随者，领导者是处在链的前面起带领作用的个体，跟随者直接或间接地相互追随.樽海鞘的位置在D维搜索空间中定义，食物源F作为樽海鞘群的觅食目标.

领导者的位置更新公式如下:

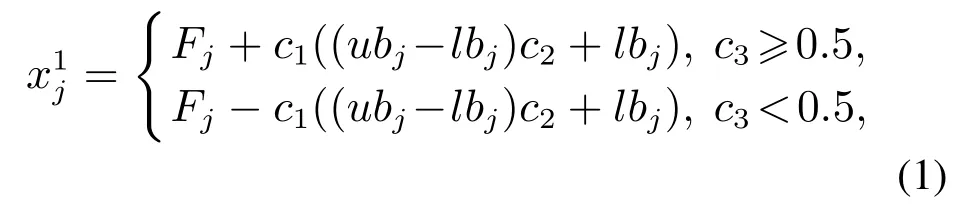
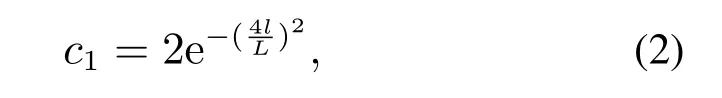
跟随者的位置更新公式如下:

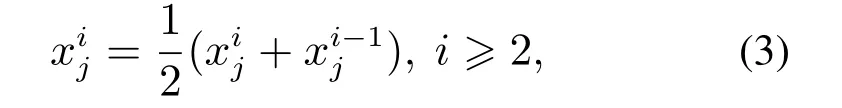
SSA采用优胜劣汰策略，通过计算所有个体的适应值，比较当前迭代次数的适应值与先前最优适应值，不断接近食物源位置.由此可以模拟樽海鞘群的觅食行为，解决最优化问题.

3 基于衰减因子和动态学习的改进樽海鞘群算法

通过研究SSA的原理发现，由于位置更新搜索范围无约束，且精英个体的影响权重小，导致SSA在迭代后期不能进行很精确的搜索，跟随者不能很好的协助个体位置更新.因此，本文的改进思路从两个方面考虑:针对SSA在领导者更新阶段搜索范围不受限的问题，添加衰减因子，增强迭代后期的局部开发能力;针对跟随者位置更新的局限性，引入动态学习策略，提高全局探索能力.

3.1 添加衰减因子的樽海鞘群算法

基本SSA在领导者位置更新阶段，个体在食物源附近移动，搜索范围不受限制，使得收敛后期个体不能在极值点进行精确搜索，还有可能跳出极值点.为了改善这一问题，本文提出将衰减因子引入SSA，得到添加衰减因子的樽海鞘群算法(reduction factor salp swarm algorithm，RSSA)，使得领导者位置更新范围随着迭代次数的增加而逐渐减小，收敛前期避免陷入局部极值，收敛后期越来越逼近最优值，达到更高的求解精度.

添加衰减因子的领导者位置更新公式(4)如下:

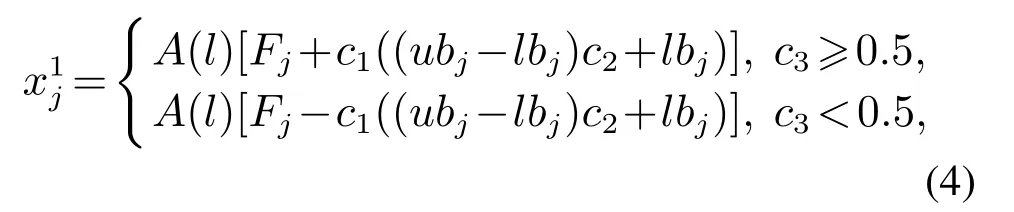
其中控制搜索范围的衰减因子A(l)是一个非线性递减函数，定义如下:

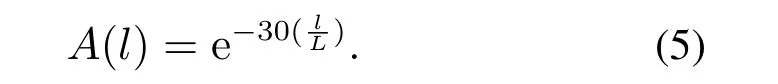
收敛前期，搜索范围不受限，个体可以充分在全局移动，充分发挥算法的全局搜索能力，避免陷入局部极值;收敛后期，随着个体越来越逼近最优值，搜索范围也逐渐减小，个体在限制范围内进行精确搜索，增强局部搜索能力，以达到更高的求解精度.

3.2 引入动态学习的樽海鞘群算法

基本SSA算法没有参数影响跟随者的位置更新，跟随者的移动由个体自身位置和前一个个体位置综合决定，精英个体的影响权重小，使得跟随者对领导者的协助作用很小.为了增强精英个体的影响权重，本文将动态学习策略引入SSA，得到引入动态学习的樽海鞘群算法(dynamic learning salp swarm algorithm，DSSA)，先比较的适应值，在适应值较大的位置(即离最优值距离较远的位置)上添加削弱因子k，以削弱较差位置个体的影响权重，增强较优位置个体的影响权重.

引入动态学习策略的跟随者位置更新公式如下:

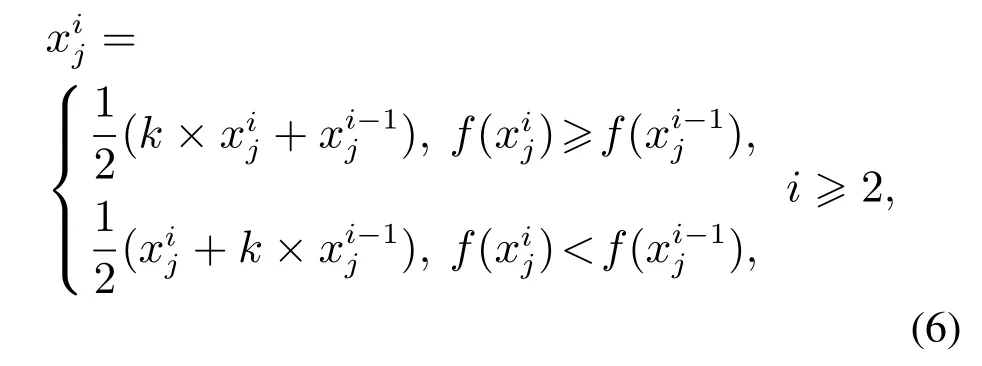
在收敛过程中，精英个体能更好的发挥协助作用，帮助领导者做决策，不断向食物源逼近，提高寻优效率.

3.3 RDSSA的实现流程

将RSSA和DSSA结合，同时改变领导者和跟随者的位置更新公式，可以得到新的优化算法RDSSA，提高领导者局部开发能力，增强跟随者的协助作用，以提高收敛速度，获得更好的优化效果.RDSSA的实现流程如下所示.

Step 1设定种群规模N、迭代次数Iteration、维数D和上、下边界;

Step 2初始化樽海鞘群个体的位置，并计算各个体的适应值Fitness，将最小适应值个体的位置确定为食物源位置FoodPosition;

Step 3生成衰减因子A(l)，根据式(4)更新领导者位置;

Step 4生成随机数k，根据式(6)更新跟随者位置;

Step 5计算更新位置后的个体适应值，若小于当前FoodPosition，则更新FoodPosition;

Step 6判断当前迭代次数是否达到预设迭代次数，若已达到，结束迭代，否则返回执行Step 3;

Step 7输出FoodPosition位置及该位置上的适应值Fitness.

RDSSA的伪代码如下所示:

4 测试实验分析

4.1 实验设计

为了验证本文提出的RSSA，DSSA和RDSSA的性能，实验选取16个典型全局优化测试函数进行实验.测试函数的形式、搜索范围、理论极值和目标收敛精度如表1所示，其中f1～f8为单峰函数，f9～f16为多峰函数.本文实验分为3个部分:1)与基本SSA比较，固定迭代次数，观察收敛速度和收敛精度;2)与基本SSA比较，固定目标收敛精度，观察达到目标收敛精度所需的迭代次数;3)与其他算法比较，固定迭代次数，观察收敛速度和收敛精度.

实验硬件配置为Intel(R)Core(TM)i5-3210M，CPU 2.50 GHz，RAM 4.00 GB，Windows 64 位操作系统，算法调试运行基于MATLAB 2014a.为了遵循实验公平性原则，实验基本参数保持一致:种群数量N设为50，函数维数D分别设为30，45和60，迭代次数Iteration设为500，每次实验结果为独立运行30次的平均值.

4.2 实验结果及分析

4.2.1 固定迭代次数下的收敛精度

固定迭代次数的实验结果如图1所示，显示了SSA，RSSA，DSSA和RDSSA4种算法对以上16个测试函数的收敛曲线.为了便于观察，将收敛曲线的纵轴刻度设置为以10为底的指数形式.

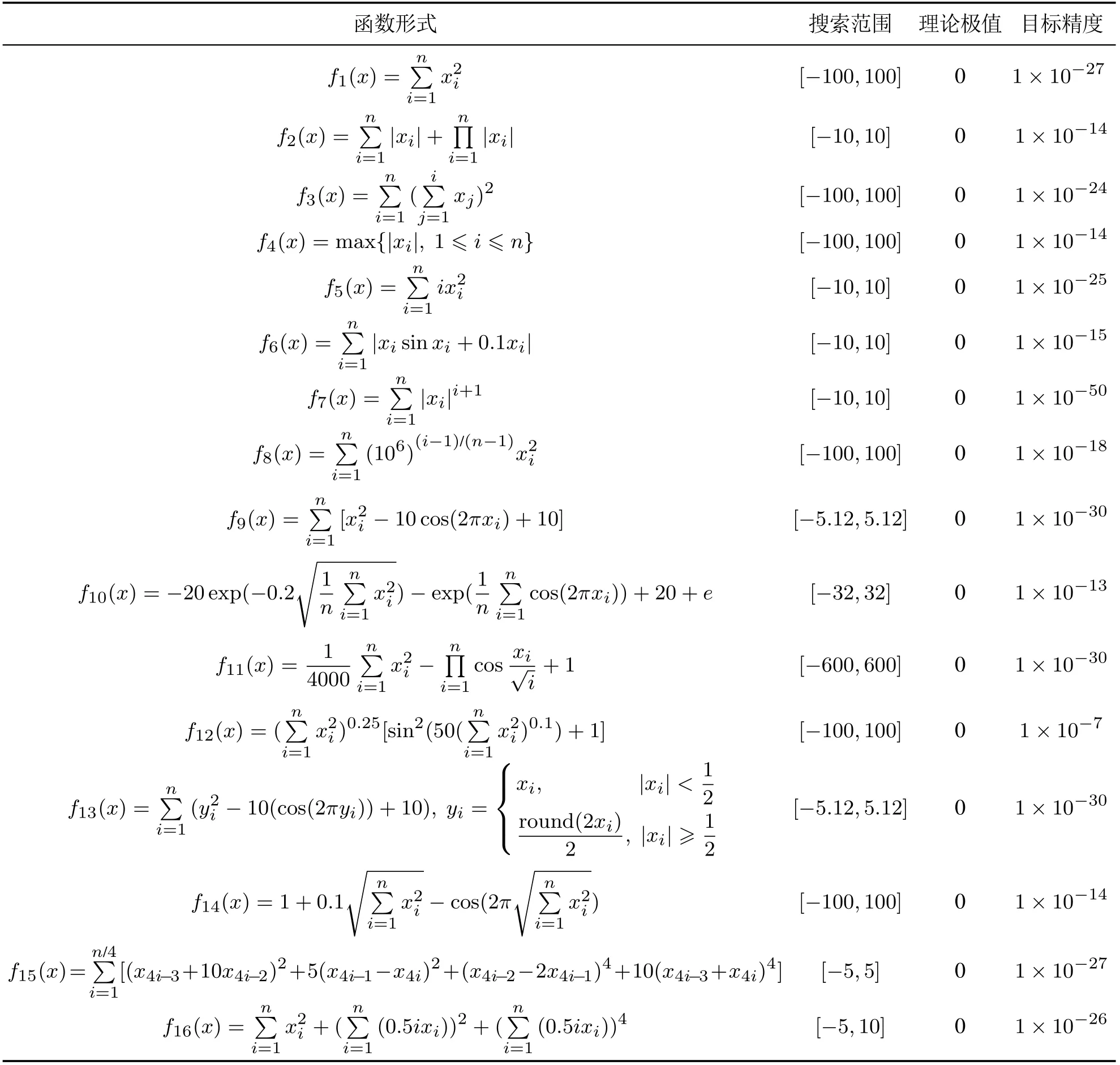
表1 典型测试函数Table 1 Benchmark test functions

由图1可以看出，在经过500次迭代之后，RSSA，DSSA和RDSSA都能接近测试函数的理论极值，且收敛速度和收敛精度都比传统SSA要高.RSSA在200次迭代之后，收敛速度明显变快，尤其是对于多峰测试函数，在避免陷入局部极值、后期迭代速度方面相较于SSA优势明显.DSSA在前期迭代速度快，后期迭代优化稳定性强，尤其在测试函数f7，f11和f13上，获得明显优于SSA的准确性和高效性.综合来看，RDSSA具有最快的收敛速度和最精确的收敛精度，说明RDSSA具有更好的寻优性能.

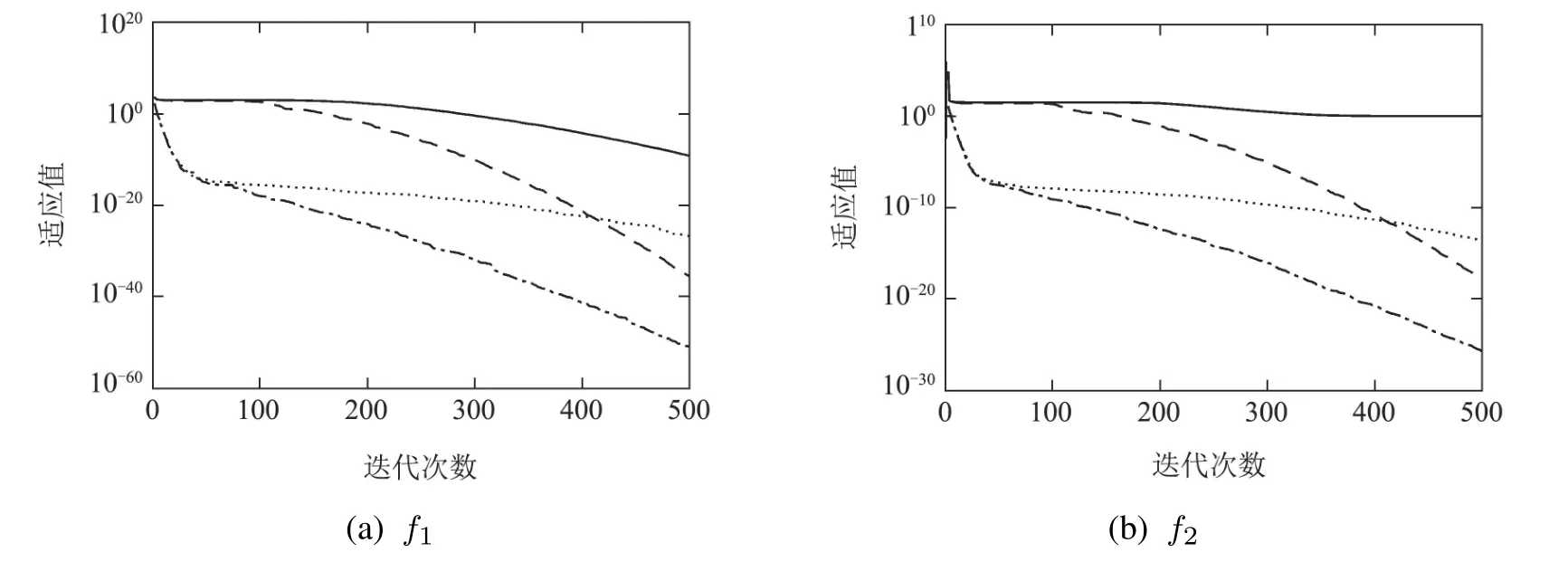
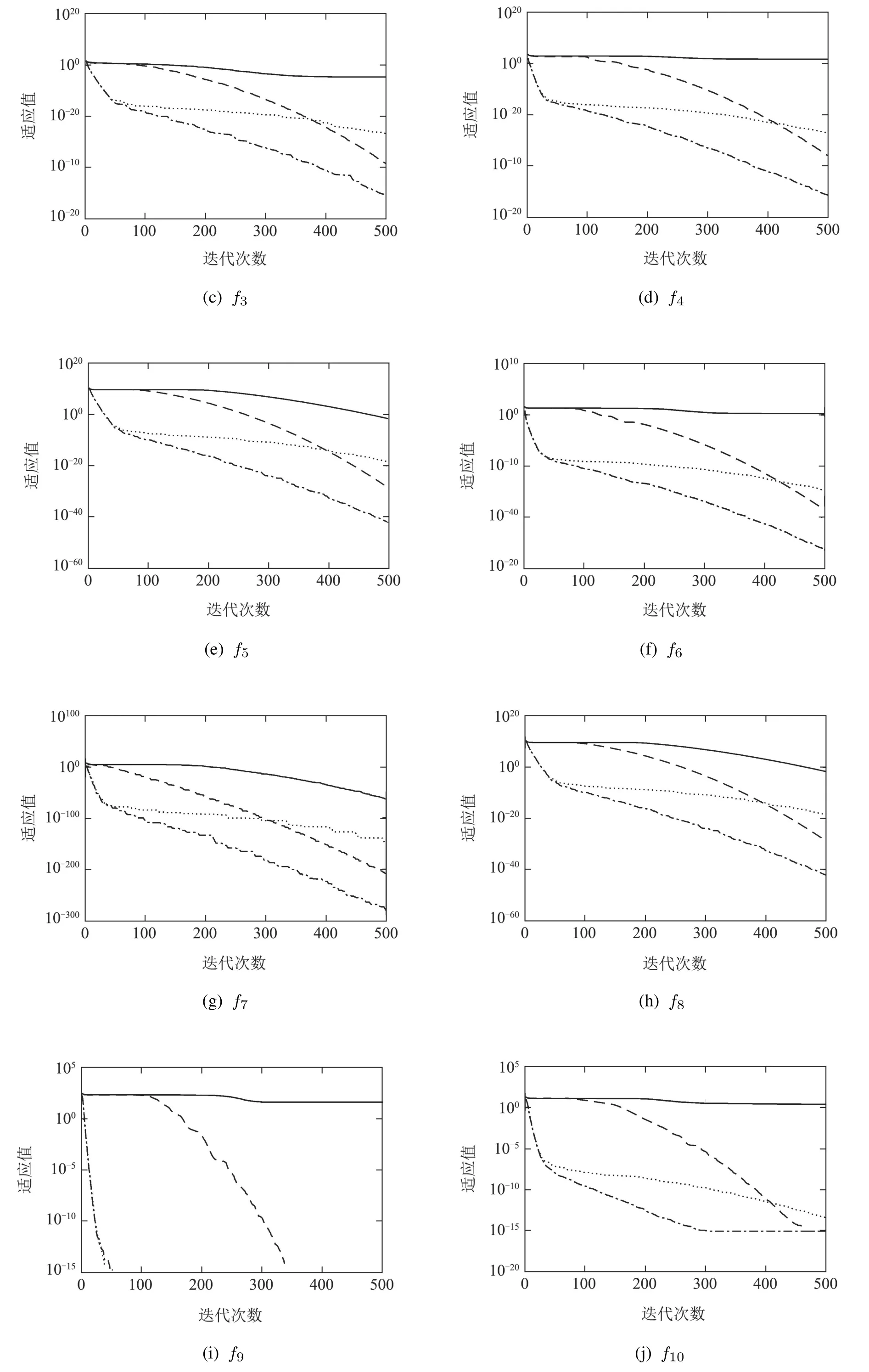
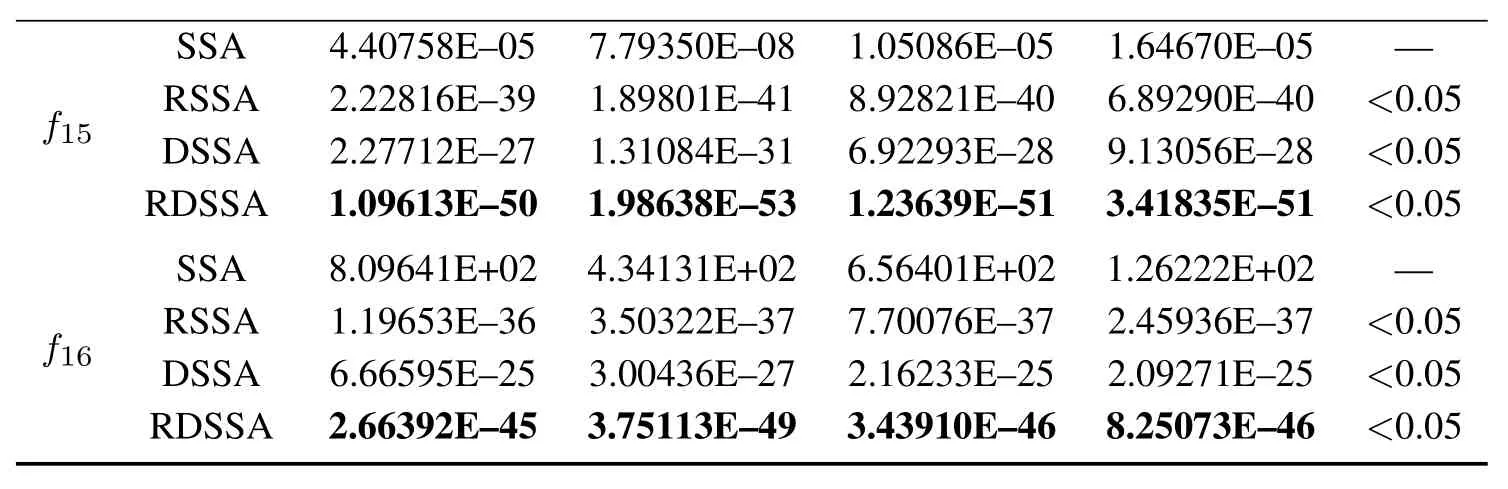
表2显示了4种算法对16个测试函数在固定迭代次数下的收敛精度结果比较.计算得到适应值的最大值(Max)、最小值(Min)、平均值(Ave)和标准差(Std)，分别表示算法所能达到的求解精确度的最差值、最优值、平均值和求解稳定性.由于本实验所用的计算机能表示的最小浮点数为2.2251E-308，当收敛精度达到E-308量级时，结果显示为数值0.p-value表示SSA分别与RSSA，DSSA和RDSSA的Wilcoxon秩和检验结果，体现算法间的显著性差异，当p-value的值小于0.05时，说明改进算法效果明显优于SSA.

通过分析表2数据，RSSA与DSSA的收敛精度相比较于SSA都有改善，除了f10，RDSSA的优化效果基本与RSSA持平，其余测试函数RDSSA的收敛精度最高.

对于多峰测试函数f9，f11，f13和f14，RDSSA的收敛精度远超SSA.p-value值基本都小于0.05，说明RDSSA比SSA有明显优越性.

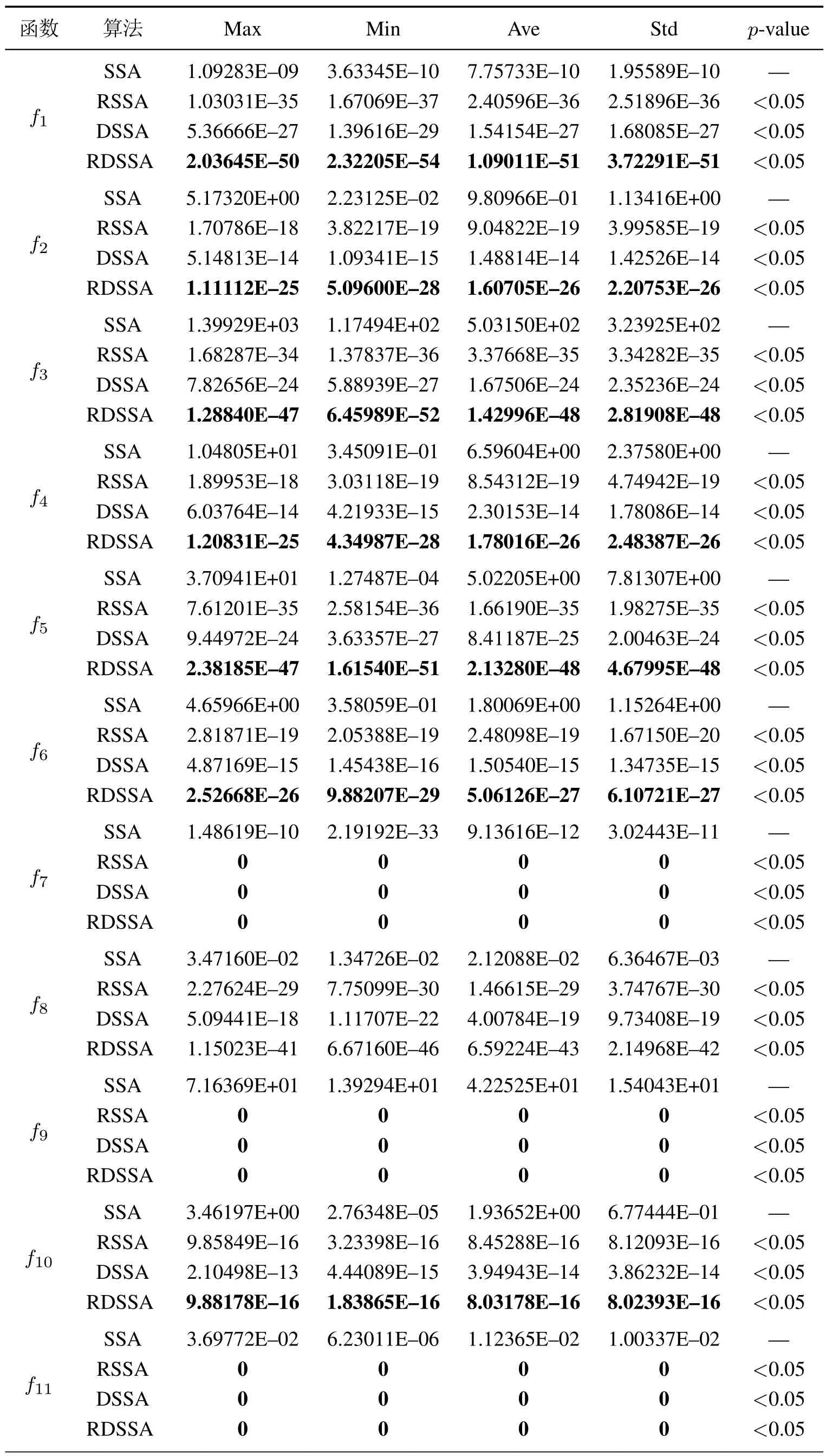
表2 固定迭代次数下的收敛精度(30维)Table 2 Convergence accuracy in fixed iteration(30 dimensions)

为了进一步验证RDSSA在解决复杂的高维问题的优化性能，本文增加了45维和60维的测试函数的实验，观察固定迭代次数下的收敛精度.实验结果如表3和表4所示.通过分析表3和表4的数据，RSSA，DSSA 和RDSSA在45 维和60 维的收敛精度均高于SSA，充分验证了RDSSA解决高维问题的优势.

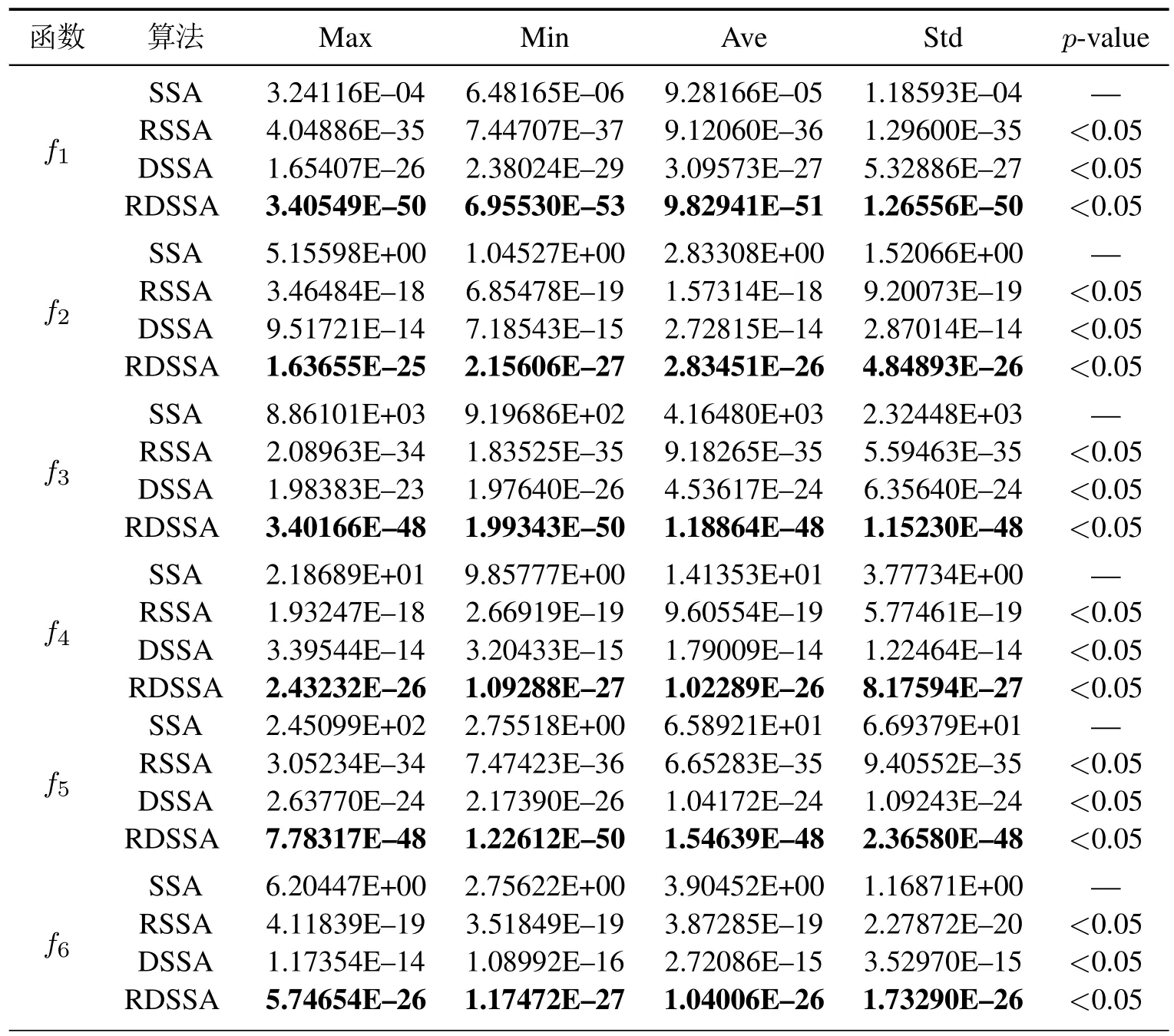
表3 固定迭代次数下的收敛精度(45维)Table 3 Convergence accuracy in fixed iteration(45 dimensions)

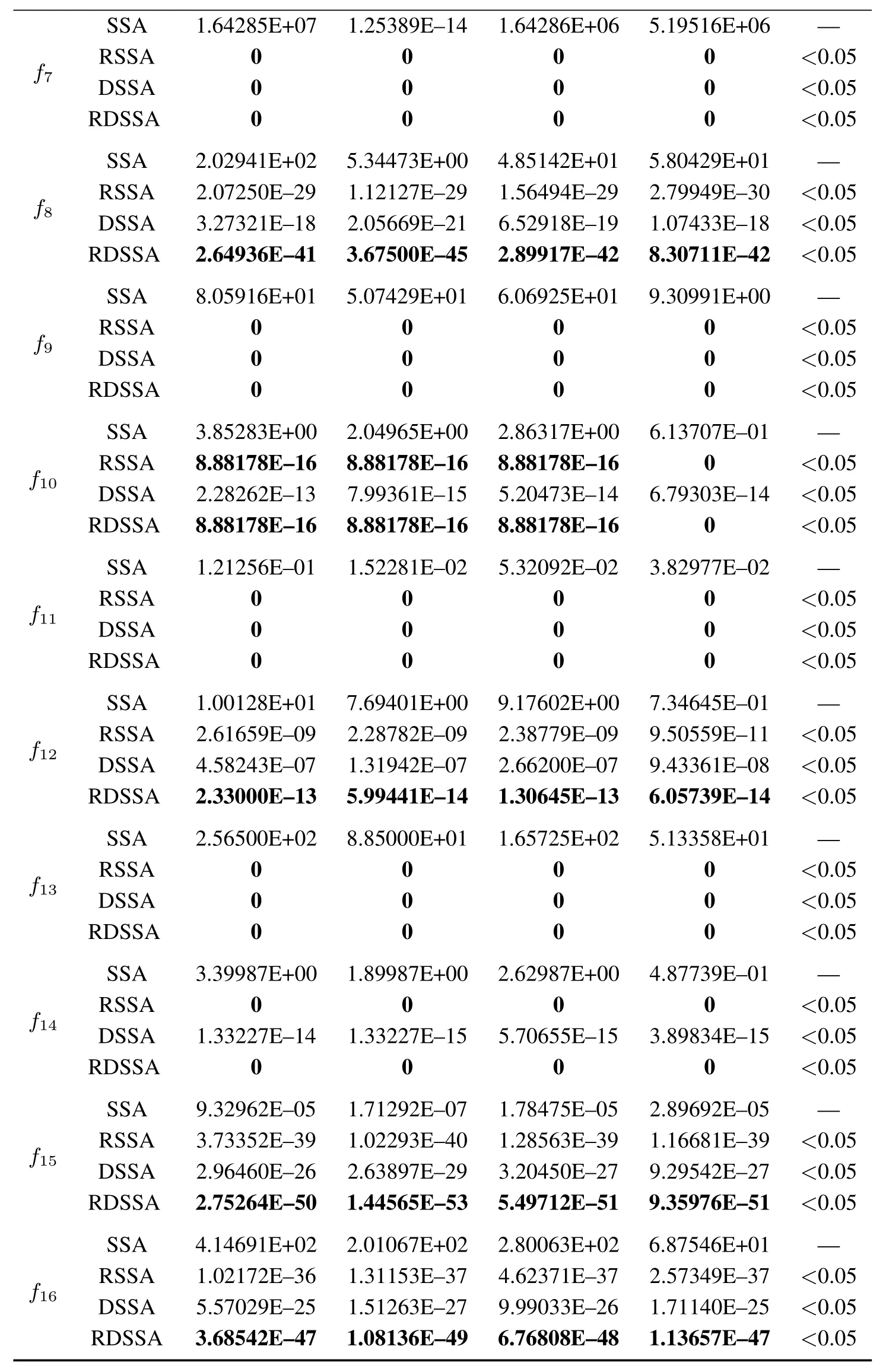
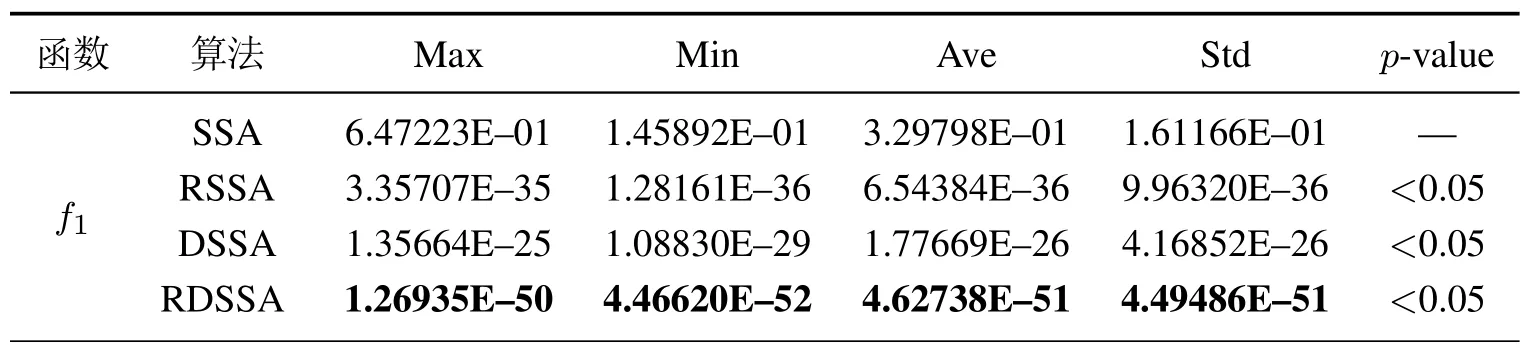
表4 固定迭代次数下的收敛精度(60维)Table 4 Convergence accuracy in fixed iteration(60 dimensions)

4.2.2 固定目标精度下的迭代次数

固定目标精度下的实验结果如表5所示.

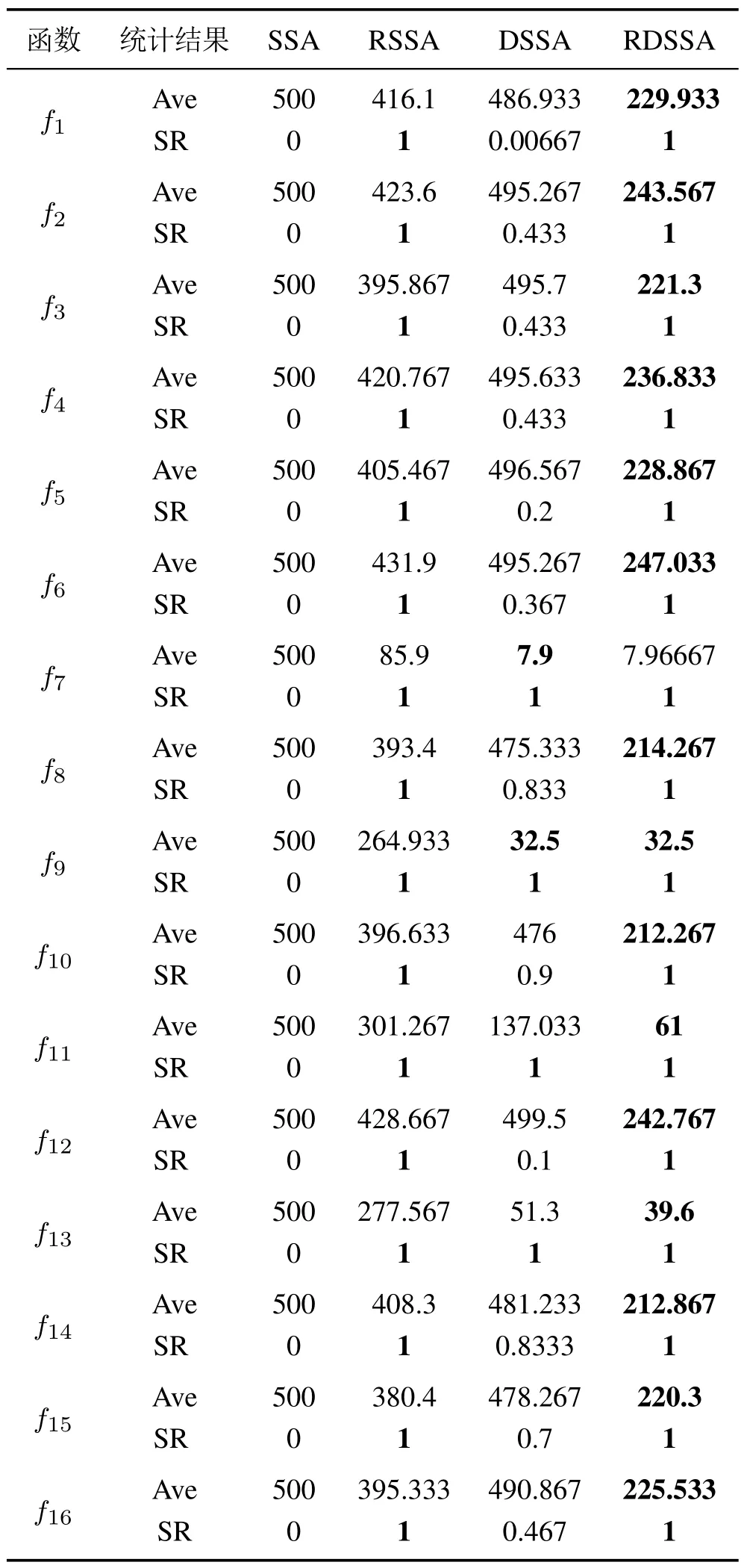
表5 固定目标精度下的实验结果Table 5 Test results in fixed precision

由于测试函数复杂度不同，设置的目标精度也不同，具体数值设置如表1所示，函数维数D为30.表5中Ave表示算法30次独立运行能够达到目标精度的平均迭代次数，如果某次独立运行500次迭代后仍未达到目标精度，则取该次迭代次数为500.SR表示算法能在500次迭代内达到目标精度的成功率.2 通过表5数据可知，SSA的成功率基本为0，说明其优化能力有待提高.对于测试函数f9～f11和f13～f15，DSSA的成功率均高于70%，说明DSSA对于多峰优化问题的寻优性能更好.RSSA的成功率均为100%，说明RSSA具有较快的收敛速度.RDSSA不仅成功率均为100%，且平均迭代次数远远小于RSSA，均未超过250，说明RDSSA具有更快的收敛速度和更好的优化效果.

4.2.3 与其他算法比较

为了进一步验证RDSSA 的优化性能，将其与增强的樽海鞘群算法(enhanced salp swarm algorithm，ESSA)[14]、混沌的樽海鞘群算法(chaotic salp swarm algorithm，CSSA)[12]、飞蛾火焰算法(moth-flame optimization algorithm，MFO)[17]、多重宇宙优化(multiverse optimizer，MVO)[18]算法、神经网络算法(neural network algorithm，NNA)[19]、粒子群优化(particle swarm optimization，PSO)[20]算法、人工蜂群(artificial bee colony，ABC)[21]算法和差分进化(differential evolution，DE)[22]算法进行比较.其中，ESSA 和CSSA是SSA的改进算法，MFO，MVO和NNA是近3年被提出的新颖的全局优化算法，PSO，ABC和DE是效果较好的经典智能优化算法.为了遵循实验的公平性原则，种群数量、函数维数、迭代次数和独立运行次数等基本实验参数与文献[12]保持一致，文献[22]中的参数F设置为[0.2，0.9]的随机数，CR设置为0.2，其余文献中的参数均与原文献保持一致.表6中CSSA数据来自文献[12].实验结果如表6和图2所示.

表6中Ave和Std分别代表计算得到的适应值的平均值和方差，是评判算法收敛精度和稳定性的指标.由表6 可以看出，除了f9～f11和f13，RDSSA 和ESSA的收敛精度和收敛稳定性相当，在其余测试函数上，RDSSA都表现出了比其他算法更优秀的收敛能力，特别是f7和f14，RDSSA的收敛精度和收敛稳定性远超于其他算法.

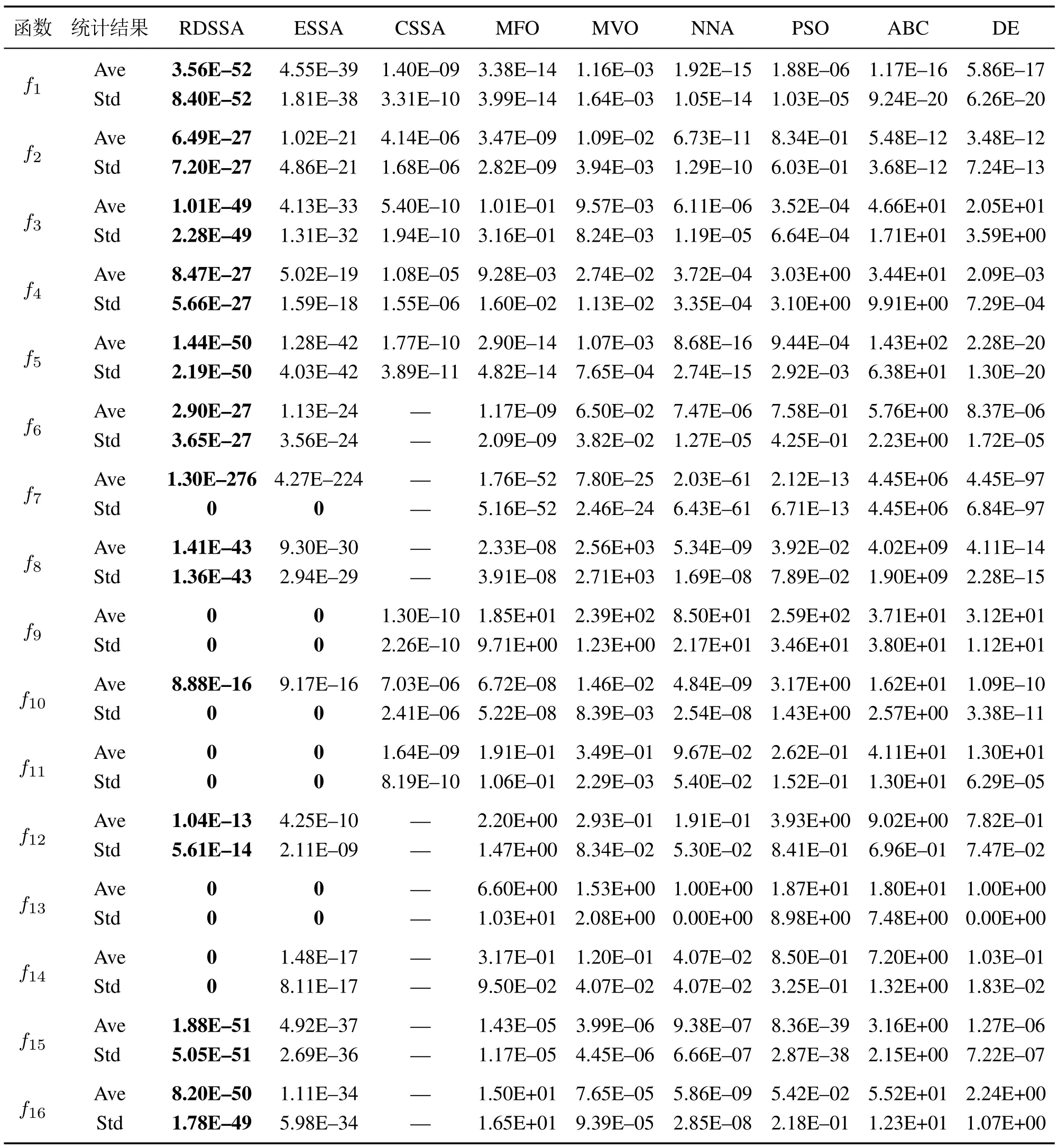
表6 与其他算法的收敛精度比较Table 6 Comparison of convergence accuracy with other algorithms

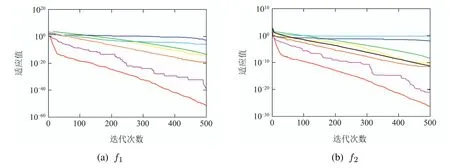
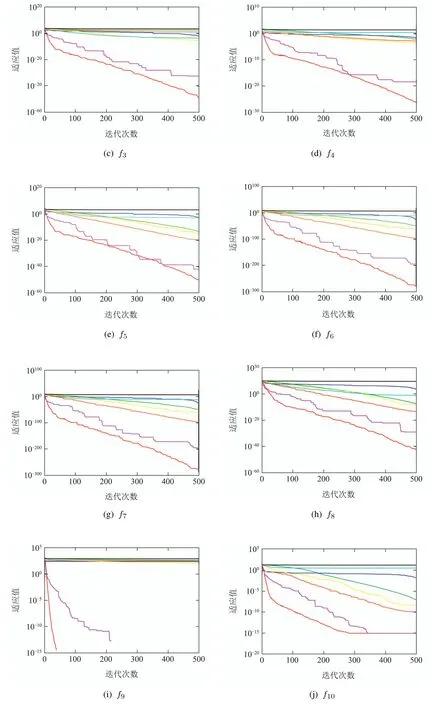
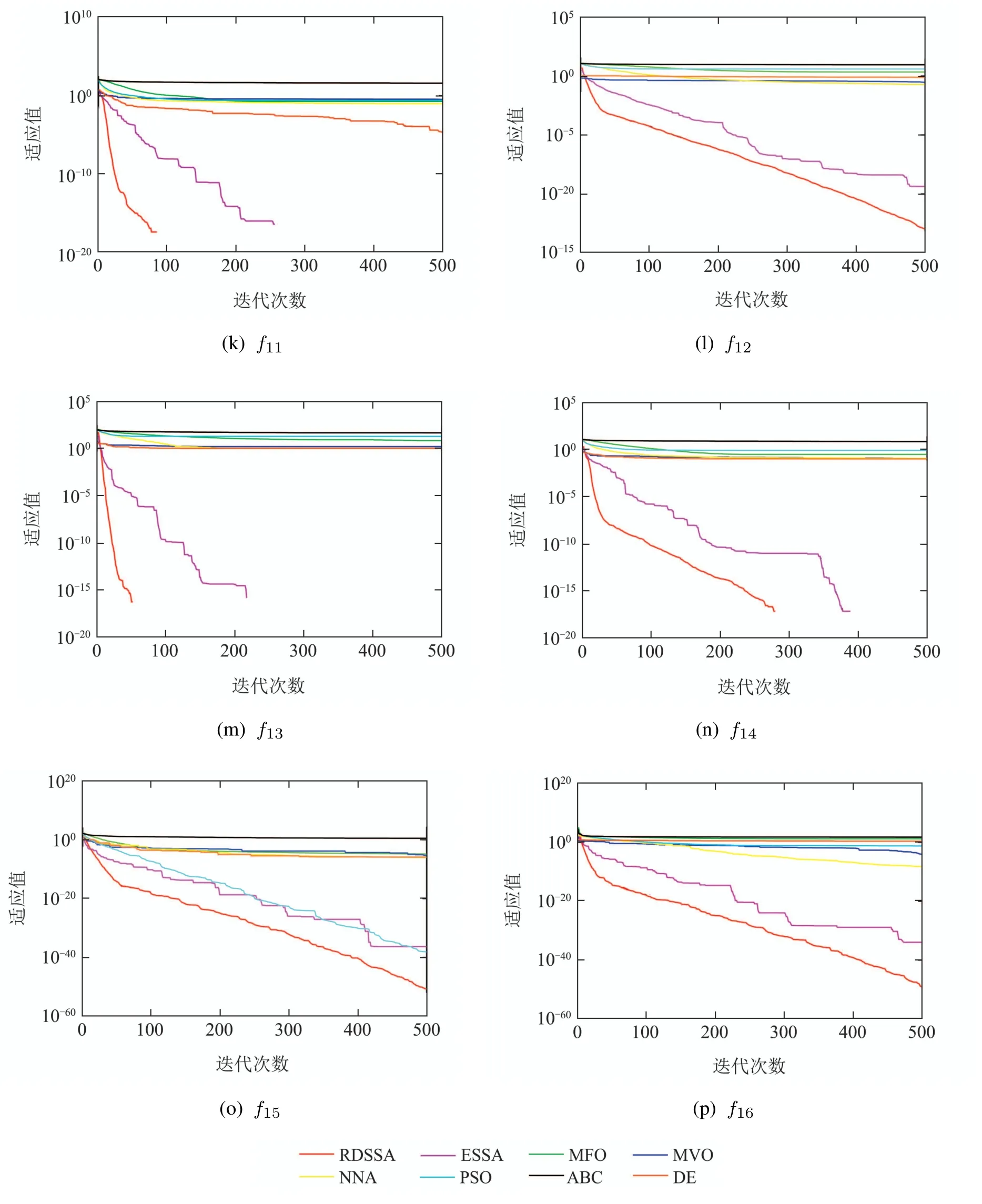
图2 与其他算法收敛曲线比较Fig.2 Comparison of convergence curves with other algorithms

图2显示了几种算法的收敛曲线比较，可以看出对于单峰函数，RDSSA在100次迭代前速度很快，之后以既快又稳定的速度收敛，最终达到最好的优化效果，ESSA其次，也能得到较好的收敛精度，其余算法收敛速度较慢，优化效果不佳.对于多峰函数，特别是f9，f11，f13和f14，RDSSA和ESSA的收敛速度优势明显，RDSSA的优化效果最好.综合来看，RDSSA相比于其他智能优化算法，具有较快的寻优速度和较好的寻优性能.

5 结论

本文提出了一种基于衰减因子和动态学习的改进樽海鞘群算法，通过添加衰减因子，灵活的控制搜索范围大小，加快了算法收敛速度，通过引入动态学习策略，加强了跟随者对于寻优的协助作用，达到了更高的收敛精度，改善了SSA的优化性能.实验结果表明，RDSSA相较于基本SSA、其他改进SSA和其他智能优化算法，在收敛精度和收敛速度方面都有较大提升，在最优化问题领域有着广泛的应用前景.