基于核心素养的函数模型思想方法在中考中的应用

广省省梅州市梅县外国语学校(514799) 叶峰华

1 初中阶段课程标准对函数模型思想方法的相关要求

《义务教育数学课程标准(2011 版)》[1](以下简称“课程标准”)中明确提出“模型思想的建立是学生体会和理解数学与外部世界联系的基本途径”,并诠释道“在呈现作为知识与技能的数学结果的同时,重视学生已有的经验,使学生体验从实际背景中抽象出数学问题、构建数学模型、寻求结果、解决问题的过程.”

课程标准明确了“函数模型思想方法”是重要的数学模型思想方法之一,其在数学核心素养中居于重要地位[2].同时,课程标准也强调了“当代数学教育应更加注重培养学生数学能力,发展学生数学思维的特点.”由此可见,在当前中考中,必定会更加重视学生函数知识应用能力的考查,具体体现为:题材贴近学生生活实际,以函数模型为考查目标的应用题型,必将成为考查的热点之一.因此,在初中阶段的数学教学中渗透数学建模思想,对初中阶段出现的函数模型进行梳理总结,对提高学生函数知识应用能力和解题能力是很有帮助的[3].

2 函数模型思想方法在中考解题中的应用

初中阶段出现的函数模型主要有以下三种:一次函数模型、反比例函数模型、二次函数模型.

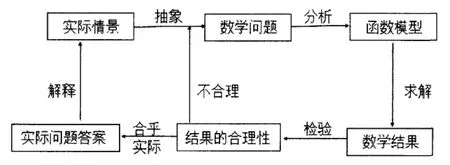
运用函数知识解决实际问题的步骤可用上面的流程图来体现[4]:

2.1 一次函数模型

一次函数模型属于“函数模型”领域中较为基础的模型,与该函数模型相关的题型,往往通过设置与投入产出、工作效率、销售等相关情境,再结合一次函数的性质,特别是其单调性进行考查.另外,一次函数模型的应用题往往会涉及不等式的运算.

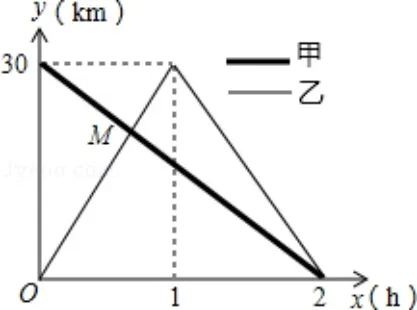
例1(2013• 南宁) 在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人离B地的距离y(km)与行驶时x(h)之间的函数图象,根据图象解答以下问题:

(1)写出A、B两地之间的距离;

(2)求出点M的坐标,并解释该点坐标所表示的实际意义;

(3)若两人之间保持的距离不超过3km 时,能够用无线对讲机保持联系,请直接写出甲、乙两人能够用无线对讲机保持联系时x的取值范围.

分析(1)x=0 时甲的值即为A,B两地的距离;

(2)根据图象求出对应直线的解析式,通过联立二元一次方程组求出点M的坐标,并结合题意说明其实际意义;

(3)分相遇前和相遇后两种情况求出x的值,再求出最后两人都到达B地前两人相距3 千米的时间,然后写出x取值范围即可.

解答(1)x=0 时,甲距离B地30km,所以,A、B两地的距离为30km.

(2)设甲直线解析式为y1=k1x+b1(k1≠0),乙从B地到A地过程中(0x1),其直线解析式为y2=k2x,(k2≠0).

将(2,0),(0,30) 代入y1=k1x+b1(k1≠0) 得:解得:∴y1=−15x+30,将(1,30)代入y2=k2x得:30=k2×1,解得:k2=30,∴y2=30x,联立解得:所

以,点M的坐标为,表示小时后两车相遇,此时距离B地20km.

(3)由(2)知v甲=30km/h,v乙=15km/h,设x小时后,甲、乙两人相距3km.

①若是相遇前,则15x+30x=30−3,解得:,

②若是相遇后,则15x+30x=30+3,解得:,

③若是到达B地前,则15x−30(x−1)=3,解得:,所以,当或时,甲、乙两人能够用无线对讲机保持联系.

评价本题考查了一次函数模型的应用.解题过程中,需充分发掘题目信息,利用路程、速度、时间三者之间的等量关系,列出方程.解答此题的难点在于,第(3)问要进行分情况讨论,分类过程中思维要严谨,做到不重不漏.

2.2 反比例函数模型

反比例函数模型是初中阶段的一种重要函数模型,囿于反比例函数性质较为简单,因此反比例函数模型考查较少.在解题过程中主要利用两个变量之间的相互关系进行解答,涉及的应用背景有浓度、经济问题等.

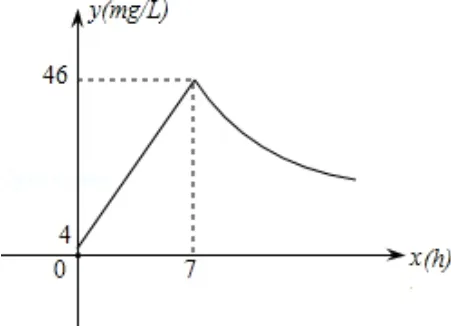
例2(2010•达州)近年来,我国煤矿安全事故频频发生,其中危害最大的是瓦斯,其主要成分是CO.在一次矿难事件的调查中发现:从零时起,井内空气中CO的浓度达到4mg/L,此后浓度呈直线型增加,在第7 小时达到最高值46mg/L,发生爆炸;爆炸后,空气中的CO 浓度与时间成反比例关系.如图所示,根据题中相关信息回答下列问题:

(1)求爆炸前后空气中CO 浓度y与时间x的函数关系式,并写出相应的自变量取值范围;

(2)当空气中的CO 浓度达到34mg/L 时,井下3km 的矿工接到自动报警信号,这时他们至少要以多少km/h 的速度撤离才能在爆炸前逃生?

(3)矿工只有在空气中的CO 浓度降到4mg/L 及以下时,才能回到矿井开展生产自救,求矿工至少在爆炸后多少小时才能够下井?

分析(1)根据图象可以设当0x7 时函数关系式为:y=k1x+b(k1≠0),再由图象经过点(0,4),(7,46)求出函数解析式为:y=6x+4,从而求得自变量x的取值范围.再由图象知,当x7 时,函数解析式为:其过点(7,46),求出k2=322,再由函数解析式求得自变量x的取值范围.

(2)结合以上关系式,当y=34 时,由y=6x+4 得x=5,从而求出撤离的最长时间,再由求出最小速度.

解答(1)因为爆炸前浓度呈直线型增加,所以可设y与x的函数关系式为y=k1x+b(k1≠0),由图象知y=k1x+b(k1≠0)过点(0,4),(7,46),则有:解得:则y=6x+4,0x7.

∵爆炸后浓度成反比例下降,∴可设y与x的函数关系式为由图象知过点(7,46),∴,∴k2=322,∴.

(2)当y=34 时,由y=6x+4 得,6x+4=34,解得:x=5,∴撤离的最长时间为7−5=2(小时).∴撤离的最小速度为3÷2=1.5(km/h).

(3)当y=4 时,由得,x=80.5,80.5−7=73.5(小时).∴矿工至少在爆炸后73.5 小时才能下井.

评价解答该题,首先要根据图像信息,确定函数类型,再用待定系数法求出对应的函数解析式,然后根据题目信息求得对应的函数值,从而解得结果.

2.3 二次函数模型

二次函数模型是初中乃至整个中学阶段最重要的函数模型之一,因二次函数性质丰富,所以其有着广泛的应用,应用题背景涉及经济、工效,面积问题等等,一般会结合应用情景,考查二次函数最值、单调性等性质.

例3(2015•梅州)九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如下表:

售价(元/件)100 110 120 130···月销量(件)200 180 160 140···

已知该运动服的进价为每件60 元,设售价为x元.

(1)请用含x的式子表示:①销售该运动服每件的利润是____元②月销量是____件;(直接写出结果)

(2)设销售该运动服的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少?

分析(1)售价x减去进价60 即为利润;观察表格,根据售价与月销量相互关系可知,它们之间为一次函数关系.所以设销量为z件,则z与x的关系设为:z=kx+b,将给出的数据中任意两组代入关系式中得:解得:所以销售量为:(−2x+400)件.

(2)用销量乘以每件的利润即为每月的利润,再将得出的二次函数化为顶点式,即可得出本月的最大利润及其所对应的售价.

解答(1)①(x−60); ②(−2x+400).

(2)由题意可得该运动服的月利润y为:y=(x−60)(−2x+400)=−2x2+ 520x−24000=−2(x−130)2+ 9800.因为y=−2(x−130)2+ 9800 图像是开口向下的抛物线,所以当x=130 时,y取得最大值,ymax=−2×(130−130)2+9800.故售价为每件130 元时,当月利润最大,最大利润为9800 元.

评价本题综合考查了一次函数和二次函数的综合应用,第(1)问和第(2)问具有承接关系,做题时必须细心,一步一个脚印避免犯错.另外,要熟悉“总利润=单个利润×销量”这个公式,从而得到月利润的正确表达式,再利用二次函数相关知识求得最大利润.

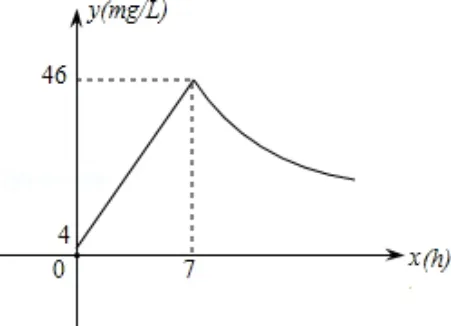
例4(2011•四调武汉)杰瑞公司成立之初投资1500 万元购买新生产线生产新产品,此外,生产每件该产品还需要成本60 元.按规定,该产品售价不得低于100 元/件且不得超过180 元/件,该产品销售量y(万件)与产品售价x(元)之间的函数关系如图所示.

(1)求y与x之间的函数关系式,并写出x的取值范围;

(2)第一年公司是盈利还是亏损?求出当盈利最大或者亏损最小时的产品售价;

(3)在(2)的前提下,即在第一年盈利最大或者亏损最小时,第二年公司重新确定产品售价,能否使两年共盈利达1340 万元?若能,求出第二年产品售价;若不能,请说明理由.

分析(1)设y与x之间的函数关系式为y=kx+b(k≠0),由图表可得出函数关系式,x的取值范围由图可知:100x180;

(2)设公司第一年的盈利为W万元,根据“利润=销售额−成本”,建立函数关系式:W=(x−60)y−1500,解出即可;

(3)由题意知,盈利总额=第二年的销售利润−第一年的亏损,解出对应的x值,根据第一问100x180,取适合的值作为答案;

解答(1)设y=kx+b(k≠0),则由图象知:解得:30,100x180

(2)设公司第一年获利W万元,则

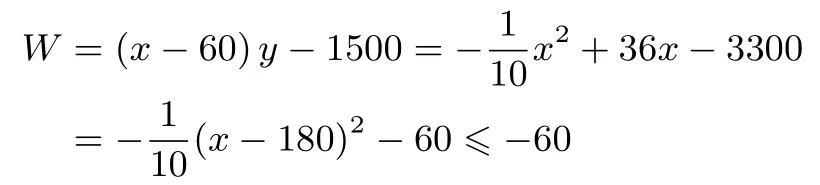
∴第一年公司亏损了,当产品售价定为180 元/件时,亏损最小,最小亏损为60 万元;

(3)若两年共盈利1340 万元,因为第一年亏损60 万元,第二年盈利的为则解得:x1=200,x2=160,∵100x180,∴x=160,即每件产品的定价定为160 元时,公司两年共盈利达1340 万元.

评价这道题综合考查了一次函数模型和二次函数模型.此题比较综合,难度较大.在解题过程中,首先要准确求出函数解析式,其次要根据题意列出方程.在确定最值和求解过程中,要注意自变量取值范围,从而对结果进行取舍.

3 函数模型思想方法在初中阶段的教学策略

学生在运用函数模型思想方法解决应用问题的过程中,遇到的主要障碍是如何将实际问题进行有效的“数学化”.佛莱登塔尔曾说“学习数学的本质就是学习数学化”,在这里数学化的关键是能否在问题与数学之间建立对应的必要联系,即创建数学模型,进而利用函数相关的知识解决问题.

一般而言,初中学生要理解、掌握、运用函数模型思想方法,必须具备以下三个条件:

(1)具备完善的函数相关知识;

(2)有良好的数学抽象能力;

(3)有较强的分析和问题解决能力;

因此,教师在函数模型思想方法的教学中应贯彻以下三个方面:

3.1 建立扎实的函数知识体系,为应用函数模型做好知识储备.

一切与函数模型相关的应用题型,除了考查学生将题目信息“数学化”的能力之外,考查的内核无外乎就是函数的相关性质.因此,教师在教学中要提高学生的函数模型应用能力,首先要帮助学生建立扎实的函数知识体系,为应用函数模型做好知识储备.

初中阶段,函数模型一般只涉及三种:一次函数模型、反比例函数模型、二次函数模型.教师在教学中,一定要让学生明晰各个函数模型的特点,为应用打下坚实基础:

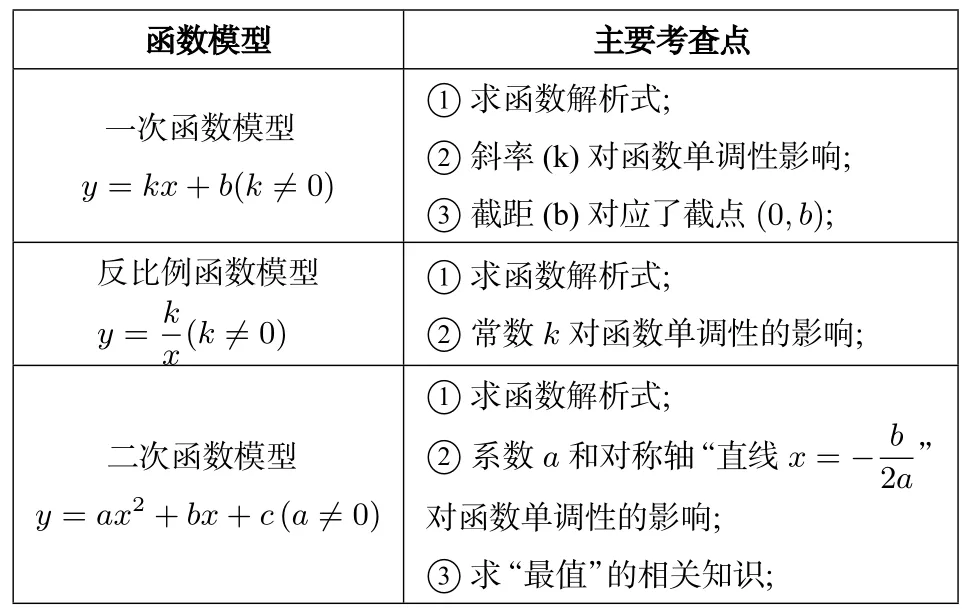
函数模型主要考查点一次函数模型y=kx+b(k≠0)①求函数解析式;②斜率(k)对函数单调性影响;③截距(b)对应了截点(0,b);反比例函数模型y=kx(k≠0)①求函数解析式;②常数k对函数单调性的影响;二次函数模型y=ax2+bx+c(a≠0)①求函数解析式;②系数a和对称轴“直线x=−b2a”对函数单调性的影响;③求“最值”的相关知识;

3.2 善于创设问题情境,提高学生函数应用意识[5]

课程标准中明确提出了“发展学生的数学应用意识”这一具体要求.贯彻数学建模思想在初中数学中的应用是提高学生数学应用意识的有效途径.教师在课堂中落实函数模型思想方法的教学就必须将教学内容与学生的生活实际紧密联系起来,善于根据所学知识创设问题情境,引导学生利用已知的数学知识解决问题,从而逐步提高学生的数学应用意识和能力.

例如,在讲解“二次函数”这一内容过程中,教师若能结合课本内容,建立与销售盈利问题相关的现实情境,让学生做“小老板”,依据情境借助“二次函数”知识去思考如何实现最大盈利,从而设计出最佳营销方案,让学生在知识应用中获得乐趣.这样既增强了学生的数学学习兴趣,又潜移默化地培养了学生的数学应用意识.

3.3 建立函数模型解题思维,提升学生数学抽象能力

知识的积累是函数模型及其他数学模型方法运用的前提.在函数模型教学中,教师应有意识地发挥示范作用,在增强学生数学应用意识的同时,还应让学生熟练掌握函数模型思想方法应用过程中的“建模—>用模—>解模”程序和步骤,培养学生形成良好的函数模型解题思维和严谨的解题习惯.此外,能否对现实问题进行有效的数学抽象是运用函数模型思想方法成败的关键.因此,教师在教学中,一定要学会对同一种基本函数模型进行多种变式训练,让学生在对比中发现解题方法的本质,从而增强对实际问题的数学抽象能力.