基于贝叶斯理论的含可信度孔隙压力随钻修正方法
2020-09-04胜亚楠管志川李伟廷蒋金宝晁文学孔华
胜亚楠 管志川 李伟廷 蒋金宝 晁文学 孔华
1.中石化中原石油工程有限公司钻井工程技术研究院;2.中国石油大学(华东)石油工程学院
地层压力的准确预测是保证钻井从设计到施工顺利安全进行的重要前提[1-3],因此,地层压力监测与预测一直是油气钻井的一项重要任务。目前,异常地层压力的求取方法主要分为以下几类[4]:钻前压力预测、随钻压力监测、地球物理测井压力检测以及压力实测。钻前压力预测主要是利用地震层速度资料及其与孔隙压力的关系模型计算孔隙压力,常用的方法有等效深度法、单点预测模型和综合预测模型等[5-8];但是由于地质情况的复杂性以及地震资料的精度等问题,孔隙压力钻前预测结果与井底实际压力之间存在较大的误差[9-10]。当一些钻井作业决策不得不依靠这些不充分、不准确或者不完整的孔隙压力信息制定时,可能会导致大量潜在的钻井作业风险的发生。钻前描述孔隙压力都要依据历史数据和周边井数据,所以不可避免地包含了某些不确定因素,一旦开钻这些数据都已过时,需要利用随钻测井、随钻测量和随钻地震等信息对钻前预测的孔隙压力进行实时修正。利用钻进过程中各种随钻和录井参数进行压力监测已在实际钻井过程中得到了广泛应用,起到了实时指导钻井工程的作用。利用这些实钻数据可以弥补钻前数据的不足,不断修正孔隙压力预测结果、降低其不确定度,这样就可以辅助钻井作业人员快速、准确地进行施工方案的决策,减少由于压力信息不准确带来的钻井作业风险。因此,如何根据随钻测量数据去动态更新孔隙压力预测结果,是本文将要解决的关键技术问题。Bayes理论提供了一种计算假设概率的方法,这种方法是基于假设的先验概率、给定假设下观察到不同数据的概率以及观察到的数据本身而得出。其方法为:将关于未知参数的先验信息与样本信息综合,再根据Bayes理论,得出后验信息,然后根据后验信息去推断未知参数。本文利用Bayes理论对含可信度孔隙压力的随钻更新与修正方法进行研究。
1 含可信度孔隙压力钻前预测方法
地层孔隙压力是井身结构设计的重要依据,由于深井复杂地层油气地质的复杂性、解释资料的不完备性以及数学模型的精度等问题,孔隙压力的真值是无法得到的,误差是客观存在的,因此孔隙压力的预测结果具有不确定性,真值会以一定概率形式分布于某区间内。石油大学管志川等提出了钻前计算含可信度孔隙压力的方法[11-12],根据的是地震层速度资料,采用的是Eaton法和Fillippone法相结合的方法。这种方法预测的结果不再是单一数值,而是具有可信度的区间。
2 基于Bayes理论的钻前模型随钻更新方法
2.1 随钻压力监测技术
目前常用的孔隙压力随钻监测方法有:岩石强度法、dc指数法和随钻测井预测法[13-15]。dc指数法是最为常用的孔隙压力监测方法,其实质上是机械钻速法。它利用泥页岩压实规律和压差对机械钻速的影响理论来监测孔隙压力。dc指数计算模型如下
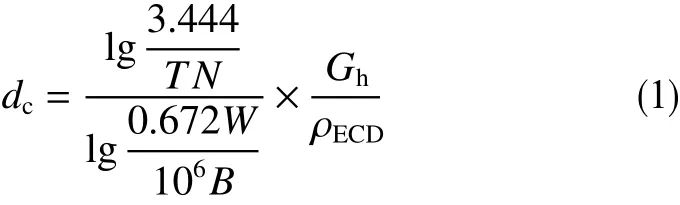
式中,dc为地层压力指数,无量纲;T为钻时,min/m;W为钻压,kN;N为转盘转速,r/min;B为钻头直径,为循环当量钻井液密度,为静水压力梯度当量钻井液密度,g/cm3。
根据dc指数进行异常地层孔隙压力预测,计算公式如下
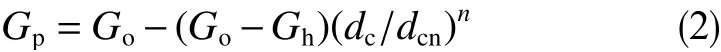
式中,Gp为孔隙压力当量钻井液密度,g/cm3;Go为上覆岩石压力梯度当量钻井液密度,g/cm3;Gh为静水压力梯度当量钻井液密度,g/cm3;dcn为对应深度的dc指数正常趋势值。dc指数的趋势线是在进入异常压力地层之前,找一段厚度相对较大、岩质较纯且成岩性较好的泥岩或页岩来确定。
随钻测井预测法是最为准确的压力监测方法,如果有随钻声波测井或者随钻电阻率测井资料,可以根据这些随钻资料,利用等效深度法、伊顿法或有效应力法进行随钻孔隙压力预测;电阻率、声波时差的正常趋势线的处理方式与dc指数法相同。
2.2 贝叶斯方法基本理论
目前,在国际上解决地球物理反演过程中的不确定性问题中,最常用的方法是基于概率的贝叶斯方法,通过将模型参数的先验信息与观测信息相结合来推断其后验概率分布,从而更新钻前模型。借鉴贝叶斯方法在地球物理反演领域内的应用,本文选用贝叶斯方法对钻前构建的含可信度孔隙压力进行动态更新与修正。
贝叶斯方法提供了一种计算假设概率的方法[16],这种方法是基于假设的先验概率、给定假设下观察到不同数据的概率以及观察到的数据本身而得出的。其方法为:将关于未知参数的先验信息与样本信息综合,再根据贝叶斯公式,得出后验信息,然后根据后验信息去推断未知参数。假设需要估计的参数为θ ,x是与 θ有关的观测样本,利用贝叶斯推断可以求取参数θ 的后验分布概率
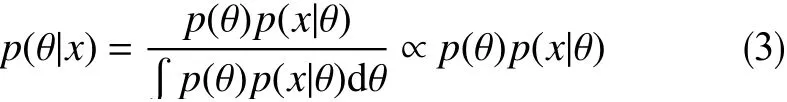
式中,p(θ|x)为后验概率密度;p(θ)为先验概率密度;p(x|θ)为似然函数。通过后验分布可以对 θ参数概率分布进行期望和方差的估计。
根据贝叶斯定理可以推导出下面一系列表达式


2.3 基于Bayes理论的钻前模型更新方法
根据第2小节计算模型可以在钻前获得的一口井沿井深分布的含可信度孔隙压力剖面,将任意深度上含可信度孔隙压力概率分布信息用均值和方差表示,记为随钻更新钻前模型可以归结到更新任意深度上孔隙压力的概率分布问题。本文利用Bayes理论对钻前模型进行更新与修正,首先根据随钻资料得到钻头位置附近的随钻压力监测结果,再基于迭代Bayes理论实时修正钻前孔隙压力的概率分布模型。基于贝叶斯定理进行孔隙压力随钻更新具体步骤如下。
假设变量p为含可信度孔隙压力钻前信息,其概率模型为

式中,µ为总体期望,ε为不确定度误差项,它服从均值为0、方差为σ2的正态分布,即ε ~N(0,σ2)。
其概率分布密度函数为

为了进行贝叶斯分析,需要首先确定模型参数的先验概率分布;根据前文构建的可信度孔隙压力的钻前概率剖面,可以得到孔隙压力的先验概率分布为:因此,孔隙压力p的先验概率密度函数为

基于随钻孔隙压力预测结果,得到了相应的观测样本为

观测样本概率的具体求解过程如下:假设钻头上部在井深ΔH范围内有m个孔隙压力随钻监测结果,将其作为一组测量样本为样本区间,其值取该样本地层层组内理论变异函数模型变程的两倍;然后采用正态信息扩散估计求取孔隙压力观测结果的概率分布。采用正态信息扩散估计求取地层压力观测值的概率分布,设地层压力观测值M的概率密度函数为f(x),最终推导得到地层压力观测值M概率密度函数f(x)的正态信息扩散估计[17]为

h为扩散系数,假设孔隙压力观测值X在目标观测井深范围内的最大值为xmax,最小值为则h为


表1λ值与样本数m的对应关系Table 1 Corresponding relation between λand sample number m

根据贝叶斯共轭分布理论[18],孔隙压力p的后验分布也是正态分布;将先验概率密度函数与似然函数代入贝叶斯公式,得到后验概率分布为

其中

根据式(14)可以得到含可信度孔隙压力p的后验概率分布:孔隙压力后验概率信息综合了钻前孔隙压力先验概率信息以及随钻孔隙压力观测概率信息,最大限度地保证了钻进作业过程中钻头位置局部孔隙压力预测结果的准确性。
3 实例计算与结果分析
本文选取一口探井XX井为例进行实例计算与结果分析。图1为XX井钻前压力预测结果,从图1可以看出:1 500 m之前压力系数在1.0~1.2之间波动,属于正常静水压力体系;而从1 500 m以下,压力开始逐渐抬升,1 750 m左右井深位置处孔隙压力系数达到最高值1.6。异常高压的存在严重影响了钻井安全,因此需要在井深1 500 m井段时开始进行随钻压力监测,为钻井作业过程中动态风险预测提供更为准确的压力信息。从1 500 m处开始,利用随钻测量工具得到300 m井段(1 500~1 800 m)的随钻声波以及随钻电阻率测井资料,如图2所示;并依据伊顿法利用随钻声波及电阻率测井资料进行孔隙压力的随钻预测,最终得到孔隙压力随钻预测结果,如图3所示。

图1 XX井钻前含可信度的孔隙压力剖面Fig.1 Pre-drilling credibility containing pore pressure profile of Well XX

图2 XX井随钻声波时差和随钻电阻率测井资料Fig.2 Interval transit time log while drilling and resistivity log while drilling of Well XX

图3 XX井1 750~1 760 m地层孔隙压力随钻监测结果Fig.3 Result of pore pressure monitoring while drilling in the interval of 1 750~1 760 m in Well XX
利用本文建立的随钻模型更新方法,对1 760 m井深位置上含不确定度的地层压力钻前预测结果进行随钻动态修正与更新,流程图如图4所示。
首先,从钻前模型中提取XX井含不确定度的地层孔隙压力剖面,从中获得XX井在1 760 m井深位置上孔隙压力钻前先验概率分布为:N(1.38,0.0942);然后取1 760 m钻头位置上部1 750~1 760 m井段随钻地层压力监测结果,将其作为观测样本,采用正态信息扩散估计求取该样本集合的观测样本概率,作为观测概率信息:N(1.436,0.0272);最后,基于贝叶斯理论通过数学推导得到地层压力的后验概率信息:N(1.406,0.0742)。地层压力后验概率信息综合了钻前地层压力预测信息以及随钻地层压力观测信息,在钻前预测的基础上利用随钻资料进行了修正与更新,使得地层孔隙压力的不确定度减小,提高了预测结果精度,可以为钻井作业过程中动态风险评估提供更为准确的地层压力信息。

图4 XX井1 760 m孔隙压力随钻更新流程图Fig.4 Process of pore pressure upgrading while drilling at the depth of 1 760 m in Well XX
4 结论与建议
(1)采用贝叶斯方法对地层孔隙压力的不确定性进行更新和修正,从理论和实践上都是可行的。
(2)利用Bayes理论实现了对含可信度孔隙压力的随钻更新与修正,为钻井作业过程中动态风险评估提供实时且更为准确的孔隙压力信息,可以辅助钻井作业人员快速、准确地进行施工方案的决策,减少由于压力信息认识不准确带来的钻井作业风险。
