基于混沌算法的不对称交通信号模糊控制系统设计

曹秀爽 张志军

（1、唐山工业职业技术学院自动化工程系，河北 唐山063000 2、首钢京唐钢铁股份有限公司，河北 唐山063000）

随着社会的进步和人们对美好生活的向往，汽车保有量一直连年攀增，有限的道路资源成为城市管理的瓶颈，交通信号灯配时的不合理一定程度上造成绿灯时间的浪费，降低了道路利用率，当前大多工业区的建立，使得居住区的居民需要每天往返于居住区和工业区之间，这样交通流呈现多呈现“潮汐特性”，统的定时配时设置不能很好的控制协调不平衡的交通流量，要缓解潮汐特性路口的交通早晚轮番拥堵的现状，不对称配时被提出，这是一项治理拥堵的简单有效的技术措施。

那么如何合理的设置不对称信号配时，才能够降低交叉口通行延误，以达到确确实实能改善具有潮汐特性路口的通行能力呢？很多学者纷纷进行了大量的研究，文献[1]针对交叉口的交通流量不对称情况，性能指标选为车辆的平均延误时间，利用SAGACIA 优化方法优化不对称配时参数，优化产生一组不对称绿灯信号配时，对此类路口的交通状况起到了改善作用。但是，城市交通控制系统是一个具有较大随机性、复杂性的非线性系统，很难建立精确的数学模型，而模糊控制不依赖于被控对象的数学模型，很多学者将模糊控制应用到了交通领域[2]，由于模糊控制规则等参数获得要依靠人们的经验，具有主观性和随机性，在交通流量不对称比较严重的交叉口，控制效果不是很理想；本文将模糊控制和混沌优化方法应用到交叉口的信号配时，根据交叉口的交通流量变化，采用借相位设置依次通行的不对称相位，性能指标为车辆的平均延误时间，应用混沌算法优化模糊控制规则，输出各相位不对称的绿灯配时。

在优化领域混沌算法优越独特的特性被广泛的应用，对模糊控制器控制规则和隶属度函数等参数进行优化，在优化过程的中对要优化参数用实数进行编码，利用混沌的遍历性使得不易陷入局部最优，得到性能更优的下一个新解，使得逐步向最优解方向靠近。

本文通过混沌算法优化不对称配时的模糊控制器的模糊控制参数，并将优化后的不对称模糊控制器用于具有“潮汐特性”的四相位交叉口交通信号控制。

1 具有潮汐特性交叉口的相位设计

在交叉口的安全性和通行能力方面考虑，合理的相位的设计起到很大作用，如果相位顺序不合理，相邻的相位在发生转换时刻容易发生车辆碰撞，特别是具有潮汐特性的交叉路口，在交通高峰时段这种现象更为明显，使得路口通行效率低，时常出现闯红灯现象。

1.1 设置时段。对于交通流量不对称的交叉口，根据其所具有的潮汐特性，可以设置不对称的绿灯配时方案和合理恰当的相位顺序，根据各进口道在不同配时时段内交通流量的多少，把流量不对称交叉口划分成早晚高峰、平时时段及夜间时段，并且具有不同的绿灯配时和相位顺序。由于篇幅限制，这里以早高峰的绿灯配时及相位顺序设计为例。

1.2 设置相位。研究对象为流量不对称的干支交叉路口，因为主干路上车流量大，所以设置相对应的不对称绿时配时及相位顺序；而支路上车流量较小，所以设置相对应的对称配时及相位顺序，并且均采用先直行后左转放行方式，避免相邻相位的车流发生冲突。不对称路口的相位顺序设置如图1 所示。

第一相位为干路上南北方向直行通行，第二相位为北向南直行同时可以左转，该相位时直行的车流量大，当直行方向车流的流量平缓之后，直行通行停止，直行车流和左转车流没有交叉，同时放行互不影响，称为借相位放行,节省了时间，减少了北向南直行通行车辆的延误。直行车流无形中多放行了一部分时间，可以看出该相位顺序缓解了车流量大的入口方向的车辆延误；第三相位为南北同时左转，当直行车流停止通行后，南北同时放行左转，此时左转车流实现了不间断的放行时间，也同样增加了左转车道放行的通行时间；第四相位设置在支路上，支路上车流量相对较小，我们把直行左转设置为同时放行。

2 模糊控制器设计

2.1 系统控制方案设计。模糊控制器的输入分别为当前相位的车流量和下一相位的车流量，模糊控制器的输出为下一个相位的绿灯车辆通行时间。模糊控制的不对称交通信号控制系统如图2，其中qi 和qj 分别为当前相位和下一相位的车流量，构成模糊控制器的精确输入值；t 为下一相位的通行绿灯信号时间精确值；QI、QJ、T分别为精确值qi、qj、t 的模糊变量值。

2.2 输入变量定义及模糊化。输入变量为当前相位与下一相位的交通流量，模糊化运算模块的作用是将输入的精确量转化为[0，1]上的模糊量，也就是要知道模糊集的论域，以及所应用的隶属度函数和模糊集的数量。设当前相位qi，下一相位qj，规定模糊化运算的输入变量qi 和qj 的取值范围为[0，40]，将论域划分为11 个等级，则11 个模糊论域{0，1，2，3，4，5，6，7，8，9，10}. 量化因子K1=K2=0.25，凭经验获得。实际值q 相对应的模糊论域的Q=[q/4]，[x]表示不大于x的最大整数。QI 和QJ 的模糊语言值设置为｛很少，少，较少，中等，较多，多，很多｝，选取三角形隶属度函数作为输入的模糊子集隶属度函数。

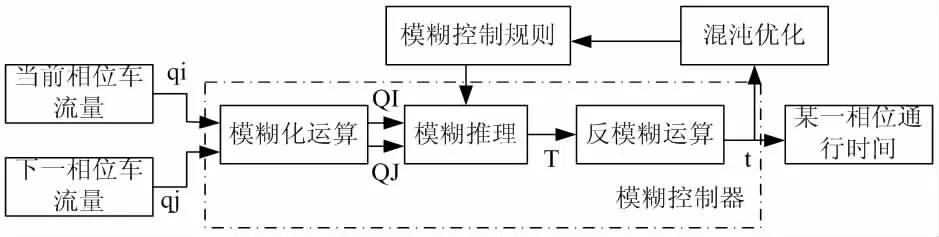
图2 控制系统结构框图

2.3 输出变量定义及模糊化。输出变量为下一绿灯相位的绿灯时长t，定义输出变量t∈[0，40]s，将论域划分为11 个模糊论域｛0，1，2，3，4，5，6，7，8，9，10｝，比例因子K3=0.25，实际值t 相对应的模糊论域值T=[t/4].T的模糊语言值｛很短，短，较短，中等，较长，长，很长｝。选用三角形分布函数作为模糊子集的隶属度函数。

3 混沌算法

3.1 混沌思想。混沌现象普遍存在于非线性系统中，该现象的特点是具有遍历性、随机性、“规律性”；将混沌量映射为待优化量采用了“载波”的方法实现，并把其遍历范围也变换成待优化变量的合适的取值范围，算法优化过程中进行搜索求解利用了混沌变量的特性，其具有的特性使得算法搜索求解更加准确有效[3]。

3.2 混沌算法基本步骤。Step 1.初始产生不同轨迹的混沌待优变量。Step 2.用载波的方式产生待优化变量；并将变化范围“放大”到相应论域范围。Step 3.用新产生的混沌变量迭代搜索，计算相应的性能指标，并且和原指标相比较。Step 4.用随机扰动方式在当前最优解附近进行若干步的细搜索，得到对应的性能指标，如果优于当前最优解则保留，否则丢弃。Step 5.判断事先设置的迭代次数，如果达到迭代次数，则输出最终最优解并终止搜索；如果没有到达迭代次数返回step3 继续进行搜索求解。

4 模糊控制器的优化

4.1 解群设置。以每两个相位的车流量为输入，对应的输出为一组数据，定义解群为4×3 的矩阵，第一列和第二列分别为四个相位，第三列是输出相位的输出绿灯时长，解的基本结构如下：

4.2 解的不对称优化设置。所设置的解的结构中，输入为第四相位和第一相位的车流量时，绿灯时间t1 是模糊控制器第一相位输出，为南北方向直行；第一相位和第二项位的车流量作为输入时，模糊控制器输出第二相位绿灯时间t2，为北向直行和北拐东；输入为第二相位和第三相位的车流量时，绿灯时间t3 为模糊控制器第三相位输出，为南北左转绿灯时间；输入为第三相位和第四相位的车流量时，绿灯时间t4 为模糊控制器第四相位输出，为东西向直行、左转的时间。

5 实例验证及分析

本文选用唐山市一个不对称交通流量的干支交叉路口（建设路和朝阳道交叉路口）为研究对象，建设路为南北方向主干道（双向八车道），朝阳道为东西方向支路(双向两车道)，早晚高峰时主干道上交通流量严重不对称，所以设置相应相位顺序和不对称信号配时配置，能够缓解交叉口车辆延误，提高路口在高峰期的通行能力。假设交叉口每个方向车辆随机到达，平峰时模拟采用泊松分布规律，高峰时模拟采用二项分布规律，仿真时需要把所有车辆都换算成当量小汽车数量。车流量大的一和三相位的饱和流量为3600PCU/h，车流量较小的二和四的饱和流量为2880PCU/h，如果交叉口车辆到达概率小于1000PCU/h 时，经验上认为交通处于平峰时段，大于1000PCU/h 时，经验上认为处于高峰时段。仿真结果如表1 和图3 所示。

表1 模糊控制规则表

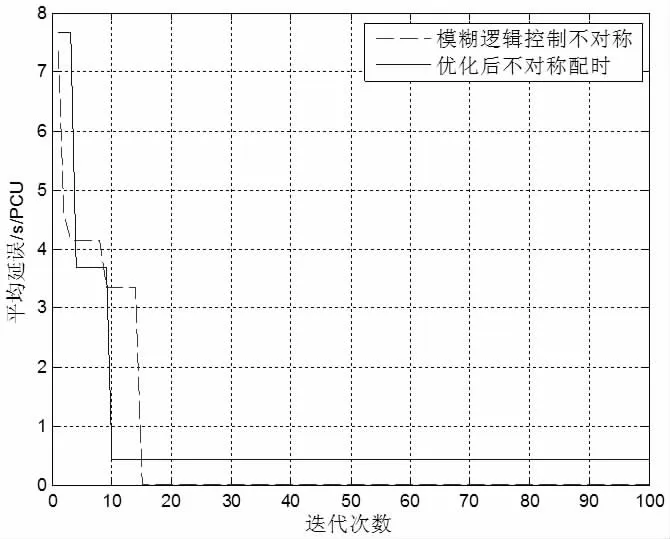
图3 仿真结果

从仿真结果可以看出，经过混沌算法优化模糊规则后，应用模糊控制对具有潮汐特性的交叉口进行不对称配时控制时，比普通定时优化不对称配时的控制效果好，车辆的平均延误收敛虽然慢一点，但是平均延误明显减小，使得交叉口的车辆通行效率有明显改善。

6 结论

本文研究了一个具有“潮汐”特性的干支交叉口交通信号的模糊控制方法，以交叉口的车辆平均延误为模糊控制交通信号的性能指标。利用混沌优化算法优化了模糊控制规则，混沌算法具有遍历性、随机性和规律性的特点，避免了搜索过程陷入局部最优，使得解群不会处于停滞不前状态。以交叉口车辆平均延误作为性能评价指标，对混沌算法优化后的模糊控制器控制的不对称交通信号配时进行了仿真研究。结果表明，优化后的模糊控制器比靠经验获得的模糊控制器能有效减小交叉口车辆平均延误；采用模糊逻辑控制的不对称交通信号配时比固定的不对称交通信号配时更能有效减小交叉口车辆平均延误。