复杂岩溶区溶洞储水与隧道衬砌相互作用

刘 鸿

(招商局重庆交通科研设计院有限公司,重庆 400067)

在高水压富水的岩溶区修建隧道,确定隧道合理的防排水方式及衬砌背后水压力,是隧道结构设计的关键技术之一,关于衬砌水压力的研究,一直是工程界关注和争论的焦点。

对于隧道衬砌水荷载的计算目前有两种计算模型:①基于Darcy定理的“渗透场”模型[1-5]；②水压作用下“荷载-结构物”模型。在第一种模型的计算中,“水荷载”表达为均匀分布在围岩和衬砌中的场力(体积力)。实际上,采用这种连续体模型将围岩和衬砌作为共同作用的整体,直接通过分析隧道开挖所引起的地应力和地下水渗透力对围岩和衬砌结构的联合作用进行围岩稳定性和衬砌的可靠性的评估,无须涉及“衬砌水压力”这一概念。

而在对“荷载-结构物”模型的水作用进行计算时,衬砌单独地承受衬砌范围内的渗透力,由于衬砌厚度相对于隧道埋深和隧道净空量较小,可将这种渗透力(体积力)简化为作用在衬砌外缘的表面力,称为“衬砌水压力”[6-7]。从衬砌结构的透水能力的角度出发,可将衬砌水压力分为两种[8-12]:①k1=0,即衬砌完全不透水。隧道开挖后,将在地层内部形成一个不透水的界面,根据水力学的静水压力传递原理,即可知在这种情况下衬砌将承受同初始静力水头相应的法向作用力。②k1=C(C为常数),衬砌具有一定的渗透能力。

本文所研究问题来源于已处运营期的铜西隧道,隧道在施工期间揭露多处溶洞,下雨时有大量涌水,如图1所示。依据具体的工程情况,表明“渗透场”模型已不再适用:①隧道衬砌采用高标号防渗混凝土；②溶洞的存在破坏了研究范围内围岩均质连续的假定；③隧道初衬与二衬间铺设有强化防渗高分子材料。以上几点否定了“渗透场”模型的基本假定；故该隧道的衬砌的破坏区别于渗透破坏。因此,本文将着重研究隧道衬砌在背后溶洞储水过程中的力学响应规律,找出并确定隧道衬砌开裂病害产生的原因。

图1 铜西隧道降雨期涌水现场Fig.1 Water injection in Tongxi tunnel in the constrcution and operating period

1 工程背景

已运营的铜西隧道地处酉阳县铜鼓乡,进口段位于铜鼓乡幸福村,进口北侧约900 m为S304省道,距酉阳城区路程约15 km；出口位于铜鼓乡铜西村,出口西侧约720 m为铜西村集镇,距酉阳城区路程约21.4 km。

现场调研揭示,铜西隧道左线二衬ZK12+930～ZK13+060段运营期间出现大量裂缝,下雨期间有大量地下水从隧道二衬间喷出,对隧道结构的稳定及过往车辆的安全造成重大影响,如图1所示。研究区的隧道围岩为三叠系下统大冶组灰岩,中至厚层状构造,岩体较完整,为坚硬岩,其强度大、稳定性较好,岩层倾角50°～60°。隧道的断面尺寸如图2所示。

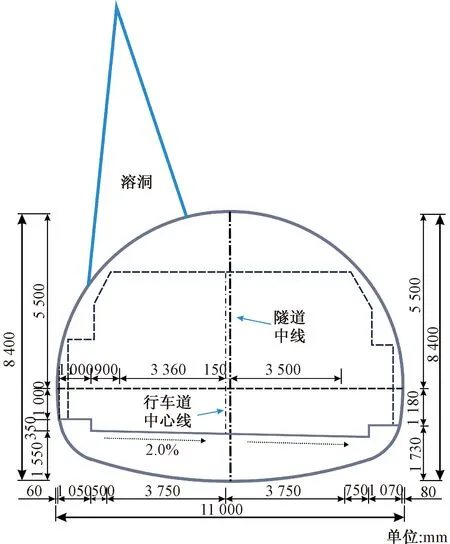
图2 铜西隧道断面尺寸示意Fig.2 Tongxi tunnel section size

2 溶洞储水模型研究

2.1 二维溶洞储水模型

由于工程区岩溶发育的复杂性,隧道在运营期间,隧道围岩中发育的溶腔溶缝因地下水运动或地表降雨汇集于衬砌背后。开始时,汇集得岩溶水通过隧道排水系统排走,但随着后续汇集水量的增加,岩溶水在向下流动过程中,夹带大量的杂质碎屑,将排水通道堵塞,导致衬砌承受的水压力越来越大,最后到达结构的强度极限发生破坏。

在确定衬砌破坏是因为隧道排泄系统堵塞后短时间内溶洞汇聚高水头水压致裂破坏之后,问题研究的重点转移到外水压力的确定,而外水压力的确定主要与溶洞的体积、汇水量及汇水时间密切相关。基于该工程区降雨统计,可假定溶洞在降雨时其汇水流量基本稳定,基于溶洞形态特点对溶洞的几何模型进行适当简化,建立溶洞在汇水期间的平均流量与衬砌所受压力的关系,进而分析衬砌结构的受力变化规律。

施工期间查明,铜西隧道左线开挖在ZK13+025拱顶处发育有一横向约3 m宽、纵向延伸接近40 m,断面呈锥形状的一个较大溶洞。在ZK12+960处又发现一宽4 m,高6 m一条溶洞,空间形态呈椭圆柱状,从右边墙拱腰一直向上延伸,目测溶洞高度在9 m左右。在ZK13+330附近发现拱顶处有裂隙,裂隙一直向上延伸,横向约1.19 m宽,呈喇叭口形状,长轴方向近似于隧道轴线平行。尽管ZK12+930～ZK13+060区间内发现的多处溶洞虽然空间形态各有所异,但它们具备了一些基本共同点:①溶洞洞壁整体较为平缓,未见明显大的起伏；②溶洞最宽或最窄方向之一近似平行或小角度斜交隧道纵轴线方向,且延伸长度均大于断面尺寸,因此将该类型溶洞称为“走向型”溶洞,而这类问题简化为平面应变问题进行研究。

对于“走向型”溶洞,以ZK13+025处锥形溶洞为例,建立如图3的水压力与汇水量之间的换算模型,由此可计算出一定时间汇水量对应的水压力,在考虑围岩压力前提下通过数值方法分析水压对围岩和隧道结构的影响。如图3,以隧道上部分圆形轮廓线圆心为坐标原点建立直角坐标系,溶缝两壁简化为平面直线,分别对应直线L1与L2。两壁与隧道衬砌的交点分别为A、B,圆弧AB对应的圆心角为θ。水流汇聚时不考虑水流对衬砌结构的冲击作用,衬砌仅受到静水压力作用。

图3 二维溶洞计算模型Fig.3 2D karst cave calculation model

现设直线FD与FE的方程为

(1)

弧线AB的方程则为:

x2+y2=R2，θ∈[θ1,θ2]

(2)

在第一阶段中,汇水量为曲边三角形IMA面积,现假设水位线达到MI,MI的解析表达式为Y=y,所以,曲边△IMA面积为

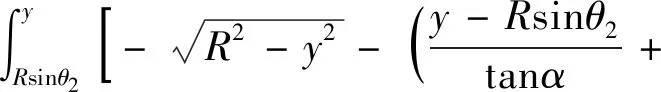
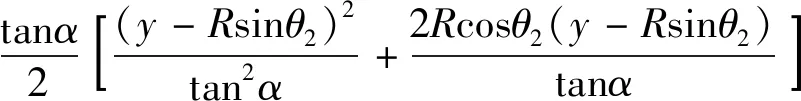
(3)

由式(3)可得第一汇水阶段任意水位下的储水体积,继而可以换算出作用在衬砌上的静水压力；当水位面到达PB时,有y=Rsinθ1,代入式(3)可得:

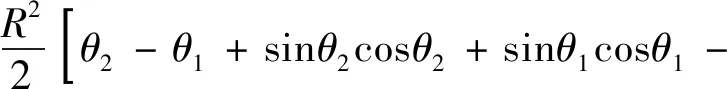
(4)

此后,当水位继续增加至F点,其最大水压力可由式(5)、式(6)求得:

(5)

(6)

2.2 空间溶洞储水模型

对于几何外形较为规则的空间“斜交型”溶洞就不再使用平面模型进行研究,特别当隧道断面以及溶洞体积、高度较大时,求解溶洞中的储水体积是求解衬砌内力的关键。但无论几何外形多复杂的规则溶洞(如四棱柱型、多棱柱型等),都可以通过四面体溶洞的体积求解方法与思路进行拓展和演绎。

如图4所示,由地质学知识可知,结构面法向向量的三个分量可表示为

n=(nx,ny,nz)=(nsinαsinβ,nsinαcosβ,

ncosα)

(7)

图4 结构面与隧道坐标转换示意Fig.4 Coordinate transformation of discontinuity surface and tunnel

隧道与溶洞的空间位置如图5所示,隧道上部分断面为一圆形,其空间方程可由式(8)表示,三个斜平面方程由式(9)表示。联立式(9)三个方程,可求出三面的交点以及三交点坐标。

图5 三维溶洞计算模型Fig.5 3D karst cave calculation model

(8)

(9)

现简化A、B和C点三点坐标分别为(x1,y1,z1)、(x2,y2,z2)、(x3,y3,z3),因此,可通过该三点确定一个通过该三点的平面,假设平面方程表达式为ax+by+cz+d=0。但为了后续理论及公式的方便表达,继续采用平面方程表达式:ax+by+cz+d=0。

首先求解由三个交点所在平面与顶点构成的标准四面体体积；继而求解由曲面ABC和平面ABC构成的弓形体,二者之差即为目标体体积。

对于弓形体准确体积求解过程叙述如下:现假定平面三角形ABC三条直边AB、BC和AC沿Z轴正向向上延伸,分别与隧道圆柱面相交形成三条新的曲线AB2、AC2和BC2,则由此三条新曲线确定的隧道弧面与平面ABC就又形成了一个新的弓形体Vnew。Vold的体积等于Vnew体积与三个侧向辅助小弓形体体积之差。

由解析几何和二重积分知识可知,Vnew弓形体体积可直接由二重积分在XOY平面上的投影域求得,被积函数为隧道圆柱面与平面ABC的高度差。因此,Vnew体积可由式(10)求解:

Vnew=∬D1(ztunnel-zABC)dxdy+∬D2(ztunnel-zABC)dxdy

(10)

V1求解因求解中表达式的复杂性,所以需将求解表达式进行多部分的单独求解,最后再汇总:

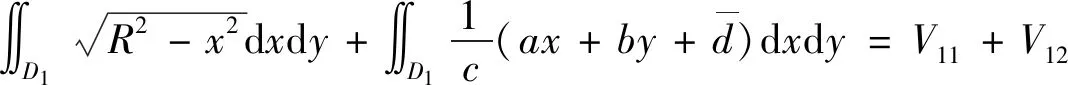
(11)

(12)

至此V11求解完成,V12的计算可按照上述步骤完成。

(13)

对于V2的计算,其计算过程与V1相同,差别仅在于积分上下限不同,此处不再赘述。曲线A′B′为结构面ABP与圆柱面的交线在XOY平面上的投影线,它与直线A′B′围成的区域即为积分区域,所以V3求解表达式为

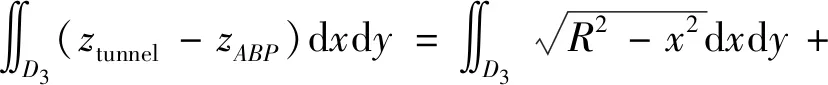
(14)

V31和V32的计算结果如下:

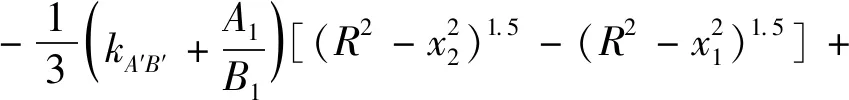
(15)

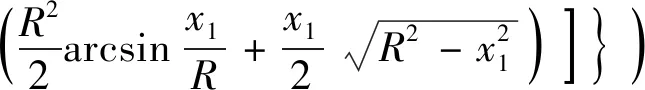
(16)

3 数值模型

3.1 模型概况

建立如图6所示的有限元模型,将其简化为平面应变问题。有限元模型的空间尺寸为宽(Y方向)×高(Z方向)为84.0 m×100.6 m,隧道轴向为X方向,隧道上半圆半径为5.95 m,隧道净高为9.3 m,跨径为11.9 m。有限元模型要尽可能接近实际情况,因此考虑了一定的地形因素,隧道最大埋深约63.4 m,两条溶洞轮廓线L1和L2斜率角分别为α=84°和β=108°,溶洞对应隧道圆弧圆心角为θ=41°。围岩采用2D固体单元模拟,本构模型采用摩尔库伦模型,共划分3 467个四边形单元；衬砌结构采用梁单元模拟,其应力应变关系符合胡克定律,模型如图6所示,有限元计算参数如表1所示。

图6 “水压力-结构”有限元模型Fig.6 “Water pressure-structure” finite element model

表1 数值模型计算参数

3.2 荷载模拟

一般定义作用在衬砌上的外水压力水头与地下水位到隧道的水柱高之比为外水压力折减系数[13-16],同时结合现场水文地质条件综合确定。目前有关外水压力计算时所采用的外水压力折减系数主要是依据水电部门《水工隧洞设计规范》的相关规定,水压计算公式如下:

P=βγwH

(17)

式(17)中：P为外水压力；β为外水压力修正系数；γw为地下水重度；H为地下水水头。研究段隧道约为58 m。根据雨季时现场渗漏水情况可认为处于严重股状流水；综上所述,荷载计算过程中,外水压力折减系数可取β=0.85。由上可得作用于隧道表面的水头压力为

P=βγwH=0.85×10 000×58≈0.5 MPa

(18)

ADINA空间函数用于控制指定区域的荷载作用分布形式:如矩形、三角形分布等。时间函数用于控制荷载随时间变化的特性。水压力的变化只与水位差相关,且同一深处各向静水压力相同。水位从A点到F点过程中,因为不同水位下水压作用区域也不同,无法直接模拟水位变化的影响,采用16个模型模拟16个水位下的变化情况。当水位超过F点后,因无具体的荷载作用域,故可控制荷载函数来改变不同水位下的水压力换算模拟继F点后水位继续增长对隧道的影响情况。根据模型水压力分布如图7所示。

4 模拟结果分析

4.1 溶洞左侧壁

LINE1 主要研究了溶洞左侧壁在溶洞积水过程中其位移与应力的变化情况。如图8所示,溶洞左壁模拟结果分析的主要内容包括洞壁水平位移和第一主应力。

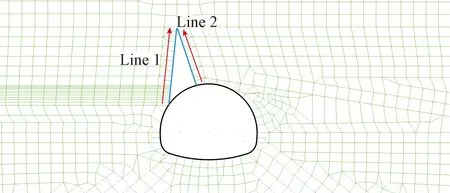
图8 数据提取位置示意图Fig.8 Schematic diagram of data extraction location

图9(a)中由于前10个水位线划分高度较密,导致位移曲线变化很不明显,但仍可获得LINE1水平位移分布趋势。在随后的6个水位作用下,位移变化较为明显,由左至右曲线呈下降趋势,前半段型近似为一“下凸”形态,位移方向主要指向临空面,这是因为在计算时平衡模型初始位移后继续受到水压扰动后的结果。侧壁底部是正位移的最大区域,受水压作用其大小由0.14 mm减小至0.11 mm,水位影响率为0.03/10=0.3%。曲线后半部分接近直线分布,侧壁顶部是最大负位移集中区,其位移约从0.04 mm增至0.06 mm。

当水位漫过溶洞继续增长后,位移曲线的形态发生明显的转变,由前述单调递减型转变为抛物线型,所有位移值均为负值,表明侧壁位移已经开始背向临空面。曲线变化受水压影响十分明显,最大位移由1.4 mm增至6.5 mm,水位影响率为5.1/33=15.4%。又因为上下边界的限制,溶洞侧壁简化为受到法向荷载作用的两端固定的梁,对应中间位移较两端都大。

如图9(b),同样忽略首尾单元的影响,第一主应力的分布曲线仍呈递减型分布,但第一主应力受到的影响更为明显。后期的分布趋势都为“上凸”型,表现因为中间受到影响较两边界更明显。第一主应力均表现为负值,表明此处围岩暂时未受到拉应力的作用。

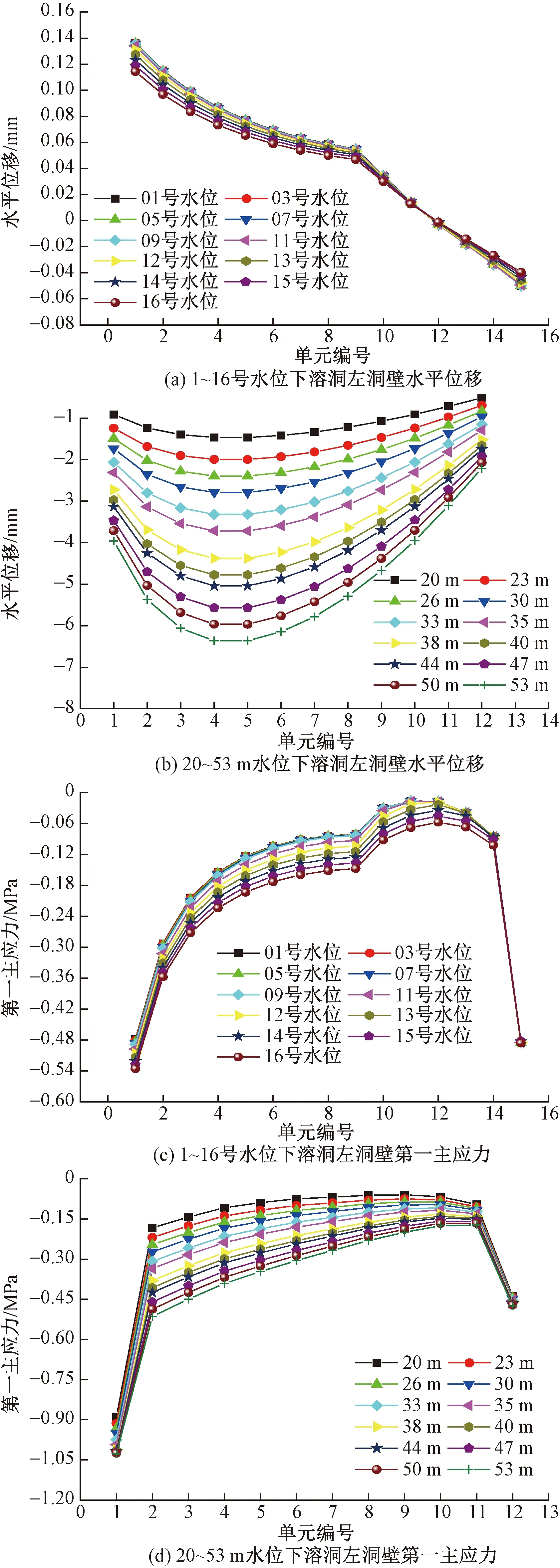
图9 溶洞左侧壁汇水过程力学响应规律Fig.9 Mechanics change of karst cave left side during impoundment

4.2 溶洞右侧壁

由图9可知,鉴于1～10号水位的影响作用不明显,而图10(a)显示溶洞壁位移受临空面影响大,水位间接影响作用弱；直至水位开始起直接作用,随着水压增大位移开始逐渐减小并又重新反向增加。曲线分布由原来的递减型变为“上凸”型,正方向最大位移约1.5 mm,受模型两端的影响,负位移越靠近顶部变化越明显,最大值接近-1.0 mm。实际环境中,溶洞顶部的开口宽度缩窄,也会引起应力集中现象,从模拟结果看来,两个相反方向位移的过渡区必定承受了高剪应力,对围岩稳定影响最大,其次为洞壁中部区域。

图10 溶洞右侧壁汇水过程力学响应规律Fig.10 Mechanics change of karst cave right side during impoundment

如图10(b),11～16号水位作用下第一主应力出现波动情况,同一水位下平均最大应力集中范围0.2～0.25 MPa,在后期水压作用下,波动起伏现象明显减弱,曲线呈递增分布,但实质应力是呈递减趋势。应力波动现象除了与模型几何参数,受力大小等因素相关,最重要的是整个洞壁水压力变化特点:①1～16号水位作用下,洞壁水压力作用形式主要为三角形分布,且水压范围在不断变化；②后续水位增加,水压作用范围可认为已不变,荷载继续增加其分布形式开始转变为梯形分布；③最后,研究范围内洞壁高度有限,与作用水位高度相比,其荷载作用形式虽为梯形分布,但作用效果与该区域的矩形荷载作用离散会越来越小。

4.3 衬砌内力响应

由图11(a)、图11(b)可知,水位变化过程中结构内力均有所增加,而其中轴力沿衬砌分布较均匀,其趋势改变不明显。剪力则是两处拱脚,左边墙以及拱顶区域较大；水压增加未对左边墙及拱脚的剪力分布形态造成明显影响,而拱顶及右边墙的剪力却有所降低；最后如图11(e)、图11(f)所示,水压增加导致弯矩分布形态较为明显,主要集中于右侧边墙、拱腰及拱顶近溶洞区,因此在静水作用下对应部位混凝土易受拉开裂；现场调研结果显示边墙部具有较大裂缝,拱腰与拱顶部渗水严重(图12),与计算结果相符。

图11 水压作用下衬砌内力响应Fig.11 The internal force of tunnel lining under water pressure

图12 边墙破裂形态现场图Fig.12 Failure characteristics in Tongxi tunnel

5 结论

(1)由现场照片可知,局部范围内衬砌在破坏的同时出现了渗流现象,而另外其他范围内的衬砌则是先开裂后有渗水。通过以上的研究可知,衬砌破坏的最主要原因为高水头静水压力下的力学破坏,而并非水体的渗透破坏；衬砌破坏过程中先由高水压破坏,降低结构的强度完整性和防渗性,同时高水头流体渗入软弱区,其水压劈裂作用和弱化作用进一步加剧瓦解结构强度,两种破坏模式相辅相成,共同导致最终的失效。结合实际工程衬砌结构的特点,该隧道的排水条件为衬砌均匀透水的假定也完全不合适,即“渗透性”模型不适用该类情况。因此该隧道工程的衬砌水压力模型应该属于“荷载-结构”类型。

(2)基于“荷载-结构”的衬砌水压力学模型的基本假定,推导了“走向型”溶洞和 “斜交型”溶洞体积基础计算公式,其他复杂溶洞体积计算方法可由此基础进行组合或演变。在知晓溶洞的体积后,进而可计算单位时间内的汇水体积,换算为衬砌水压力。汇水量与衬砌水压的关系即为衬砌结构的力学边界条件,本研究的理论推导有很好的通用性,并为类似工程的研究提供思路。

(3)由模拟结果可知溶洞与衬砌的位移变化相比应力更为明显,相应的水压力变化形态也由无水压力作用到三角形水压,再到梯形水压,最后为均布水压,整体说来水位高度变化过程中的溶洞围岩的应力与位移均在增加,但并未出现拉应力；围岩压应力和剪应力均未超过其强度极限,因此可认为溶洞仍是处于较稳定状态。

(4)衬砌后水压增加使弯矩分布变化明显,较大弯矩分布区由边墙部位转移到拱腰部位。工程中,若边墙部位衬砌结构病害整治不及时会导致病害扩散,裂损范围向拱腰部位转移。因此,静水压力引起的结构位移较大,是引起衬砌裂损的主要原因,指明其病害处治的主要任务为衬砌后水压处理。