基于二阶近似积分不等式的时滞系统稳定性分析
2020-09-04龚德仁许光坦段登平
王 楠, 龚德仁, 许光坦, 段登平
(上海交通大学航空航天学院,上海 200240)
时滞系统广泛存在于工业过程、生物、电信、经济、机械工程等诸多实际情况中。系统的时滞往往会引起系统的振荡和不稳定性,这就促使了大量的研究人员致力于用不同的判据进行系统的稳定性分析[1-2]。定常时滞系统稳定性的分析已经得到了广泛的研究,学者们提出了许多理论方法,如特征方程和特征值分析[3-4]。
对于离散时滞系统,早期的学者大多采用离散Jensen不等式[5-6]和自由加权矩阵[7]方法进行稳定性分析。针对线性矩阵不等式(linear matrix inequality,LMI)条件推导过程中存在的二重求和项,文献[8-9]引入了时滞分割方法,文献[10-11]等提出了最优分配方法,使时变时滞系统具有较低的保守性。后来,一些新的方法不断被提出,如有限和不等式[12]、离散Wirtinger不等式[13]以及一些改进的求和不等式[14-18]、凸组合方法[19-20]等。文献[15]建立了基于辅助函数的求和不等式,改进了基于亚伯引理的有限和不等式。文献[20]推导出了改进的凸组合不等式,与扩展的凸组合不等式相比,引入了更少的松弛矩阵变量。
现提出一个新的积分不等式,称为二阶近似积分不等式,著名的Jensen和基于Wirtinger的不等式均为其低阶近似。利用二阶近似积分不等式(SAII)提出具有较低保守性新的时滞系统的稳定性判据,并通过数值算例验证该方法在定常时滞系统中稳定性分析时的有效性和优越性。
1 二阶近似积分不等式


(1)
偏差变量:

(2)

(3)


(4)


(5)


(6)
证明定义如下一系列函数:

(7)
易得:

(8)

(9)

(10)
对t∈[a,b],定义以下函数:


(11)
因为R>0,于是有

(12)
将式(7)~式(11)代入式(12)得:


(13)
至此,可以得到不等式(6)成立,证明完毕。
注1: 将不等式(4)~式(6)右边的项分别定义为

(14)
可以得到:

(15)
结果表明,与Jensen不等式和Wirtinger不等式相比,SAII具有更高的阶近似。实际上,IJensen、IWirtinger和ISAII就是原点二重积分的零、一、二阶近似。证明如下:


(16)
于是有

(17)
将式(17)代入式(3)得:

(18)
式(18)的逆为

(19)



(20)

(21)

(22)

2 定常时滞系统稳定性分析
考虑以下具有区间时变时滞的系统

加拿大各省和美国各州课标中的支股或条目往往不同,连名称都不一样.加拿大西部几省的条目(organizer),包括数的概念(算术),模式与关系(代数),形状与空间(几何),以及概率统计等四项.每一条目下辖若干次级条目.支股也好,条目也好,从一年级引进,不论有无必要,课标中年年出现,直到小学毕业.[9] 传统小学数学自成一个完整有机的体系;而发现式数学基本上是一个若干数学分支的混合.
(23)
式(23)中:x(t)∈Rn表示n维状态向量;A和Ah是具有适当维数的实已知常数矩阵;连续可微函数φ(t)表示初始条件;h≥0是系统的定常时滞。
定理1如果存在矩阵P>0,Q>0和R>0满足式(24)所示条件,则系统[式(23)]是渐进稳定的:

(24)
证明定义如下扩展向量χ(t):

(25)
扩展向量χ(t)可以表示用ξ(t)表示为
χ(t)=Bξ(t)
(26)

(27)
系统[式(23)]可以重写为

(28)
式(28)中:
Ae=[AAh00]
(29)
对χ(t)求导得:

(30)
式(30)中:

(31)
为了分析系统[式(23)]的稳定性,考虑如下李雅普诺夫-克拉索夫斯基泛函(Lyapunov-Krasovskii functional,LKF):


(32)
对Vi(t)求时间导数得到:


(33)
式(33)中:

(34)
证明完毕。
3 算例
算例1考虑具有与文献[21]算例相同系数矩阵的系统式[(23)]:

(35)
使用时滞扫描技术得到最大的时滞上界为hmax=6.172 5。表1给出了本文算法及最近许多使用Jensen不等式、基于Wirtinger的不等式的论文得到的最大允许时滞上界。根据比较结果可知,本文所提出的SAII得到的上界明显优于其他文献。

表1 最大允许时滞上界
算例2考虑在文献[25]中研究的具有如下系数矩阵的动力学:
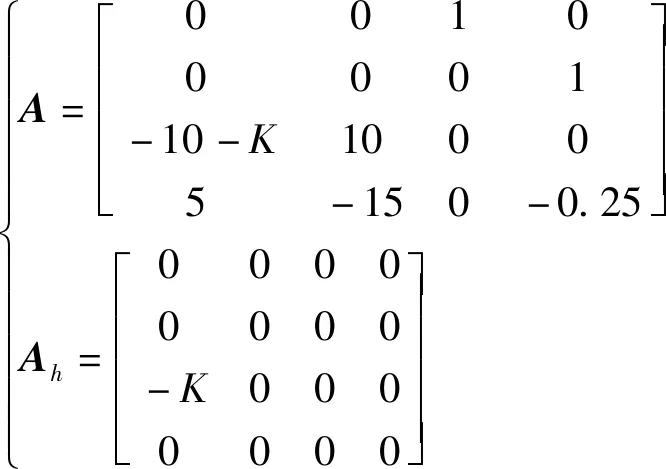
(36)
式(36)中:K为可变参数。
结果表明,与Jensen不等式和基于Wirtinger的不等式相比,SAII的稳定性区域更大,如图1所示。当参数K≤0.295时,即使时滞很大(如h=500时),系统仍然是稳定的。

图1 不同时滞下h的允许上界KFig.1 Allowable upper K with variable delay h
4 结论
提出了一个二阶近似积分不等式(SAII)来分析时滞系统的稳定性,著名的Jensen不等式和Wirtinger不等式均为所提方法的低阶近似。通过选择适当的LKF,引入了新的具有较低保守性的稳定性准则。数值算例表明,与现有的时滞系统相比,该方法有较大的改进。
