基于广义反向学习的改进鲨鱼算法自抗扰参数整定

石春花, 刘 环

(1.长治医学院生物医学工程系,长治 046000；2.长治医学院计算机教学部,长治 046000)

自抗扰控制器是一类不依赖精准数学模型且对外负载扰动具有较强补偿能力的非线性控制器。与传统PID控制、模糊控制等鲁棒控制器所不同的是,自抗扰控制器可将模型内部扰动和外负载扰动归结为总扰动,通过扩张状态观测器对扰动进行观测和补偿。因此针对自抗扰控制器的特点,许多学者将自抗扰控制器应用于各个控制领域中。如无人机控制[1]、四旋翼控制[2]、永磁同步电机控制[3]、微电网无功率控制[4]、雷达伺服系统[5]及风力机变桨控制等[6]。由此可见,自抗扰控制已经应用在越来越多的控制领域当中。但是,非线性自抗扰控制器存在多耦合参数难以优化的问题,很大程度地影响了非线性自抗扰控制器的控制效果。很多学者通过将非线性自抗扰线性化,减少控制参数的方式解决参数难以优化的问题。但当被控对象具有较强非线性或复杂特性时,线性自抗扰难以实现控制目标。因此越来越多的学者对非线性自抗扰参数优化的问题进行了深入的研究。

Guo等[7]提出一种改进粒子群算法的自抗扰参数整定策略,一定程度上提高了控制精度。Yin等[8]提出一种改进的蚁群算法的自抗扰控制器参数整定策略,提高了参数在线优化时间,但控制精度略低。费伦等[9]提出一种变权重变异鸽群优化算法自抗扰参数整定策略。易星等[10]提出一种双种群鲸鱼优化算法的自抗扰参数整定策略,提高了控制精度。周志刚等[11]提出一种基于人群搜索算法的自抗扰参数优化策略,提高了系统响应速度和调节时间。Ge等[12]提出一种基于时间沉降的参数优化策略。以上优化策略均通过提高智能优化算法的全局搜索精度来提对自抗扰参数进行在线优化。但单一提高算法的全局搜索精度难以平衡算法的全局和局部搜索精度,很难快速找到真正的全局最优解。因此本文提出一种改进的鲨鱼优化算法,对自抗扰参数进行在线整定。

针对基本鲨鱼优化算法全局收敛精度不高以及易早熟收敛的问题,通过非线性控制因子,广义反向学习等策略进行改进,平衡改算法的全局、局部搜索能力,提高了算法的整体性能和收敛速度,并将改进的鲨鱼算法用于自抗扰控制参数在线优化,以四旋翼飞行器为被控对象进行仿真实验,对优化后自抗扰控制器的控制精度和抗扰动能力进行验证。

1 自抗扰控制器

自抗扰控制(auto disturbance rejection control, ADRC)控制器主要由三个部分组成。

(1)非线性微分跟踪器(tracking differentiator, TD)安排过渡过程。TD作为一个动态环节,可对急剧变化输入信号进行平滑处理,并有效抑制信号噪声干扰。其数学表达式为

(1)

式(1)中：x1(k)为被跟踪的输入信号；x2(k)为输入信号的微分；T为步长；r为调节因子,对跟踪速率进行调节；h0为滤波因子；fst(·)为快速最优控制综合函数,其数学表达式为

(2)

式(2)中:d=rh0；a的计算公式为

(3)

(2)扩张状态观测器(extended state observer, ESO)将系统模型内部扰动以及外负载扰动综合成一个总扰动,ESO对这个总扰动进行观测和补偿,是可提高自抗扰控制器抗扰动能力的关键组成部分。其数学模型如下:

(4)

式(4)中：y(k)是来自被控制对象的反馈信号；δ为非线性函数的线性宽度；β01、β02和β03为误差校正参数,主要影响建模不确定性和干扰的适应性,是三个待整定参数；z1、z2和z3分别为对x1的估计、x2的估计以及对总扰动的估计；fal(·)函数的数学表达式为

(5)

(3)非线性状态误差反馈率(nonlinear state error feedback control law, NLSEF)。整个系统的干扰在NLSEF中得到补偿,其数学表达式为

(6)

式(6)中：β1和β2为待整定参数，决定控制系统的响应速度。

因此,从式(1)～式(6)中可得,非线性自抗扰控制器待整定参数为β01、β02、β03、β1和β2。

2 改进鲨鱼优化算法

2.1 基本鲨鱼优化算法

鲨鱼优化算法[13](shark smell algorithm, SSA)与传统群智能优化不同,当鲨鱼发现猎物时,会通过螺旋包围的方式对猎物发起攻击。此方式在算法中表现为,算法在寻优过程中,会在接近全局最优解的同时不断扩大包围圈,增加了寻优范围。定义鲨鱼优化算法种群规模为N、维数为D,因此鲨鱼优化算法种群初始化的数学表达式为

Xi,j=[xi,1,xi,2,…,xi,D]

(7)

式(7)中,i=1,2,…,N,Xi,j表示第i个鲨鱼第j个决策变量。此外,鲨鱼在寻找猎物的时候,会不断游向气味更强的猎物,并且随着气味浓度的增加,鲨鱼的速度也会增加。因此,鲨鱼优化算法的速度更新公式可表示为

(8)

式(8)中：j=1,2,…,D；k=1,2,…,kmax为迭代次数；ηk∈[0,1]为速度控制率,为了保证鲨鱼算法在每次迭代过程中的速度均可以达到梯度功能所指示的速度；R1和R2为均匀分布在0～1的随机数,目的是使算法在寻优过程中具有一定的随机性,防止算法过早收敛；OF为目标函数；αk为速度控制率,是0～1的随机数。由于鲨鱼游向猎物的速度为20～80 km,因此定义βk为速度限制率,保证鲨鱼游向猎物的速度在限定范围之内。

鲨鱼向前游动所产生的位置是由先前的速度和位置所决定的,因此鲨鱼优化算法的位置更新公式为

(9)

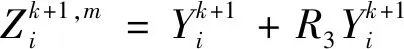
(10)

式(10)中：R3为0～1的随机数,目的使鲨鱼在游向猎物的同时,会在游向路径的周围发起小范围随机性的搜索；m表示鲨鱼算法每次迭代位置更新过程中,螺旋搜索点的个数，并且m个搜索点是相连起来的。如果鲨鱼在向猎物螺旋游动过程中,发现m个搜索点中具有更高的搜索气味,则鲨鱼将改变游动方向,朝具有更高搜索气味的猎物发起攻击。这种行为在算法中可表示为

(11)

2.2 广义反向学习初始化

传统鲨鱼优化算法的种群初始化具有随机性和无规律性,虽然在一定程度上降低了算法的复杂度,但同时在一定程度上降低了初始解的质量,使初始粒子分布不均匀。根据研究表明,当粒子过多的分布在局部最优解的范围内,会导致算法早熟收敛,陷入局部最优,同时会由于初始粒子远离全局最优解,很大程度上降低了算法搜索速度,浪费计算资源。因此针对上诉问题,通过广义反向学习策略,对鲨鱼种群进行初始化。

针对初始化种群的优化算法而言,广义反向学习策略是提高随机优化算法初始解质量的一个重要方法。其主要思想是,计算初始化粒子和其反向点的适应度函数值,并进行贪婪选择。同时为保证在求解反向解时,边界应具有动态变化的特性,以此改变对称中心,达到增强种群多样性,增大初始种群分布范围的目的。反向点求解公式为所示。

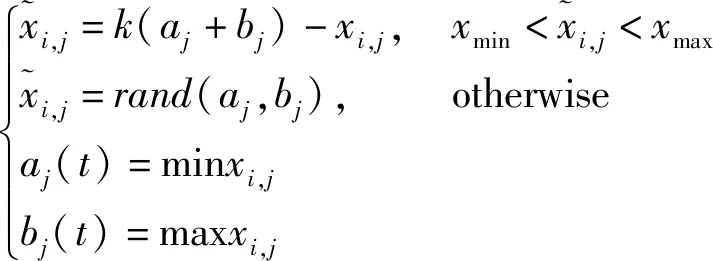
(12)

式(12)中：aj为动态边界的下界；bj为动态边界的上界；xmin为初始解下界；xmax为初始解上界；k=rand(0,1)为动态边界伸缩控制量。与传统反向学习策略相比,广义反向学习策略可让种群的初始分布范围更加广泛,确保全局最优解在可行域范围内,同时加快了算法的搜索速度。其初始化流程如下：

Step 1设种群规模为N,维数为D,并将全部粒子进行初始化xi=(xi,1,xi,2,…,xi,D)。

Step 3计算初始粒子与其对应的广义反向点粒子的适应度值,并进行贪婪选择,淘汰适应度值较差的粒子,保留适应度值较优的粒子,完成种群初始化。

2.3 非线性控制因子

由式(10)可知,控制参数R3主要控制鲨鱼在游动路径发起攻击的攻击范围。在算法中可理解为粒子在寻优过程中,粒子沿当前路径进行搜索时,通过控制参数R3在寻优路径外的范围进行一定规模的随机性搜索,以此在寻优过程中保持种群多样性,提高全局搜索能力。但搜索范围完全依赖随机性,如在迭代后期,搜索随机搜索范围较大,会较大程度影响算法的收敛速度,浪费搜索资源,不利于粒子的局部搜索和收敛。如在迭代前期,搜索范围较小,使得随机搜索范围较小,难以提高算法的种群多样性和全局搜索能力。综上所述,粒子在迭代前期的应具有较大的随机搜索范围,调高算法的全局搜索能力,更可能会将全局最优解覆盖到搜索范围内。粒子在迭代后期应具有较小的随机搜搜范围,可以使粒子在全局最优解附近进行精确搜索,同时提高收敛速度。此外,算法在迭代过程中,全局搜索能力和局部搜索能力的大小应周期性多轮交替,以此达到频繁转变全局搜索能力和局部搜索能力大小的目的。因此控制因子R3应具有周期递减的特性。改进后的R3的数学表达式如式(13)所示。

(13)

式(13)中：φ为频率调节因子,φ越大,搜索范围调节频率越大。由式(13)可知,在迭代前期,R′3的取值较大,随机搜索范围较大。在迭代后期,R′3的取值较小,随机搜索范围较小。因此改进后的位置更新公式为

(14)

2.4 Levy变异

根据研究表明,群智能优化算法在迭代更新过程中,种群中的粒子会不断向当前适应度值较优的粒子靠近,因此当全局最优解距当前种群粒子的距离较远时,由于种群中的粒子向局部最优解靠拢,无法逃逸,算法就会陷入局部最优,早熟收敛。因此,针对上述问题,将Levy变异策略引入算法寻优过程中。Levy变异与二项式变异、混沌变异、柯西变异等传统变异方式的不同之处在于,Levy变异的变异步长远远高于以上传统的变异方式,因此可以给粒子提供的变异范围更广。同时,Levy变异的峰值相较其他传统变异策略的峰值更高,因此可以给粒子提供更强的扰动力,帮助粒子逃逸,跳出局部最优。Levy分布与高斯分布和柯西分布的对比图如图1所示。

图1 三种变异分布对比Fig.1 Comparison of three kinds of variation distribution

Levy变异产生新粒子的数学表达式为

(15)

(16)

由式(15)所知,Levy变异的峰值大小由参数ξ决定,因此,当粒子陷入局部最优时,粒子所获得的最大扰动力也由参数ξ决定。通过大量实验可知,当ξ=2时,Levy变异近似于高斯变异,当ξ=1时,Levy变异近似于柯西变异,经大量实验,选取ξ=0.85,此时Levy变异的峰值最大,范围最广。

2.5 改进鲨鱼优化算法的寻优流程

Step 1初始化种群规模N,维数D,全部粒子进行初始化,并计算初始化个体的广义反向点。

Step 2计算初始粒子与其对应广义反向点粒子的适应度,并进行贪婪选择,完成种群初始化。

Step 3计算初始化后种群中全部个体的适应度值,并进行排序,找出适应度值最小的个体位置作为最优位置。

Step 4依照式(8)、式(14)和式(11)对鲨鱼优化算法的速度和位置进行更新。

Step 5粒子进行Levy变异操作。

Step 6判断是若达到终止条件,是则输出最优个体,即算法找到的最优解；否则,返回Step3。

3 改进鲨鱼优化算法的数值实验

3.1 测试函数选取

为了验证所提改进策略的有效性,选取10个基准测试函数,对GL-SSO算法进行验证,并从全局搜索精度,全局局部搜索平衡能力以及收敛速度等方面对实验结果进行分析。10个测试函数如表1所示。

表1 测试函数

f1～f4为单峰测试函数,f5～f8为多峰测试函数,f9为非连续函数,f10为固定维测试函数。其中单峰测试函数可用于分析算法的收敛速度,多峰测试函数可用于分析算法的全局收敛能力和全局局部搜索的平衡能力。此外为了更加明确地表现所提改进算法GL-SSO的高效性,将GL-SSO的数值实验结果与双种群差分鲨鱼优化算法(DSSO)[14]、自适应反向学习鲨鱼优化算法(ISSO)[15]及均匀变异鲨鱼优化算法(SUSSO)[16]的数值实验结果相对比。其中GL-SSO相关控制参数为ξ=0.85,λ=1.5。其余三种优化算法所需控制参数见相关文献。

3.2 实验结果对比

为保证实验的公平性,在实验时,四种算法的种群规模均为100,维数均为50,实验平台软件硬件均相同。四种算法均实验30次,记录结果的平均值、最小值、标准差,成功率以及平均求解时间。具体结果如表2、表3所示,其中最佳结果用加粗字体表示。

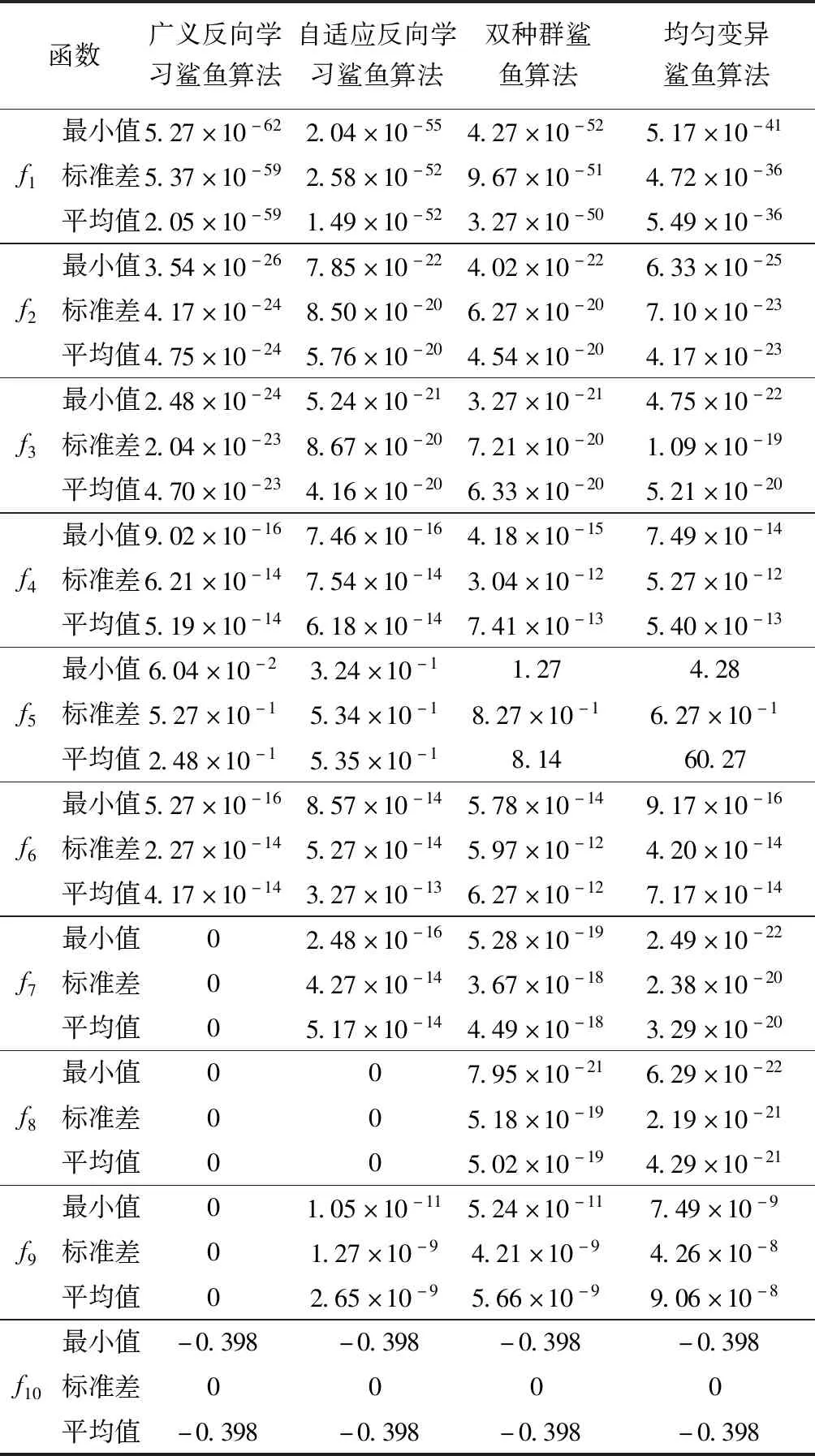
表2 四种算法测试结果比较

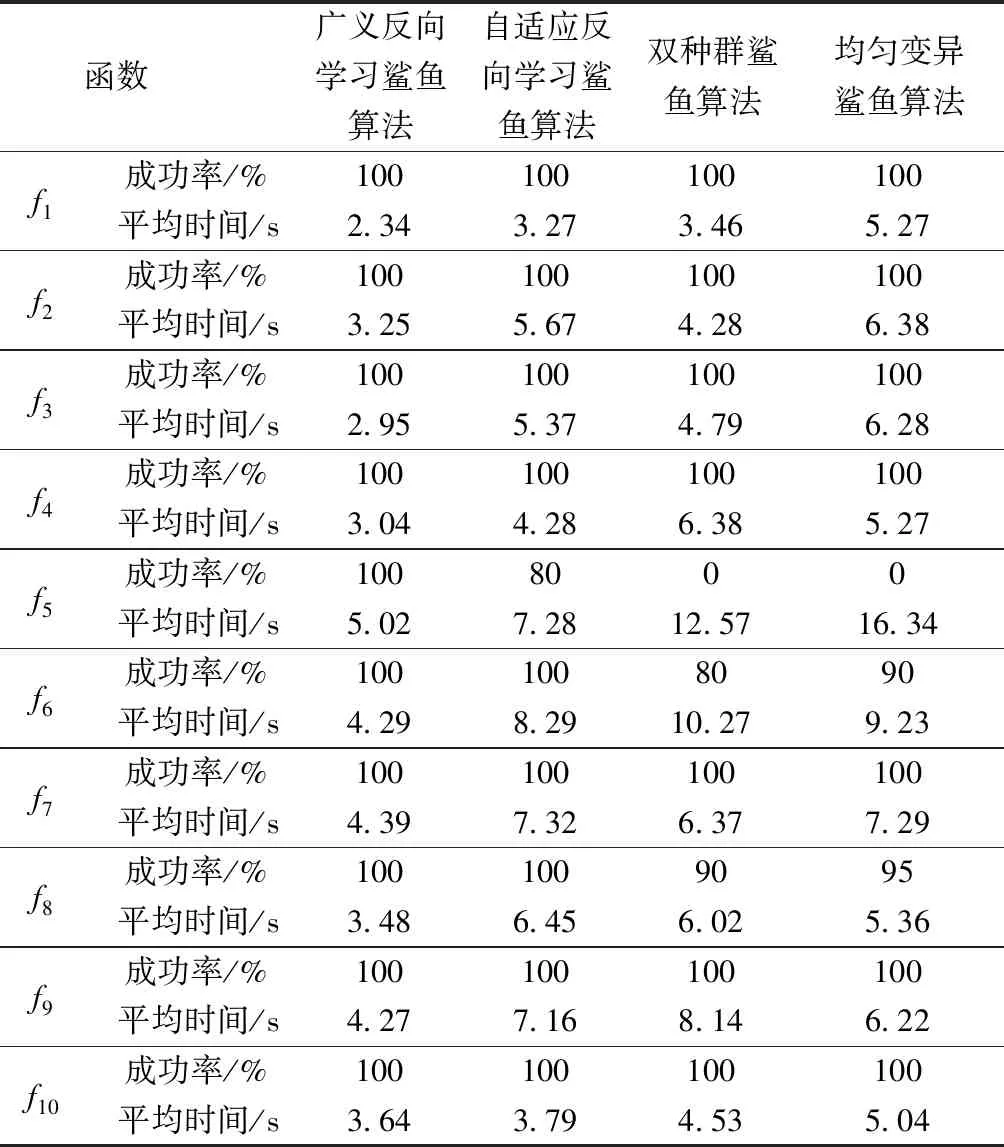
表3 求解成功率与求解平均时间

由表2、表3可知,对于单峰测试函数而言,四种算法均可以求解到最优解,在测试函数f4上,ISSO算法求解的最小值要略高于GL-SSO。但除测试函数f4外,GL-SSO求解的平均值和最小值最小,说明GL-SSO算法的局部搜索能力最强,算法的收敛精度最高,收敛速度最快。其次,GL-SSO求解的标准差要小于其他三种测试函数,说明GL-SSO算法的鲁棒性和稳定性要高于其他三种算法。最后,GL-SSO的求解时间远小于其他三种算法的求解时间,说明GL-SSO算法的收敛速度和种群多样性要强于其他三种优化算法。

对于多峰测试函数f7和f8而言,本文所提GL-SSO算法可以求解到理论最优值,说明相较其他三种算法,GL-SSO算法的全局勘探能力和局部开发能力更为平衡,全局搜索能力较强,种群丰富度更高,这是由于在GL-SSO算法中,控制因子R′3很好地控制了粒子在寻优过程中的随机寻优范围。此外,值得注意的是,对于测试函数f5而言,DSSO算法和SUSSO算法均早熟收敛陷入局部最优,但GL-SSO算法依然可以收敛,求解到最优解,此外,对于全部多峰测试函数而言,GL-SSO算法求解的标准差均最小,说明GL-SSO算法的稳定性更强,不易早熟收敛陷入局部最优,这是由于GL-SSO算法中引入Levy变异的关系,可以当粒子陷入局部最优时,给予较强的扰动,帮助粒子逃逸。同时,对于多峰测试函数而言,GL-SSO的求解时间小于其他三种算法的求解时间,说明GL-SSO算法的收敛速度要强于其他三种优化算法。

对于固定维多峰测试函数而言,四种算法均可以收敛到全局极值,说明当维数较低时,四种算法均具有较强的收敛能力和寻优稳定性。

3.3 时间复杂度对比

对GL-SSO算法的时间复杂度进行反洗。首先,GL-SSO算法主要由广义反向学习,基于周期性递减控制因子的位置更新以及Levy变异组成。设算法的种群规模为100,维数为200。GL-SSO算法的时间复杂度分析如下:广义反向学习的时间复杂度为O(ND),位置更新和速度更新过程的时间复杂度O(ND),Levy变异的时间复杂度为O(ND),因此GL-SSO算法的时间复杂度为O(3ND)。其余ISSO算法、DSSO算法以及SUSSO算法三种优化算法的时间复杂度分别为O(4ND)、O(3ND+2N)、O(4ND),四种算法的时间复杂度为同一量级。

4 实际算例实验

将改进后的鲨鱼优化算法用于非线性自抗扰控制参数在线整定,优化后的自抗扰控制器可记为GL-SSO-ADRC。为了验证GL-SSO-ADRC的控制效果,以四旋翼飞行器为被控对象,对GL-SSO-ADRC的控制精度和抗扰动能力进行验证。由于四旋翼飞行器具有强耦合,非线性的特点,要求控制器应对模型内部扰动具有较强的观测性,对模型的控制响应速度应具有高效性,因此ESO和NLSEF中的误差矫正系数和系统相应控制系数的整定尤为关键。

4.1 四旋翼飞行器数学模型

假设,四旋翼飞行器在地面坐标系下原点相对坐标为Α=[x,y,z],欧拉角为B=[ψ,φ,γ],其中ψ为俯仰角,φ为滚动角,γ为航向角。飞行器的转动角速度为ω=[ω1,ω2,ω3]。因此建立四旋翼飞行器动力学方程:

(17)

4.2 基于GL-SSO-ADRC的四旋翼控制

基于四旋翼动力学方程,构建GL-SSO-ADRC的四旋翼控制流程图如图2所示。

图2 基于改进鲨鱼优化算法的自抗扰四旋翼控制流程Fig.2 Auto disturbance rejection four rotor control flow based on improved shark optimization algorithm

图2中,ITAE为选取的评价指标,算法寻优的终止条件为达到最大迭代次或者ITAE的评价指标值小于等于0.01,若算法达到最大迭代次数时,所求解的全部ITAE均大于0.01,则选取迭代过程中ITAE最小的一组参数,作为ADRC的控制参数。此时应将式(17)更改为自抗扰控制理论相对应的数学表达形式:

(18)

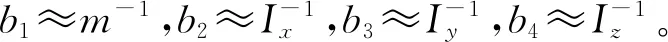
为了验证本文方法的有效性,将GL-SSO、ISSO、DSSO和SUSSO四种算法整定后的自抗扰控制器基于ITAE指标进行对比实验,实验结果如图3所示。可知,相较其他三种算法,GL-SSO-ADRC取得的评价函数ITAE最小,航向角、滚动角及俯仰角的误差均小于0.01,且评价函数值在迭代前期下降速度最快,达到稳态的速度最快,说明相较其他三种算法,GL-SSO-ADRC的寻优速度最快,寻优精度更高。

4.3 实验结果对比

以四旋翼飞行器为被控对象,GL-SSO-ADRC为控制器,在MATLAB2014a中进行仿真实验,其中四旋翼飞行器模型参数如下所述m=1 kg,l=0.24 m,g=9.8 m·s-2,d=1.32×10-6N·s2,b=5.65×10-5m·s-2,Ix=8.25×10-3kg·m2,Iy=8.25×10-3kg·m2,Iz=13.85×10-3kg·m2,J=1.25×10-4kg·m2。整定后的自抗扰控制器参数如表4所示。

为了验证GL-SSO-ADRC的控制效果,分别对航向角、俯仰角、滚动角及飞行高度进行跟踪实验,并将实验结果与ISSO-ADRC、DSSO-ADRC和SUSSO-ADRC的实验结果进行对比,具体结果如下。

4.3.1 飞行高度轨迹跟踪

设飞行器初始高度为0 m,期望高度为2 m,系统输出曲线如图4所示。可知,GL-SSO-ADRC的相对超调量仅为0.08%左右,系统达到稳态时间为0.8 s,ISSO-ADRC的相对超调量为10%,稳态时间为4.3 s,DSSO-ADRC的相对超调量为0.075%,稳态时间为5.6 s,SUSSO-ADRC的相对超调量为15%,稳态时间为6.3 s。在超调量对比上,GL-SSO-ADRC略低于DSSO-ADRC,但到达稳态的时间远远短于DSSO-ADRC的稳态时间。在超调量和达到稳态时间的结果对比上,远远优于ISSO-ADRC和SUSSO-ADRC,可以做到快速无超调的控制目标。

图4 高度及俯仰ITAE对比图 Fig.4 Comparison chart of height track

4.3.2 航向角、俯仰角、滚动角轨迹跟踪

设定航向角初始角度为0°,期望输入为15°增益的周期性方波,输入频率为0.1 Hz。俯仰角和滚动角初始角度为0°,期望输入为30°增益的周期性方波,输入频率为0.1 Hz。为了模拟在实际飞行中受到的噪音扰动,在控制过程中加入白噪声模拟外界负载扰动,系统轨迹跟踪误差如图5所示。

图5 轨迹跟踪误差对比Fig.5 Comparison based on tracking error

从图5(a)中可知,本文所提GL-SSO-ADRC相较其他三种控制算法,跟踪误差精度更高,仅为0.2°,最大误差为0.8°。且系统对外负载扰动的观测和补偿能力更强,受到扰动后,再次达到稳态的时间最短,说明ESO中的误差矫正系数整定的更加合理,GL-SSO-ADRC的控制精度和抗扰动更强。

从图5(b)中可知,加入白噪声扰动后,GL-SSO-ADRC控制的俯仰角最大误差仅为0.2°,在5 s左右基本完全对扰动进行了补偿,相对比其他三种控制算法对外负载扰动的补偿效果更优,系统受到扰动后,使系统达到稳态的时间更短。

同样,从图5(c)中可知,GL-SSO-ADRC的最大误差仅为0.3°,远远小于其他三种控制算法的最大误差。此外,虽然在控制过程中,误差曲线存在波动的现象,这是由于航向角、俯仰角及滚动角之间的耦合关系导致,但GL-SSO-ADRC的误差波动曲线远小于其他三种控制算法,且随时间的增加,GL-SSO-ADRC的控制误差越来越小。

综上所述,GL-SSO算法有效地整定了ADRC的控制参数,提高了ADRC的控制精度和抗扰动能力,同时也提高了ADRC的响应速度。

5 结论

针对非线性自抗扰控制器控制参数难以整定,导致自抗扰控制器控制精度和抗扰动能力降低的问题,提出一种改进的鲨鱼优化算法用于自抗扰控制器参数在线整定。针对传统鲨鱼优化算法全局搜索能力不高以及早熟收敛的问题,通过广义反向学习初始化,Levy变异及周期性递减控制因子加以改进,并通过数值对比仿真实验进行验证了改进策略的有效性。最后以四旋翼飞行器为被控对象,以整定后的自抗扰控制器控制飞行器的飞行高度和欧拉角,进行轨迹跟踪实验,实验结果表明,整定后的自抗扰控制器很大程度地提高了控制器的控制精度和抗扰动能力。