基于三明治夹层约束阻尼结构的潜艇降噪

曾昭阳, 范红伟, 焦映厚，潘 君

(哈尔滨工业大学机电工程学院,哈尔滨 150001)

目前,中国潜艇的静音效果与世界先进潜艇存在较大差距[1]。伴随反潜技术的不断进展,如果噪声得不到高效的控制,就无法满足隐蔽性需求,这对于中国潜艇的发展和技术进步提出了更高的要求[2]。

在潜艇正常航行时,机械噪声是其主要噪声源之一[3]。潜艇机械噪声的形成是由于传动设备和潜艇内的转动装置,在运行的状态下对潜艇形成激励,从而造成自身的振动,并朝着附近区域的水流不断辐射声波。机械噪声的控制及潜艇结构的关联特征,对于潜艇的结构设计提出了更为严格的标准[4]。潜艇是由艇体、设备和传动装置构成的复杂平台,在实际艇身降噪研究中往往做一些忽略和近似。在当代的潜艇设计中,其主体结构通常是通过前后锥壳和处在中间位置的圆柱壳形成,因此在分析潜艇的性能表现时,往往简单处理为回转壳体等几个部分[5],通常的近似方法将艇体近似成厚圆柱壳结构[6]。参考潜艇的大致模型,中外研究人员重点从壳体的振动开始,经过分析厚壳体的振动特征,从而控制振动表现,进而实现潜艇的噪声抑制效果[7-10]。

潜艇在前进的状态下,艇体在面临振源激励作用时将会形成较多的振峰。通过调整结构刚度与密度来解决共振峰问题难以实现,这是由于艇体的厚度与肋板规格大小面临着强度、稳定性的制约。科学家在实践中观察到,通过壳体外层敷设阻尼或者运用阻尼夹层方案可以获得理想的减振效果[11]。在相关材料的刚度较为缺乏时,当整体结构面临着振动问题,这种情况下形成的能量将会很快运动到铺设的阻尼材料中,造成其内部分子链不断运动,彼此摩擦,进而让一定比例的能量转变成热能,所以能够降低板壳的振动[12]。研究人员对于约束阻尼壳体展开了一系列的实验研究,包括阻尼层的阻尼机理及关键影响参数[13],阻尼变形模式影响[14],约束阻尼壳体结构模态阻尼比[15]、声辐射特性[16]等。

“三明治”夹层形式的圆柱壳约束阻尼结构,由于其复合结构形式,可以从几何层面和材料层面进行优化分析设计以提升其振动抑制效果。此次论文重点分析“三明治”夹圆柱壳,研究材料参数与几何参数对壳体模型带来的改变作用,围绕阻尼层的不同参数实施优化,最后将改善后的结果运用在潜艇噪声控制领域,同时明确其降噪效果。

1 约束阻尼层参数对减振效果的影响

“三明治”夹层形式的圆柱壳约束阻尼结构见图1所示,阻尼材料加载基体和约束层之间。当结构产生变形时,在约束层约束下,阻尼层不仅承受拉压变形,还同时承受剪切变形。阻尼层的拉压变形及剪切变形都能起到耗能的作用,且剪切变形其主要作用。阻尼层通常为黏弹性材料。黏弹性材料的重要材料属性之一是其损耗因子。该因子是分析阻尼材料耗散能量能力大小的一个关键指标。损耗因子的定义为

η=ER(w)/Ei(w)

(1)

式(1)中：ER(w)为储存模量；Ei(w)为损耗模量；ER(w)及Ei(w)组成黏弹性材料的复模量[17]

E(w)=ER(w)+iEi(w)=ER(w)(1+iη)

(2)

损耗因子暗示了阻尼材料消耗能量的本领,是材料的固有性质。模态阻尼比为任一阶变形下阻尼材料的消耗能量与存储能量之比,能够反映整体约束阻尼壳结构的结构阻尼特性。随着计算机性能提高,现阶段一般采用模态应变能法计算模态阻尼比[18]。第m阶模态的模态阻尼比这里描述为第m阶模态相匹配的损耗能量和保存的应变能之间的比值结果

(3)

式(3)中：ΔWm为第m阶形式下,阻尼层含有的应变能阐述为；Wm代表第m阶整个结构包含的应变能；η代表相关材料的损耗因子。通过阻尼比的概念阐释能够了解到,在物理层面的含义是在不同的主振型下阻尼材料所包含能量ΔWm在全部变形能Wm中所占的比重,结合两个指标之间的比值能够合理地体现阻尼材料在结构模态中的影响。有限元研究中,可相应地获取任何模态下阻尼单元和整体所包含的变形能,将获取的数值根据所保存的变性能,将获取的数值结果根据既有公式进行运算,进而获取到不同模态下的阻尼比。因此,将以模态阻尼比为评价指标,对圆柱壳约束阻尼结构进行分析研究。

图1 约束阻尼层示意图Fig.1 Schematic diagram of constrained damping layer

为了确定约束阻尼层参数对振动性能 的作用,此次论文中选定足够长度的“三明治”壳体作为分析目标,其1/4模型见图2。

图2 约束阻尼层1/4模型Fig.2 Constrained damping layer 1/4 model

利有限元工具ANSYS,按照一定的方式运算得到所需求的阻尼比参数,因为模型对应为平面应变形式,因此运算过程中使用八节点PLANE183设定尺寸合理的网格。该小节中基体、约束层内部构成都使用的是结构钢,明确其关联参数为:模量E1=210 GPa,泊松比υ1=0.3,密度ρ1=7 800 kg·m-3；初始设定值:E2=2.37(1+i0.5),泊松比υ2=0.42,密度ρ2=999 kg·m-3；其他相关指标的设定值:h2=100 mm。

1.1 损耗因子的作用

复合壳体的截面状态参考图2内容,从内到外不同层的厚度各自对应H1=50 mm、H2=100 mm、H3=50 mm,此时相匹配的半径数值是R1=100 mm、R2=150 mm、R3=250 mm、R4=300 mm。将模型几何规格的保持固定,设定损耗因子分别为0.1、0.2、0.3、0.4、0.5,按照一定次序模型在多个指标数值下完成模态研究,同时获取相应的阻尼比参数,这里以前十阶的阻尼参数为案例,所得结果参考图3。

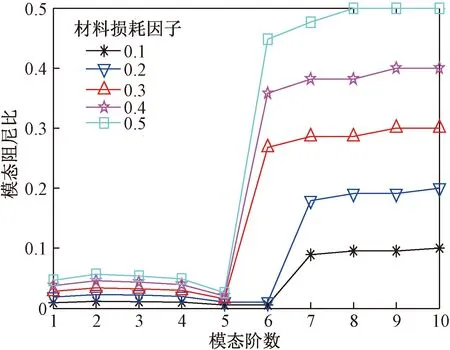
图3 模态阻尼比随材料损耗因子变化规律Fig.3 Variation of modal damping ratio with material loss factor

结合图3的内容能够观察到,此时的前十阶阻尼比浮动规律大体一致,前5阶的指标数值整体不大,而5～7阶出现了一个明显的跃升表现,跃升的最大值就是损耗因子的对应数值。所以,就相关的壳体材料而言,在低频模式下阻尼层具备的作用将会变小,在高频状态下能够实现不错的减振效果。此外能够发现阻尼成分对相应阻尼比数值的影响作用很大,在第7阶后,指标数值保持稳定,跟损耗因子的数值相当,所以选用合理损耗因子的材料十分重要。

1.2 阻尼材料刚度的影响

设定相对刚度为材料刚度和约束层刚度二者之间的比值。考虑到运算的便捷性问题,这里设定材料的泊松比指标为0.3,也就是基体和外部的该指标数值保持一致,模型的结构保持固定,同时对所研究的刚度比设定成1×100、1×10-1、1×10-2、1×10-3、1×10-4、1×10-5,考虑阻尼材料刚度数量级下降时,对阻尼比的影响,即阻尼材料逐渐从高刚度材料转换为柔性类橡胶材料,可以看到材料刚度较低时,阻尼比急剧增加,因此设定上述刚度比。围绕模型不同因素状态下完成相应的模态研究,同时掌握阻尼比数值,运算结果参考图4。

图4 阻尼比和相对刚度的演变规律Fig.4 Evolution of damping ratio and relative stiffness

根据图4,在两个指标之间的变化关系表明,物质的阻尼比跟相应的刚度联系紧密,当后者出现变化时,阻尼比也会很快变化。在相对刚度不超过1×10-3时,约束阻尼层才可发挥预期的减振效果,不然全部壳体结构的前十阶模态阻尼比都非常接近于零,这是因为当刚度数值较大时,整体的振动刚度将会小幅度减小,进而造成阻尼层中消耗热量明显下降；在材料的刚度指标不超过1×10-3时,此时阻尼比的变化规律可总结为:前5阶变化幅度不大,在第5～7阶表现为一个明显跃升,此时跃升的最大值即为损耗因子的数值0.5。所以,就壳体结构来说,阻尼材料的选用需要根据较软材料 的标准来完成。

1.3 阻尼层厚度的影响

有限元分析中,结构从里到外各层厚度分别为H1=50 mm,H2=h,H3=50 mm。阻尼层相应地设定为10、30、50、70、90 mm,该厚度对基体层后续的比值对应为0.2、0.6、1.0、1.4、1.8。让相关的特征参数保持不变,对模型在不同厚度情形下运算其阻尼比指标,此时的运算结果参考图5。

图5 模态阻尼比随阻尼层厚度变化规律Fig.5 The variation of modal damping ratio with the thickness of damping layer

图5分析结果显示伴随阻尼层厚度的改变,壳体的固有频率等均表现为较大幅度的变化。这是由于刚度出现变化后,伴随阻尼层厚度的增加,结构的整体刚度减小,进而造成固有频率减小；就整体的模态阻尼比而言,按照运算结果能够了解到:在阻尼层厚度太小时,此时会让其具备的减振效果无从无发挥,当阻尼层、基体层二者之间的厚度比值超过0.2时,才能发挥应有的减振效果。因此在设计减振结构的过程中,需要合理设定阻尼层厚。

2 圆柱壳体约束阻尼结构减振效果的优化设计

优化设计目的是在阻尼层能量耗散最大化的基础上明确相应的损耗因子、刚度等指标数值。本节将利用 ANSYS 零阶优化算法对一定长度的圆柱壳实施振动优化调整。

2.1 圆柱壳约束阻尼层减振效果优化设计模型

围绕阻尼层结构,经运算和分析后观察到,损耗因子一般在超过第6阶固有频率时才会发挥效果；损耗因子重点影响第7阶之后的昂应指标的最大值；材料的厚度比等因素在所有区间在都会形成作用,在阻尼层和基体层的厚度比值不超过0.2 时,阻尼的功能基本无法发挥,在相对刚度超过 0.2 时,阻尼的价值几乎为零,在相对刚度超过1×10-2时,阻尼材料基本无实际价值。因此在阻尼结构的布置过程中需要使阻尼层与基体层的厚度比H2/H1>0.2 且阻尼层与基体层刚度比G2/G1<1×10-2。优化设计取阻尼各材料参数和阻尼层几何参数为设计变量。表1列出了优化模型的所有优化变量及其上下极限值。

表1 优化变量上下限值Table 1 Upper and lower limits of optimized variables

采用振级落差设定成相应的目标函数,此时运算公式为测量点与激励点在一定频段中最大值的比值结果,重点体现了所有频段中加速度波动的变化状态。

(4)

采用无限长“三明治”壳体模型进行优化分析。无限长特性可以忽略壳体的轴向振动,并取其截面模型进行频率响应分析,平面的变形状态为平面应变。在壳体内部的任何位置添加一定方向的正玄力f=Fsinwt,具体的数值为F=100 N,频率区间是 1～2 000 Hz,其 1/4 截面如图2所示。

基于ANSYS 进行优化设计。第一步借助ANSYSAPDL工具创建所需的分析模型,选取相应的PLANE183设置网络,此时的网格数目达到 886。对内部的任意点进行激励,运算壳体在0～2 000 Hz区间中的响应情况,在ANSYS分析后划定壳体内外层加速度响应,获取内外层全部节点加速度的峰值,借助式(4)运算振级落差, 这样得到优化结果,具体步骤见图6。

图6 优化设计流程图Fig.6 Flow chart of optimum design

2.2 约束阻尼层径向减振效果优的优化结果

优化分析中,相关函数收敛值是1×10-6。科学设定参数的初始值,进行优化后的迭代数值见表2。

表2 设计变量与迭代结果Table 2 Design variables and iteration results

经过12次迭代优化处理,在收敛容差1×10-6区间中设定振级落差的最低数值,此时可形成厚度H2=70 mm,阻尼层刚度为20 MPa,阻尼层材料损耗因子η=0.49时,目标函数Lr的值达到最小值0.12×10-6dB。为明确这对解是否有效,对参数数值进行调整,并完成瞬态分析。接着跟最优解的响应结果对比分析。三个组合的具体参数如表3所示。

表3 不同组合的阻尼层参数Table 3 Damping layer parameters of different combinations

根据表格信息创建所需的模型,对四组对象完成瞬态研究,同时施加一致的外部激励,分析四个测试小组在不同状态参数下的位置、速度等变化,从而充分验证优化结果的精确度。在满足t=1 s时,壳体面临100 N的作用力冲击,四种搭配下的加速衰减如图 7所示。从同一响应点处加速度衰减规律可以看出,相对于无约束阻尼的圆柱壳,阻尼的作用非常明显。优化组合对于调整任何参数的另外组合而言,在相同频率中对应为最低加速度幅值,此时的曲线更为稳定。

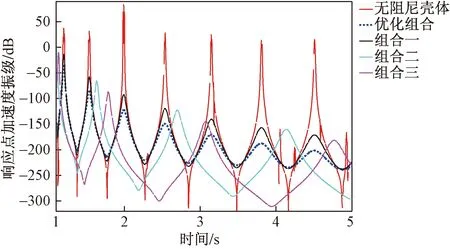
图7 四种不同组合下加速度瞬态响应对数曲线Fig.7 Logarithmic curve of acceleration transient response under four different combinations

3 基于约束阻尼层的潜艇降噪效果

基于 Virtual Lab 软件平台研究阻尼层对潜艇振动的控制效果,同时分析其对声场的作用,并分析约束阻尼层结对潜艇辐射声场的影响规律。

当代潜艇的主体一般划分成三个部分,即头部、尾部与圆柱状中部。所建立的潜艇三维模型[19],研究对象的整体长度为63 m,高7.5 m。借助ANSYS,结合Shell63单元设定密度合理的网络,一共得到523个网格。此时研究中的模型分别如图 8所示。合理设计Shell63的截面属性。单层形态运用为钢材料,具体的参数布置为:弹性模量,E=210 GPa；泊松比为0.3；密度为7 800 kg/m3；厚度H=170 mm。借助相同的方式设计Shell63的截面特征为包含一定阻尼的复合壳体,壳体结构运用2节的减振优化成果,同时设定材料参数为:模量G2=20×106(1+i0.5)Pa,层厚H2=70 mm；壳体层等相应的材料为结构钢,厚度分别为H1=50 mm、H3=50 mm。

图8 潜艇有限元模型Fig.8 Finite element model of submarine

3.1 阻尼层抑制艇体振动效果分析

在潜艇的后部,提供一定的激振力,从而仿真相应设备带来所需的激励效果,此时的频率区间是0～5 000 Hz,具体数值是F=1 000 m·s-2,振源设计见图9。响应点分布在潜艇外部的5点,具体见图9。相应地运算在相同点的激励作用下,阻尼截面与单层截面特征的外层加速响应,同时全面比较。

图9 加速度振源点与潜艇艇体外表面监测点分布Fig.9 Distribution of acceleration vibration source points and monitoring points on submarine external surface

五个监测点在不同的截面属性下加速度振级响应对比结果如图10所示。对比结果表明,在单点正玄激励下,约束阻尼层对潜艇振动具备理想的控制效果。因为内部材料的振动耗能,从而让曲线在高频模式下的峰值被全部清除,在低频模式下的峰值被明显弱化。与单层的曲线比较来说,添加约束作用后,此时的加速曲线起伏更小,更显平稳。

图10 潜艇监测点加速度振级对比Fig.10 Contrast of acceleration vibration levels at submarine monitoring points

3.2 约束阻尼层在降低潜艇辐射声场方面的应用

由振动和噪声的相干性分析知振动的减弱必然造成辐射噪声的减小。本节将研究约束阻尼层在控制辐射声场上的作用。

结合加速度振源对潜艇的激励作用展开仿真,振源等部分的设计规划见图9。此时,振源造成整体振动,进而对周边区域进行辐射,利用Virtual.lab工具围绕声场充分研究。借助Virtual.lab设定水流场的具体参数:密度=1 000 kg·m-3,声速u=1 500 m·s-1。在轴线的相同侧选定5个响应点进行监测。在中部、前侧与后侧分别设定一个监测点,此外在正前位置与后方位置分别设定1个监测点,5个监测点位置见图11。相应地运算两种截面特征下,5个响应点的对应曲线,此时运算结果如图 12所示。

图11 辐射声场响 5 个监测点位置Fig.11 Five monitoring points of radiated sound field

图12 不同截面属性声压响应曲线Fig.12 Sound pressure response curves of different cross-sectional attributes

计算结果说明:运用一致的激励作用形式,在差异性的截面属性下,形成的声场声压具备显著不同；借助一定的阻尼层控制整体的振动,从而减小辐射声场,该方法具备不错的效果。就不包含阻尼层的壳体而言,复合壳体声场声压在0～500 Hz区间中可减小15 dB,在500～2 000 Hz区间中大概可以减小10 dB。

4 结论

基于潜艇减振降噪的需求,研究圆柱壳潜艇简化结构的约束阻尼降噪技术。对“三明治”约束阻尼结构完成参数研究,相应地运算了损耗因子、刚度和层厚度变化时圆柱壳前十阶的模态阻尼比。参数分析结果表明,阻尼材料损耗因子重点影响阻尼比的最大值,在层厚太小及材料刚度太大情况下,都不利于减振效果的发挥。约束阻尼层的厚度与基体层的厚度比应大于0.2,阻尼层刚度与基体层的刚度比应小于0.01。设定相应的目标函数,将损耗因子与层厚等设定成设计变量,结合零阶优化算法实现了约束阻尼层参数的优化。基于阻尼层的优化结果,分析了约束阻尼层在抑制潜艇振动和减弱潜艇辐射声场中的作用。分析结果表明,优化后的“三明治”约束阻尼结构能够使得潜艇在水中的声场声压在 0～500 Hz区间中减小15 dB,在500～2 000 Hz中减小10 dB。