基于数学规划的救援物资分配优化模型及其求解算法综述

曹策俊，高学鸿

（1. 重庆工商大学商务策划学院，重庆400067； 2. 釜山大学工业工程系，釜山609-735，韩国）

0 引言

理论和实践研究表明：救援物资分配问题是应急响应过程中非常重要的研究内容或热点主题［1-3］；制定合理的救援物资分配策略对应急管理的成功具有重要意义［4-5］。主要原因在于：1）van Wassenhove［6］指出应急救援过程中 80% 的活动涉及到物流；且Besiou 等［7］再次全面地强调了人道主义物流活动的重要性。2）Camacho-Vallejo 等［8］指出，实施高效的救援物资分配策略有利于缩短运输时间、减少应急费用以及提高响应效率。3）Hoyos 等［9］明确强调了有效的方法对成功实施救援物资分配方案是必须且重要的，有助于减少死亡人数、财产损失和环境破坏。

此外，Cao 等［1］和 Moreno 等［10］还强调了不合理的救援物资分配策略会导致某些区域严重或相对缺乏物资，可能会诱发各种社会问题，甚至引发极端事件，从而导致应急响应决策系统陷入无序和混乱状态。例如，在2013 年俄克拉荷马州的大龙卷风应对过程中，由于作为救援物资的血液严重缺乏，导致幸存者医疗救助任务开展缓慢，幸存者的痛苦无法得到有效缓解；2015 年北大西洋桑迪飓风毁坏了大量医疗救援物资的预置库存，导致救援工作几乎瘫痪；2018 年印尼地震与海啸响应过程中，由于食物和水的供给不及时，导致诸如抢劫超市和加油站的极端事件发生；在2019 年新型冠状病毒（Corona Virus Disease 2019，COVID-19）事件应对过程中，由于防护口罩等严重缺乏，增加了大众暴露和感染病毒风险。很显然，处理这些问题所需的社会成本会急剧增加。

因此，救援物资在突发事件响应过程中起着至关重要的作用［3］，它是生命延续、应急任务完成的基本保障，缺少救援物资的应急响应没有任何意义。为提高救援物资利用率，缓解幸存者痛苦，以及促进社会、环境和经济可持续发展，如何采用有效方法对救援物资分配优化问题进行建模，设计高效的求解算法，获得最佳分配策略，完成受影响区域涌现出的大量应急任务，从而有效应对大规模突发事件和满足救援过程的可持续要求，是各级决策主体在黄金救援阶段的首要任务之一，也是当前亟待解决的重要课题。

一方面，大规模突发事件的突发性、救援活动本身的高度不确定性和复杂性，增加了救援物资分配优化问题建模的难度。基于此，如何设计有效的方法和算法对救援物资分配优化问题进行建模与求解亟待解决。另一方面，数学规划作为最具代表性的优化方法，许多管理数量方法最终都可转化为数学规划来处理。特别地，2006 年，Altay 等［5］系统梳理了运作研究/管理科学（Operations Research or Management Science，OR/MS）方法在灾害运作管理中的研究现状，强调了数学规划是该领域最受青睐的方法。从这种意义而言，数学规划方法为解决此问题提供了新的思路和技术手段。

数学规划问题的三要素包括目标函数、决策变量和约束条件。该方法被广泛应用于经济、管理和军事等领域。特别地，Galindo 等［11］指出数学规划是对救援物资分配优化问题进行建模的有效方法。基于此，运用数学规划方法对救援物资分配优化问题进行建模是重要且迫切需求的。此外，为了获得救援物资最佳分配策略，还需设计高效的算法求解所构建的数学规划模型。近年来，国内外学者对此主题进行了大量的研究，并取得了丰硕的成果。借鉴文献［12］的观点，为系统梳理和准确识别此领域的研究空白，提出未来研究方向，本文聚焦于数学规划方法在救援物资分配优化问题建模中的应用现状及其求解算法研究现状的梳理和归纳。

具体地，基于系统视角，本文对代表性的相关研究进行全面综述。首先，根据目标数量和“府际”关系两个准则，分别对已有成果进行分类，梳理救援物资分配优化模型的研究现状；接着，阐述求解救援物资分配数学规划模型的精确和启发式算法的研究进展；最后，对数学规划方法在救援物资分配优化问题中的应用及其求解算法研究进展进行总结，并指出未来可能的研究方向。

1 救援物资分配优化模型

正如前文强调的，救援目标的数量、利益相关者间的“府际”关系都会直接影响应急响应过程的整体绩效。基于此，目标（函数）数量、“府际”关系被作为文献分类的准则。因此，首先根据目标函数的数量（即目标数量准则）将已有成果分为单目标和多目标规划模型两类；然后根据利益相关者间的“府际”关系将文献分为考虑横向和纵向“府际”关系两类。

1.1 目标数量准则下的救援物资分配优化模型

目标函数准则下的救援物资分配数学规划模型的一般形式为：

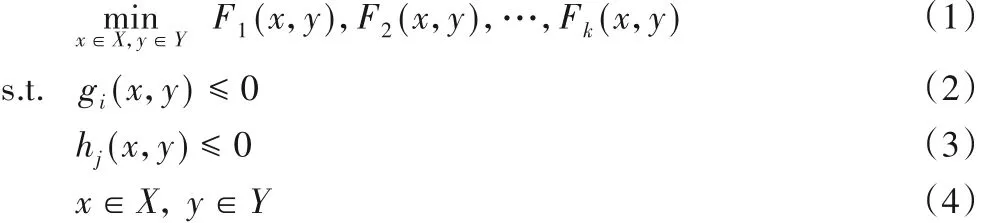
其中：式（1）为目标函数，若k = 1，则为单目标规划模型，否则为多目标规划模型；式（2）、（3）为约束条件，分别为硬约束和软约束；式（4）为决策变量。

针对救援物资分配单目标优化问题，Hwang［13］构建的救援物资单目标分配模型旨在最大限度减少饥饿和痛苦。Fiedrich等［14］建立了以最小化由次生衍生事件、应急救援操作持续时间、缺乏救援行动、延迟运输或转移、运输持续时间内、缺乏转移导致的死亡人数为目标函数的大型救援设备分配模型。Özdamar等［15］、Barbarosoglu 等［16］针对考虑多供应点、同质灾民的救援物资分配问题，分别构建了以未满足需求总和最小、以总成本最小为目标的单目标优化模型。Balcik 等［17］提出的人道主义物流配送单目标规划模型，旨在最小化总成本。Zhang 等［18］针对考虑次生灾害的多供应点应急资源分配问题，构建了以总成本最小为目标的混合整数规划模型。刘亚杰等［19］针对考虑多灾点和公平性原则的选址-分配问题，构建了最大化综合满意度的随机混合整数规划模型。Sheu［20］构建的灾后救援物资服务集中物流分配单目标混合整数规划模型的目标函数为最大化幸存者韧性。王旭坪等［21］提出了以攀比函数值最小化的应急物资分配单目标非线性整数规划模型。Sung 等［22］针对考虑单出救点、异质灾民的应急医疗资源分配问题，提出了以最大化挽救生命能力为目标函数的混合整数非线性规划模型。Li 等［23］聚焦于灾后汽油供应问题，建立了最大化满足度和公平性的混合整数规划模型。Al Theeb等［24］针对考虑异质灾民的车辆路径规划和救援物资分配问题，提出了以最小化未满足需求数量、未接受服务的伤员数量和未转移的工作人员数量为目标函数的单目标整数规划模型。Liu 等［25］针对考虑不确定需求与运输时间的应急物流优化问题，构建了最小化总成本的鲁棒整数规划模型。Liu等［26］针对灾后考虑多品种多阶段的救援物资分配问题，构建了最小化加权未满足需求总和的鲁棒整数规划模型。Sabouhi等［27］针对灾民疏散和救援物资分配集成优化问题，提出了最小化到达时间总和的混合整数规划模型。Zhang 等［28］针对考虑资源再配置的人道主义救援网络设计优化问题，提出了以最小化运输时间总和的分布式鲁棒优化模型。

总体而言，上述研究构建了救援物资分配单目标规划模型，旨在从某个维度实现与时间、成本、死亡人数等相关的单个救援目标。然而，救援物资分配活动涉及多个决策主体，在救援过程中追求的救援目标不尽相同。此外，Holguín-Veras等［29］还强调了多目标优化在人道主义物流中非常受青睐。从这种意义而言，救援物资分配多目标优化问题更贴近实际，且仍需深入研究。

针对救援物资分配多目标优化问题，Cao等［1］构建的救援物资分配多目标混合整数非线性规划模型，旨在最大化最小灾民感知满意度、最小化各需求点感知满意度最大偏差与各阶段感知满意度最大偏差。Moreno 等［10］构建了以最小化物流成本、幸存者痛苦（采用掠夺/偏离成本衡量）的应急物资分配多目标混合整数规划模型。Tzeng 等［30］构建了考虑同质灾民、多需求点与多供应点的救援物资分配多目标整数规划模型，以期实现最小化成本和时间、最大化最小满意度的救援目标。Lin等［31］关注了考虑多车辆、单供应点和可拆分运输策略的关键救援物资分配问题，构建了以最小化未满足需求、运输时间和满意率的差异性为目标函数的多目标整数规划模型。王旭坪等［32］建立了以最大化灾民响应时间、需求和效用感知满意度为目标函数的应急资源分配多目标非线性整数规划模型。王旭坪等［33］还针对多供应点多需求点的应急物资优化调度问题，构建了最小化公众心理风险感知、最小应急物资未满足度的混合整数规划模型。Huang 等［34］建立的救援物资供应公平服务多目标整数规划模型，目标函数为最小化总成本、加权响应时间和不满意需求。Wang 等［35］针对多灾点、多出救点、异质车辆、不充分供应和需求可拆分的救援物资分配问题，构建了开放选址-路径规划非线性整数规划模型，旨在最小化最大路径运输时间和总成本，以及最大化最小路径可靠性。Huang 等［36］构建了以最大化生命挽救效用、最小化延迟成本与需求满足率和理想需求率差的平方和的应急资源运输与分配多目标优化模型。陈莹珍等［37］针对考虑公平性原则、地区自救与互救的多类型多供应点多需求点的应急物资分配问题，构建了应急物资分配多目标整数规划模型，旨在最大化物资需求满足量、最小化最大运输时间。针对考虑多供应点与同质灾民的应急资源调度问题，Mohammadi 等［38］建立了以期望需求覆盖率最大化、总成本最小化和满意率最大偏差最小化为目标的混合整数非线性规划模型；Zhou 等［39］提出了以未满足资源所有类型的数量和运输风险最小化为目标函数的整数规划模型。王雷等［40］提出的应急物流调度多目标非线性整数规划模型，旨在最小化未满足需求、最大到达时间和掠夺成本。Yu 等［41］针对人道主义物流单供应点多需求点资源分配问题，构建了以总成本（包括获得成本、掠夺/偏离成本、惩罚成本）最小为目标函数的整数规划模型。Laguna-Salvadó等［42］针对救援物资采购与分配问题，建立了最大化需求满足度、最小化采购与运输成本、最小化碳排放量、最大化地方投资的多目标整数规划模型。Ghasemi 等［43］针对地震疏散计划中不确定性条件下多目标多品种多阶段多车辆选址-分配优化问题，建立了以最小化总成本和救援物资短缺数量为目标函数的多目标混合整数规划模型。Setiawan 等［44］针对灾后救援物资分配与灾民疏散优化问题，构建了三个数学规划模型，分别为：建立了最小化加权未满足需求数量总和的救援物资分配规划模型；构建了以最小化最大痛苦加权总和与灾区内未疏散受伤灾民痛苦总和为目标函数的灾民疏散规划模型；针对救援物资分配与灾民疏散过程中共用/共享的救援车辆分配优化问题，建立了最小化最大痛苦加权总和与最大痛苦总和的规划模型。

综上所述，表1 梳理了目标准则下数学规划应用于救援物资分配优化问题中的相关文献。特别地，在表1 中，“建模环境”是指研究问题的背景是确定还是不确定（如随机、模糊）环境，是静态还是动态环境。“可持续发展”表示是否明确考虑了可持续发展理念，并将其与数学规划模型联系起来。“目标函数”包括：经济（如成本/费用），社会成本（如公平性、未满足需求），速度（如运输和分配救援物资的时间），挽救生命（如死亡人数、边际效用），环境（如碳排放量）及其他（如风险）。“决策模式”表示在救援物资分配过程中管理者采用的决策模式，包括集中和分散两类，分别用单层、双层/多层规划模型来刻画。

根据表1 可知，已有成果：1）更多地关注与时间、成本、死亡人数相关的单目标函数最优化问题，但较少涉及综合考虑与社会、经济、环境和幸存者等相关的目标函数整体最优的多目标救援物资分配优化问题。2）聚焦于确定环境下的救援物资分配优化问题，或将不确定条件转化为确定环境下的救援物资分配问题来研究，但较少关注不确定（如模糊）环境下的相关问题。3）静态和动态环境下的救援物资分配问题都有所涉及，未发现明显趋势。特别地，救援物资分配动态特征通常可通过离散方式（如多阶段）来刻画，故动态模型可视为多个静态模型在时间维度上的有机结合。在上述文献中，动态建模环境下的应急物流优化问题均属于确定性模型，但极少将动态环境下的相关问题刻画为不确定性模型，原因可能在于尽管不确定性模型更贴近现实情况，但它也更为复杂。4）尽管涉及到了可持续发展理念的某个或两个维度，但并未明确强调与可持续发展的关系，清晰综合考虑社会、经济和环境可持续绩效的文献相对缺乏。5）聚焦于以“供应点-分配中心-需求点”为主线的救援物资分配优化问题，但较少关注“分配中心-需求点-受影响具体区域”分配网络中的相关问题。6）在集中决策模式下，聚焦于考虑同质幸存者的救援物资分配优化问题，但综合考虑多供应点、多需求点、多品种、多车辆、多阶段和异质幸存者的决策优化问题较少涉及。

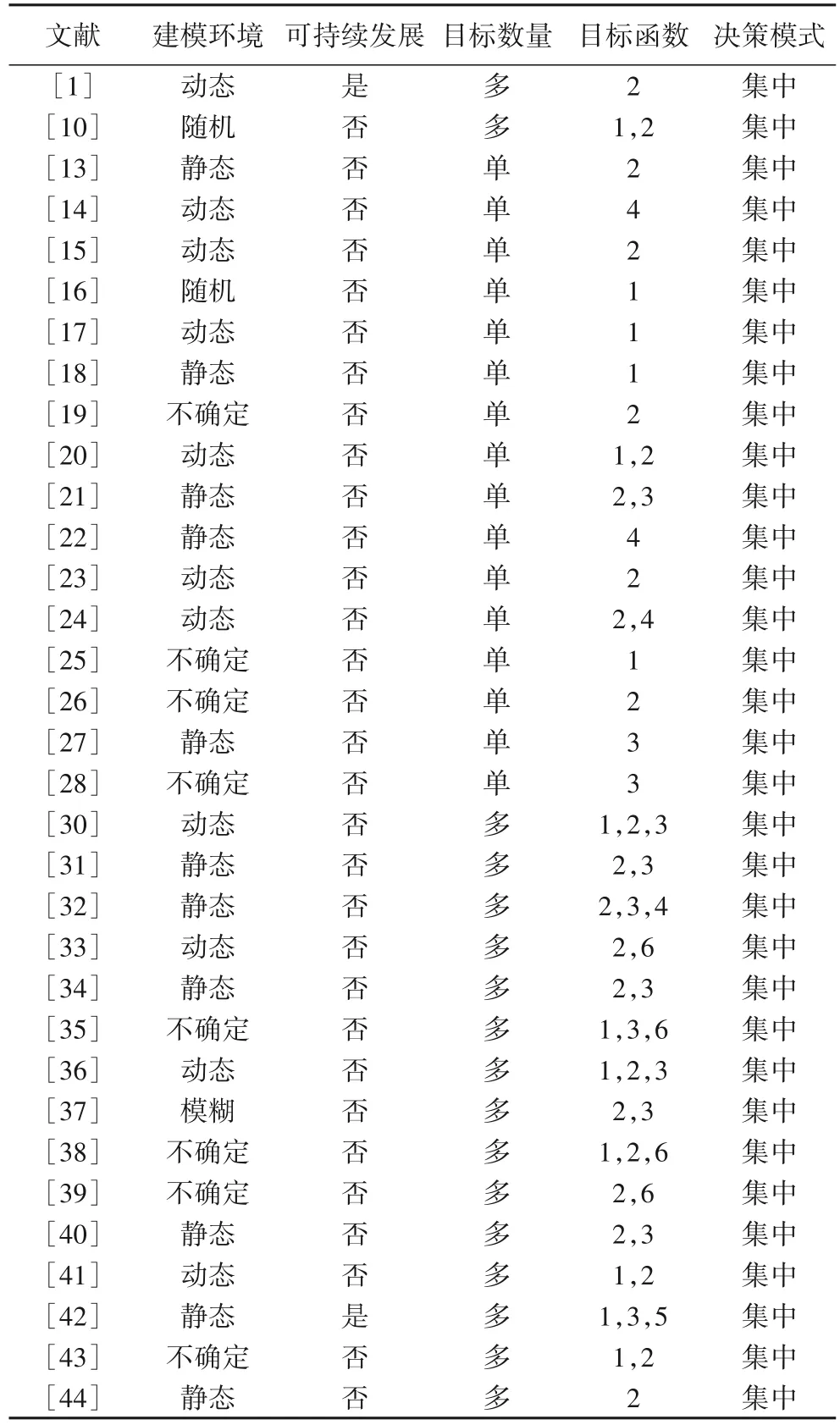
表1 目标准则下救援物资分配文献总结Tab. 1 Summary of the literatures about relief distribution under objective criterion

1.2 “府际”关系准则下的救援物资分配优化模型

曹策俊等［3］强调了“府际”关系是救援物资分配策略制定过程中产生持续作用的关键因素。“府际”关系是指政府间的关系网络，包括横向和纵向“府际”关系两类。具体地，横向“府际”关系是指区域内同层级政府间的关系。横向“府际”关系视角下的决策主体拥有较大的权利，易于快速集中和调度救援物资来应对大规模突发事件，从而控制事件带来的各种影响。将横向“府际”关系考虑到救援物资分配策略中，在很大程度上可有效避免救援过程中出现“打太极”“踢皮球”和“多龙治水”等混乱现象。纵向“府际”关系是指中央、地方与基层等政府间的层级关系。在纵向“府际”关系中，高层级决策主体（起主导作用）对低层级决策主体进行有效控制和领导，低层级决策主体服从领导和接受监督。将纵向“府际”关系融入救援物资分配策略中，既可保证高层级决策主体的权威性，还能调动低层级决策主体的积极性，从而提高响应效率和解决不同层级决策主体间“联动性不足”的问题。此外，“府际”关系准则下的救援物资分配数学规划模型一般形式为：

其中：式（5）和式（7）都是目标函数，若删除式（7），则为横向“府际”关系视角下的单层规划模型，否则为纵向“府际”关系视角下的双层规划模型；式（6）和（8）为各类约束条件；式（9）为决策变量。

针对横向“府际”关系视角下救援物资分配优化问题，文献［1，13-18，20-24，27，30-34，36，40-42，44］针对考虑不同因素的救援物资分配优化问题，分别构建了确定性单层数学规划模型。为了阅读的简洁性，此处不赘述每篇文献的主要工作，可参考第1.1 节。另一方面，文献［10］针对考虑社会成本的应急物资分配优化问题，构建了单层多目标随机混合整数规划模型，以期最优化物流成本和幸存者痛苦。文献［16］采用随机数来刻画需求、供应和能力的不确定性，提出了单层单目标规划模型。文献［19］在考虑震后初期救援阶段对救援物资需求的不确定性和应急救援环境的特殊性的基础上，建立了单层随机混合整数规划模型。文献［25-26］在考虑需求和运输时间不确定性的基础上，提出了单层鲁棒整数规划模型。文献［28］将需求、运输时间、货运不确定性因素考虑到人道主义救援网络优化设计问题中，建立了单层单目标鲁棒优化模型。文献［35］运用可靠性来刻画不确定性，构建了救援物资分配单层多目标非线性规划模型。文献［37］关注了考虑模糊需求和公平原则的应急物资分配问题，建立了单层多目标模糊整数规划模型。文献［38］考虑了需求与运输成本不确定性因素，提出了救援物资分配单层多目标随机非线性整数规划模型。文献［39］将路网不确定性因素融入应急资源动态调度问题中，建立了多阶段整数规划模型。文献［43］考虑了地震疏散计划中地震发生、避难场所和医疗中心失效的不确定性因素，建立了多阶段单层混合整数规划模型。此外，感兴趣的读者还可参考文献［5，11，45-46］。

总体而言，上述文献仅仅关注了在救援物资分配过程中，同层级不同部门决策主体的救援目标。然而，在大规模突发事件应对过程中，救援物资分配活动相当复杂，涉及的多个决策主体间除了存在横向“府际”关系，还有层级或主从或纵向“府际”关系（如中央、地方和基层政府），且这些主体都有各自的救援目标。在救援物资分配策略制定过程中，需要适当地考虑或平衡纵向“府际”关系视角下的不同目标。

针对纵向“府际”关系视角下救援物资分配优化问题，在确定条件下，Camacho-Vallejo 等［8］构建的救援物资分配双层整数规划模型中，上层决策旨在最小化救援物资运输总的响应时间，下层决策旨在最小化从其他国家和国际救援组织的运输成本。Kongsomsaksakul 等［47］构建了大规模洪涝灾害后避难所选址的双层规划模型，上层决策目标为最小化疏散时间总和，下层决策目标为最小化灾民到避难所最少耗费时间。王苏生等［48］针对多灾点拥挤资源竞争和分配不均问题，构建了考虑及时性和公平性的双层规划模型。Duan 等［49］将应急救援响应和车辆总花费时间、未满足需求惩罚作为上层决策的目标，将车辆再分配所耗费的时间作为下层决策的目标，进而构建应急车辆分配与再分配的双层规划模型。Gutjahr等［50］聚焦于人道主义物流救援物资分配中心选址问题，构建了双目标双层规划模型，在上层决策中考虑了决策者最大化覆盖率和最小化建设成本的优化问题，在下层决策中考虑用户均衡因素。郑斌等［51］针对震后多运输方式的应急物流选址-联运问题，构建了上层最大化物资运送时间满意度，下层最大化物资分配公平性的双层规划动态模型。Chen 等［52］针对多供应点多需求点救援物资分配问题，构建了上层最小化加权分配时间，下层最大化分配公平性的双层0-1 整数规划模型。刘长石等［53］针对考虑公平和效率因素、受灾群众的非理性攀比心理的应急物资分配与运输问题，构建了上层最小化所有需求点的损失攀比效应总和，下层最小化物资运达需求点的时间攀比效应总和、总运输时间的混合整数规划模型。

在不确定条件下，陈刚等［54］针对考虑模糊需求的应急物资配送中心与集散点选址以及车辆路径规划问题，建立了上层以最小化最晚运达时间、最小化配送总成本与最大化车辆载重利用率为目标，下层以运输总成本最小为目标的0-1 整数双层规划模型。Safaei 等［55］针对需求和供应不确定的多供应多需求点救援物资供应-分配问题，提出了鲁棒双层整数规划模型，上层最小化救援活动总成本，下层最小化供应风险总和。Safaei 等［56］还针对考虑需求不确定性和供应风险的应急物流规划问题，构建了上层以最小化未满足需求总和与总成本为目标函数，下层以最小化供应风险总和为目标函数的救援物资分配双层双目标整数规划模型。曹策俊等［57］在考虑分配网络中不确定供应、需求和行程时间、公平分配原则等特征基础上，构建了上层最小化加权行程时间总和、下层最大化加权感知满意度的双层整数规划模型。Gao［58］针对考虑不确定需求和运输网络可利用性的多种类救援物资再分配问题，建立了双层随机混合整数非线性规划模型，上层优化问题最小化不满意水平总和，下层问题最小化期望运输时间总和。Li等［59］针对灾后多阶段应急资源（包括道路修复人员与救援物资）动态联合配置问题，构建了上层最大化累计可达性，下层最小化总运输时间和最大化救援物资分配公平性的双层整数规划模型。Kamyabniya等［60］针对人道主义救援中不确定条件下血小板物流规划问题，构建了两阶段数学规划模型：第1 阶段建立了上层最小化总运输时间、下层最小化总运作成本的模糊混合双层整数规划模型；第2 阶段设计了能力共享机制改善第1 阶段的结果。此外，感兴趣的读者还可参考文献［61-63］。

综上所述，表2 梳理了纵向“府际”关系准则下数学规划应用于救援物资分配优化问题中的相关文献，而横向“府际”关系视角下的相关文献见表1。在表2中，“上层目标函数”和“下层目标函数”分别表示上层和下层优化问题的目标函数；其他列所表示的含义与表1中的相同。

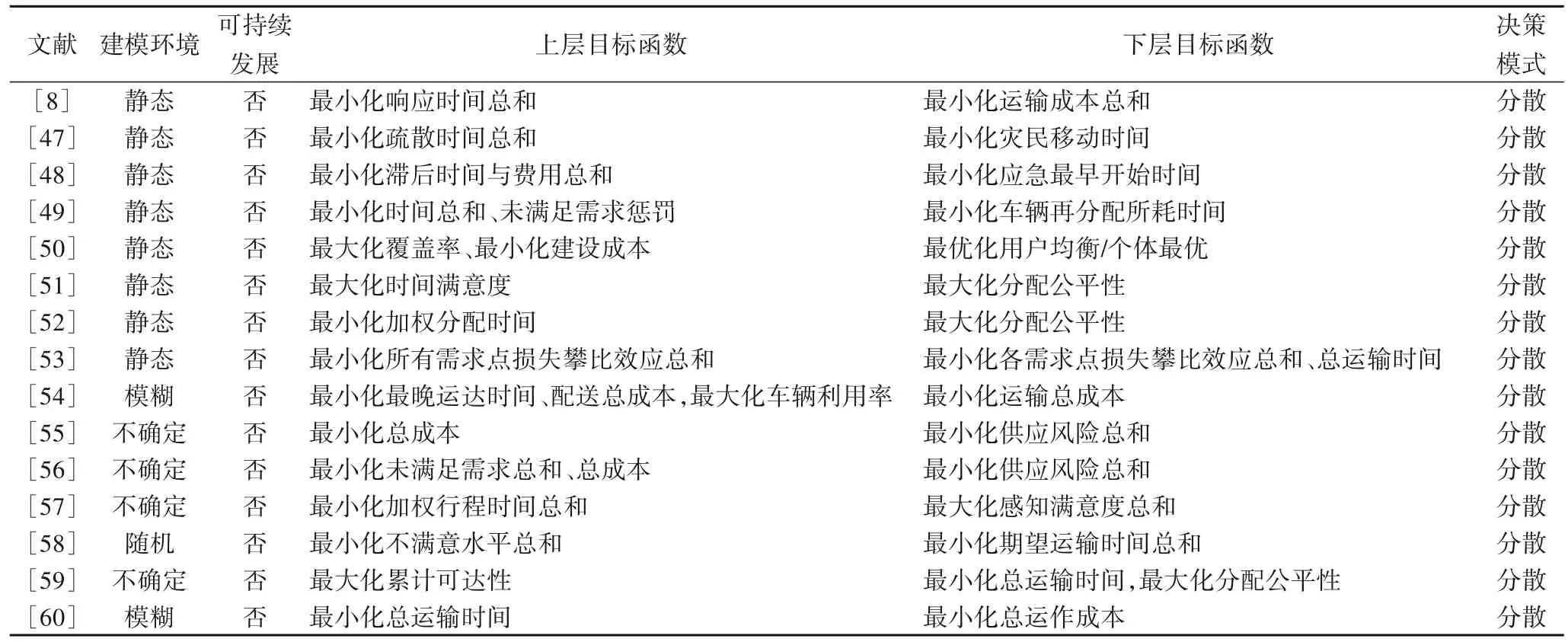
表2 纵向“府际”关系准则下救援物资分配文献总结Tab. 2 Summary of the literatures about relief distribution under vertical intergovernmental relationship criterion

根据表1、2 可知，大部分学者：1）侧重于从横向“府际”关系视角解决同层级决策主体或不同部门在不同维度利益诉求的冲突问题，但较少从纵向“府际”关系视角关注如何平衡不同层级利益相关者在不同方面的利益诉求问题。2）更多地聚焦于纵向“府际”关系视角下静态救援物资分配问题，但较少探索动态的救援物资双层优化问题。3）聚焦于构建确定环境下考虑纵向“府际”关系的救援物资分配问题，但较少涉及不确定性环境下的相关问题。4）将静态与动态、确定与不确定建模环境分别孤立考虑，但如何将两个维度综合交叉考虑需进一步探索。特别地，将不确定性因素与动态特征综合考虑到救援物资双层优化问题中的成果极少，这与横向“府际”关系视角下的结论是一致的。5）关注传统视角下考虑纵向“府际”关系的救援物资分配优化问题，但极少从可持续发展视角研究相关问题（与1.1 节得到的结论相似）。6）在分散决策模式下聚焦于研究考虑同质幸存者的分配中心选址、车辆调度、路径规划等问题，但未融入“以人为本”的理念，未考虑异质幸存者的救援物资跨区域分配双层优化问题。7）建立了上层单目标、下层单目标的救援物资双层规划模型，且追求与成本、时间相关的救援目标，但较少构建上层多目标、下层单目标的双层规划模型。

1.3 救援物资分配模型的比较分析

尽管上述内容已从目标数量和“府际”关系两个准则对救援物资分配数学规划模型进行了分类，但仍较少涉及模型本身以及模型间的异同点。本节拟根据决策因素对已有的救援物资分配模型进行比较。特别地，决策因素是指在构建救援物资分配模型时需要考虑的影响因素。诸如建模环境、利益相关者间的“府际”关系、救援目标的数量等这类决策因素会直接影响分配模型的性质和求解难度，而诸如物资种类、供应点与需求点的数量、幸存者的异质性、运输工具的数量等这类决策因素更多地直接影响仿真结果（即救援物资分配满意方案）。另外，决策因素的个数在某种程度上体现了所构建模型对现实问题的抽象程度。通常情况下，模型中考虑的决策因素越多（少），表明其越接近（远离）现实世界。在应急管理实践中，数学规划模型是现实案例的抽象。一方面，决策主体希望所构建模型能够尽可能完美地刻画现实案例，增加其适用性；另一方面，决策主体也希望能在尽可能短的时间内获得分配方案，提高其时效性。这就要求所构建的模型复杂度不能太高，否则求解所耗时间或很长，甚至找不到满意解。因此，在构建救援物资分配数学规划模型时，需要综合考虑模型的适用性与复杂性。

总体而言，在已有成果中，救援物资分配模型可以分为以下几大类：确定性与不确定性、单层与多层、单目标与多目标、静态与动态规划模型。

就确定性与不确定性救援物资分配规划模型而言，区别在于：前者的决策环境是已知的或可完全估计/预测的，而后者的决策环境是不能完全估计/预测的。例如，文献［1，8，13-18，20-24，27，30-34，36，40-42，44，47-53］构建的决策模型属于确定性救援物资分配模型，而文献［10，16，19，25-26，28，35，37-39，43，54-60］建立的决策模型是不确定性分配模型。

就单层与多层救援物资分配规划模型而言，区别在于：在方案制定过程中，前者的决策主体属于同一层级，而后者属于不同层级，具有主从关系。例如，文献［1，10，13-28，30-44］提出的分配模型是单层规划模型，而文献［8，47-60］所建立的决策模型是双层规划模型。

就单目标与多目标救援物资分配规划模型而言，区别在于：前者的决策主体仅仅考虑单个救援目标，而后者需要同时考虑至少两个救援目标。例如，文献［13-28］构建了救援物资分配单目标规划模型，而文献［1，8，10，30-44，47-60］建立了救援物资分配多目标规划模型。

2 救援物资分配数学规划模型求解算法

在大规模突发事件应急管理实践中，为了向决策主体提供更为精确和针对性的决策支持，除需要依靠第1 章讨论的各类数学规划模型，还必须借助各类技术手段和工具来求解这些模型。为了应对大规模突发事件背景下救援物资分配优化问题与模型的高度不确定性、随机性、复杂性，如何设计合理且高效的求解算法是应急管理的主要任务之一。

诸如 Cao 等［1］、Anaya-Arenas 等［4］和 Lu 等［61］学者指出求解应急资源配置模型的技术手段可分为精确算法和启发式算法两类。借鉴上述观点，将求解救援物资分配数学规划模型的方法也分为精确算法和启发式算法。前者主要适用于救援物资分配优化小规模问题，包括分支定界法、原始-对偶算法等；后者主要适用于大规模问题，包括遗传算法、模拟植物生长算法、差分进化算法等。特别地，问题规模大小的界定并没有严格的统一标准，在实际问题中一般视情况而定。在黄金救援阶段，由于可利用的救援物资的稀缺性，救援物资分配中心、救援物资数量相对较少。然而，在大规模突发事件背景下，应急需求点、应急任务的数量都相对较多。

2.1 求解救援物资分配模型的精确算法

近年来，有学者运用诸如分支定界法、原始-对偶算法、CPLEX 软件等精确算法或内置精确算法的软件求解相对简单的救援物资分配数学规划模型。例如，Barbarosoglu 等［16］运用通用代数建模系统（the General Algebraic Modeling System，GAMS）软件求解了救援物资分配单层单目标规划模型。Balcik 等［17］借助 GAMS/CPLEX 软件求解了人道主义物流配送规划模型。Sheu［20］运用实证和精确算法对灾后救援物资服务集中物流分配单目标混合整数规划模型进行了求解。Sung等［22］采用列生成法求解了应急医疗资源分配混合整数非线性规划模型。Li 等［23］和 Huang 等［34］分别运用 CPLEX 软件求解了灾后汽油供应分配混合整数规划模型、救援物资供应公平服务整数规划模型。Liu 等［25］与 Zhang 等［28］借助 CPLEX 软件分别求解了应急物流分配（再分配）鲁棒整数规划模型。Liu等［26］设计了基于鲁棒预测控制和滚动窗口的框架，求解灾后救援物资分配鲁棒整数规划模型。Tzeng 等［30］采用融入模糊逻辑思想的规划方法对救援物资分配多目标整数规划模型进行了求解。Yu 等［41］设计了动态规划算法求解人道主义物流资源配置规划模型，与循环运输法相比较，该算法在求解效率方面具有显著优势。Laguna-Salvadó 等［42］针对可持续救援物资采购与分配整数规划模型，提出了层次优化方法。Gutjahr等［50］针对救援物资分配中心选址双层双目标优化模型，提出了包括ε-约束、分支定界法和Frank-Wolfe 的精确算法对其进行求解。Camacho-Vallejo 等［8］针对救援物资分配双层整数线性规划模型，设计了以互补松弛条件为基础的原始-对偶算法。在文献［8］的基础上，Safaei 等［55］将其运用于求解不确定条件下救援物资供应-分配鲁棒双层优化模型，而曹策俊等［57］将其运用于求解救援物资跨区域分配双层整数规划模型。Safaei 等［56］采用目标规划方法求解了应急物流规划双层双目标整数规划模型。Gao［58］采用CPLEX 软件求解了救援物资再分配双层随机混合整数非线性规划模型。Kamyabniya等［60］提出了K-best算法求解血小板应急物流计划模糊混合双层整数规划模型。通过梳理上述文献发现，文献［8，16-17，20，22-23，25-26，28，30，34，41-42，50，55-58，60］通过设计/考虑不同情景或视角，验证了所设计算法在不同性能指标方面的潜在优势。

总体而言，上述成果针对救援物资分配数学规划模型，设计了不同的精确算法来获得最优分配方案。然而，在大规模突发事件背景下，救援物资分配优化问题具有高复杂性和不确定性等特征，具体表现为多类型资源、多层级关系、多救援目标、多约束条件等的交叉关联性。因此，在有限时间内，采用这些精确算法，很难找到此类问题的最优解。并且，随着问题规模逐渐增大，精确算法的局限性更加凸显，增加了获得最优解甚至可行解的难度。基于此，需要引入启发式算法来解决此问题。

2.2 求解救援物资分配模型的启发式算法

为了克服精确算法的局限性，学者们尝试采用诸如遗传算法、模拟植物生长算法、差分进化算法等启发式算法求解相对复杂的救援物资分配数学规划模型。Cao 等［1］建立了可持续救援物资分配混合整数非线性规划模型，提出了采用十进制矩阵编码的遗传算法求解此模型。仿真结果表明：满意分配方案可在20 min 内获得，体现了所设计算法的高效性。Moreno 等［10］设计了固定-优化、两步启发式算法求解应急物资分配随机混合整数规划模型，与其他不同求解策略下不同算例的仿真结果相比，其所设计算法具有良好的性能。Hwang［13］提出了遗传算法和混合动态算法求解救援物资分配模型，并以朝鲜饥荒救援食物供应链为例验证了所设计算法的潜在优势。Fiedrich 等［14］采用模拟退火与禁忌搜索算法求解了大型救援设备分配模型，并通过算例结果比较验证了所提出的算法在性能指标方面的优越性。Özdamar 等［15］提出了基于拉格朗日松弛法的迭代算法求解救援物资分配单目标优化模型，并利用小规模算例与实际地震案例验证了所设计算法的收敛性。Zhang 等［18］设计了启发式算法求解考虑次生灾害的多供应点应急资源分配混合整数规划模型，并通过与分支定界法进行对比，验证了该求解算法在目标函数值和计算时间方面的优越性。刘亚杰等［19］设计了基于拉格朗日松弛的快速算法求解救援物资选址-分配随机混合整数规划模型，而且与CPLEX 软件的求解结果进行比较的结果表明，该算法在求解效率和质量方面具有潜在优势。2005 年，李彤等［64］首次正式提出了模拟植物生长算法。王旭坪等［21］将其运用于求解应急物资分配非线性整数规划模型，与遗传算法的比较结果验证了该算法的优越性。Al Theeb 等［24］设计了启发式算法/框架对人道主义物流中车辆路径规划和救援物资分配整数规划模型进行求解，并通过与商业软件的求解结果进行比较，验证了所提出的算法具有较强的优越性。Sabouhi 等［27］提出了文化基因算法求解灾民疏散与救援物资分配集成优化混合整数规划模型，通过车辆数量和避难场所的容纳能力两个维度，验证了所设计算法的有效性。Lin 等［31］设计了遗传算法求解灾后关键救援物资分配混合整数规划模型，而且与分配与分解算法等方法的仿真结果进行比较，结果表明所提出的启发式算法在不同问题规模中都具有潜在的优势。王旭坪等［32］针对应急资源分配非线性整数规划模型，采用了包括主要目标法、分层排序法、分散搜索算法在内的启发式算法对其进行求解，并通过算例证明了其有效性。王旭坪等［33］还采用了包含遗传算法的多层搜索算法对应急物资优化调度混合整数规划模型进行求解，并通过与未考虑公众风险感知的仿真结果相比较，验证了所设计算法的有效性。Wang等［35］设计了带精英策略的非支配排序遗传算法和差分演化算法对救援物资分配非线性整数规划模型，并通过汶川特大地震的算例验证了该算法在性能指标上的优越性。Huang 等［36］设计了差分不等式算法求解应急资源运输与分配优化模型，实验结果表明，随着问题规模的不断增大，该算法仍能表现出较强的优势。陈莹珍等［37］设计了改进差分进化算法求解应急物资分配整数规划模型，通过不同算例验证了该算法对大规模问题的有效性。Mohammadi等［38］针对震后应急物资供应混合整数非线性规划模型，提出了多目标粒子群优化算法，通过与修正时间变量的多目标粒子群算法、带精英策略的非支配排序遗传算法等求解方法获得的仿真结果相比，所设计算法更优。Zhou 等［39］提出了基于分解的演化算法求解多阶段动态应急资源调度整数规划模型，与带精英策略的非支配排序遗传算法相比，该算法获得的满意解较优。王雷等［40］运用带精英策略的非支配排序遗传算法求解了应急物资分配非线性规划模型，并通过比较不同应急策略下的结果验证了该算法的高效性。Ghasemi等［43］针对震后选址-分配混合整数规划模型，提出了多目标粒子群算法对其进行求解，并通过与ε-约束、带精英策略的非支配排序遗传算法的比较，验证了所设计算法在求解质量和求解效率方面具有较强优势。Setiawan 等［44］提出了基于v-长度和4 个点的启发式算法求解救援物资分配与灾民疏散数学规划模型，并通过大规模与小规模算例的仿真结果验证了所设计的求解策略的高效性。Kongsomsaksakul 等［47］针对避难场所选址与分配双层整数规划模型，设计了嵌套式遗传算法对其进行求解，并从不同维度验证了算法的有效性。王苏生等［48］设计了动态优选策略求解应急资源配置双层规划模型，实验结果表明该策略可以获得全局最优分配方案。Duan等［49］设计了双层混合蛙跳算法求解应急车辆分配与再分配双层整数规划模型，并通过与双层粒子群算法的仿真结果进行比较，验证了该算法在求解质量和求解效率性能指标上的优越性。郑斌等［51］提出了混合遗传算法求解应急物流动态选址-联运混合整数双层规划模型，仿真结果表明该模型获得满意运输方案的时间不超过20 min，所设计的算法效率较高。Chen 等［52］设计了改进差分演化算法求解自然灾害救援物资供应配置双层规划模型，并通过与其他差分演化算法的比较结果验证了该算法的高效。刘长石等［53］提出了混合遗传算法求解应急物资分配-运输双层协同优化模型，能在5 min 内获得满意方案，表明该算法具有较高的求解效率。陈刚等［54］等运用自适应遗传算法求解了应急物资配送中心、集散点选址与路径规划0-1 整数双层规划模型，且通过与传统遗传算法的比较验证了该算法在效率指标方面的优越性。Li等［59］设计了稳态并行遗传算法求解应急资源动态联合配置双层整数规划模型，并从不同视角验证了该算法能在合理的计算时间内获得较高质量的满意解。

2.3 救援物资分配模型求解算法存在的问题

综上所述，表3 梳理了救援物资分配数学规划模型求解算法的相关文献。在表3 中，“求解算法/工具”表示文献采用的具体求解方法或技术手段，可包括遗传算法、模拟植物生长算法、差分进化算法、模拟退火算法、禁忌搜索算法，分支定界、动态规划算法、原始-对偶算法、ε-约束、软件求解器（如GAMS、CPLEX）等；“算法类别”包括精确算法和启发式算法两类。

根据表3 可知，大多数学者：1）在精确算法方面，更多地借助CPLEX 或GAMS 等软件的内置算法求解救援物资分配数学规划模型。特别地，针对双层规划模型，通常采用原始-对偶算法、塔克-库恩条件将双层转化为单层规划模型进行求解。2）在启发式算法方面，聚焦于运用遗传算法、粒子群算法、差分进化算法、模拟植物生长算法及其衍生算法等求解所构建的救援物资分配数学规划模型。3）与精确算法相比，无论是针对救援物资分配单层规划模型还是双层（或多层）规划模型，诸如遗传算法的启发式算法在求解过程中更受青睐。4）聚焦于将精确算法与启发式算法应用于求解救援物资分配单层单目标或多目标规划模型，但较少将其用于求解救援物资分配双层规划模型。基于此，如何设计支持“多准则决策建模、高不确定性和复杂性求解”的高效率启发式算法求解救援物资分配模型，仍需深入研究。

在采用精确算法与启发式算法求解救援物资分配优化问题的相关文献中，文献［1，10，13-28，30-44］设计的算法适用于求解单层数学规划模型。文献［8，47-60］所提出算法的适用范围为双层数学规划模型；其中，文献［8，47-53］所设计算法的适用范围为确定性数学规划模型，文献［54-60］提出的算法适用于求解不确定性救援物资分配模型。此外，所设计的精确算法或采用的求解器更多地适用于小规模分配问题，所提出的启发式算法在求解大规模分配问题时，其潜在优势更明显。

特别地，本文所涉及的文献主要设计了遗传算法、模拟植物生长算法、进化算法等，在设计新的求解算法时，应该从收敛性、收敛速度、适用范围等方面来考虑。原因在于：第一，收敛性体现了算法的搜索深度，也决定了所获得满意解与最优解间的距离。在应急管理实践中，较差的救援物资分配方案会给社会带来更多的问题。第二，收敛速度决定了在有限时间内获得满意解所需的时间。时效性是大规模突发事件救援物资分配优化问题的典型特征，决策主体制定策略的时间越短，越有助于提高整体救援效果/绩效。第三，救援物资分配优化问题具有典型的层级或主从关系，这要求所设计求解策略也需要考虑该特征。因此，将求解单层规划模型的算法拓展为求解双层甚至多层规划模型的嵌套式算法，从而提高算法的适用范围，是当前亟待解决的问题。第四，国内外学者更多地将所设计算法与其他算法的仿真结果进行比较，较少将已有算法与其他典型的算法相结合，构造出具有特色并适用的多方法集成算法以解决更复杂的救援物资分配优化问题，是值得研究的主题［12］。

3 研究结论与展望

3.1 研究结论

从目标数量、“府际”关系和求解算法三个维度，本文对基于数学规划的救援物资分配优化模型及其求解算法进行了综述。结合表1～3的结果，分析相关发展趋势，结果表明：

1）从构建的救援物资分配优化模型的目标函数数量而言，相关研究从仅仅关注时间/成本/死亡人数等最优化的单目标规划模型向综合考虑社会、经济和环境的多目标规划模型延伸。

2）从救援物资分配活动中利益相关者间的“府际”关系而言，相关研究从仅考虑横向“府际”关系的救援物资分配优化问题向综合考虑横向与纵向“府际”关系的相关问题领域拓展。

3）相关研究从确定条件下的救援物资分配优化问题向不确定（如模糊）条件下的相关问题领域发展；从传统视角下的救援物资分配优化问题向融入救援过程可持续发展理念的相关问题领域发展；从静态环境下的救援物资分配优化问题向动态环境下的相关问题领域发展。

4）从设计的求解算法而言，随着救援物资分配问题规模不断增大，问题复杂程度不断增加，相关研究从精确算法设计向启发式算法设计拓展，从单一算法设计向融入多种策略的复合算法设计发展。此外，从面向单层规划模型的求解策略设计向面向双层（或多层）规划模型的求解算法设计发展。

5）相关研究聚焦于传统技术在救援物资分配问题中的应用，较少关注新信息与通信技术（Information and Communications Technology，ICT）背景下数据驱动的救援物资 分配模型构建的应用研究。

表3 救援物资分配数学规划模型求解算法文献总结Tab. 3 Summary of the literatures about algorithms to solve mathematical models of relief distribution

综上所述，基于数学规划的救援物资分配优化问题可从以下几个方面进行深入研究。

3.2 救援物资分配优化支撑框架构建

大多数文献聚焦于救援物资分配数学规划模型的构建、求解算法的设计等问题，但较少从根本上回答关键要素表达式建立、决策模型构建的内在机制。然而，曹策俊等［3］的研究显示，战略层面有效的机制分析对操作层面构建恰当且合理的数学规划模型至关重要，可为其提供科学的理论依据。因此，如何抽象、识别与提取应急响应决策系统的关键要素及其关联关系，如何有效刻画利益相关者间的横向与纵向“府际”关系，以及如何构建救援物资分配优化层次结构模型或支撑框架，这些都是未来值得研究的问题。

3.3 不确定环境下救援物资分配优化问题研究

已有研究成果更多地聚焦于探究确定条件下的救援物资分配优化模型构建和策略设计，然而，在大规模突发事件背景下，在黄金救援阶段，受影响区域的物资需求量、供应点的物资库存量，可利用的分配中心、应急需求点和供应点的数量都是不确定的［57］；并且，救援活动本身也具有不确定属性。另一方面，研究表明不确定性可采用模糊理论、鲁棒优化理论、随机优化等理论、区间数等来刻画。基于此，如何识别和量化救援物资分配活动的确定性特征，如何构建救援物资分配多目标模糊/鲁棒/随机规划模型、两阶段模糊/鲁棒/随机规划模型、双层模糊/鲁棒/随机规划模型，这些问题都是未来致力于解决的问题。

3.4 面向可持续发展的救援物资分配优化问题研究

研究表明，大多数学者聚焦于传统视角下的救援物资分配优化问题，较少关注融入可持续发展理念的相关问题。尽管有些文献已经涉及到可持续发展理念的某个或两个维度，但也并未明确强调与可持续发展的关系。自联合国颁布了包括《1994 年横滨战略行动计划》和《2015 年可持续发展目标》等在内的纲领性文件后，学术界开始呼吁将可持续发展理念融入应急管理决策问题中。例如，Cao 等［1］、曹策俊等［3］和Laguna-Salvadó 等［42］、Zarei 等［65］、Li 等［66］、Song 等［67］从不同方面强调了救援过程的可持续发展理念与救援物资分配优化问题结合的重要性。此外，充分理解和诠释救援过程的可持续发展理念，有助于促进该理念与救援物资分配优化问题的有机结合；运用OR/MS 方法定量刻画救援过程的可持续发展理念，是将可持续目标与救援物资分配优化模型无缝衔接的前提条件和理论依据。基于此，如何刻画突发事件情境下社会、环境和经济维度的可持续发展绩效，如何建立面向可持续发展的救援物资分配多目标规划模型、两阶段规划模型和双层规划模型，这些都是值得深入研究的问题。

3.5 求解救援物资分配双层规划模型的启发式算法设计

曹策俊等［57］、Lu 等［61］指出即使双层规划模型是线性的，其求解也非常困难。为提高求解效率，设计针对性的启发式算法是必要的和紧迫的。通过梳理文献发现，遗传算法和模拟植物生长算法分别作为经典和新的智能算法被广泛应用于求解数学规划模型。

具体地，现有研究主要针对救援物资分配单层规划模型设计遗传算法及其拓展算法，但较少关注如何设计支持“多准则决策建模、高不确定性和复杂性求解”的高效遗传算法。具体地，针对救援物资分配双层规划模型，如何设计带精英策略且下层采用分支定界法的嵌套式遗传算法，如何设计带精英策略且下层采用遗传算法的嵌套式遗传算法，如何提高遗传算法求解双层规划模型的效率，以及如何将遗传算法与其他算法融合形成新算法求解救援物资分配双层规划模型，这些问题都是需要进一步研究的方向。

针对模拟植物生长算法而言，它是学者李彤与王春峰于2005 年根据植物向光性动力机制和L-系统理论提出的全局类仿生算法［64］。该方法作为新的智能算法，凭借在时间和空间上的鲁棒性等优势，为求解各领域内的数学规划模型提供了新的思路和技术手段。在应急管理领域，模拟植物生长算法现阶段主要用于求解救援物资分配单层规划模型，如何设计支持“多准则决策建模、高不确定性和复杂性求解”的模拟植物生长算法亟待深入研究。基于此，未来的研究工作需要解决以下问题：针对救援物资分配双层规划模型，如何设计带精英策略且下层采用分支定界法的嵌套式模拟植物生长算法，如何设计带精英策略且下层采用模拟植物生长算法的嵌套式模拟植物生长算法，以及如何提高模拟植物生长算法求解双层规划模型的效率。

3.6 基于新ICT的救援物资分配数学规划模型构建研究

诸如云计算、大数据技术、数字孪生技术和区块链等新ICT 的兴起，对救援物资分配数学规划模型的构建或应急管理提出了新的挑战，但也带来了机遇［68］。随着时间的推移，新ICT 逐渐被广泛应用于各个领域。在应急管理领域，陈迎欣等［69］借鉴云计算和双目标优化思想，建立了基于任务-资源匹配的应急资源分配优化模型；Papadopoulos 等［70］利用非结构化和结构化大数据验证了可持续灾害供应链网络的韧性；Prasad 等［71］通过对12 个人道主义价值流案例的定性研究，建立了相应的资源依赖模型，将大数据分析与卓越的人道主义绩效联系起来。

尽管国内外学者运用ICT 对应急管理问题进行了有意义的探索，但其仍处于起步阶段；如何将大数据、数字孪生、区块链等新ICT 与救援物资分配问题深度融合还需深入研究。具体地，大数据可为救援物资分配策略的制定提供良好的数据环境和技术手段，提高应急决策的精度和可靠性，从而实现“经验驱动”向“数据驱动”决策模式转变的目标［72-74］。数字孪生作为践行智慧城市等先进理念的一种使能技术和方法，自2003 年在制造领域被提出后，得到了实践界和学术界的广泛关注［75-77］，为新时代救援物资分配优化建模提供了新的思路和方法。灾害发生属于无中心的事件，区块链作为去中心化的技术为应对灾害提供了有效的技术手段，可大幅度提高响应效率［78-79］。因此，以大数据为基础，如何探究事前、事中和事后调用救援物资的规则，如何构建数据驱动的救援物资分配决策模型，如何构建救援物资物理子系统、虚拟子系统、智能决策服务系统，以及如何建立相应的孪生数据库，如何理解和诠释区块链驱动的救援物资分配决策优化问题，以及如何构建基于区块链技术的救援物资分配数学规划模型，这些问题都是未来的研究方向。

4 结语

为了提高救援物资利用率，本文聚焦于数学规划方法在救援物资分配优化问题中的应用（模型构建及其求解算法设计）研究现状。从目标函数数量、“府际”关系两个维度，对救援物资分配数学规划模型的研究现状进行了综述；从精确算法和启发式算法两个方面，梳理了求解救援物资分配数学规划模型的算法的研究进展；从支撑框架、不确定环境、可持续发展、启发式算法和新ICT 五个方面，提出了救援物资分配优化问题的未来研究方向。总体而言，尽管学术界对基于数学规划的救援物资分配优化问题进行了大量研究，但在新时代背景下其仍然面临诸多挑战。在未来研究中，需将应急管理理论与实践更密切地结合，提高算法/软件的求解效率，关注新的ICT（如区块链、大数据）对救援物资分配带来的冲击，从而进一步完善和丰富理论研究成果。