基于噪声抵消与波束形成的小阵语音增强
2020-09-04曾庆宁
龙 超,曾庆宁,罗 瀛
(桂林电子科技大学电子工程与自动化学院,广西桂林541004)
0 引言
语音增强对于语音通信和语音识别具有重要的应用价值[1]。语音增强可分为单通道语音增强[2-3]和阵列语音增强[4-5],由于阵列语音增强含有多路信号,其增强效果通常优于单路语音增强。在阵列语音增强中,由于小阵的孔径很小,十分有利于嵌入诸如手机、电话、助听器等小型设备之中,应用场合更为广泛[6-7]。
广义旁瓣抵消(Generalized Sidelobe Cancellation,GSC)方法是阵列语音增强中的一种传统方法[8-11],但由于小阵中各通道的语音与噪声信号相互串扰的现象十分严重,GSC 方法的增强效果十分有限,于是基于VAD(Voice Activity Detector)的 GSC 方法被提出,即 VAD-GSC 方法[1,6]。而阵列抗串扰自适应噪声抵消(Array Crosstalk Resistant Adaptive Noise Cancellation,ACRANC)方法对于处理小阵中信号串扰的问题往往具有比VAD-GSC更加明显的优越性,因而ACRANC语音增强方法被提出[12]。对于小阵语音增强,ACRANC 方法通常比VAD-GSC 方法效果更为显著,尤其是当语音源和噪声源距离阵列较近时,其优势尤为突出。
本文旨在进一步改进ACRANC 小阵语音增强方法,通过将ACRANC 方法与波束形成(BeamForming,BF)方法[13]相结合,提出一种效果更好的小阵语音增强方法。基本思路如下:在ACRANC 中,取一路含噪语音信号作为主信号,其余路信号作为参考信号,其输出信号是主信号中经过降噪后的语音增强信号。由于主信号其实是可以任意选取的,如果分别把小阵中的每一路信号取作为主信号,其余信号作为参考信号,分别应用ACRANC 便可得到多路经过降噪后的语音增强信号。如果对这些多路语音增强信号进一步使用BF 方法进行降噪处理,将可得到更好的语音增强效果。为此,本文探讨并给出了ACRANC 与延迟求和(Delay And Sum,DAS)波束形成[13]相结合的方法。真实环境下的实验结果表明,本文方法可以进一步提高ACRANC方法的降噪效果。
1 阵列抗串扰自适应噪声抵消
假设语音信号为s(k),噪声信号为n(k),它们通过多条路径分别到达麦克风Mi并转化成信号si(k)和ni(k),语音和噪声从语音源和噪声源到达麦克风Mi的传播冲激响应为hsi(k)和hni(k),相应的Z变换分别记为Hsi(z)和Hni(z)。如图1 所示,麦克风Mi实际拾取的信号可表示为xi(k) = si(k) + ni(k),其中i = 1,2,…,N,k = 0,1,2,…,这里N 表示阵列中麦克风的个数,k是离散时间序号。
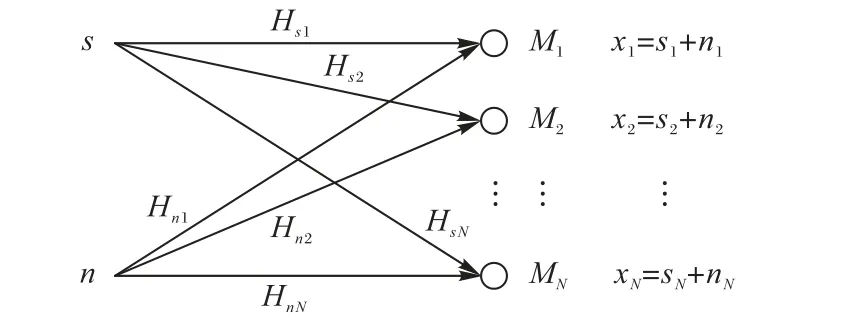
图1 语音与噪声的传播及串扰示意图Fig.1 Schematic diagram of propagation and crosstalk of speech and noise
由图1可得出:

其中:i = 1,2,…,N;*是卷积运算符号。
记语音信号si到语音信号sj的中间传播的冲击响应为hsjsi(k),而噪声信号ni到噪声信号nj的中间传播冲击响应为hnjni(k),则:

其中i,j = 1,2,…,N。由式(2)~(5)可得:

其中i,j = 1,2,…,N。
图2 所示即为一个ACRANC 系统结构,该系统以麦克风Mi获得的信号xi(k)作为主路信号,而其他N - 1 个麦克风获得的信号xj(k)(j = 1,…,i - 1,i + 1,…,N)作为参考信号。
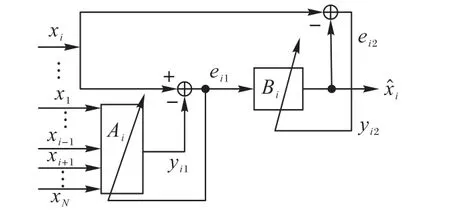
图2 ACRANC结构Fig.2 Structure diagram of ACRANC
首先,在全局无声阶段(即各路信号均属于无声的阶段),通过滤波器Ai用多路参考信号中的噪声去抵消主路中的噪声。
在全局无声阶段,可以假定语音信号si(k) = 0(i =1,2,…,N)。因此由图2有:

所以:

其中:xi(k) = ni(k),ei1(k) = erri(k)是预测误差,yi1= wini(k)是滤波器Ai的输出。wi是1×(N - 1)(L + 1)维的滤波器Ai的系数向量,即
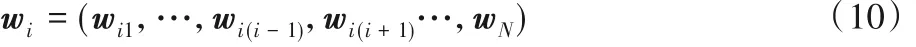
其中 wij=(wij0,wij1,…,wijL);ni(k)是N(L + 1) × 1 维的噪声信号向量。
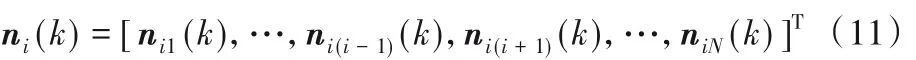
其中:nij(k) =[nij(k),nij(k - 1),…,nij(k - L)]T,显然L 是参考通道噪声信号延迟的样点数。
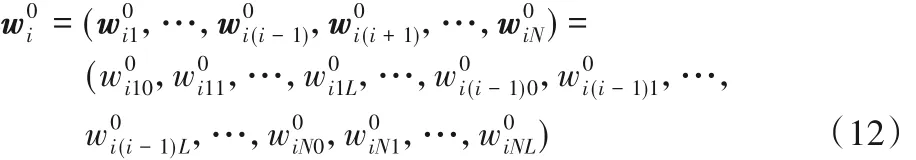
然后,在紧随全局无声阶段后面的有声阶段,在假定环境是不变或缓慢变化的条件下,不妨保持滤波器Ai的最优系数不变,于是有:
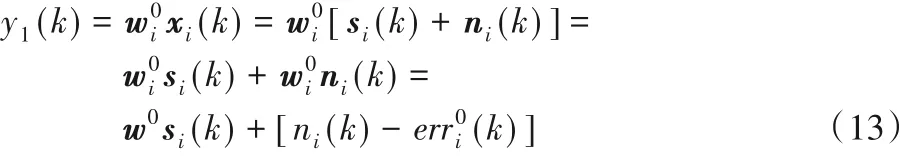
这里xi(k)和si(k)分别表示拾取的含噪语音向量和纯语音向量,表达形式类似于式(11)中的纯噪声向量ni(k)的形式。然后由式(8)与式(13)有:
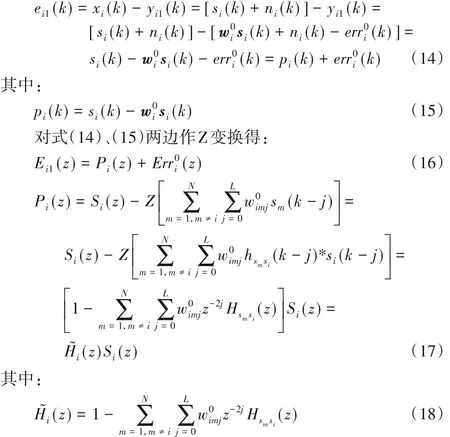
上述ei1(k)是一路含有残余噪声的畸变语音,pi(k)便是其中的畸变的语音,由式(15)可见,它其实由第i 路中的纯净语音信号si(k)畸变而来。
ei1(k)是将第i 路信号作为主信号,其他信号作为参考信号而得到的。如果让i 从1 至N,即分别将各路信号当作主信号,其余信号作为参考信号,那么就可得到N路含残余噪声的畸变语音信号ej1(k)(j = 1,2,…,N)。
如果滤波器Bi的系统函数为,则由式(17)和式(18)有:
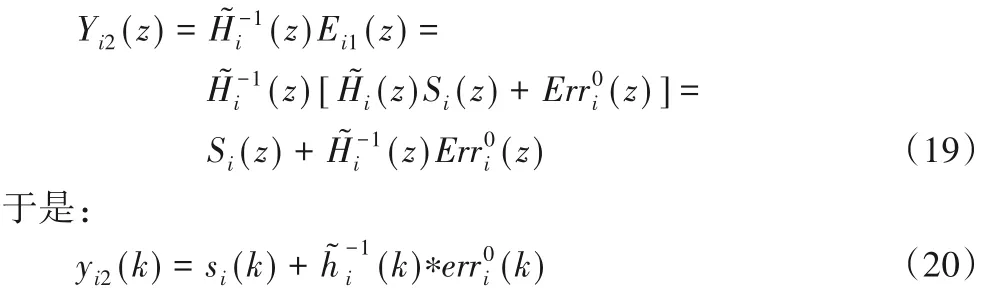
如同在自适应噪声抵消(Adaptive Noise Cancellation,ANC)系统中一样,不妨假设噪声与语音信号是不相关的,那么ni(k)与si(k)不相关,于是,为使滤波器Bi的系统函数趋于只需调节图2 中滤波器Bi的系数使的平方和最小即可,这是因为:
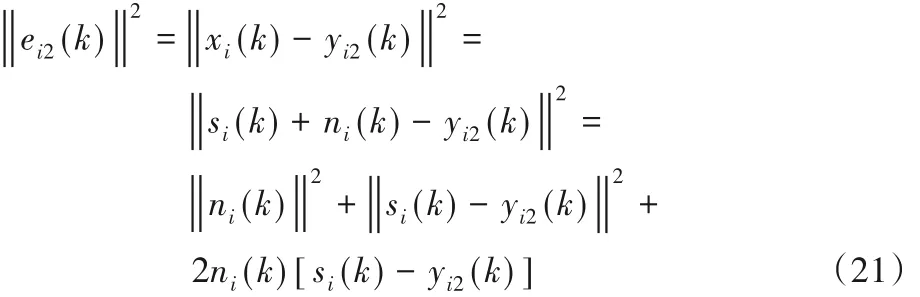
而:
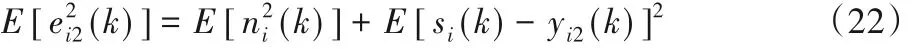
由上述分析可知:图2 的ACRANC 系统的输出yi2趋于纯净语音 si,记 x^i(k) = yi2(k)。
2 ACRANC结合波束形成方法
2.1 方法描述
第1章的ACRANC 方法可以与波束形成方法结合形成更为有效的语音增强方法,本文考虑与延迟求和(Delay And Sum,DAS)波束形成[15-16]相结合的方法。如图3 所示,该方法由N 个 ACRANC 子系统、1 个延迟求和波束形成(BF)子系统和1 个自适应模式控制(Adaptation Mode Control,AMC)子系统组成,其中N 为阵列中麦克风的个数。图3 中每个ACRANC 子系统均由虚线矩形框框出。AMC 用于控制这些子系统中的滤波器何时更新系数以及何时固定系数不变。每个ACRANC 子系统的输出也都是一路初步增强的语音,而所有子系统的输出再输入一个DAS 波束形成器以得到更好的语音增强结果。
2.2 关于AMC
在实际问题中,环境因素大多是缓变甚至基本不变的,因此,可以仅在没有语音的无声阶段(Non-Voice Period ,NVP)[14]调整滤波器Ai的最优系数以补偿环境因素变化引起的误差。由于语音到达麦克风阵中不同麦克风的时间不同,各个麦克风拾取得的信号的无声阶段也略有不同,因此这里需要定义一个全局无声阶段(Over-all NVP,ONVP),各个子系统的第一级滤波器Ai只在ONVP期间调整最优系数。
由麦克风Mi拾取得第i路含噪语音信号xi(k)的无声阶段记为NVP(i),NVP(i)显然由一系列离散区间组成,即:

定义ONVP为:

于是,容易证明:


图3 ACRANC结合波束形成方法示意图Fig.3 Schematic diagram of ACRANC combined with beamforming method
调整滤波器Ai的最优系数时,任何一路信号中最好都不含有语音信号,否则,语音会被当作噪声一同抵消,因此,只在如下的L-ONVP阶段调整滤波器Ai的系数。

其中L是参考信号输入滤波器Ai的延迟时间点数,而:
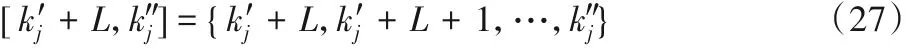
如果k″j< k′j+ L,同样定义式(26)中[k′j+ L,k″j]= ∅。
在L-ONVP 阶段,所有信号及本文用到的延迟全部属于无声阶段,不包括任何语音信号,因此可以在L-ONVP 阶段调整滤波器Ai的最优系数,第1 章中所指的特殊的NVP 阶段指的就是L-ONVP或L-ONVP的一部分。
现在已有许多语音判决方法可以用来判决一个含噪语音信号的 NVP 阶段或者 VP(Voice Period)阶段[13],但要准确地确定VP 或NVP 还是很难的,好在本文系统实际上并不需要准确地确定VP 或NVP,只要在NVP 内确定出一段纯噪声来更新所有滤波器Ai的最优系数以补偿噪声环境的变化即可,因此,其实可以使用一个比较简单的语音判决方法。进而,为计算简便起见,完全可以仅对某一路信号xi0(k)进行语音判决即可,不必要根据上述式(23)~(27)对全部N 路信号都作判决,为此,可以只在如下定义的(Δ,Δ′)-ONVP 阶段进行滤波器Ai最优系数的调整。
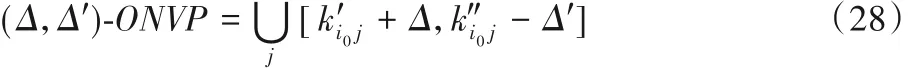

其中δ 是噪声从麦克风阵的其他麦克风传播到第i0个麦克风之间的时间延迟,以延迟样点数计。最多延迟样点数为:

其中:di是麦克风Mi0与麦克风Mi之间的距离;f 是阵列的采样频率;而c是音频信号在空气中的传播速度。
在(Δ,Δ′)-ONVP 之外的阶段,每个子系统的滤波器 Ai的最优系数保持原值不变,滤波器Ai只作滤波使用。
类似地,可以定义一个特殊的有声阶段的子集(Δ,Δ′)-OVP(Overall Voice Period),为了补偿环境变化以及说话位置移动而引起的语音传播函数的变化,应当在这个有声阶段的子集里自适应地调整所有滤波器Bi的最优系数。但实际应用中,如果为了简便起见,也可对Bi自始至终不停地作自适应滤波。
总而言之,通过阵列中某一路信号用VAD 定出无声阶段的子集(Δ,Δ′)-ONVP,在此子集内,所有子系统的滤波器Ai都作自适应滤波,而滤波器Bi始终作自适应滤波。
2.3 DAS波束形成
根据图3 所示的方法,每一个子系统的输出都是一路降噪后的语音信号,所有的N 路输出可以输入一个波束形成器以得到更好的语音降噪效果。本文使用常用的DAS 波束形成器,该波束形成器可通过如下的输入输出关系描述:

式中,τi是相对于阵列中选定的一个参考麦克风Mi0而言,语音到达麦克风Mi的延迟时间。参考麦克风Mi0可以任选为阵列中任何一个麦克风,但通常选择位于麦克风阵中央或接近中央的麦克风作为参考麦克风,显然τi0= 0。
如果麦克风阵的阵列孔径很小(小型阵列通常如此),而且阵列信号的采样频率不是很高的话,所有的τi可视为0 处理。例如,如果阵列中任何一个麦克风Mi到参考麦克风Mi0的距离都小于2 cm,而且阵列的快拍采样频率为8 000 Hz,那么最大的延长时间将小于半个采样时间间隔,所以,这时不妨取所有的τi= 0。
2.4 计算复杂度
对于图3 所示的语音增强方法,其中AMC 和DAS 波束形成器的计算量都不大,AMC其实可以通过一个VAD 实现。所以,方法的计算复杂度主要在于N 个子系统的ACRANC 方法的计算量估计,对于ACRANC,其计算量取决于所有滤波器Ai和Bi所采用的自适应算法。如果本文采用最小均方(Least Mean Square,LMS)自适应算法,则不难算出N 个子系统的ACRANC方法的计算量不超过:
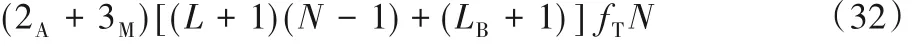
其中:2A表示2次加法运算;3M表示3次乘法运算;L是决定滤波器Ai阶数的式(10)中参考信号所用到的延迟时间样点数;N是阵列中麦克风的个数;LB是滤波器Bi的阶数;fT是麦克风阵列的采样率。由于许多芯片可以在一次操作中同时完成一个加法和乘法,其真实计算时间远少于式(32)所示所需要的时间。
例如,如果选取决定滤波器Ai长度的L = 24,滤波器Bi的长度LB= 48,采样频率fT=8 000 Hz,并且阵列由N = 5 个麦克风构成,则根据式(32)可得所关心的计算量将不超过29.8 MFLOPS,足见其可用目前普通的DSP芯片实时实现。
3 实验与结果分析
实验在普通室内进行,实验中所用的麦克风小阵如图4所示,由5个麦克风 M1,M2,…,M5置于一圆盘上组成,M1位于圆盘中心,其余四个麦克风围绕中心均匀放置,每个麦克风Mi(i = 2,3,4,5)与中心麦克风M1的距离仅2 cm。噪声由喇叭播出噪声库NoiseX92 中的多种噪声,喇叭与麦克风阵的中心距离为1.5 m。语音为一说话人朗读句子“本段语音用于测试”,说话人位于麦克风正前方30 cm 处。阵列快拍采样率为8 000 Hz。
实验数据一的录取是将语音和噪声分开发出并录取,然后再将它们叠加合成含噪语音阵列数据;实验数据二则是将语音和噪声同时发出并录取的含噪语音阵列数据。实验结果表明:本文方法对实验数据一与实验数据二的语音增强效果几乎没有差别,但使用实验数据二将无法进行信噪比(Signalto-Noise Ratio,SNR)计算和语音质量的 PESQ(Perceptual Evaluation of Speech Quality)评分[15-19],因此,以下不妨针对实验数据一给出实验结果。
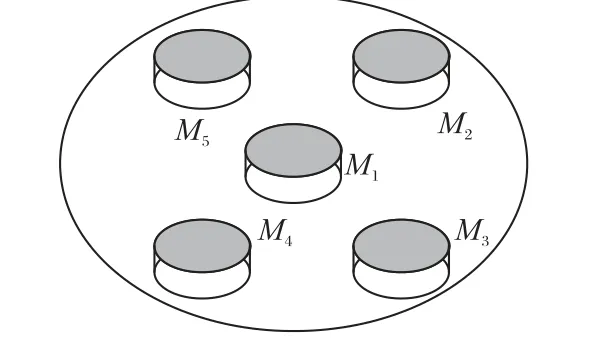
图4 麦克风小阵Fig.4 Small microphone array
在对实验数据进行语音增强的过程中,选取L = 24 和LB= 48,所以,每个ACRANC 子系统中,滤波器Ai的阶数均为(24 + 1) × 4 - 1= 99,滤波器Bi的阶数均为48。
采用最小均方(LMS)自适应算法来调节每个子系统中的有限脉冲响应(Finite Impulse Response,FIR)滤波器Ai和Bi的系数向量,而LMS 算法中步长因子选为μ = 0.01。同时,选择麦克风M1作为DAS 波束形成中的参照麦克风,并且,选择麦克风M1获得的信号x1(k)作为VAD 的探测信号。为获得(Δ,Δ′)-ONVP,选 Δ′= 100。由于阵列中麦克风距离很近,而且采样率不高,因此,语音在各麦克风中的延迟少于一个样点,于是为简便计算可将DAS 波束形成简化为求和波速形成。
表1 给出了针对多种噪声采用VAD-GSC 方法、ACRANC方法和本文方法的增强语音的信噪比SNR。从表1 中可以看出,ACRANC 方法的语音增强效果显著优于传统的VAD-GSC方法,而本文方法的效果相较ACRANC 方法又有所提高。表2 给出了针对多种噪声采用VAD-GSC 方法、ACRANC 方法和本文方法的增强语音的客观质量评分PESQ。从表2 中同样可以看出,本文方法具有更好的语音增强性能。
图5 是噪声为白噪声时各个有关信号的波形图。其中:(a)是麦克风M1拾取纯净语音信号;(b)是麦克风M1拾取的含噪语音信号x1(k),由其他麦克风拾取的含噪语音信号与x1(k)的图几乎相同;(c)是通过VAD-GSC 方法输出的增强语音信号,其SNR 改善了3.28 dB,PESQ 提高了0.05;(d)是对应图3 中第一个子系统的输出x^1(k),也就是使用ACRANC 方法增强后的语音信号,其SNR 改善了11.18 dB,PESQ 提高了0.23,其他四个子系统输出的语音信号的SNR 改善量分别为10.92 dB、12.09 dB、11.82 dB 和10.83 dB;(e)是通过本文方法输出的增强语音信号y(k),相较于中心麦克风拾取得含噪语音信号x1(k),其 SNR 改善量为 14.99 dB,而 PESQ 提高了0.41。
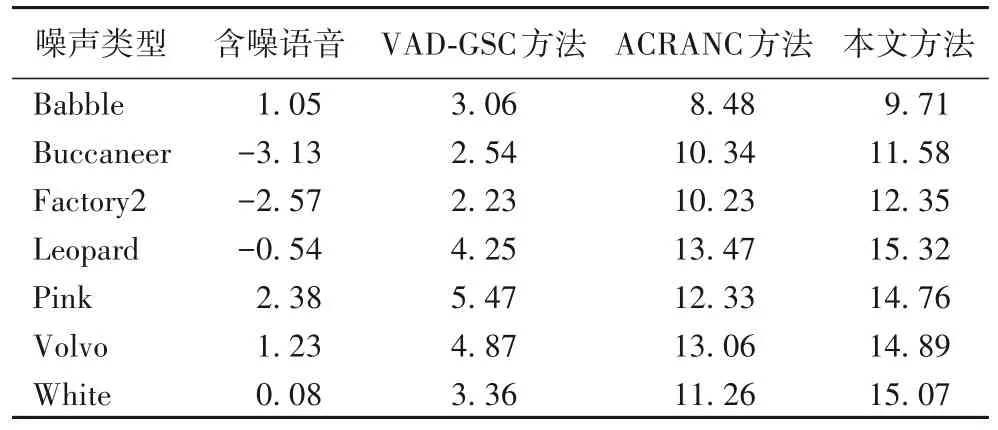
表1 针对多种噪声采用不同方法的增强语音信号的SNR单位:dBTab. 1 SNR of speech signals enhanced by different methods under several kinds of noises unit:dB
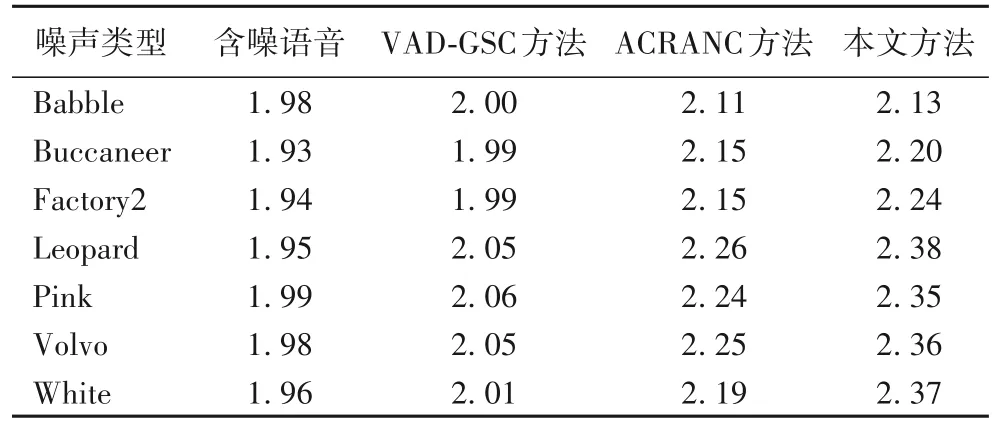
表2 针对多种噪声采用不同方法的增强语音信号的PESQTab. 2 PESQ of speech signals enhanced by different methods under several kinds of noises

图5 不同方法的语音增强信号波形图Fig.5 Waveforms of speech signals enhanced by different methods
4 结语
本文在阵列抗串扰自适应噪声抵消(ACRANC)方法的基础上,探讨并提出了ACRANC 与延迟求和(DAS)波束形成相结合的方法,分析了其语音增强原理及计算复杂度,真实环境下的实验结果表明了本文方法的有效性。
需要指出,经过本文方法处理后所输出的增强语音信号,还可以继续使用单路语音增强方法进行增强处理,以得到残留噪声更少的增强语音信号,但由于单路语音增强方法不可避免地会对语音信号造成损伤,因此,应根据具体应用情况决定是否再进行单路增强处理。
