基于非凸全变差正则的核磁共振图像重构算法

沈马锐，李金城，张 亚，邹 健

（长江大学信息与数学学院，湖北荆州434023）

0 引言

核磁共振成像（Magnetic Resonance Imaging，MRI）由于其有效的描绘软组织变化的能力，被广泛地运用于医学领域［1］。MRI 应用的主要限制因素是其成像的采集时间相对较长，为了加快扫描速度、减少数据采集量和采集时间而不降低重建质量始终是关注的焦点。稀疏重构模型能够从高度欠采样的信号中精确地重构图像，解决由于采集数据的限制和采集时间长的问题，因此在核磁共振成像中发挥着重要的作用［2-3］。

MRI 系统可以抽象为一个欠定线性方程组Ax = y，其中：x ∈RN为待重构的核磁共振图像；y ∈RM是磁共振线圈采集到的k空间信号；A ∈ RM×N（M ＜ N）为欠采样傅里叶变换。一般来说 A = P × F，P ∈ RM×N为欠采样模板，如径向采样模板、变密度随机采样模板、笛卡尔采样模板等；F ∈ RN×N为稀疏变换算子，如傅里叶变换、小波变换等。一般情况下，上述欠定线性方程组有无穷多解，但可以通过求解如下优化问题来唯一重构x，求解模型如下：

常用的稀疏正则包括L0正则、L1正则、Lp正则和全变差（Total Variation，TV）正则等。L0正则的一般形式为φ0(x) =，它表示稀疏解x 中非零元素的个数；但求解L0范数是个NP 难问题。L1正则是L0正则的凸松弛，目前使用最为广泛；但L1范数不可导且是一个有偏估计，对稀疏解中较大的值欠估计［5］。Lp正则虽然能更有效地估计稀疏解x 中的较大值，但由于目标函数本身是非凸的，求解过程往往非常困难，例如会陷入局部最优值。为了克服L1和Lp正则的缺点，Selesnick 等［6-9］提出了一类L1非凸正则构造方法，其基本思想是利用最小最大凹（Minmax-Concave，MC）罚函数，在 L1范数上减去其Moreau 包络。该正则项是非凸的，能有效估计稀疏解x中的较大值，同时该非凸正则能使目标函数整体保持凸性，可以利用已有的凸优化算法进行高效求解。该类非凸正则被广泛地应用于图像的去噪和重构上［10-11］。

TV 正则是另一种常见的稀疏正则，可有效地解决图像在噪声情况下的光滑问题［12］。它不仅能抑制图像的噪声，而且能保留图像的纹理、边缘等细节，因此被广泛地用于信号、图像的去噪或图像的重构［13-15］。TV 正则可分为各向异性和各向同性两种情况，通过引入差分矩阵，可以分别转化为L1范数和 L2范数［16］。目前对 TV 正则的研究主要以可转化为 L1正则的各向异性情况为主，如：文献［17］中基于Selesnick 的工作，利用基于L1范数的最小最大凹全变差正则（Minmax-Concave Total Variation of L1norm，MCTV-L1）来重构MR 脑图像。但正如文献［18］中所述，各向异性TV模型适用于那些呈现“块状”结构的图像，而对于自然图像，各向同性TV 模型要更加适合。因此，对可转化L2范数的各向同性TV模型的研究是很有必要的。

在稀疏重构问题中，高效的稀疏重构算法是保证稀疏重构得到广泛应用的关键，常用的稀疏重构算法大致可以分为贪婪算法、凸优化算法和神经网络算法三类［19-20］。交替方向乘子法（Alternating Direction Method of Multipilers，ADMM）是一种简单而有效的凸优化算法，其主要思想是通过分裂变量将无约束优化问题转化为约束问题，然后交替迭代求解。该算法被广泛应用于求解各种稀疏优化模型［21］，本文也考虑利用ADMM求解新提出的模型。

本文对核磁共振图像的重构模型和算法进行研究，提出了一种基于L2正则的非凸全变差正则重构模型。首先将Selesnick 构造非凸正则的思想应用到L2范数上，利用Moreau包络函数和MC 罚函数构造L2范数的非凸正则，提出基于L2范数的非凸TV 正则模型——（Minmax-Concave Total Variation of L2norm，MCTV-L2），并证明了该模型的目标函数在一定条件下是凸的；接着使用ADMM 优化算法来有效地求解新模型；最后利用仿真实验验证了所提模型的有效性。实验结果表明，该模型能更好地重构图像的纹理、边缘等细节，重构性能有显著提升。

1 L2范数的非凸正则

1.1 L2范数的Moreau包络和MC罚函数

Moreau 包络函数和MC 罚函数是构造L2范数的非凸正则常用的构造工具。其定义如下：

定义1 对于一个半连续函数f，定义其Moreau 包络函数为：

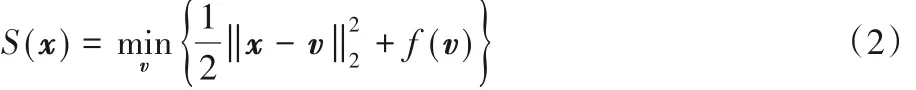
定义2 对于一个半连续函数f，定义其MC罚函数为：

对L2范数，其非凸正则构造过程［22］如下。

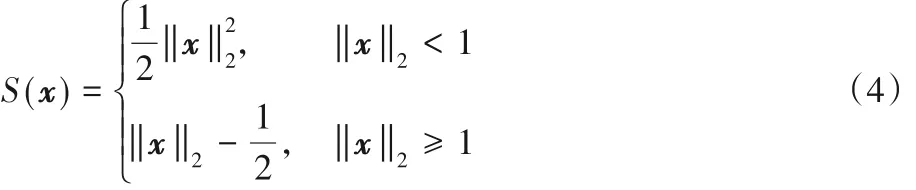
图1（a）为二维L2范数的图像，图1（b）为对L2范数进行平滑化处理后的Moreau 包络图像，平滑后的函数是原函数的可微紧下界，具有迭代形式的解析解，并且也是原函数的解［23］。

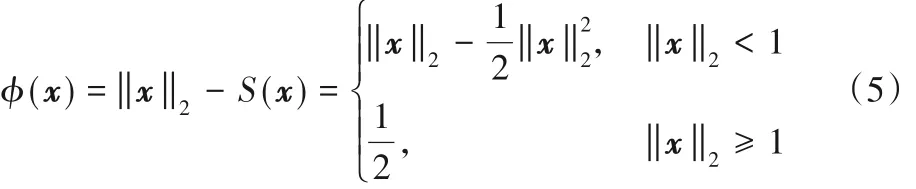
图1（c）为二维L2范数的MC 罚函数图像，从图像上可以看出MC罚函数是非凸的。

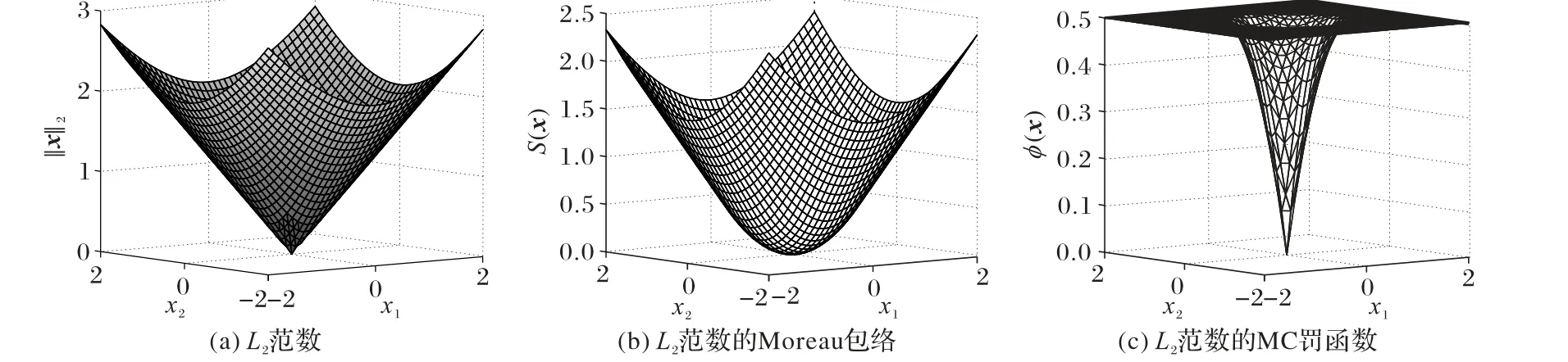
图1 L2范数及其Moreau包络和MC罚函数Fig. 1 L2 norm and its Moreau envelope and MC penalty function

1.2 L2范数的尺度Moreau包络和尺度MC罚函数

式（5）中MC 罚函数的非凸性是固定的，为了更好地控制其非凸性，可以引入一个参数b(b ＞0)来构造L2范数的尺度Moreau包络和尺度MC罚函数。

定义 5 令 b ＞ 0，对于函数 f(x) =‖x ‖2，定义其尺度Moreau包络函数为：

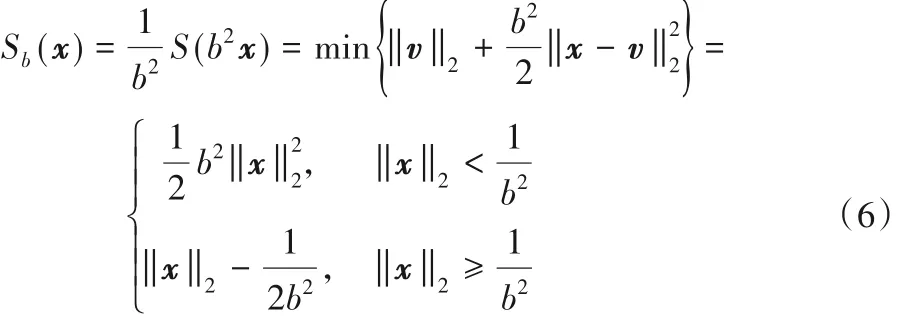
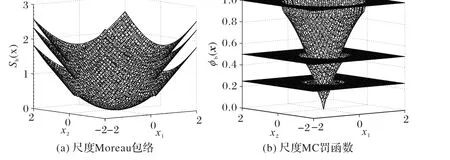
图2 L2范数的尺度Moreau包络和尺度MC罚函数Fig. 2 Scaled Moreau envelope and scaled MC penalty function of L2 norm

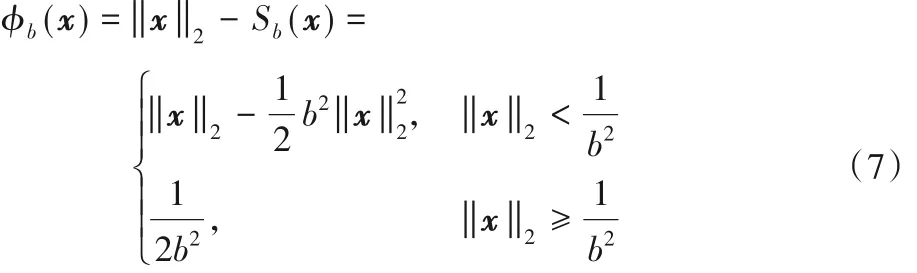
2 TV范数的非凸正则

L1正则化模型在图像重构过程中未能考虑图像中像素点与其邻近点水平和竖直方向上的关系，常导致图像边缘特征严重缺失和重构图像不够光滑、包含噪声等问题，TV 正则充分考虑到图像的结构特征，能有效抑制图像的噪声而且能保留图像的纹理、边缘等细节，克服阶梯效应，实现空间分段光滑，使得空间信息得到更加充分的利用，极大提升图像的重构质量。TV 正则有各向异性和各向同性两种情况，可以分别转化为L1范数和L2范数。

假设x ∈RN为一幅图像，各向异性的情况可以转化为L1范数，即：

各向同性的情况可以转化为L2范数，即：

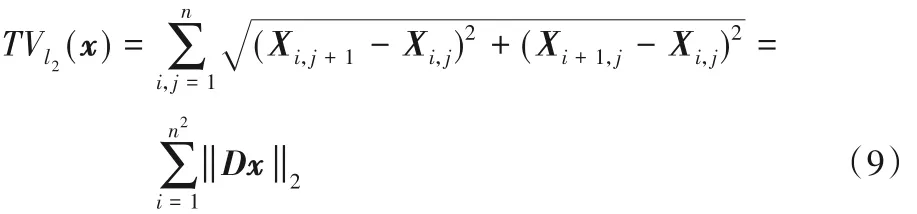
其中：X ∈ Rn×n表示与图像x相对应的矩阵；D ∈ R2×n2为有限差分算子；此外，通篇使用循环边界条件，记为

Selesnick 在文献［6］中提出了式（8）的非凸正则模型——MCTV-L1，文献［17］将该模型应用到MRI 重构上。本文将讨论式（9）的非凸正则模型——MCTV-L2。

定义7 令b ＞0，对于各向同性的TV 正则，定义其MC罚函数（MCTV-L2）为：

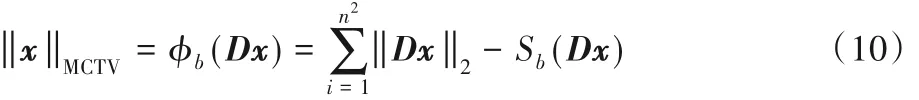
3 核磁共振稀疏重构模型

结合稀疏重构模型式（1）和MCTV-L2正则式（10），可得到基于非凸全变差正则的核磁共振图像重构模型如下：

定理1 令λ ＞ 0，b ＞ 0，x ∈ RN，定义Gb(x)为：

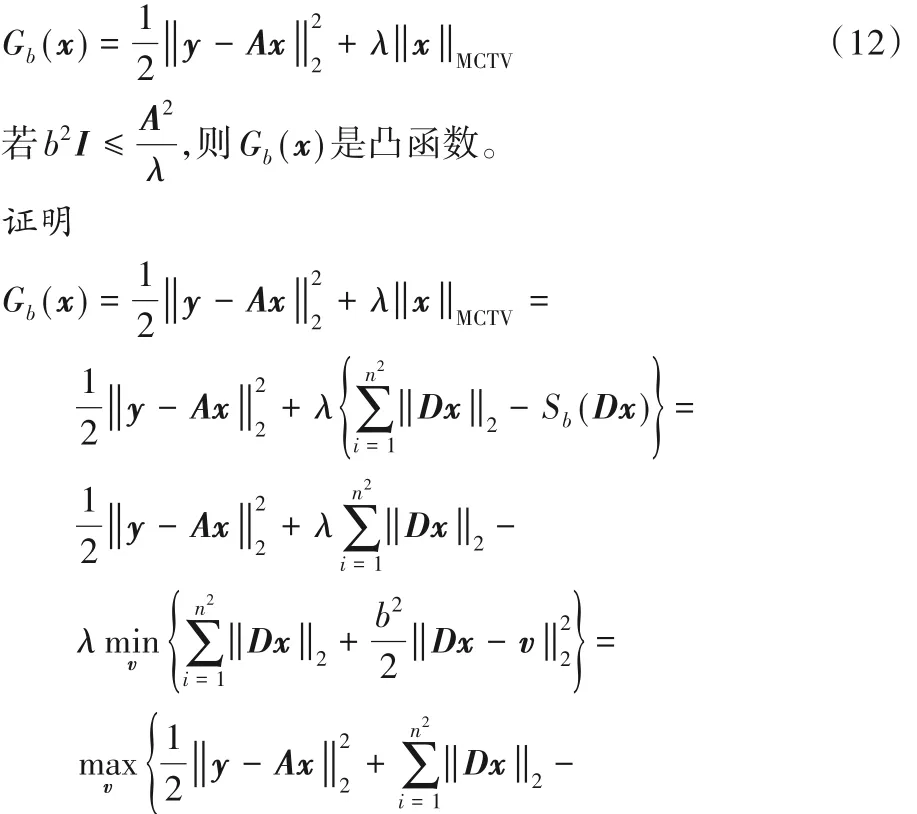
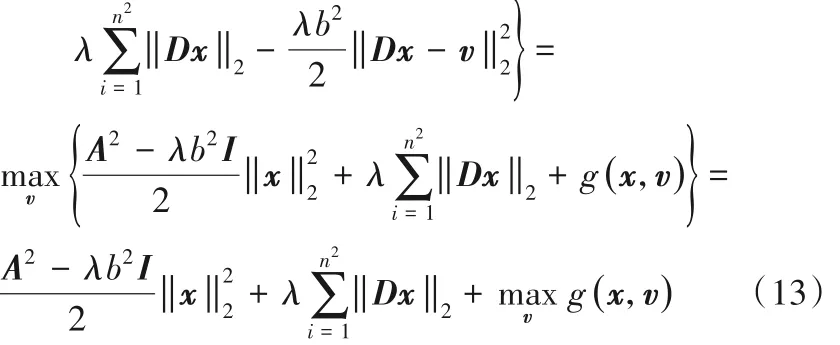
由于式（11）在一定条件下是一个凸优化问题，因此可以利用已有的凸优化算法进行求解，下一章将考虑利用ADMM算法来求解该问题。

4 ADMM算法

利用ADMM求解式（11）的主要步骤如下：

将式（10）代入式（11），可得：

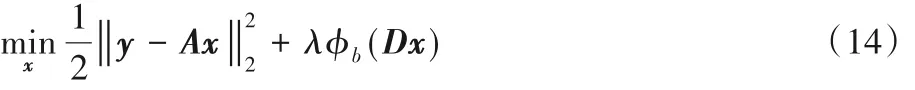
令z = Dx，可得到式（14）的增广拉格朗日形式如下：

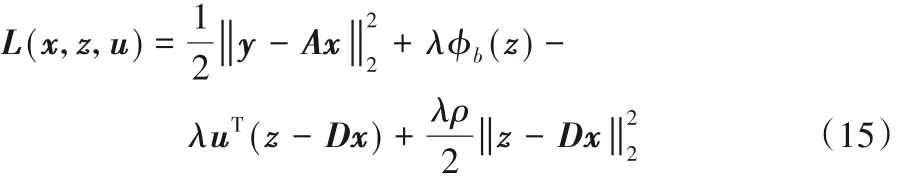
其中：u 是拉格朗日算子（对偶变量）；ρ 是惩罚参数项。ADMM 算法通过交替对 x、z、u 进行更新，找到式（11）的最优解。

步骤1 更新xk+1：

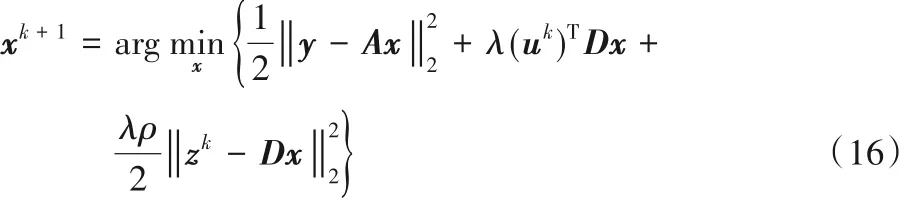
对式（16）求偏导，令其偏导等于零，可得：

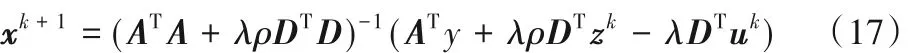
步骤2 更新zk+1：

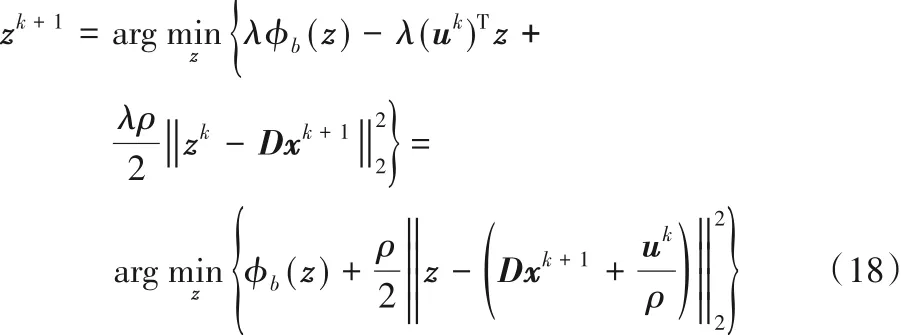
与参考文献［8，17］类似，式（18）可通过式（19）、（20）迭代步骤求解：

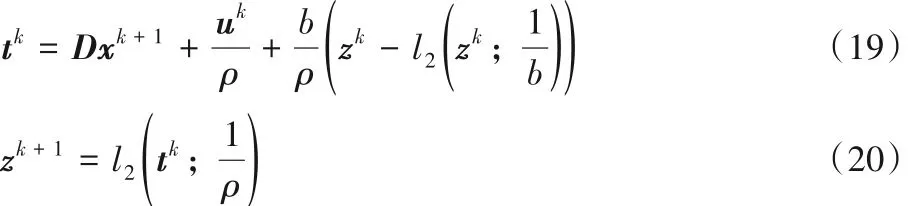
其中：

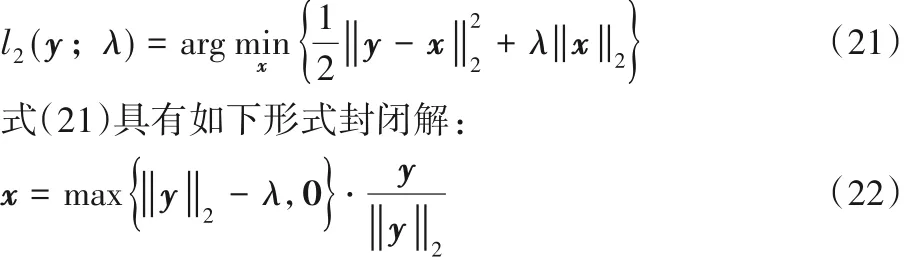
步骤3 更新uk+1：

综上可得求解模型式（11）的ADMM算法如算法1所示。

算法1 基于各向同性的非凸TV 正则化的图像重构算法。

输入：y

1） 初始化：x0= 0，z0= 0，u0= 0，λ ＞ 0，ρ ＞ 0，0 ＜ b ＜ ρ，

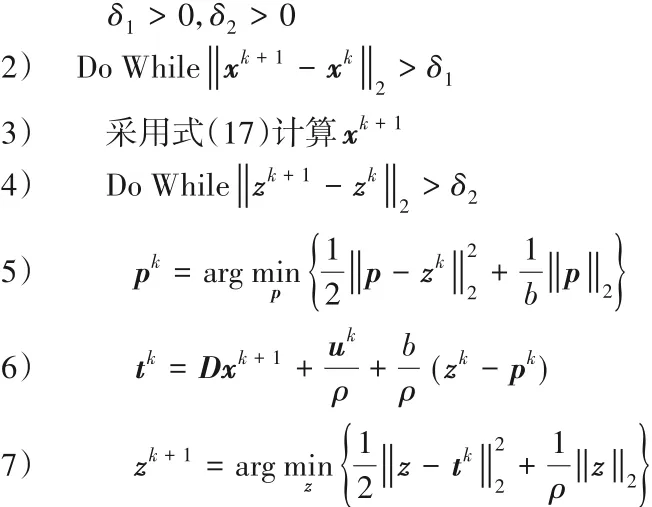
8） End Do

9） 采用式（23）计算uk+1

10） End Do

输出：x

5 仿真实验与结果分析

5.1 实验设置

为了验证本文MCTV-L2模型的有效性，将该模型与经典的各向异性TV 正则和各向同性TV 正则（分别记为TV-L1和TV-L2）以及文献［17］中的MCTV-L1模型对核磁共振图像重构的结果进行了对比。实验操作都是在Inter Core i5-4200M、2.50 GHz CPU、4.00 GB 的计算机上进行，编程环境使用Matlab 2018a。实验使用三种欠采样模板进行测试：径向采样模板、变密度随机采样模板以及笛卡尔采样模板，分别对Shepp Logan、大脑以及脑部血管共3 幅核磁共振图像进行重构结果对比，采样模板和实验图像如图3 所示。为方便比较，所有图像尺寸都设为256 × 256 像素大小，灰度取值范围为0～255，稀疏变换算子F 采用傅里叶变换。本文的实验代码和实验结果可以从网站链接https：//github. com/zj15001/MCTV_L2.git下载。

为保证比较的公平性，算法1 中参数的设置参考文献［17］中提到的最好的参数设置条件，即λ= 0.01，b= 0.05/λ，δ1= δ2= 0.000 1，ρ = 150。

5.2 实验评估标准

本文采用相对误差（Relative Error）和峰值信噪比（Peak Signal-to-Noise Ratio，PSNR）来评估图像重构的质量与准确性。相对误差VRE和峰值信噪比VPSNR的计算公式为：

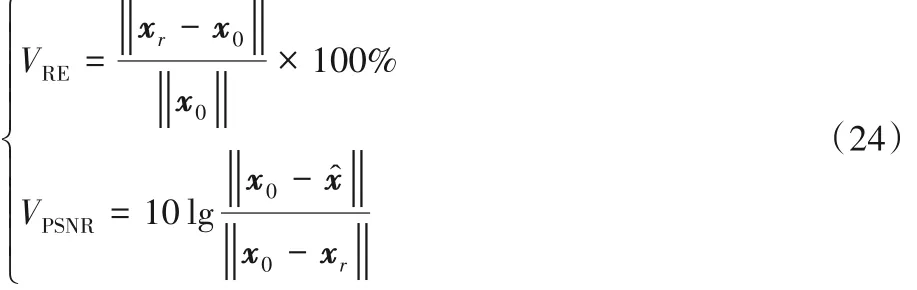
其中：x0为观测图像；xr为重构图像；x^ 为x0的均值。在这两种定量评估标准中，相对误差的值越小模型重构效果越好；而对于峰值信噪比来说，则是值越大，重构效果越好。在视觉效果评估中，对于每幅核磁共振观测图像分别给出了不同模型的重构效果以及重构图像与观测图像的差值图像，以便于更好地进行结果比较分析。

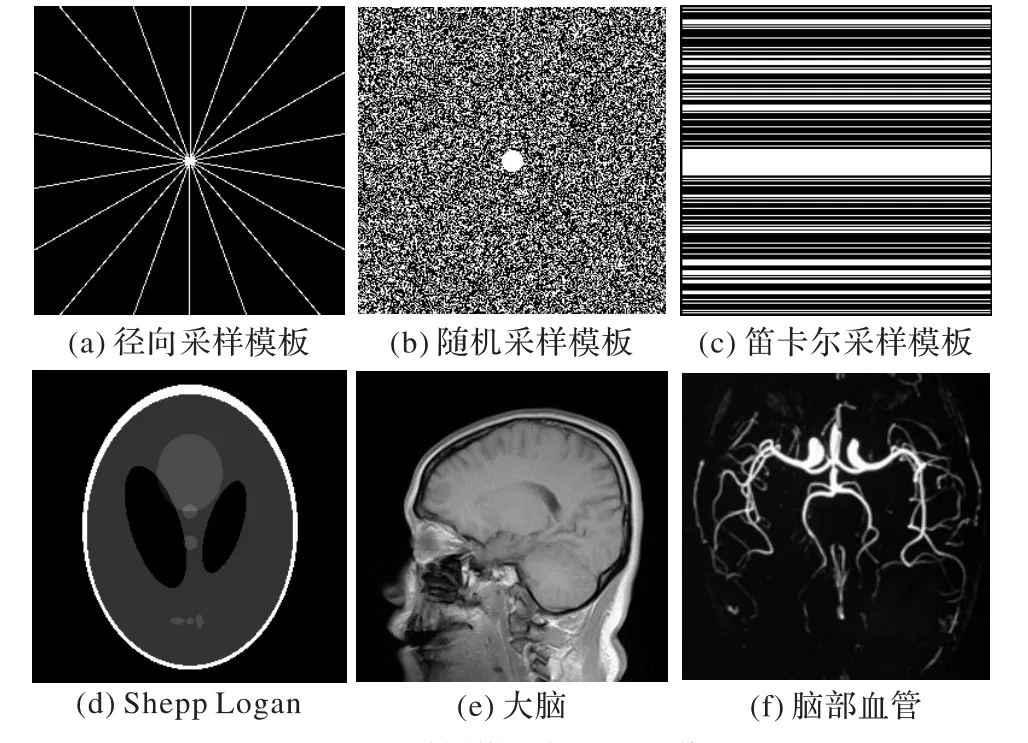
图3 采样模板与测试图像Fig.3 Sampling templates and test images

5.3 结果分析

本文实验分为两个部分，第一部分展示了算法针对不同的核磁共振图像和三种采样模板下的重构效果，视觉效果如图4～6所示，数值比较结果如表1所示。

首先，采用10 条线的径向采样模板，选择Shepp Logan 原始图像来对所提出的MCTV-L2重构模型进行测量，四种模型的重构效果与差值图像如图4所示。可以看到，使用TV-L1重构后的图像边缘比较模糊且伴有重影，而MCTV-L2模型重构后的图像更接近原始图像，在处理图像边缘信息时效果明显最好。如表1所示，使用TV-L1重构和MCTV-L2重构后的相对误差分别为0.36 和0.25，峰值信噪比分别为20.8841 dB 和24.0202 dB，显然MCTV-L2模型重构的实验数据最优。

为了验证MCTV-L2模型在变密度随机采样模板下重构图像的质量，选择采样率为30%的随机采样模板对像素大小为256 × 256 的大脑图像进行测试。如图5 所示：本文提出MCTV-L2模型在重构视觉效果上比前几种模型都好，重构后的大脑图像在视觉效果上与原始观测图像最相近，具体体现在大脑图像中边缘细节的重建以及对差值图像的对比。而TV-L1模型重构效果最差，不仅没有很好地重构图像，而且还丢失图像的很多边缘信息，看起来很模糊。

使用笛卡尔采样模板对脑部血管图像进行测量，沿相位编码方向仅用100条线对k空间数据进行欠采样，同时保持对频率编码方向的完全采样。四种模型重构后的图像效果与差值图像如图6 所示。显然，和其他测量图像一样，从视觉效果上看，新模型MCTV-L2重构后的图像效果优于其他三种重构方法。实验结果显示，MCTV-L2重构后的图像误差明显降低，峰值信噪比提升了大约4 dB。

由表1 可知，无论使用径向采样模板、随机采样模板还是笛卡尔采样模板，所有实验结果均表明，相较于TV-L1重构模型、MCTV-L1重构模型以及TV-L2重构模型，在核磁共振图像重构评估参数方面，MCTV-L2重构模型效果都是最好的，能得到更低的相对误差和更高的峰值信噪比，更好地重建平滑区域。

实验第二部分展示了采样率对核磁共振图像重构结果的影响。在变密度随机采样模板下，通过改变采样率，得到四种模型重构的图像与原始大脑图像的相对误差值的对比结果，如图7所示。

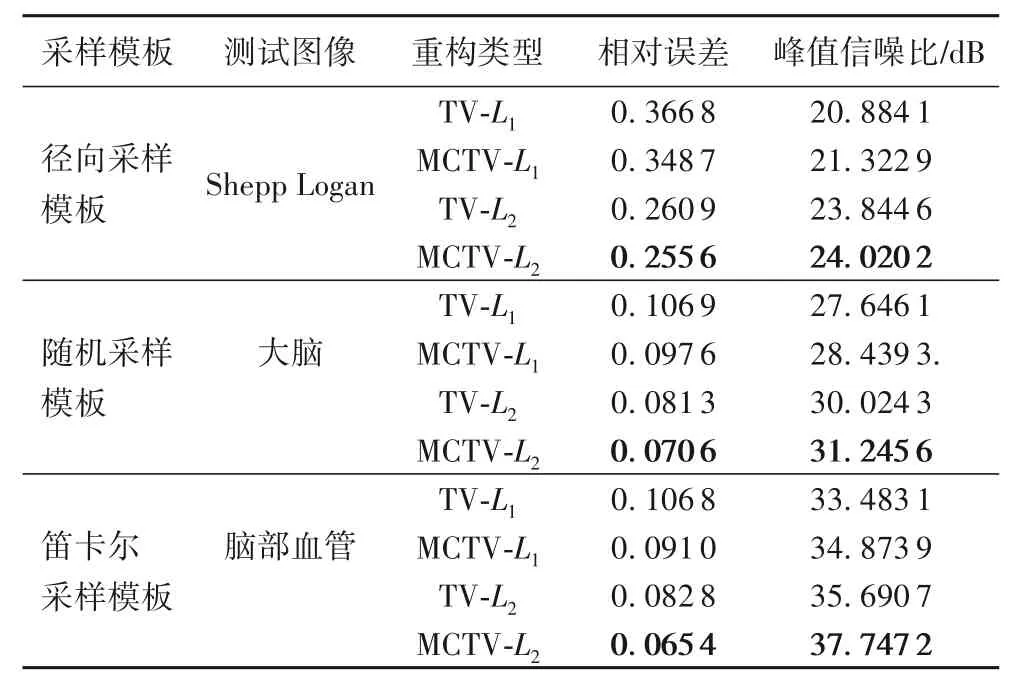
表1 不同采样模板下四种模型重构结果Tab. 1 Reconstruction results of four models under different sampling templates

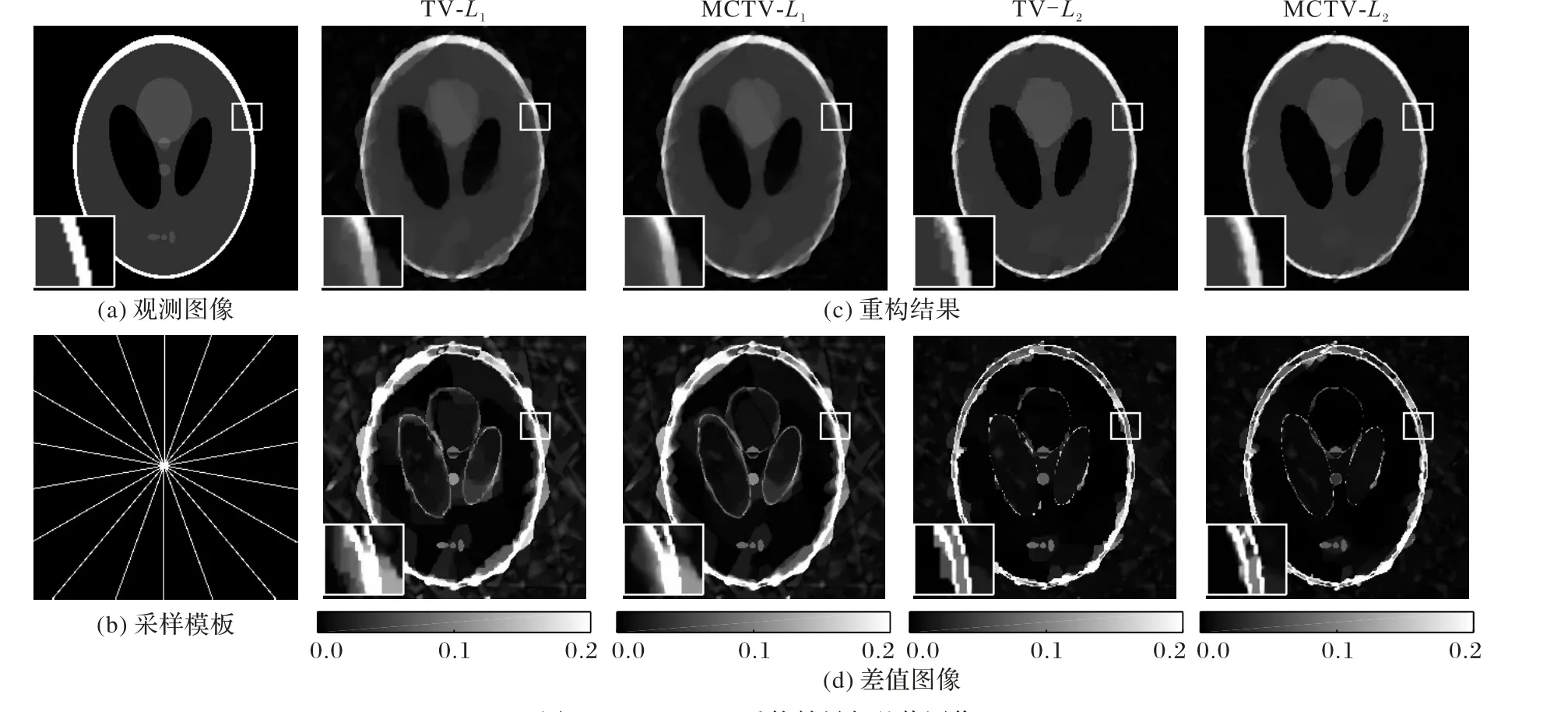
图4 Shepp Logan重构结果与差值图像Fig. 4 Reconstruction results and difference images of Shepp Logan

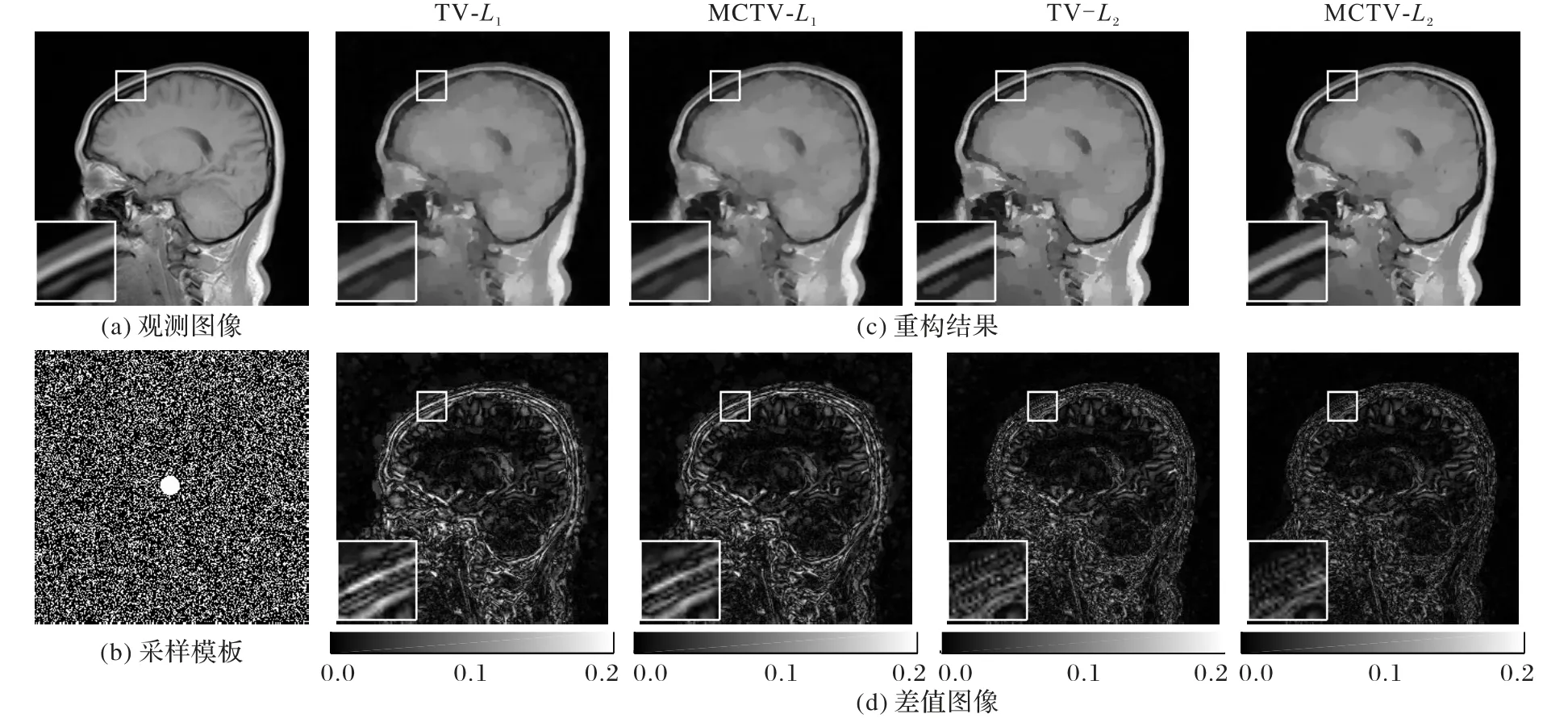
图5 核磁共振大脑重构结果与差值图像Fig. 5 Reconstruction results and difference images of MR brain

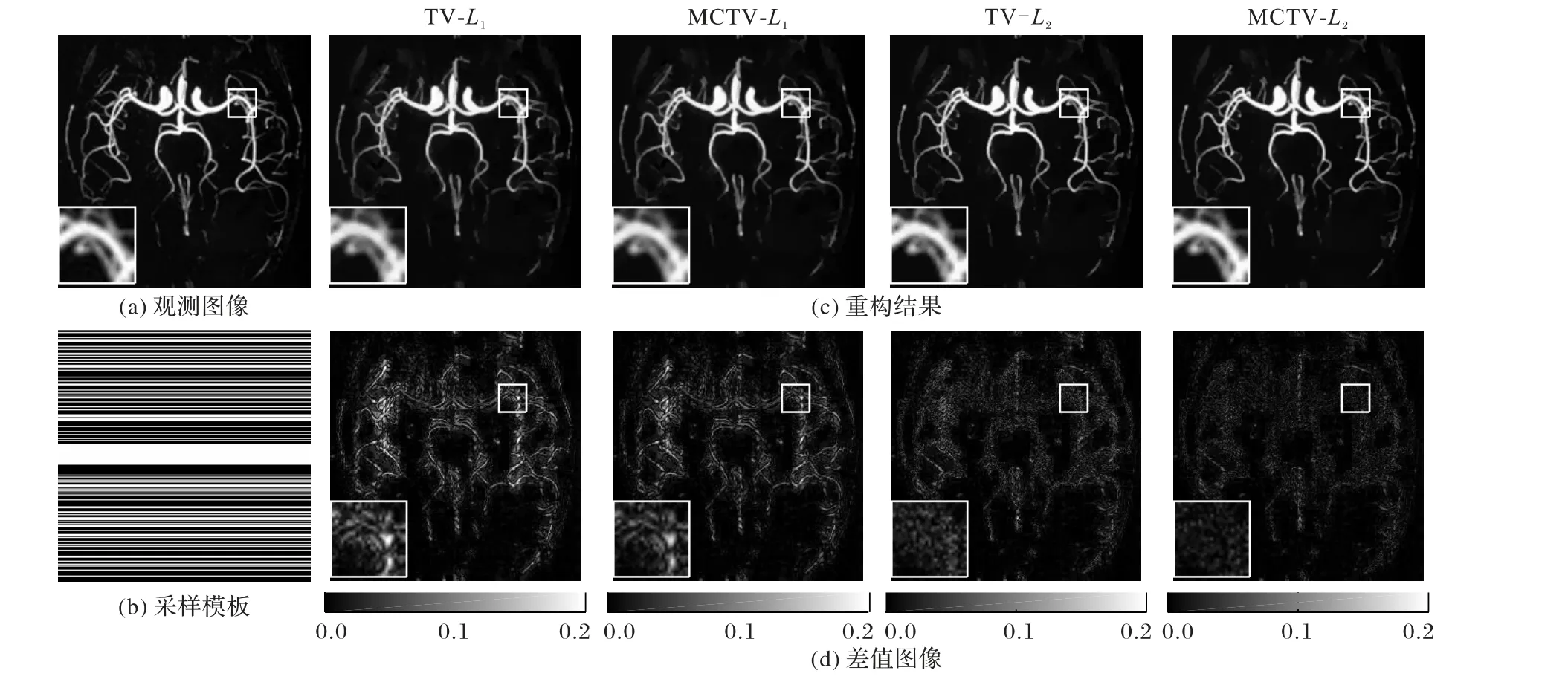
图6 脑部血管重构结果与差值图像Fig. 6 Reconstruction results and difference images of brain vessels

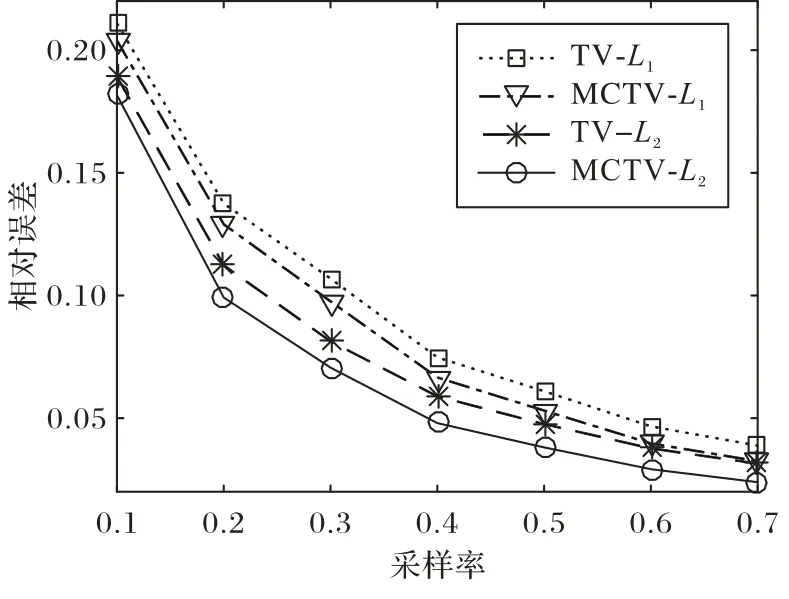
图7 大脑图像在四种重构模型下的相对误差与采样率的比较Fig. 7 Comparison of relative error and sampling rates of brain image under four reconstruction models

在不同采样率下，MCTV-L2模型重构后的图像与原始图像的相对误差值均低于另外几种模型重构后的图像与原始图像的相对误差值，且采样率越高，MCTV-L2重构后的图像与原始图像的相对误差值越低，在视觉效果上与原始图像更接近。实验结果表明，MCTV-L2模型具有非常不错的重构效果，与理论推断相一致。

6 结语

本文针对核磁共振图像重构中由于欠采样导致重构图像不够完整、边缘模糊以及噪声残留等问题，以Moreau 包络和最小最大凹罚函数为工具提出了一种基于L2正则的非凸全变差正则重构模型。相较于已有的重构模型，所提模型不仅可以有效地避免凸正则中对较大非零元欠估计现象，能够更有效地处理图像的纹理、边缘等细节，同时在一定条件下可以保证目标函数的整体凸性。在仿真实验中，利用高效的ADMM 算法对实验模型进行求解，将其运用于核磁共振图像的重构中。实验结果表明，相较于其他几种经典模型，所提模型MCTV-L2在重构效果上有明显的提升，能获得更高的峰值信噪比，视觉效果改善显著，能有效地消除图像伪影并在保留图像边缘轮廓信息基础上使图像更加光滑，具有非常不错的效果。由于基于各向同性的非凸全变差正则对于自然图像的处理效果要优于各向异性的方法，在进一步研究中，我们会考虑将该模型应用到其他图像处理领域。