面向类不平衡流量数据的分类模型

刘 丹 ，姚立霜 ，王云锋 ，裴作飞

（1. 重庆邮电大学通信与信息工程学院，重庆400065； 2. 移动通信技术重庆市重点实验室（重庆邮电大学），重庆400065）

0 引言

近年来，随着网民规模和互联网普及率的增长，网络流量分类在网络管理和网络安全等领域的重要性不断凸显［1］。传统基于端口号的流量分类技术［2-3］存在很大的局限性，在动态端口、伪装端口等技术出现之后，分类准确率很低。基于特征字段的流量分类技术通过分析数据包的有效载荷来达到分类的目的，虽然摆脱了对端口号的依赖，但却没办法处理加密流量，同时有可能会侵犯个人隐私［4］。基于传输层主机行为的流量分类技术，不依赖于端口号和报文载荷，但传输层主机行为对网络环境异常敏感，分类效果不够稳定。因此，研究人员逐渐把网络流量分类的研究重点放在基于机器学习的方法上［5-6］。

2005 年，Moore 等［7］首次将朴素贝叶斯（Naive Bayes，NB）用于网络流量分类，并系统地描述了网络流量的特征，为后来的研究提供了重要的依据；而且利用该数据集也证实了将贝叶斯神经网络用于流量分类的有效性［8］。徐鹏等［9］引入C4.5决策树方法来处理流量分类问题，避免了NB方法过分依赖于样本空间分布的问题，在分类稳定性上具有明显的优势。Chung 等［10］定义了一种两阶段的流量分类算法，利用基于余弦的流相似度函数进行分类，可以在非对称路由环境下取得较高的分类精度。杨哲等［11］采用基于最短划分距离的方法构建决策树分类，能够在分类准确性和系统开销上取得较好的效果。张震等［12］提出了“用户相似度”的概念，通过定义基于信息熵的“用户行为模式”，对用户行为子簇进行了业务标签映射，实现了流量分类的目的。丁要军等［13］提出一种基于互信息理论的选择聚类集成方法，以提高流量分类的精度。Punitha 等［14］提出一种基于增量学习的两级混合分类模型用于用户数据报协议（User Datagram Protocol，UDP）流量的分类，与现有的传统学习方法相比，该方法能提高混合分类器的分类精度。

文献［7-14］中方法的分类精确率都能达到较高的值，但是它们的分类性能大多在多数类（大类）上表现良好，忽视了分类器在少数类（小类）的预测精度，这就是类不平衡所带来的问题［15］。在网络流量分类领域，类不平衡问题可以表述为流量数据在各应用类别上的样本数量存在数量级的差距，导致分类器被多数类淹没，忽略了少数类。然而，人们在生活中通常更为关注小类的分类效果，错误识别小类别的代价往往很大，如入侵检测［16］。Shi 等［17］将深度学习与特征选择结合，提出了一种特征优化算法，能有效应对类别不平衡问题。同时，传统分类方法存在难以实现频繁、及时更新的问题，一旦要求更新，需要重新训练所有的数据，增加了时间和资源开销。

针对上述问题，本文提出一种基于集成学习的网络流量分类模型（Internet Traffic Classification Model based on Ensemble Learning，ELTCM），借助特征选择、增量学习、早期漂移检测以及集成学习方式提升模型的泛化能力以及在小类别上的分类性能。为验证本文模型的有效性，利用Moore 公开数据集［7］进行仿真，实验结果表明该模型能够在整体精确率、小类召回率、小类准确率和F1 值四个指标上均表现出较好的效果。

1 基于机器学习的网络流量分类方法

基于机器学习的网络流量分类技术利用网络流量在传输过程中表现出的统计特征（如数据包的数量、流的持续时间和数据包到达时间）区分网络类型［18］。

如图1 所示，一般基于机器学习的网络流量分类系统包含三个步骤：数据生成、学习过程和分类过程。数据生成阶段通过确定性策略以流形式对应用程序包进行手工标记，在计算、整合数据流信息之后得到流量统计特征，所得特征一般是多维的；学习阶段采用特征选择方法减少特征的维数，从整个特征集中选择最佳子集进行机器学习，通过一系列测试和评估选择合适的算法，训练生成分类器；分类过程则利用训练好的分类器分类未知流量。

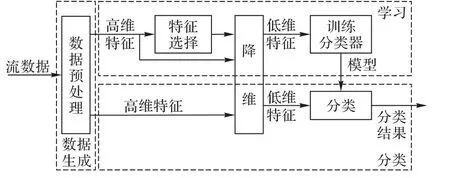
图1 基于机器学习的网络流量分类系统结构Fig. 1 Structure of Internet traffic classification system based on machine learning

在实际的网络流量分类中，将所有的流量特征都放入模型中进行训练是不明智的。一方面，某些特征可能和特定的应用程序无关，或者特征之间存在冗余关系，选择所有的特征进行模型的构建，可能会降低分类模型的准确性；另一方面，模型构建过程中选择过多的特征进行训练，会导致系统效率的巨大消耗，如需要从M个特征中选出m个特征组成特征子集，则存在种可能，当M的值很大时，存在的特征子集数目就很大，若单纯地使用穷举法，会浪费大量的时间和资源。为了对特征集合进行降维，获得最佳的系统性能，特征选择至关重要。

特征选择的流程如图2 所示，它主要包含生成特征子集（搜索策略）、评价准则、停止准则和结果验证［19］四个基本步骤。特征选择方法在原始特征集合中利用特定的搜索策略得到备选子集，并根据某种评价指标对选出的备选子集进行评价，由最优评估值的特征集合取代次优特征集合，并根据停止准则结束搜索，保证算法的有穷性，最后使用人工数据集或真实数据集测试所选子集的有效性。

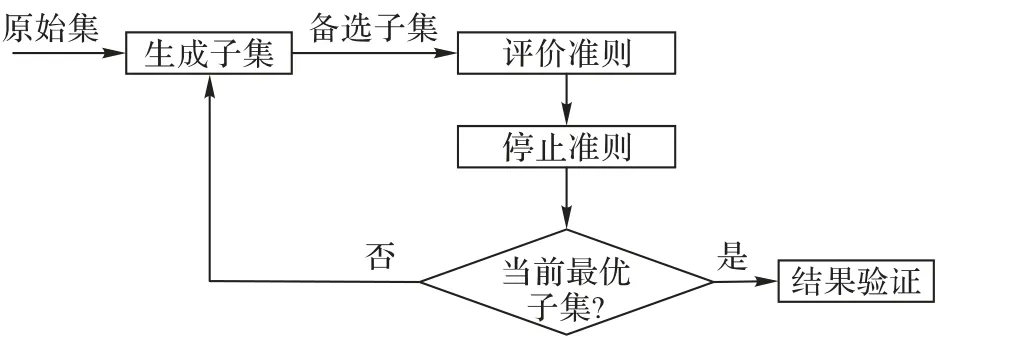
图2 特征选择流程Fig. 2 Flowchart of feature selection

2 基于集成学习的网络流量分类模型

基于集成学习的网络流量分类模型（ELTCM）系统结构如图3 所示。初始时，在预先获取的数据集上进行训练，得到一个基分类器；通过增量学习的方式，将新增的网络流量及其通过基分类器所得的分类结果作为新的数据子集；若新的数据子集与前一阶段的数据集相比，发生了概念漂移并达到一定程度时，采用新的数据集训练得到新的基分类器，并将新增基分类器加入集成分类系统，参与预测下一阶段的网络流量的分类结果。这样，当模型需要更新时，只需要利用少量的新样本进行训练，提高了模型更新训练的灵活性，缩短了模型更新的时间间隔。在训练基分类器时，提出一种基于加权对称不确定性（Weighted Symmetric Uncertainty，WSU）和近似马尔可夫毯（Approximate Markov Blanket，AMB）的特征选择算法，充分考虑特征与类别间、特征与特征之间的相关性，在删除不相关特征和冗余特征的同时，选出易于识别小类别的特征，减少类不平衡问题带来的影响。

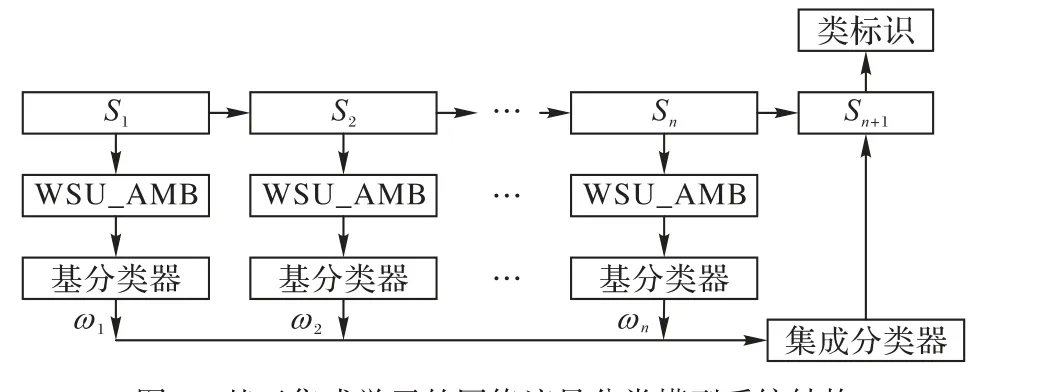
图3 基于集成学习的网络流量分类模型系统结构Fig. 3 Structure of Internet traffic classification model based on ensemble learning

2.1 WSU_AMB特征选择算法

WSU_AMB算法的总体结构如图4所示，它主要包含两个步骤：确定候选特征集合和获取最优特征子集。在第一步中，根据类别分布信息定义偏向于小类别的特征度量，使得识别小类别的特征更容易被选择出来，通过计算特征与类别间的加权对称不确定性，利用特征排序算法删除不相关特征，充分考虑特征与类别间、特征与特征之间的相关性，利用AMB 删除冗余特征，确定候选特征子集。在第二步中，采用基于相关性度量的特征评估准则函数和序列搜索算法进一步降低特征维数，获取最优特征子集。

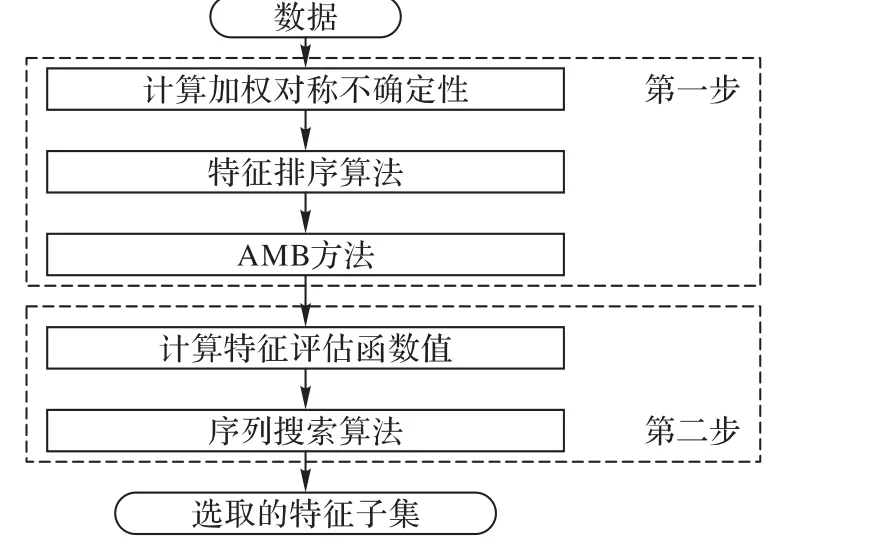
图4 WSU_AMB算法的总体结构Fig. 4 Structure of WSU_AMB algorithm

2.1.1 加权对称不确定性（WSU）

加权对称不确定性可以用来衡量特征与类别以及特征与特征之间的相关性，它是在加权信息熵的基础上计算出来的［20］，可以表示为：

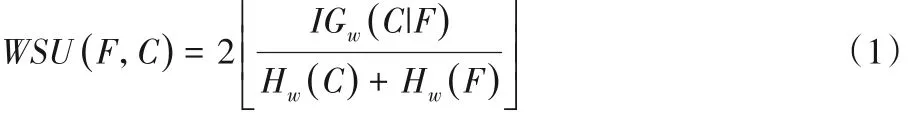
其中：

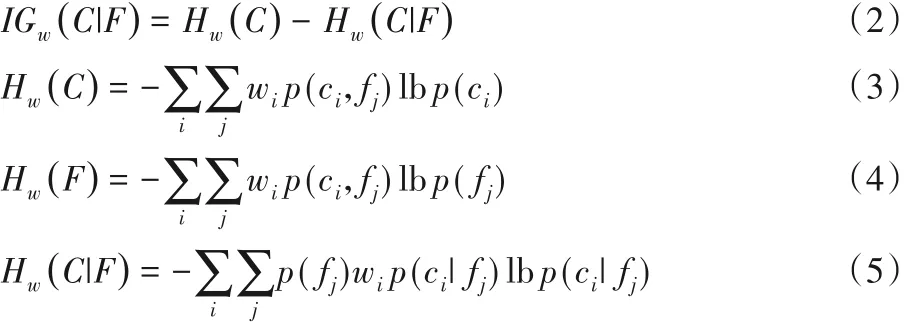
其中：p(ci，fj)表示类别 C 与特征 F 的联合概率；p(ci)表示类别C 的先验概率；p( fj)表示是特征 F 的先验概率；p(ci| fj)是 F 发生的条件下C的后验概率。

权值wi可以表示一个事件的重要性，根据类别分布信息，可以把权值定义为：

其中：ni表示属于类别ci的样本数；N表示样本总量。2.1.2 近似马尔可夫毯（AMB）

假设属性类别为C，特征集合为F，对于给定的特征fi⊂ F和特征子集M ⊂ F( fi∉ M)，若有：

则称能满足上述条件的特征子集M 为fi的马尔可夫毯。形象一点表述就是存在随机变量X、集合A 和B，且有X ∪A ∪B =U，X ∩ A ∩ B = ∅，U 为全集，如果在给定集合A 的情况下，变量X与集合B没有任何关系，则称集合A为变量X的马尔可夫毯。在式（5）中，集合M 即为所说的集合A，集合{F - M -{ fi}，C}即为所说的集合B。

在特征集合F 中，由于在特征fi的马尔可夫毯M 条件下，fi与其他非马尔可夫毯变量独立，因此，对于特征fi而言，所有非马尔可夫毯变量都是冗余的。但是马尔可夫毯的条件过于严格，现实数据难以达到要求，需要对该条件进行近似假设。

特征fi是特征fj的AMB(i ≠j)，需要满足以下条件：

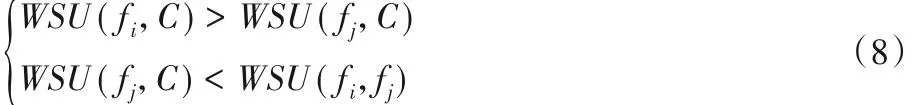
特征与类别之间的WSU 可由式（5）得到，特征与特征之间的WSU 的计算方法略有差别，此时需要将其中一个特征看成类别属性。在一个特征空间中，目标特征的所有信息均包含在它的AMB 中，非AMB 就可以看作目标特征的冗余特征，通过删除这些目标特征的冗余特征，就可以降低特征空间的维数。

2.1.3 相关性特征度量

在充分考虑特征的相关性的前提下，有效减少特征维数，提出一种特征准则评估函数：

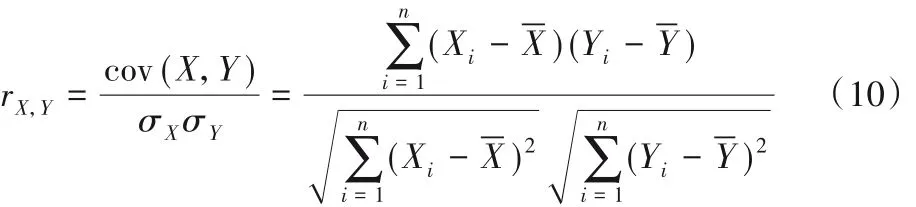
2.2 增量学习

增量学习对于流量数据的学习有重要意义，因为这些数据随着时间的变化在不断变化，且增长速度快。增量学习与人类学习过程相似，是指系统可以不断地从新数据中学习到新的知识，并能保存以前学过的旧知识。每当有新的数据到达时，模型不需要对所有的数据重新进行训练，仅仅需要对由于新增数据所引起的变化进行更新，其流程如图5 所示。利用增量学习思想，分类模型进行小的改动就能对新的数据进行训练，以较小的时间损耗达到模型更新的目的。

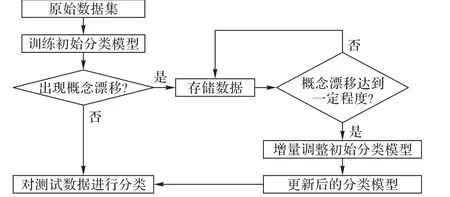
图5 增量学习流程Fig. 5 Flowchart of incremental learning

2.3 早期概念漂移检测

概念漂移普遍存在于机器学习领域，它是指随着时间的推移，目标概念的统计特性随着环境的变化而发生变化，导致模型的预测精度明显降低的现象［21］。在分类问题中，概念漂移体现为样本的属性特征与样本的类标识之间的映射关系的变化。从流样本X 到类标识C 之间的映射关系可以用映射函数H：X → C表示，即：

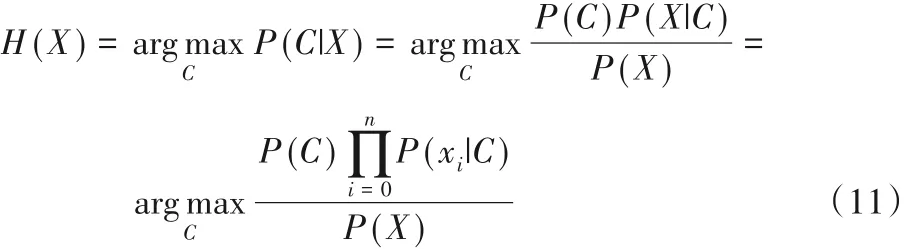
其中：P(C|X)为X发生的条件下C的后验概率；P(C)表示类别C 的先验概率；P(xi|C)为C 发生的条件下xi的后验概率；P(X)表示流样本X 的先验概率。由式（10）可以看出，P(C)、P(X)和P(xi|C)任何一个的变化，都会引起P(C|X)的变化，从而影响分类器的分类结果。

引入早期概念漂移检测方法（Early Drift Detection Method，EDDM）［22］，设定警示水平和漂移水平，结合错误分类之间的距离和错误分类的次数来判断系统的稳定性。

某个类别被错误分类的标准方差可以根据式（12）计算：

其中：pi′表示该类别被错误分类的概率。pi′可根据式（13）计算：

其中：DT(C)表示被错误识别的类别C的数量；T(C)表示数据集中类别C的数量。

当分类误差率（即错误分类概率pi′及其标准差si′之间的距离）明显增长时，表明样本分布出现了变化，已经不稳定，先前训练好的模型已经不适用于当前的样本。当pi′+ 2si′达到最大值时，pmax′+ 2smax′为分类错误分布距离最大的点，系统会存储值 pmax′和 smax′。

若存在：

称α 为警示水平。超出此级别之后，表明系统可能发生概念漂移，系统将在此时存储样本。

当：

称β 为漂移水平。一旦超过这个水平，就表示系统发生了概念漂移。系统将利用在警示触发时存储的样本训练新的模型，并重置pmax′和 smax′。

具体地，当模型至少发生30 个分类错误时，系统会根据之前设定好的漂移水平去检测模型是否发生了概念漂移，而在30 个分类错误发生的期间，系统可能已经存储大量样本。这里将分类错误次数设置为30 的原因是因为要估算两个连续错误之间的距离分布并将其与未来的分布进行对比，以此发现样本分布的变化。其中，pmax′+ 2smax′表示了95%的特征分布区间，α和β分别被设置为0.95和0.90。

2.4 基分类器的集成

在概念漂移的情况下，若用固定的模型去学习变化中的流样本，其分类精度定然不高，故本文采用以权值取代平均值的方式对基分类器进行集成［23］。集成分类器的计算公式如下：

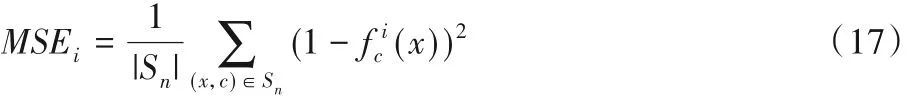
其中：|Sn|表示流样本的数目为样本(x，c)被错误分类的概率表示样本被正确分类的概率。

；1- f c

i(x)

假设分类器随机进行预测，实例x被分为c类的概率等于c的类分布p(x)，则分类器的随机均方误差为：

由于随机模型不包含关于数据的有用知识，因此使用MSEr，即随机分类器的错误率作为加权分类器的阈值。也就是说，丢弃误差等于或大于随机均方误差的分类器。分类器的权值计算公式如下：

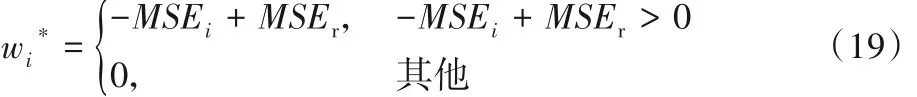
3 实验与结果分析

为了验证本文基于集成学习的网络流量分类模型的可行性，使用Moore 数据集进行实验，实验环境为Intel Core i5-7400 CPU @3.00 GHz，8.00 GB RAM，Windows 10 操作系统，Weka3.8.3，Python 3.6.5。

3.1 实验数据

Moore 数据集由 Moore 等［7］整理，特征维数高，数据量大，能依据统计信息准确判定网络流量所属的类别，是目前被用于网络流量分类研究最为权威的数据集，它的统计信息如表1所示。该数据集采集于拥有1 000名左右工作人员的研究机构，通过对该机构的研究设施进行24 h 全双工跟踪得到10 个原始数据集，每次记录时间约为28 min。Moore 数据集共有377 526 条流量样本，包含12 个类，每一条样本数据包括248个特征属性以及该网络流量所属类别的类别信息。

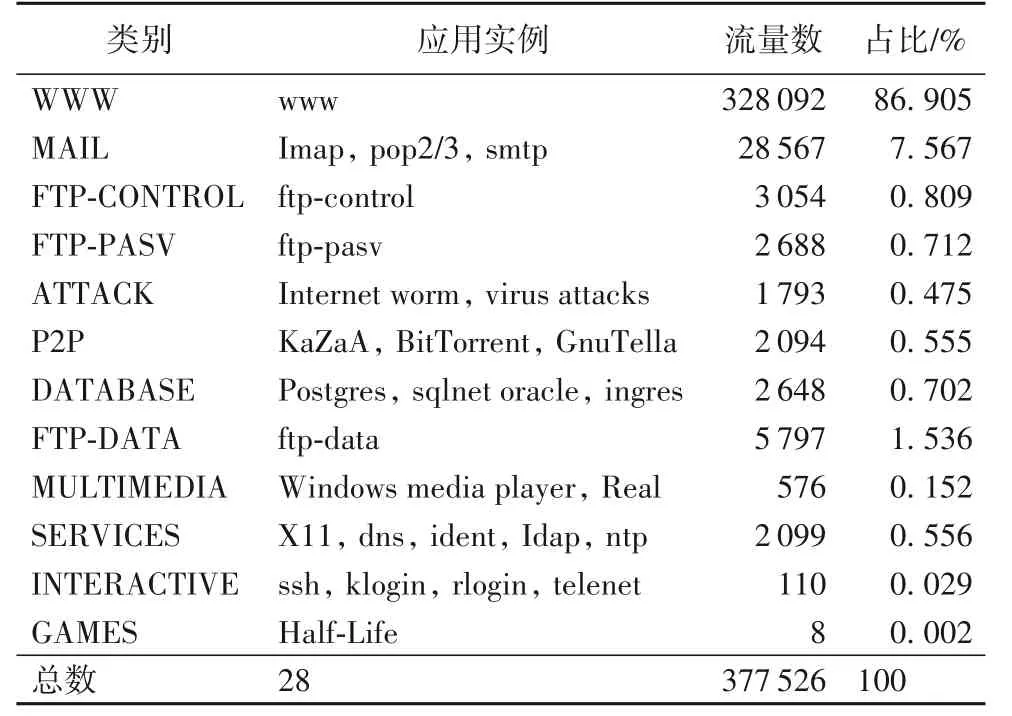
表1 实验数据集的统计信息Tab. 1 Statistics of experimental dataset

从表1可以看出，Moore 数据集各类别样本数量之间的差距非常大，大类（WWW 类）的样本占比高于85%，小类（例如FTP-PASV 类、ATTACK 类）的样本占比不足1%，是一个典型的类不平衡数据集。由于DATABASE、INTERACTIVE 和GAMES 这三类在某些数据子集中的样本条数为0，故在实验过程中删除了这三种类别的所有样本。

3.2 评价指标

在实验中，使用整体精确率（Accuracy）、准确率（Precision）、召回率（Recall）、F1 值和G-mean 值作为算法的性能评价指标。整体精确率反映了多分类模型的综合预测能力，准确率、召回率、F1值和G-mean值则可以反映多分类模型对单个应用的预测能力。

3.3 结果对比

3.3.1 WSU_AMB算法所选特征数目

WSU_AMB 特征选择算法的停止准则是找到满足合适维度的特征子集。特征数太少，可能漏选网络流量的典型特征；特征数太多，会造成资源的浪费，且有可能会把个性当成共性来学习，出现“过拟合”现象。一般来说，在对网络流量进行分类时，4～8个特征就可以很好地区分流量类型。利用Moore数据集的10 个子集进行实验仿真，发现有相似的变化趋势，故只选取两个数据集进行展示（Entry1、Entry2），如图6 所示，当所选特征数L= 6时，模型可以取得较好的分类精度。

3.3.2 ELTCM基分类器的选择

朴素贝叶斯（Naive Bayes，NB）算法学习和预测的效率很高，是一种常用的分类方法；逻辑斯蒂回归模型（Logistic Regression，LR）运算速度快、鲁棒性较好，是经典的分类方法；支持向量机（Support Vector Machines，SVM）具有较好的鲁棒性，可以有效解决分类情景中的高维问题；C4.5 决策树（Decision Tree，DT）能够处理多输出的问题，是多分类的常用算法。

利用 Moore 数据集的10 个子集（Entry1～Entry10）进行实验仿真，选择NB、LR、SVM和C4.5作为基分类器，以测试不同机器学习算法对ELTCM的分类精度的影响。

在Entry1 上，利用四种算法作为基分类器进行模型的训练，用训练好的模型对Entry2～Entry10 进行分类，其分类精度如表2所示。从表2中可以看出，NB算法的分类精度不高，平均分类精度只有85.52%，LR 算法的分类精度高于NB 算法，但低于 SVM 和 C4.5；SVM 和 C4.5 分类精度较高，均能达到90%以上，且稳定性好，分类精度的波动幅度较小，但相较于C4.5算法，SVM 算法无法直接用于多分类且不适用于大规模数据的训练，建模时间很长，会增加模型更新时间，故选择C4.5算法作为本文模型的基分类器。

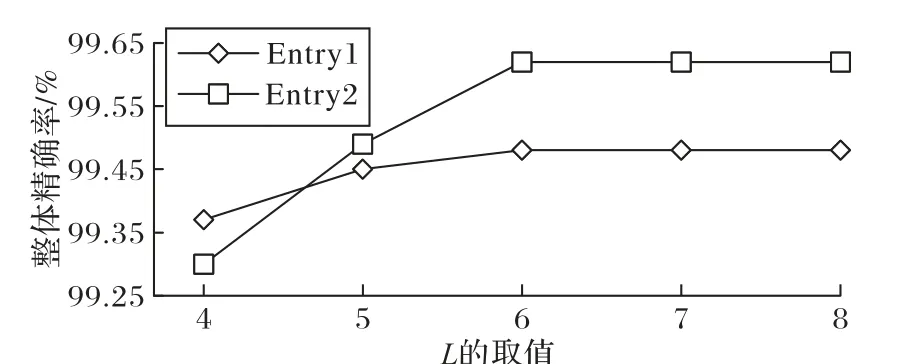
图6 L值对分类模型的影响Fig.6 Impact of L value on classification model

3.3.3 分类模型的对比

文献［8］中提出的模型首次将贝叶斯神经网络（Bayesian Neural Network，BNN）引入流量分类领域，可以获得较好的分类效果，给研究人员带来了巨大的启发；基于C4.5 决策树的分类模型（Internet Traffic Classification based on C4.5 Decision Tree，DTITC）［9］在处理大规模流量分类问题时，具有较好的优势；基于流量统计特征的分类模型（Internet traffic classification based on Flows’Statistical Properties with Machine Learning，FSPML）［18］能够识别新的应用，可以得到较高的分类准确率；基于错误率的概念漂移检测分类模型（Classification model for concept Drift Detection based on Error Rate，ERCDD）能降低概念漂移带来的影响，提升模型的分类性能。

将本文模型 ELTCM 与 BNN、DTITC、FSPML 和ERCDD 进行对比，利用Entry1 按照训练集和测试集为7∶3 的比例生成分类器，用基于Entry1 生成的分类器对Entry1～Entry10 进行分类。

各模型的分类整体精确率如图7 所示，可以看出，五种模型的整体精确率均超过98%，ELTCM 的平均整体精确率最高，可以达到99.62%。各模型在Entry1上都能得到较高的整体精确率，而BNN、DTITC 和FSPML 模型在Entry2～Entry10 上的分类整体精确率却出现了下降，且随着时间的推移，模型分类精度下降趋势越来越明显，说明概念漂移对模型的分类性能有较大影响，即在一个数据集上训练得到分类器，利用该分类器对该数据集进行分类时，能得到较好的分类结果；而利用该分类器去分类时间上相邻的其他数据集时，分类精度会出现下降的趋势。ERCDD 模型的平均整体精确率为99.26%，仅次于ELTCM，整体精确率的波动小于BNN、FSPML 和DTITC 三种模型，说明该模型能在一定程度上减少概念漂移的影响，但其波动幅度大于ELTCM。ELTCM 的整体精确率在9 个数据集上达到最高，整体精确率的波动幅度不超过0.13%，具有较高的稳定性，说明该模型能有效应对概念漂移现象。

从 3.1 节可以得知，删除 DATABASE、INTERACTIVE 和GAMES 三类之后，FTP-CONTROL（简称 FTP-C）、FTP-PASV（简称FTP-P）、ATTACK、P2P、MULTIMEDIA（简称MULT）和SERVICES（简称SERV）这6 类网络流量在数据集样本中所占比例不足1%，相较于WWW 所占的86.905%，这6 种类型均属于小类。选择这6 类应用对五种分类模型在小类别上的性能进行分析，考察不同分类模型对小类别的预测能力。

同样的，利用Entry1 按照训练集和测试集为7∶3 的比例生成分类器，用基于Entry1生成的分类器对Entry1～Entry10进行分类，可以得到各模型在每个应用类别上的分类性能，对10个子集取平均值，结果如图8所示。

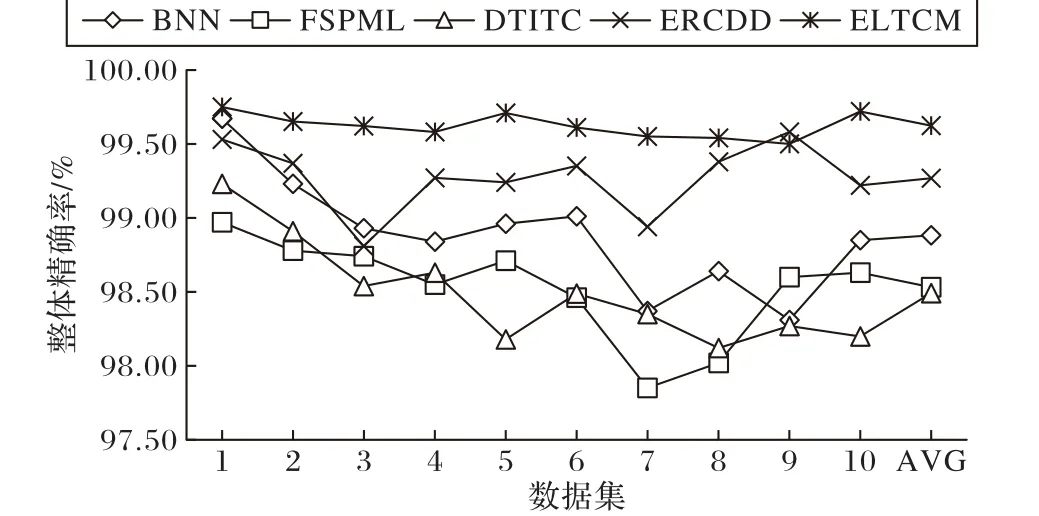
图7 不同分类模型的整体精确率对比Fig. 7 Comparison of overall accuracy between different classification models

Precision 表示被预测为类别C 的样本中，实际属于类别C的比例，从图 8（a）可以看出，ELTCM 在 5 个小类别上的平均Precision 均高于对比算法，MULT 类的平均准确率也仅比ERCDD 模型低0.07%，说明ELTCM 能更为精准地识别小类别。Recall 衡量了某个类别的所有样本被正确识别的比例，从图8（b）可以看出，ELTCM 在小类别上有较好的查全率。F1值是Precision 和Recall 的综合评价指标，更高的F1 值表示更好的分类效果，从图8（c）可以看出，ELTCM在6种小类别上的F1 值均有所提升，说明ELTCM 的分类效果更好。G-mean 值是衡量不平衡分类问题的有效指标，G-mean 值越大，表明分类效果越好，从图8（d）可以看出，ELTCM 可以取得较高的G-mean 值，能有效应对类不平衡问题。相较于对比算法，ELTCM 在绝大多数小类别的分类性能上都存在明显优势，这是因为 BNN、FSPML、DTITC 和 ERCDD 模型以整体分类精度为目标，多数类在分类过程中占优势，忽略了小类别的分类性能，且BNN、FSPML 和DTITC 模型未考虑概念漂移现象，ERCDD 模型仅仅基于错误率进行概念漂移检测，不能很好地应对渐变型概念漂移。综上，ELTCM 在综合评价指标和单个应用的评价指标上取得了较好的结果，均优于对比模型，验证了本文模型的有效性。

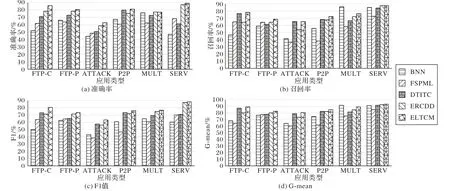
图8 不同分类模型的小类别分类性能对比Fig.8 Comparison of classification performance of minority classes among different classification models

4 结语

本文通过对传统基于机器学习的流量分类模型的分析，针对传统模型难以实现频繁、及时的更新，忽略了网络流量样本分布不平衡的问题，提出了一种基于集成学习的网络流量分类模型。该模型引入了偏向于小类别的特征度量——加权对称不确定性，利用基于WSU_AMB 的特征选择算法选择最优特征子集，将所选特征输入集成分类器系统，采用增量学习的方式进行网络流量分类训练，提升模型的泛化能力，并对模型进行早期概念漂移检测，优化网络流量分类模型性能。利用公开数据进行验证，实验结果表明本文提出的分类模型能有效减小概念漂移问题带来的影响，可以在保证整体分类准确度的前提下，提高小类别的识别率。如何识别加密流量以及运用未标注流量进行分类是下一步的主要研究内容。