基于混沌搜索和错卦变换的阴阳平衡优化算法

许秋艳，马 良，刘 勇

（上海理工大学管理学院，上海200093）

0 引言

近年来，智能优化算法得到了快速发展，出现了许多有代表性的方法。例如，遗传算法（Genetic Algorithm，GA）、神经网 络（Neural Network，NN）、蚁 群 优 化（Ant Colony Optimization，ACO）算 法 、粒 子 群 优 化（Particle Swarm Optimization，PSO）算法、人工蜂群优化（Artificial Bee Colony Optimization，ABCO）算法、模拟退火（Simulated Annealing，SA）算法、量子优化（Quantum Optimization，QO）算法、禁忌搜索（Tabu Search，TS）算法和差分进化（Differential Evolution，DE）算法等［1-4］。之所以存在这么多的智能优化算法，是因为根据无免费午餐定理［5］，一种算法无法解决所有问题，需要设计不同的求解算法来解决各种各样的问题。绝大多数智能优化算法是根据生物学原理或者物理学原理所蕴含的优化机制进行设计的［6-8］。也正因为此，受到自身优化机制的限制，这些算法在实际应用中会或多或少暴露出其固有的一些缺陷［9-12］。智能优化算法的设计需要从对生物学原理或者物理学原理的模拟扩大到更大的范围。

阴阳是中国最古老的哲学观念之一，如《易经・系辞上》中“一阴一阳之谓道”。阴阳最初涵义是表示阳光的向背，向日为阳，背日为阴，后引申为寒与热、上与下、动与静等。一般来说，外向的、上升的、温热的，都属于阳；内守的、下降的、寒冷的，都属于阴。阴和阳二者既相互对立，又相互依存。阴阳之间这种互相依存的关系，称之为阴阳互根。而对立互根的阴阳双方，并不是处于静止不变的状态，而是始终处于不断的运动之中，有阴阳互为消长、阴阳皆长和皆消等变化形式。而阴阳平衡就是阴阳双方的变化保持协调，呈现一种和谐的状态。“阴平阳秘”就是对这种理想状态的概括［13］。

受到阴阳学说的启发，印度学者 Punnathanam 等［14］于2016 年提出了阴阳平衡优化（Yin-Yang-Pair Optimization，YYPO）算法，源自对全局探索和局部开发平衡的模拟。在智能优化算法中，全局探索和局部开发是必备的两个组成部分：全局探索主要目的是对算法空间进行更全面的搜索，希望发现更多的未知区域；而局部开发主要目的是对已知区域进行更为精细的搜索，希望获得质量更好的新解［15-17］。而在有限的计算时间内，如何实现全局探索和局部开发的平衡一直是智能优化算法设计中极具挑战性的问题。YYPO 算法则将全局探索和局部开发的均衡视为阴阳平衡的一种实现形式。

在YYPO 算法中，首先随机产生两个初始点。其中，适应度值较好的点用P1表示，适应度值较差的点用P2表示。然后以P1为中心、δ1为步长在半径为1 的超球体内进行搜索。对点P2，设置步长δ2，进行同样的上述操作。在上述过程中，搜索步长δ1将逐渐变小而δ2将逐渐增大。因此，基于点P1的优化搜索范围会逐步缩小而进行精细化寻优，在YYPO 算法中称之为局部开发，含有向内收缩之义，和阴相对应；而基于点P2的优化搜索范围会逐步变大而对更多未知区域进行寻优，在算法中称之为全局探索，含有向外扩张之义，和阳相对应。基于点P1的局部开发和基于点P2的全局探索是算法两个必备的组成部分，含有阴阳互根之义。基于点P1的优化搜索要求在较小的区域内进行，而基于点P2的优化搜索要求在较大的区域内进行，含有阴阳对立之义。在整个优化过程中，基于点P1的局部开发和基于点P2的全局探索的强度不断增加，含有基于互根的阴阳皆长（阴阳消长的一种形式）之义。算法不断重复上述优化过程，期望实现全局探索和局部开发的均衡，含有阴阳平衡之义。

YYPO 算法自提出以来就备受研究人员的关注。文献［18］中提出了一种简化版的YYPO 算法；文献［19］中提出了一种自适应YYPO 算法；文献［20］中提出了一种混合YYPO算法等。这些新方法为YYPO 算法的研究提供了参考，但是算法在求解复杂困难的优化问题时容易早熟收敛，优化潜力有待进一步提高［18-21］。

现有研究表明，只有进一步增强全局探索和局部开发能力，才能提高YYPO算法的优化性能［18-21］。从算法设计角度考虑，利用混沌可以提高算法的全局探索能力。和阴阳学说一样，混沌思想也是中国传统文化重要组成部分。在中国古代宇宙生成论中，混沌是个重要阶段，有所谓“混沌初开，乾坤始奠。”混沌关于宇宙生成阶段的描述是指一种原始未分化的状态，包含一切可能性的状态。而在智能优化算法中，基于混沌的遍历性等性质，混沌搜索已经成功用于优化算法设计中。本文也将混沌搜索引入YYPO 算法中，利用混沌的遍历性扩大对未知区域的搜索范围，提高算法全局探索能力。此外，同样从智能优化算法设计角度分析，《易经》的卦象变化也蕴含了优化思想。和阴阳学说类似，阴阳也是《易经》最核心的概念。《易经》的卦象就建立在阴阳变化的基础之上。例如，本卦的错卦就是阴阳爻互换，易理是看待问题可以从相反的角度来分析。与此类似，当算法陷入局部极值时，可以对当前解的反向解进行集中优化搜索，提高算法的局部开发能力。同时根据文献［21］中的研究，当前解有50%的概率比其反向解更远离最优解。在本文的算法设计中，错卦变换将通过反向学习（Opposition-Based Learning，OBL）策略实现。本文提出了基于混沌搜索和错卦变换的YYPO（Yin-Yang-Pair Optimization based on Chaos Search and Intricate Operator，CSIOYYPO）算法，通过大量标准测试函数进行数值实验的结果表明，该算法具有更高的计算精度和更快的优化速度。

1 基本YYPO算法

受太极图（图1）启发，YYPO 算法的搜索空间为半径为1的超球体。点P1和P2的搜索范围限制在0到1之间。在对P1和P2两个点进行随机初始化后，利用P1和P2两个点进行优化搜索。其中，基于点P1的搜索对应局部开发，而基于点P2的搜索对应全局探索。

图1 太极图Fig. 1 Taiji diagram

算法在具体实现时，主要包括基于超球体的解更新和基于归档集的解更新两个部分［14］。以下给出这两个部分所采用的主要方法。

1.1 基于超球体的解更新

算法在解的更新时，分别以 P1和 P2为中心、δ1和 δ2为步长在超球体内进行搜索。因为基于点P1和P2的更新方法相同，方便起见，令P表示待更新的点，δ表示步长。将待更新的点 P 进行复制，产生 2D 个相同的点，分别用 NP1，NP2，…，NP2D表示。其中，D 表示变量维数。更新方法主要分为点的一个分量更新和所有分量更新两种方式。点的一个分量更新方法如下：

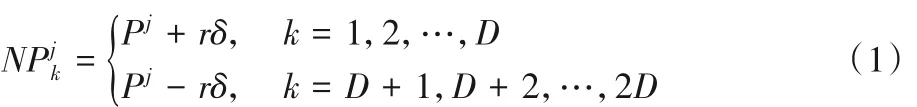
在进行点的全部分量更新时，还要生成一个规模为2D ×D 的二进制矩阵B，并且要求每一行对应的二进制串互不相同。以下给出点的全部分量的更新方法：

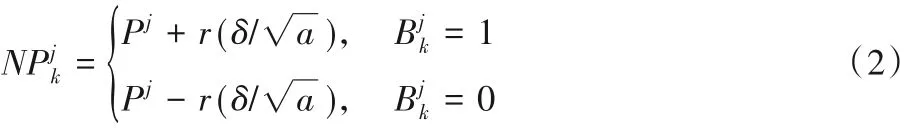
在进行基于P1和P2两个点的优化搜索时，点的一个分量更新方法和所有分量更新方法都以相同的概率（50%）被选择。如果产生的新分量取值范围在区间[0，1]之外，那么将其在0 到1 之间随机取值。此外，在产生新的点后，为计算其适应度函数值，需要将其映射到问题的解空间，具体方法如下：

基于点P1产生的2D 个新解中，选择适应度函数值最好的点，不管其是否优于P1都用其替换P1。类似的，基于点P2产生的2D 个新解中，也选择适应度函数值最好的点直接替换P2。

1.2 基于归档集的解更新

在基于超球体的解更新阶段中，基于P1新产生的适应度值最好点可能会劣于P1，对P2也会出现相同的情况。为保留当前最好的P1和P2，算法在基于超球体的解更新阶段前，将这两个点保存在归档集archive 中。在算法迭代过程中，每隔I代就利用归档集中保存的2I个点对P1和P2两个点进行更新。其中：参数I表示更新频率，且I在区间[Imin，Imax]内随机产生；Imin和Imax为预设的整数，并要求Imin＜Imax。

基于归档集的更新阶段实际上采用的是精英保留策略，最好的解能够被保留并用于引导后续的搜索。具体方法如下：首先从归档集中选择适应度值最好的点，并用Q1表示，如果Q1优于P1，那么两个点交换取值；然后继续从归档集剩下的点中选择适应度值最好的点，并用Q2表示，如果Q2优于P2，那么两个点也交换取值；最后，在该段结束前，将归档集清空，并重新生成更新频率I。

在该阶段，还需要对搜索步长δ1和δ2进行动态调整，具体方法如下：

其中：α是收缩/扩张因子；δ1是点P1的搜索步长，δ2是点P2的搜索步长。

基于点P1的优化搜索对应局部开发，在迭代过程中参数δ1取值逐渐递减，有利于点P1在较小的范围内进行精细搜索，有助于算法发现质量更好的解；基于点P2的优化搜索对应全局探索，在迭代过程中参数δ2取值逐渐递增，有利于点P2在较大的范围内进行广域搜索，有助于算法发现质量更好的解区域。但是为防止参数δ2无限增加，越过算法搜索空间的边界，将其上限设为固定值

2 基于混沌搜索和错卦变换的YYPO算法

YYPO 算法独特的搜索机制为智能优化算法的研究提供了新的思路。但是基本算法在求解复杂困难的优化问题时容易早熟收敛、陷入局部极值［18-21］。为解决上述问题，本文引入混沌搜索和错卦变换，以进一步提高算法的全局探索和局部开发能力。

2.1 基于混沌搜索的优化策略

在YYPO 算法中，影响基于P2的全局探索能力的主要因素有搜索步长δ2和随机变量r。算法通过不断扩大搜索步长δ2，期望对更多的解区域进行搜索，不断提高点P2的全局探索能力；但是随机变量r不具有遍历性，无法覆盖所有的解区域。

从智能优化算法设计角度分析，混沌具有遍历性，可以提高算法的全局探索能力；而在智能优化算法领域，基于混沌的遍历性已经得到成功应用。基于此，本文算法将引入混沌搜索。

本文算法将混沌搜索引入到YYPO 算法中的第一个阶段，即基于超球体的解更新阶段。该阶段主要由式（1）、（2）组成，在这四个迭代方程中都存在随机变量，即在[0，1]区间服从均匀分布的随机变量r。新算法将采用混沌变量替换随机变量，基于混沌的遍历性对解空间进行搜索，提高算法的优化性能。

Logistic 映射是混沌动力学中一种常见模型，其数学表达式为：

他反反复复地练习滑翔，早早便成为了云浮“飞”得最远的人。但那种借助外物机械带来的飞行体验，又怎能满足得了他的心呢？他无数次地坐在山巅，仰望无尽的苍穹，望着云浮山上空飞过的雄鹰和鸿雁，望着云浮山下飞过的雨燕和黄鹂，他无数次地想，如果能飞一次，哪怕只有一次，此生也便无憾事了。

Logistic映射对应的迭代方程为：

其中：xk表示混沌变量在第k次迭代时的取值；μ为控制参数，且μ∈ [0，4]。在设计优化算法时，混沌变量由式（7）产生。对于给定的μ和x0，迭代序列x1，x2，…，xn组成xk→xk+1的映射运算。

通常情况下，正的Lyapunov 指数意味着混沌。当μ∈ [3.569 945 672，4]时，Lyapunov 指数为正数，系统呈现混沌状态；当μ= 4时，Lyapunov指数达到最大值0.69，系统处于完全混沌状态。

在利用Logistic 映射产生混沌变量进行优化搜索时，首先对式（9）中的x0赋初始值（不能取Logistic 映射的不动点：0.25，0.5 和0.75）。然后根据式（7），计算产生的混沌变量xk。如果进行一个分量更新，每次需要产生2D个混沌变量；如果进行所有分量更新，每次需要产生2D×D混沌变量。

另外，需要指出的是混沌还有规律性和随机性等特点。规律性是指混沌可以由确定型迭代方程产生，这将为优化算法设计提供有利条件；混沌的随机性则是指对于初始条件极其敏感，初始条件的微小变化可导致轨道按照李雅普诺夫指数方式迅速分离。因此，将混沌搜索引入YYPO 算法中，初始条件的设置会对算法的优化性能产生一定影响。

2.2 基于错卦变换的优化策略

除利用混沌搜索提高全局探索能力外，算法的局部开发能力也需要进一步提高。YYPO 算法在利用点P1进行局部开发时，易陷入局部极值［20］。如何增强局部开发能力、跳出局部最优一直是智能优化算法领域的研究热点。对智能优化算法而言，《易经》的卦象变化同样蕴含了优化思想，可以为算法设计提供借鉴。例如一卦共有六爻，在爻的位置不变的情况下，通过“阴变阳、阳变阴”的法则，得出的另一卦叫错卦。例如图2（其中，“—”表示阳爻，“--”表示阴爻），乾卦变作坤卦，坤卦就是乾卦的错卦；同时，乾卦也是坤卦的错卦。错卦的理是立场相同，目标一致，但从相反的角度看问题。

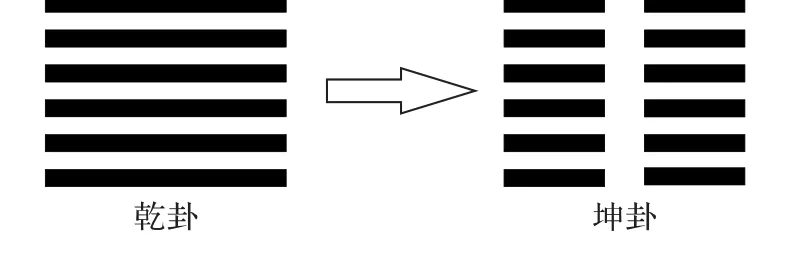
图2 错卦变换示意图Fig. 2 Schematic diagram of intricate operator

与错卦变换类似，当算法陷入局部极值时，可以考虑采用当前解的反向解进行优化搜索。文献［22］中的研究表明，当前解有50%的概率比其反向解更远离最优解。

基于《易经》的错卦变化规则，可以采用反向学习策略实现。反向学习策略由Tizhoosh 在2005 年提出，在优化领域已经得到成功应用［22］，其基本原则是同时考虑变量的当前值与其反向值，并通过比较获得该变量的最优取值。Rahnamayan等［22］对反向学习策略进行理论分析，研究表明采用反向学习策略生成当前解的反向解，能够充分挖掘出反向解中的优化信息，有助于提高算法局部开发性能，以更大的概率逼近全局最优解。通过预研，本文采用基于形心的反向解学习策略。具体方法如下：

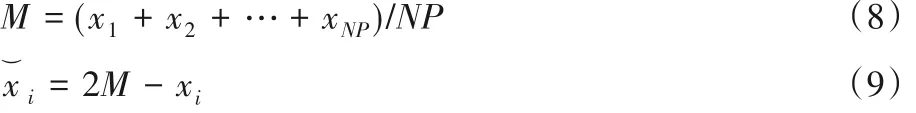
综上所述，给出基于混沌搜索和错卦变换的YYPO 算法的主要计算步骤如下：

步骤1 对P1和P2两个点进行随机初始化。

步骤2 计算点P1和P2对应的适应度函数值。

步骤3 若点P1对应解优于点P2对应解，则互换两个点的取值和对应搜索半径。

步骤4 在基于超球体的解更新阶段，以等概率方式分别对点P1和P2进行混沌搜索。

步骤5 基于错卦变换机制，采用基于形心的反向解学习策略。

步骤6 若间隔的迭代次数等于更新频率I，则采用基于归档集的解更新策略；否则，转步骤7。

步骤7 若满足算法停止条件，则输出当前最优结果；否则，转步骤2。

3 数值实验与分析

为验证本文CSIOYYPO 算法的性能，首先将其与基本YYPO 算法以及自适应阴阳平衡（Adaptive Yin-Yang Pair Optimization，AYYPO）算法进行比较；然后将CSIOYYPO 算法和PSO 算法、引力搜索算法（Gravitational Search Algorithm，GSA）和布谷鸟搜索（Cuckoo Search，CS）算法等其他类型智能优化算法进行比较。所有算法在Windows 10 下，采用Matlab（R2016b）编程实现。采用13 个标准测试函数［22］进行数值实验，这些函数的具体定义如下：

搜索范围为[-100，100]，最优值为0。

搜索范围为[-10，10]，最优值为0。

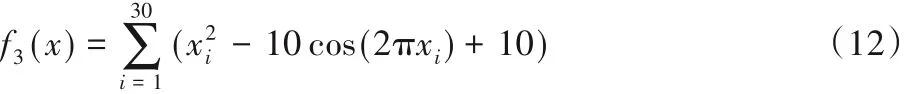
搜索范围为[-5.12，5.12]，最优值为0。

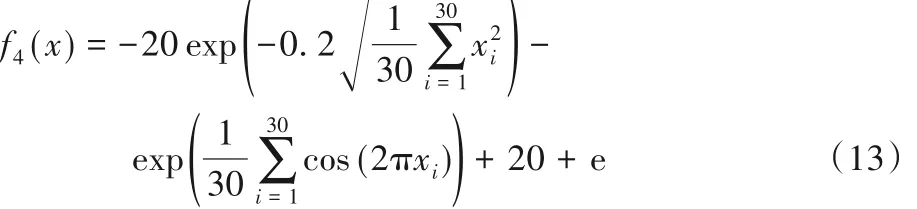
搜索范围为[-32，32]，最优值为0。

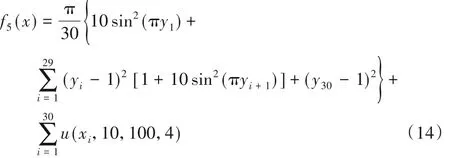
其中：

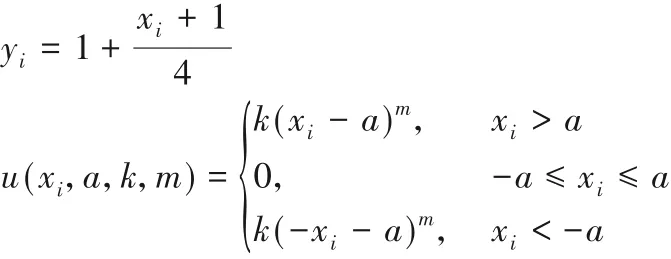
搜索范围为［-50，50］，最优值为0。

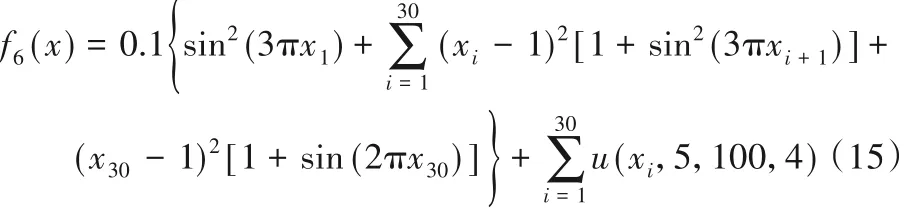
搜索范围为［-50，50］，最优值为0。

搜索范围为［-1.28，1.28］，最优值为0。

搜索范围为［-10，10］，最优值为0。

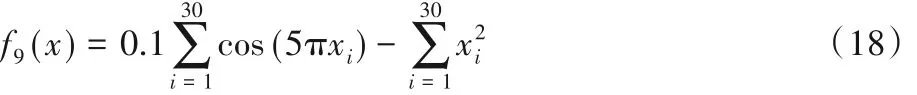
搜索范围为［-1，1］，最优值为-3。

搜索范围为［-5，5］，最优值为0。

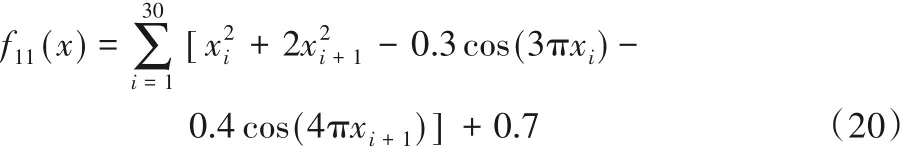
搜索范围为［-15，15］，最优值为0。

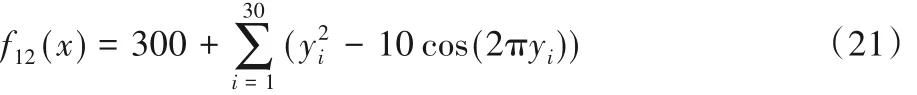
其中：

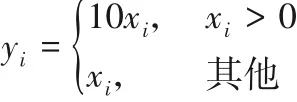
搜索范围为[-5，5]，最优值为0。

搜索范围为［-1，1］，最优值为0。

3.1 算法并行程序设计

绝大多数智能优化算法属于随机优化方法，同一个算法需要多次运行，统计其平均性能。为减少计算时间，可以对算法进行并行程序设计。此外，计算机都配备了双核、四核甚至十六核的CPU，在体系结构方面已具备了实现并行计算的硬件条件。目前，许多编程语言都支持多核并行编程。例如，Matlab 提供的并行计算工具箱（Parallel Computing Toolbox），可以利用parfor对for循环结构进行并行化。

以CSIOYYPO 算法求解f1为例，比较并行和串行的计算时间差异。算法参数设置为：Imin= 1，Imax= 2，a = 2 和α = 25；此外，δ1和 δ2的初值均为 0.5，δmax2= 0.75。需要指出的是，混沌搜索对初始值比较敏感。在实验中根据文献［3］中的研究结论，控制参数μ = 4 且初始值x0= 0.202 7。每次最大迭代次数为4 000，循环次数为10。由于Matlab 并行计算工具箱已经隐藏了多进程和多线程操作，故而可直接利用parfor对for 循环进行并行计算。所有数值实验均在CPU 为Intel Xeon E-2186M、32 GB 内存、2.90 GHz 主频的工作站运行。在实验时，调用6 核进行并行计算。实验发现，for 循环耗时231.310 909 s，而parfor 循环仅耗时58.465 434 s。为进一步比较parfor 和for 两种循环计算时间的差异，循环次数从1 增加到50，运行时间对比如图3 所示。从图3 可以发现，当循环次数为1 时，parfor 和for 两种循环计算时间差不多；但是随着循环次数的增多，parfor循环计算时间显著减少，通过parfor实现的程序并行执行提高了运行效率。基于此，本文所有算法均采用parfor循环结构进行并行程序设计，以提高计算效率。

3.2 与同类型YYPO算法比较

为验证CSIOYYPO 算法能否提高搜索性能，首先将其与基本YYPO 算法以及AYYPO 算法的实验结果进行比较。为公平起见，三种算法设置相同的函数评价次数480 000。本文算法参数设置不变，基本YYPO 算法和AYYPO 算法的参数分别根据文献［17］和［19］进行设置。三种算法分别运行200次，每次运行时算法设置相同的初始解。分别统计最优值、最差值、平均值和标准差等指标，实验结果如表1所示。

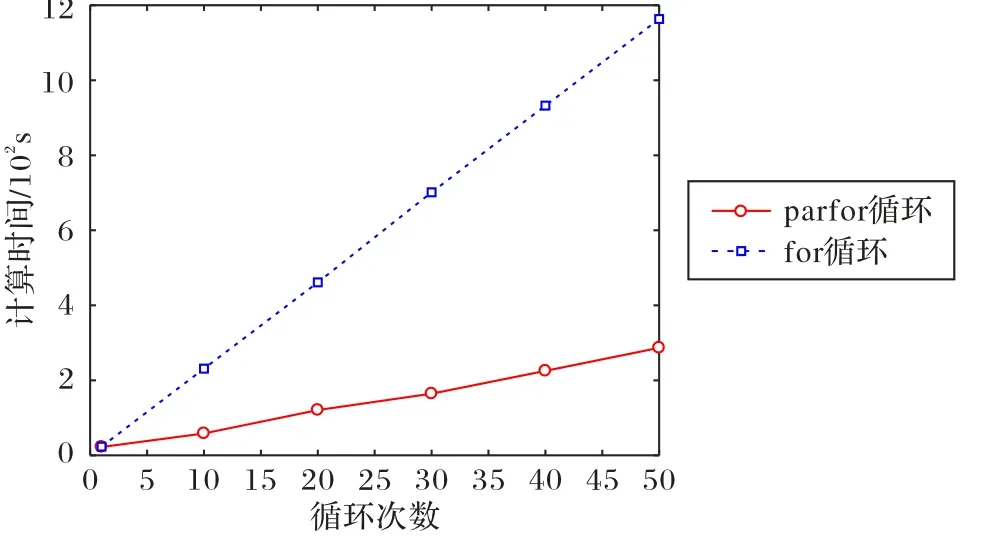
图3 parfor和for两种循环计算时间对比Fig. 3 Calculation time comparison between parfor and for loops

由表1 可知：CSIOYYPO 算法对11 个函数（包括f1、f2、f3、f4、f5、f6、f7、f8、f11、f12和f13）的结果显著优于YYPO 算法，对12 个函数（包括f1、f2、f3、f4、f5、f6、f7、f8、f10、f11、f12和f13）的结果明显优于 AYYPO 算法。尤其对f2和f11，CSIOYYPO 算法能够收敛到理论最优值，且标准差为零。对f9而言，三种算法都获得了相同的最优值、最差值和平均值，但是CSIOYYPO 算法的标准差稍劣于YYPO 算法和AYYPO 算法。对f10而言，YYPO 算法在最优值方面具有一定的优势，而CSIOYYPO 算法在最差值、平均值和标准差三个方面优势显著。

综上所述，在同样的评价次数下，CSIOYYPO 算法具有更高的计算精度。此外，对绝大多数测试函数，CSIOYYPO 算法的标准差是最小的，说明算法的稳定性是最好的。为进一步比较这三种阴阳平衡优化算法的优化速度，部分函数的寻优过程对比如图4 所示。由图4 可以看出，相较YYPO 算法和AYYPO 算法，CSIOYYPO 算法不仅具有更高的计算精度，而且具有更快的优化速度。基于传统文化中混沌概念引入的混沌搜索、以及《易经》中错卦变换引入的反向学习策略能够提高YYPO 算法的搜索性能。混沌搜索充分利用其遍历性对更多的未知区域进行广度搜索，提高算法的全局探索能力；在此基础上，根据反向学习策略，一个解有50%的概率不如其反向解优秀，算法对当前解的反向解进行集中搜索，以提高算法的局部开发能力，并加快优化速度。混沌搜索和反向学习策略可以更好地实现算法全局探索和局部开发的平衡。

3.3 不同类型的智能优化算法的对比

为进一步测试CSIOYYPO 算法的性能，将它与PSO、GSA和CS 等其他类型智能优化算法进行比较。CSIOYYPO 算法参数设置保持不变，其他三种算法分别采用文献［17，24-25］中参数设置。这四种算法仍然采用并行程序设计，每种算法分别独立20 次，统计最优值、最差值、平均值和标准差等指标，实验结果如表2 所示。由表2 可以看出：与其他类型的智能优化算法相比较，本文的CSIOYYPO 算法依然占有较大的优势，在绝大多数测试函数上都获得了更优的计算效果，算法计算精度更高。

图5 给出了这四种算法部分函数寻优过程对比。从图5可以看出，与 PSO 算法、GSA 和 CS 算法等相比较，CSIOYYPO算法不仅具有更高的计算精度，而且具有更快的优化速度。智能优化算法的核心是有效权衡全局探索和局部开发。如果算法没有引入有利于全局探索和局部开发平衡的策略，那么算法的优化性能较差，易陷入局部极值。本文算法仍然能够获得最好的优化效果，主要是因为：引入混沌搜索对更多区域进行探索，提高了全局探索能力；同时基于错卦变换引入反向学习策略，对当前解的反向解进行集中搜索，提高了局部开发能力，有效地协调了算法的探索与开发能力，确保在整体上能够提高算法的优化性能。

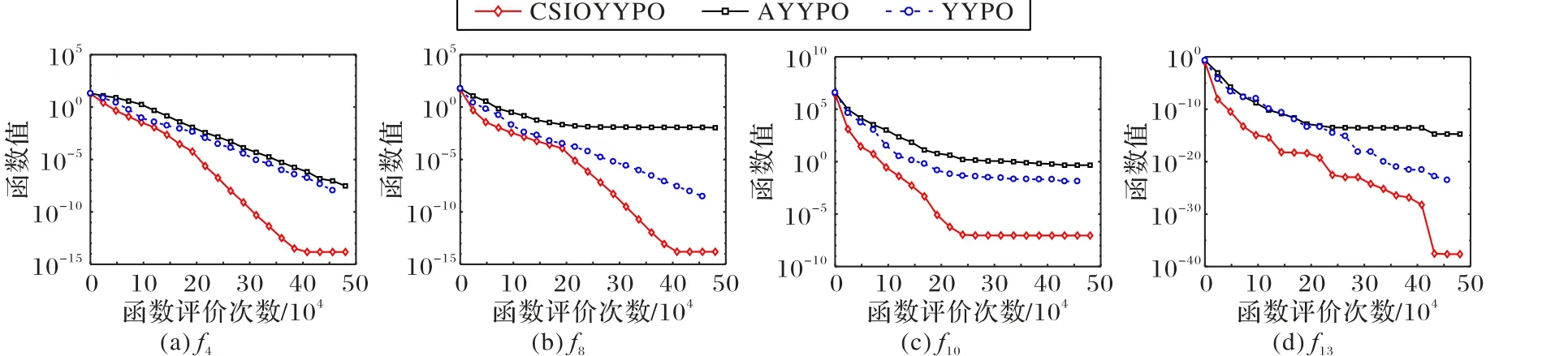
图4 三种YYPO算法寻优过程对比Fig.4 Optimization process comparison of three kinds of YYPO algorithms

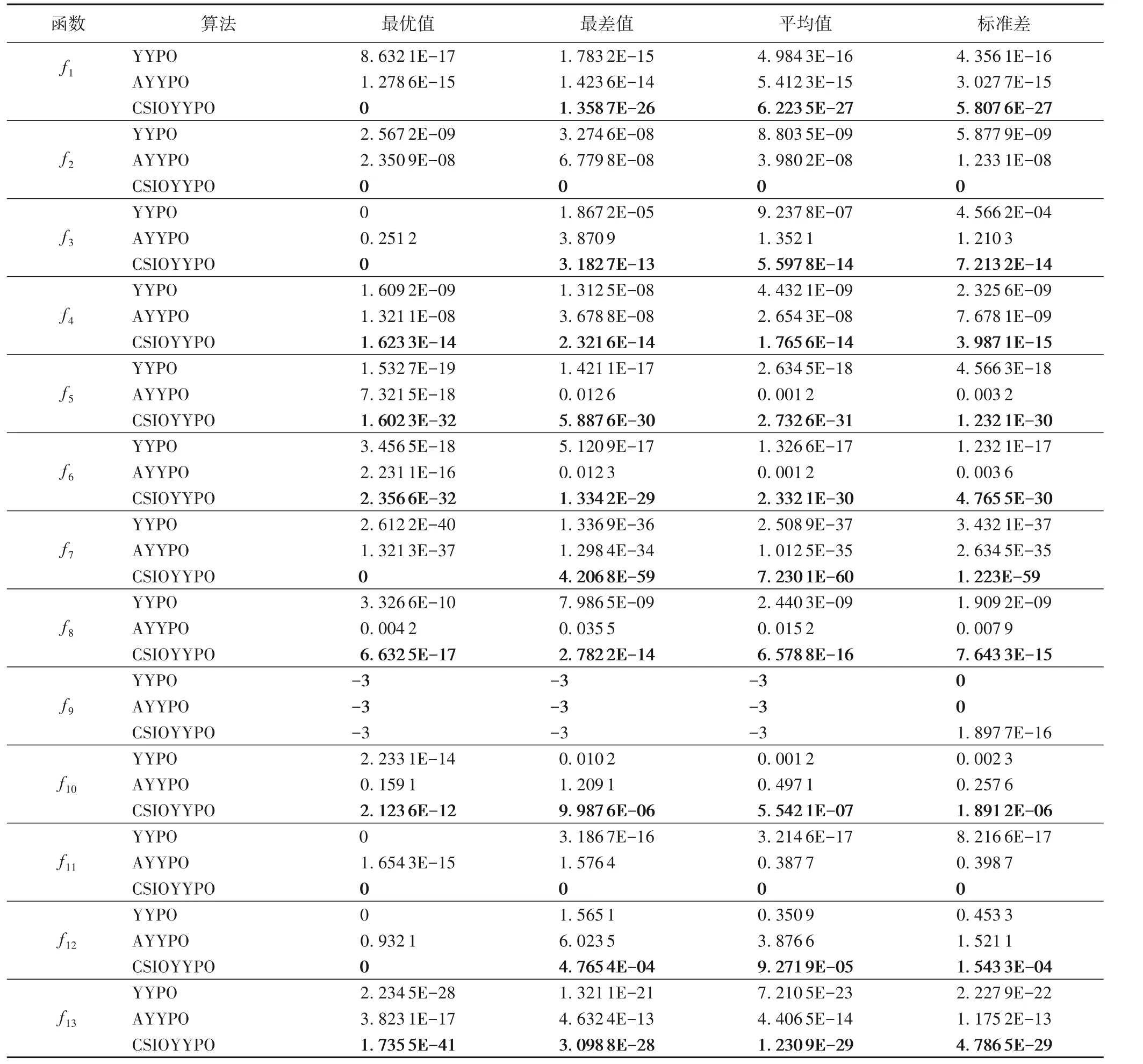
表1 三种YYPO算法的实验结果Tab. 1 Experimental results of three kinds of YYPO algorithms

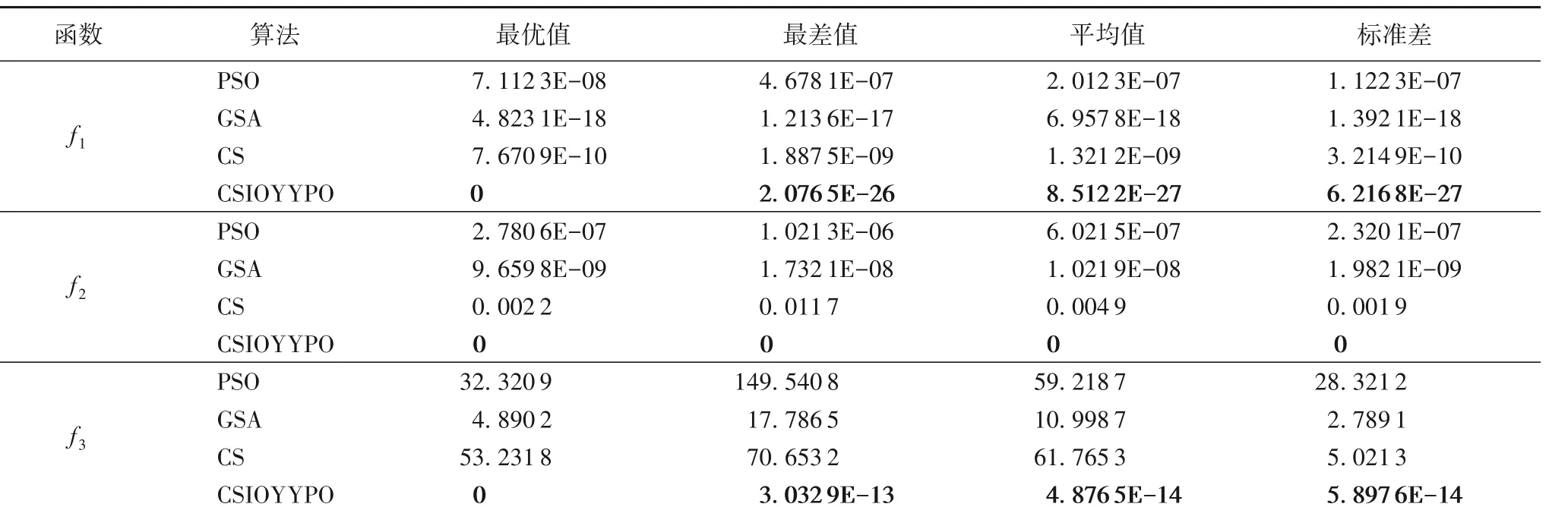
表2 不同类型智能优化算法的实验结果Tab. 2 Experimental results of different intelligent optimization algorithms

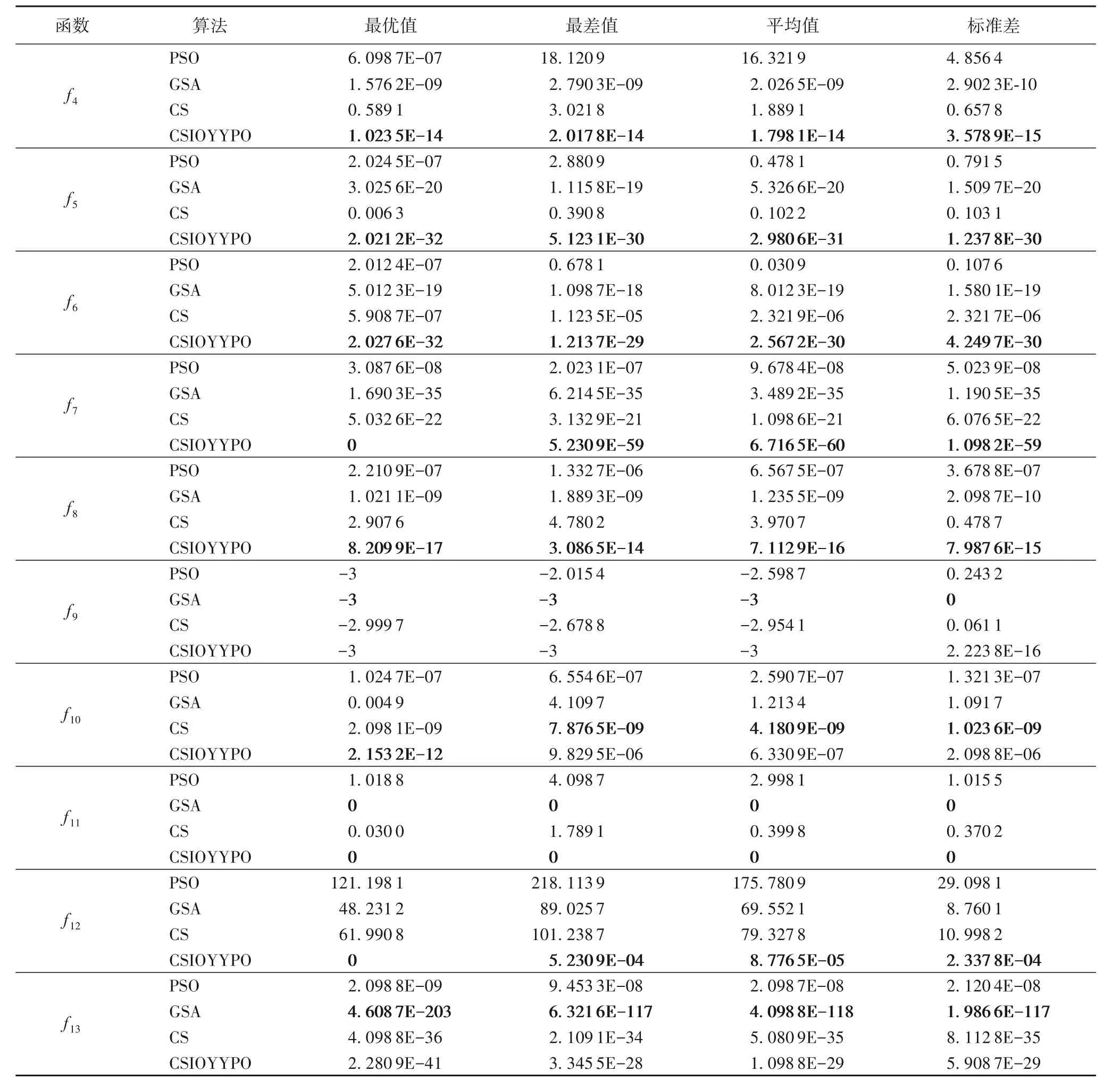
续表

4 结语

源于阴阳学说的阴阳平衡优化算法为智能优化算法设计提供了独特视角，也开启了弘扬传统文化的新途径。为解决基本YYPO 算法早熟收敛等问题，基于混沌的遍历性，将混沌搜索引入到算法中，对更多区域进行搜索以提高算法全局探索能力；基于错卦变换引入反向学习策略，对当前解的反向解进行集中搜索以提高局部开发能力。为充分利用多核处理器计算资源，算法采用并行程序设计，提升计算速度。大量的数值实验结果表明，新算法不仅具有更高的优化精度而且具有更快的搜索速度。将五行等中国传统文化融入YYPO 算法设计中是进一步的研究工作。此外，将算法用于多目标优化也是下一步的工作。