移动边缘计算中基于粒子群优化的计算卸载策略

罗 斌 ，于 波

（1. 中国科学院大学，北京100049； 2. 中国科学院沈阳计算技术研究所，沈阳110168）

0 引言

5G 具有近邻性、低延迟、高带宽等特性，作为关键技术的移动边缘计算（Mobile Edge Computing，MEC）也逐渐成熟。MEC将无线网络和互联网技术融合在一起，工业作为5G的一个应用方向，可以将MEC 应用于现场设备实时控制、远程维护及操控、工业图像处理等方面［1］。任务计算量的提升导致本地设备自身无法处理相应的计算任务，而云计算的提出则很好地解决了算力不足的问题；但是云计算也带来了数据传输成本、云存储花费、互联网访问管理和安全性等一系列问题［2］。MEC 将端云架构转变为端边云架构，在一定程度上降低了时延，并通过合理的计算卸载策略提高了计算任务的吞吐量，能更好地满足用户体验质量需求，使经济利益最大化。计算卸载作为MEC 的研究方向之一，自2014 年提出以来，工业界与学术界已经对其进行了大量的研究。目前的卸载策略控制方式主要是集中式控制与分布式协作控制，在建模场景方面主要包括单用户单MEC、多用户单MEC 和多用户多MEC，优化目标主要包括能耗约束条件下最小化时延、时延约束下最小化能耗以及平衡能耗与时延的卸载策略。目前研究的问题大部分是对于通用场景下的问题建模，针对工业场景下计算卸载策略的研究比较少。考虑工业生产线中实际的卸载条件，工业场景相较于通用场景下的计算卸载策略存在以下不同：1）工业场景下接入MEC 服务器的设备数目多，需要考虑一种总体最优的策略；2）工业场景下对于时延特性的要求会更加严格，主要关注如何最小化时延；3）工业场景下MEC 服务器会处理大量特定（图像识别、设备控制等）的任务，需要选择合适的计算模型以及通信方式。

本文主要考虑了工业生产线中的计算卸载策略，在多用户多MEC 场景下，研究在能耗约束条件下时延最小化的问题，通过集中控制卸载高计算量的任务到MEC 服务器。工业生产线中可以降低传输能耗与计算能耗，选择合适的通信方式以及数据压缩来降低传输能耗［3］；通过提高MEC 服务器的处理性能来降低计算能耗。当前卸载策略应用场景是通过虚拟现实（Virtual Reality，VR）眼镜来实时识别和控制工业生产线中的设备，对于时延要求较高，因此选择最小化时延的卸载策略。具体的工作如下：

1）为工业场景构造时延模型与能耗模型，在MEC 系统中将计算卸载问题转化为时延最小化时延模型，其中能耗模型作为约束条件；

2）提出通过智能优化算法中的粒子群优化（Particle Swarm Optimization，PSO）算法来解决最小化问题，对于离散粒子群算法进行了一定修改来适应问题；

3）通过仿真实验表明完全本地卸载策略与MEC 基准卸载策略都存在各自的优缺点，而本文提出的基于PSO 算法的计算卸载策略PSAO 能够在能耗与时延上达到相对平衡，基于人工鱼群算法（Artificial Fish Swarm Algorithm，AFSA）的卸载方案前期优化效果与PSAO 相差不大，但当设备数过多或者任务量过大时，鱼群卸载策略远不如PSAO卸载策略。

1 相关工作

欧洲电信标准协会（European Telecommunications Standards Institute，ETSI）提出了移动边缘计算（MEC）的概念，该概念将边缘计算集成到移动网络架构中［4］。2016年在原有的网络基础上接入了Wi-Fi，将MEC 的中文解释修改为“多接入边缘计算”。计算卸载是MEC中重要的研究方向，主要包含卸载决策和资源分配，本文主要关注计算卸载决策，也就是研究用户中要不要卸载、卸载什么和卸载到哪里的问题［5］。文献［6］中提出了动态卸载方案，将卸载任务看作是两级随机优化问题，通过任务排队模型，由移动设备来决定任务在本地执行还是在MEC 服务器上执行，采用马尔可夫决策过程来处理该问题，提出一种有效的一位搜索算法来解决功率受限的时延问题。文献［7］中以时延为优化目标，在文献［6］的基础上提出了自带能量收集的MEC系统，选择在线计算卸载策略，卸载过程中考虑了数据在信道中传递与CPU 上计算的各个因素，使用Lyapunov 优化来得到最优解。文献［6-7］虽然对于单个任务卸载到MEC 问题给出了解决方案，但是在工业生产线中往往有成百上千个移动设备和传感器需卸载任务，此时需要分布式的策略来进行卸载。文献［8］中从另一方面来考虑卸载任务，主要是针对一系列具有顺序关系的任务，通过拓扑图的优化方式来卸载，使用负载平衡试探法将任务卸载到MEC中，最大限度提高移动设备与云之间的并行性。其他研究中也提出了通过匈牙利算法来解决一些非顺序的任务，一般是需要本地设备进行初步处理，MEC 完成后续高计算量的任务［9］，在移动设备与云之间的并行方面也提供了新的思路。文献［10-11］中将多用户多MEC 场景建模为时延约束条件下的能量优化问题，通过AFSA来求解决策向量。文献［12］中基于云计算提出了一种快速混合多站点计算卸载解决方案，可根据移动应用程序的大小实现最佳和接近最优的卸载分区，当规模扩大时提出使用粒子群优化（PSO）的优化版本来获得非常合适的卸载优化解决方案。文献［13］中结合人工智能技术，基于长短期记忆（Long Short-Term Memory，LSTM）网络预测计算任务，提出基于任务预测的移动设备计算卸载策略。目前各个技术趋向于相互融合来达到更优的结果，通过神经网络或者机器学习来辅助优化边缘计算卸载模型。文献［14］中对近几年关于计算卸载策略的研究做了汇总，主要根据计算卸载的卸载类型、优化目标提出解决方案、场景、评估方式进行分类总结。MEC未来可能的应用方向主要集中在动态内容优化、物联网、移动大数据分析和智能交通［15］。

结合以上的研究不难发现，虽然上述研究提出的系统或者算法在能耗和时延优化方面都有着较优的性能，但是都很难符合工业生产线场景下的计算卸载低时延目标，其中文献［12］中提出的快速混合多站点计算卸载能够适应工业场景，但是由于云计算带来的成本问题以及传输时延增高等一系列问题，需要提出一种符合多用户多MEC场景下，在能耗约束的条件下时延最小化的完全卸载策略。

2 系统模型

MEC 系统的部署场景如图1 所示，MEC 服务器主要面向时延敏感型和计算量巨大的任务，核心任务包含工业设备的控制与工业设备的识别。本地设备（移动设备、传感器等）主要执行数据收集或者是前期数据处理，在脱离MEC 服务器的情况下只能进行简单任务的处理，需要将计算任务传输到对应的MEC 服务器进行计算。MEC 服务器部署的位置比较灵活，本文选择将MEC 计算服务器部署于微蜂窝基站上，在微蜂窝基站上实现具体的计算功能，本地设备通过无线的方式与服务器之间进行交互。针对工业生产线中的计算卸载问题：首先，在工业生产线中将会接入各种类型的移动设备（全景摄像头、智能手机、AR 眼镜等），移动设备也具有一定的计算能力，即“多用户”；其次，在工业生产线中往往需要多个MEC 服务器来处理任务，即“多MEC”。PSAO 卸载策略应用于AR眼镜与工业设备的实时交互，需要保证低延迟。

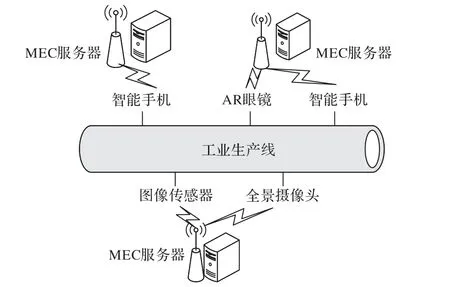
图1 多设备多MEC系统模型Fig. 1 Model of multi-device multi-MEC system

假定在当前网络中包括K个移动设备，N个MEC 服务器。每一个移动设备产生任务后指定一个服务器（或本地）来执行，最后找到所有任务最优的执行位置，即计算卸载向量V，卸载结果会有N+ 1 种可能性，任务可能会在本地执行或者将任务装载到N个MEC 服务器中的其中一个，并由装载服务器执行。

2.1 时延模型

根据任务在不同设备上运行，时延模型也会存在差别：如果当前任务在本地设备执行并且每个任务都没有排队延迟，此时只需要考虑本地计算时延；若将任务卸载到MEC 服务器执行，完成当前任务所需要的时延主要包括传输时延、MEC计算时延、反馈时延，其中反馈时延远远小于传输时延，因此在本文中将忽略反馈时延。表1 详细介绍了系统建模中使用的符号含义和在仿真实验中的取值，其中：下标i表示当前当前移动设备编号，j表示当前MEC 服务器编号，u 表示移动设备标识，s表示服务器标识。

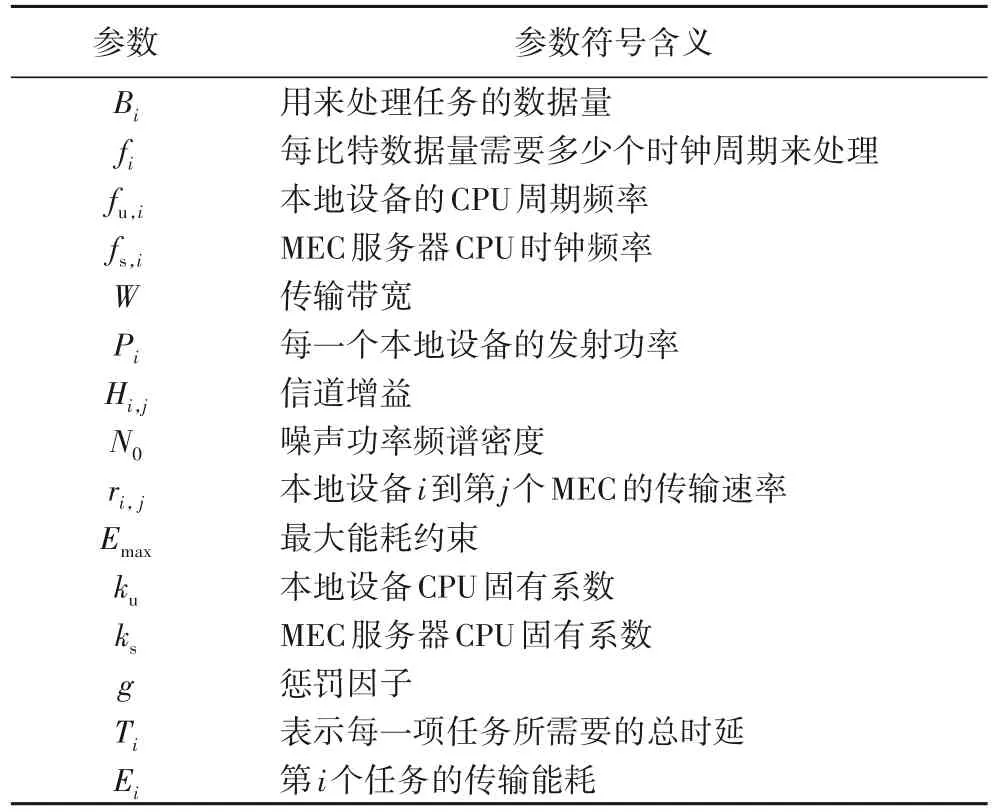
表1 系统建模中使用的符号含义Tab. 1 Meaning of symbols used in system modeling

1）本地计算时延。

式（1）表示本地计算时延与本地CPU 周期频率的倒数成正比，Bi*fi表示当前任务计算量。

2）MEC传输时延。

在考虑计算MEC 计算时延之前，需要去定义通道传输速率，根据香农定义可知：

已知当前任务在通道中的传输速率为式（2），当前任务计算量为Bi*fi，则传输时延为：

3）MEC计算时延。

式（4）表示MEC计算时延与MEC服务器周期频率的倒数成正比。

2.2 能耗模型

1）计算能耗。

CPU 的算力与芯片架构有着密切的关系，每一代CPU 架构都有固定的能耗比，在同架构前提下，功耗与电压和频率都成正比［16］，设备之间的能耗也会受到计算任务量的影响：

其中：电容Ci取决于有效开关电容；L表示电压。

2）传输能耗。

传输能耗针对的是卸载到MEC 服务器上的任务，在时延模型中已经计算出传输时延，则传输能耗为：

2.3 计算模型

2.1 节和2.2 节对工业生产线问题抽象建模：首先当前MEC 的垂直应用场景主要是针对计算密集型和延迟敏感型计算任务，其中包含工业中的增强现实图像识别；其次需要确保每一项本地设备的平均能耗都小于最大能耗，因此实际建模为在能耗约束条件下的最小化时延问题。

完成一个卸载任务的总时延为传输时延与服务器计算时延的和：

本地执行一个任务的总时延为：

由式（7）与式（8），可以得到针对某一个计算任务，在本地设备计算与MEC 服务器计算时会有不同的时延求解公式，可以将当前问题联合表达为：

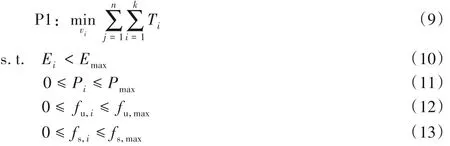
其中：式（9）表示找到使得满足时延最小的卸载决策向量，vi表示任务i具体分配到的服务器编号；式（10）表示能耗约束，每个任务所耗费的平均能耗小于最大能耗；式（11）表示本地设备的CPU 周期频率小于最大CPU 周期频率；式（12）表示MEC 服务器的CPU 周期频率小于最大CPU 周期频率。P1 更加关注在整个卸载过程中的时延问题。

再考虑这样一种情况：其中一个MEC 服务器性能更优，按照式（9）的建模方式，因为没有考虑到排队时延，导致大多数任务会卸载到性能更优的MEC服务器，性能优秀的MEC服务器的平均功耗会高于最大能耗，如果能将当前任务卸载到其他MEC 服务器则可以缓解负载压力。因此选择将P1 问题转化为增加惩罚函数的P2问题：当设备平均能耗大于最大能耗时，通过增加惩罚函数的形式，来使得任务卸载到当前MEC服务器的系统总成本增高。

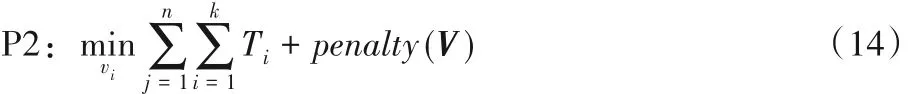
其中：

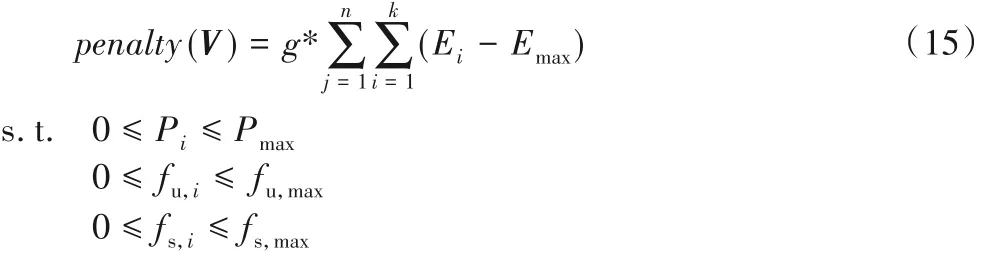
其中：V表示需要求解的卸载向量；g表示惩罚系数，随着计算消耗的能耗越多，则惩罚项越大，如果不超过最大能耗则不惩罚，增加惩罚函数的意义在于平衡能耗与时延。P2 更加关注在整个卸载过程中的时延与能耗的平衡。

3 基于PSO算法的优化

PSO 算法受鸟类捕食行为的启发并对这种行为进行模仿，将优化问题的搜索空间类比为鸟类的飞行空间，将每一只鸟抽象为一个粒子，粒子无质量无体积，用以表征问题的一个可行解，优化问题所要搜索到的最优解等同于鸟类寻找的食物源［17］。

3.1 粒子编码

假设粒子群规模为U，K 表示当前本地任务数量，N 表示MEC 服务器的数量，所有任务的集合可以表示为M={m1，m2，…，mk}。首先对任务进行定量描述，假设编号为i的移动设备产生 mi(Bi，fi，Emax)个任务待计算。其中：Bi表示输入数据量，fi表示计算密度，Emax表示任务的能耗约束。所有MEC 服务器周期频率集合S = {s1，s2，…，sn}，包含了当前系统中所有服务器的CPU 周期频率。信道增益矩阵H =用来计算任务传输到MEC 服务器的最大传输速率，Hi，i的信道增益为0，Hi，j（1 ≤i ≤K，1 ≤j ≤N，i ≠j）表示移动设备i 产生的任务传输到编号j 服务器所需要的信道增益。

粒子个体采用整数编码，每一个粒子的元素可以取1到N之间的任意整数，粒子编码的维度与任务集合的个数相同。假定当前任务集合包含 5 个任务 M={m1，m2，m3，m4，m5}，粒子编码为[0，1，2，5，1，2]表示所有任务的执行位置，其中第一个元素0 表示m1任务直接在本地进行计算，第二个元素1表示m2任务将要装载到编号为1 的MEC 服务器执行，以此类推。

粒子表示当前所有任务将要卸载到的具体某个MEC 服务器。每一个粒子的卸载决策向量V ={v1，v2，…，vk}表示所有任务最优的执行位置，其中vi在0到N中随机取值：vi= 0表示当前任务直接在本地执行；vi= j(1 ≤j ≤N)表示当前任务装载到第j个MEC服务器，并由第j个服务器执行。

粒子的速度表示当前任务分配到其他MEC 服务器的趋势快慢，记作Xi={x1，x2，…，xk}，粒子速度随机初始化为整数值并在更新过程中进行取整，粒子速度的编码维度与任务集合的数目相同。假定当前任务集合包含5 个任务M ={m1，m2，m3，m4，m5}，粒子速度为[0，3，1，4，1，2]，其中第一个元素0表示m1任务依旧由原来的MEC 服务器处理，第二个元素3 表示m2任务由原来下移3 位的MEC 服务器处理，以此类推。

每一个粒子在所有迭代过程中的最优位置记作Pbest={ p1，p2，…，pn}，表示当前粒子找到的使得系统总代价最小的任务分配方式；记录所有粒子中出现的最优位置，记作Gbest={g1，g2，…，gn} ，表示所有粒子中系统代价最小的分配方式。

3.2 适应度函数

粒子的适应度表示所有任务分配到不同MEC 服务器的系统总代价，计算公式为：

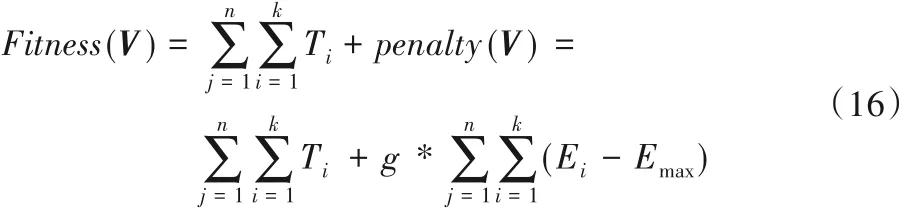
3.3 计算卸载流程

粒子群速度更新的决定因素主要包含三部分：第一部分主要是自身原来的速度，也可以称作“惯性影响”；第二部分主要是自身记忆的最优位置，也可以称作“认知影响”；第三部分主要是全部粒子记忆的最优位置，也可以称作“社会影响”。最后用粒子群算法解决计算卸载问题。

算法1 基于PSO算法的卸载流程。

输入：

1）本地任务集合M = {m1，m2，…，mk}，MEC 服务器集合S ={s1，s2，…，sn}，信道增益矩阵H。

2）算法控制参数：粒子群规模N = 25，迭代代数maxGen = 100，速度边界 vmax为 MEC 服务器个数的 2 倍，位置边界 pmax为 MEC 服务器的个数，学习因子 c1= 1.5，c2= 1.5 惯性因子Wp= 0.4，惩罚因子g = 1 × 10-2.5。

输出：

最 优 分 配 向 量 Vi={v1，v2，…，vn} 与 最 小 延 迟Fitness(V)。

初始化：

1）初始化每一个粒子的随机位置Vi与速度Xi，其中i 表示第i个粒子。

2）初始化适应度值：通过本机任务集合M、MEC服务期集合S 和信道增益矩阵H 计算时延与能耗，按式（16）来计算每一个粒子的适应度。

3）初始化粒子最优分配与全局最优分配：将粒子当前位置设置为个体最优任务分配方案Pbest，并将适应度值最小的粒子的位置设置为群体最优分配方案Gbest。

迭代计算：

4）令迭代次数t = 0

5）while t ≤ maxGen

a）更新速度。粒子中的每一个维度独立去更新速度X[i]，如果速度大于vmax，则令X[i]= vmax。粒子速度的更新公式为：

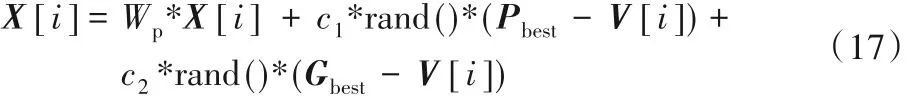
其中：c1和 c2为学习因子；Wp为惯性权重：rand（）为 0～1的随机数。

b）更新位置。粒子中的每一个维度独立去更新位置V[i]，如果 V[i]位置大于 pmax，则令 V[i]= pmax。粒子位置的更新公式为：

c）更新粒子最优分配与全局最优分配。通过本机任务集合M、MEC 服务期集合S 和信道增益矩阵H 计算时延与能耗，按式（16）来计算每一个粒子的适应度。如果更新后的适应值小于当前适应值，则更新粒子最优分配方案Pbest、群体最优分配方案Gbest和系统总代价Fitness(V)。

d）t = t + 1

6）End

输出结果：

7）得到最佳分配向量V[i]= Gbest和最小延迟Fitness(V)。

8）如果最优解不满足，则转到步骤1）；否则输出最优分配向量Vi={v1，v2，…，vn}与最小延迟Fitness(V)。

最后通过集中控制的方式，vi(i = 1，2，…，K) = 0 将该任务放入本地设备中执行，vi=j(j= 1，2，…，n)将该任务放入对应编号j的MEC服务器中执行。

4 仿真与结果分析

4.1 仿真环境以及参数设置

通过Java 语言实现了PSO 算法，从而具体地评估所提出的计算卸载策略的性能。在工业生产线场景中，设备的个数K=［50，100，150，200，250］，MEC 服务器的个数为10，分别有K个移动设备向10个服务器发起卸载请求。仿真用到的主要参数取值与符号含义［10］如表2所示。

4.2 结果分析

根据表2 的参数取值进行仿真实验，本文选择四种卸载策略进行对比：本地卸载策略、MEC 基准卸载策略、基于人工鱼群算法（AFSA）的卸载策略和PSAO；同时也通过PSO 算法优化基准卸载策略在卸载过程中的平均总时延。在实际生产环境中本地设备只能进行简单任务的处理，仿真实验中假设本地设备也能够处理高计算量的任务，假设每一项任务到达即执行，不会存在任务排队导致的时延增加。

表2 主要参数取值与符号含义Tab. 2 Main parameter values and symbol meanings

图2 为不同能耗约束下不同卸载策略的系统总代价对比，设置设备数K= 50，MEC 服务器的个数N= 10，每一项任务数据量大小Bi= 3 Mb。可以观察到，随着能耗约束的增大，四种卸载策略系统总代价降低。当能耗（单位：J）约束为0时，本地卸载策略的系统总代价远远高于其他三种卸载策略，这是由于本地设备处理任务将会产生较高的能耗；能耗约束为750 J 时，本地卸载策略代价开始低于MEC 基准卸载策略，这是由于能耗约束的增大，模型对能耗约束的敏感度降低，因此需要选择合适的能耗约束。PSAO 卸载策略在不同的能耗约束下都优于其他MEC 基准卸载策略和本地卸载策略，当能耗约束大于750 J 时，基于AFSA 的卸载策略与PSAO 卸载策略优化效果相差不大。

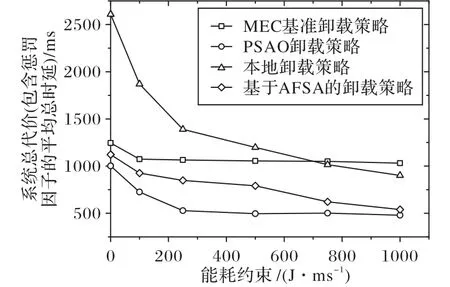
图2 能耗vs. 系统总代价Fig. 2 Energy consumption vs. total system cost

图3 对PSAO 卸载策略的收敛性进行评估，设置设备数K= 50，MEC 服务器的个数N=10，每一项任务数据量大小Bi=3 Mb，通过改变迭代次数来观察所有任务的平均总时延。

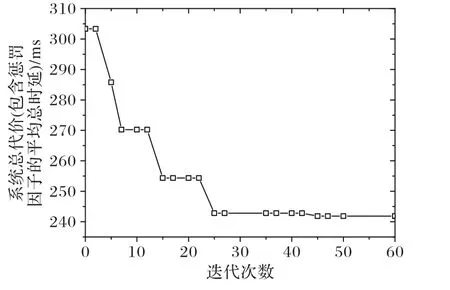
图3 收敛性分析Fig.3 Convergence analysis

由图3可以观察到，算法在前25次迭代过程中收敛较快，迭代50 次后系统总代价保持不变，找到全局最优解。PSAO具有很强的全局优化能力，在算法的前期不断寻找全局的最优解，且在后期具有良好的全局搜索能力。PSO 算法优化后平均总时延从原来的303.33 ms 降低至241.824 ms，并在后期迭代过程中保持不变，相比原来系统的总时延降低了20%。

图4 为不同设备个数的情况下，不同卸载策略的系统总代价对比。MEC 服务器的个数N= 10，每一项任务数据量大小Bi= 3 Mb。可以观察到在设备数分别为50，100，150，200，250 时，平均总时延是处于增长的趋势，这是由于随着设备数的增加，所需要的处理时间与传输时间也随之增加；但是，随着任务数目的增加，PSAO卸载策略总时延增长幅度远远小于MEC 基准卸载策略与本地卸载策略。基于AFSA 的卸载策略在设备数小于200 时，优化程度与PSAO 卸载策略相差不大；但当设备数目大于200 时，系统总代价开始急速上升，远远高于PSAO卸载策略。

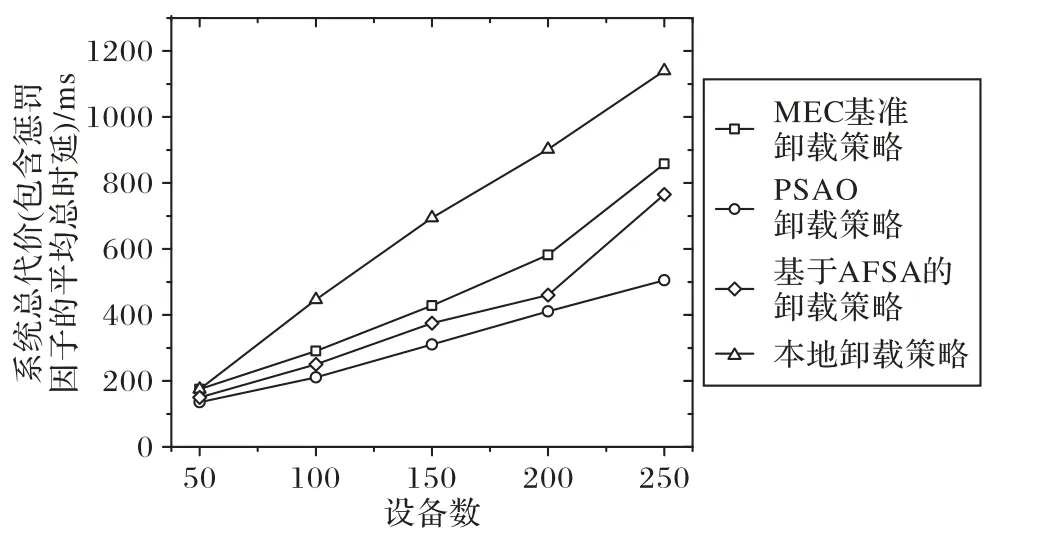
图4 设备数vs. 系统总代价Fig. 4 Number of devices vs. total system cost

图5 为不同任务量的情况下，不同卸载策略的平均总时延对比。设置任务数K= 50，MEC 服务器的个数N= 10，可以观察到：在任务量分别为3、10、15、25、40 Mb 时，随着任务量的增加，平均总时延也逐渐增加。本地卸载策略比其他策略增长速度更快，表明随着任务量的增加会导致更多的时间与能量消耗。其中，基于AFSA 的卸载策略在任务量小于15 Mb 时，与PSAO 卸载策略优化效果相差不大；但是在任务量大于15 Mb 时，容易收敛于局部最优，并且在后期搜索过程中盲目性比较大，卸载效果不理想。PSAO卸载策略增幅程度远远小于MEC 基准卸载策略与本地卸载策略，并且在任务量过大时可以取得最佳效果。

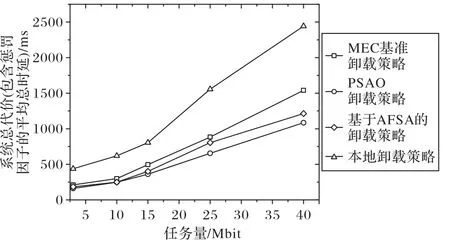
图5 任务量vs. 系统总代价Fig. 5 Task size vs. total system cost

5 结语

本文将工业生产线中的计算卸载问题建模为多用户多MEC 时延优化问题，为了消除本地设备使用能耗来换取时延的问题，通过惩罚函数平衡时延与能耗，并提出基于PSO算法优化的卸载策略PSAO。基于分析结果可知，本地卸载策略与MEC 基准卸载策略都有一定的局限性，本文选择PSAO 卸载策略让本地设备和MEC 服务器协作计算，使原本系统总代价降低了20%，并且随着设备数目和任务量的增加，它的增幅程度远小于本地卸载策略和MEC 基准卸载策略，满足延迟敏感型应用的服务质量要求；基于AFSA 的卸载策略虽然能够起到一定的优化作用，但在设备数增加和任务量增大的情况下，无法找到任务最佳分配方案。工业系统对于可靠性要求非常高，PSAO 卸载策略属于启发式卸载策略，大部分启发式算法能够生成高质量的近似最优解，由于启发式方法的结果是随机产生的近似解，因此缺少可靠性［18］。未来将会考虑粒子群与其他优化算法相结合，提高寻找到最优解的鲁棒性，从而在降低时延的前提下，提高整个卸载策略的可靠性。