双排不等距圆截面桩板墙的简化计算与设计应用
2020-09-03谢瑾荣刘可
谢瑾荣,刘可
(1.中交第四航务工程勘察设计院有限公司, 广东 广州 510230; 2.中交城市投资(宁波)有限公司)
门架式桩板墙是一种直立式边坡支护结构,在变形控制要求高且无法设置内外支撑的条件下应用较多,该结构整体截面惯性距较大,抗弯能力强,支护效果好。为便于计算,门架式桩板墙的前后桩常采用等间距形式布置,如矩形或梅花形。而为了最大限度减少工程量,节约工程造价,前排桩和后排桩各自的水平间距应可以不相等设置,如前后排桩采用T字形布置,但是,T字形布置的双排桩门架式结构的空间体系受力计算则较为复杂。钱同辉等将双排门架式抗滑桩视为单层多跨框架结构,提出了桩梁土空间协同作用下的双排门架式抗滑桩受力空间模型,计算较为繁琐;李宝田等通过有限元法计算得到了排架桩的位移、弯矩、剪力等力学指标;赵波等采用有限差分软件对双排桩的桩土空间效应进行了模拟。上述数值分析法建模工作量大,耗时较长,且不易求解。而工程人员在设计中需要一种既安全又高效的计算方法。
该文以广东省湛江市某路堑边坡支护工程为例,针对双排不等距桩板墙结构提出简化分析计算法。
1 双排不等距桩板墙受力机制分析
双排不等距圆截面桩板墙是由前排支护桩、后排锚固桩、前排桩顶冠梁、前后桩系梁以及挡土板组成。前桩通过冠梁连接形成整体支护能力,后桩通过系梁与前桩冠梁连接,整体呈T字形分布,是具有整体抗弯能力的空间超静定结构(图1)。

图1 双排不等距圆截面桩板墙
对土压力作用下该结构的受力机制进行分析:
(1)该结构前后排桩呈T字形分布,后桩与其相邻的前桩及其连接的系梁构成了平面刚架结构。
(2)相邻刚架之间为1个受荷单元,滑动面范围内土压力荷载作用在前排桩和挡土板上,挡土板又将荷载传递至相邻前排桩,前排桩凭借抗弯能力、嵌固作用、支反力等抵抗单元范围内的主动土压力。
(3)在冠梁的作用下,前排桩形成了受力整体共同抵抗土压力作用,部分土压力荷载在结构发生整体变形趋势后传递至平面刚架处。
(4)平面刚架处的后桩对前桩具有“锚拉”作用,抗弯能力远大于单桩结构,对整体结构的位移变形起到控制作用,平面刚架处可视为前排桩结构的支点。
(5)平面刚架除分担部分前排桩荷载外,还需抵抗自身范围内的土压力,在该土压力作用下平面刚架结构发生位移和变形,因此,该支点实为弹性活动支点。该弹性活动支点与前排桩相互变形协调,空间内力再分配。
2 结构简化分析与计算
周翠英等将前后排桩及中间连系梁和桩间土视为整体,将前、后排桩受到的岩土体抗力简化为弹性支承,提出了桩土作用计算模型,该研究为此次简化计算提供了理论依据。该文将双排不等距桩板墙结构视为弹性支座下的桩板墙结构模型(图2),将该模型简化分解为单支点桩板结构模型与平面刚架结构模型的线性组合。

图2 双排不等距桩板墙简化分析模型
采用平面杆系结构弹性支点法分别计算得到土压力作用时单支点桩板结构响应与平面刚架结构响应,将两种响应线性叠加得到简化模型的空间位移响应(图3)。

图3 固定支座下桩板结构模型与门架结构模型
假定桩前土符合Winkler弹性地基梁理论,单支点桩板结构支点刚度为无限大。采用弹性支点法计算得桩板结构前桩水平位移V0;刚架结构根据余志成提出的双排桩计算公式,将其视为底端嵌固的平面刚架结构模型,桩身土压力分布与悬臂高度、桩排距有关,计算得前桩水平位移V1。叠加得双排不等距桩板墙结构的前桩水平位移:V=V0+V1。
3 实例应用
3.1 工程概况
实例工程位于湛江市经济技术开发区,道路按城市次干路标准建设,红线宽度28 m,其中K0+520~K0+645段左侧路堑边坡总高5~9 m,为土质边坡,坡后为山体公园,植被茂盛。距道路边线9 m处有佛塔1座,位于边坡开挖范围内。经各方磋商,该佛塔不得拆除,且山体公园内植被不得破坏,因此该路段边坡须采用直立式支护方案。
勘察资料显示,场地揭露的地层为第四系下更新统湛江组海陆交互相沉积层,自上至下分布为:黏土1:灰黄色,湿,可塑,黏性一般,层厚7.0~8.0 m;黏土2:灰色,湿,可塑,黏性较好,层厚13.5~18.0 m。其岩土参数如表1所示。
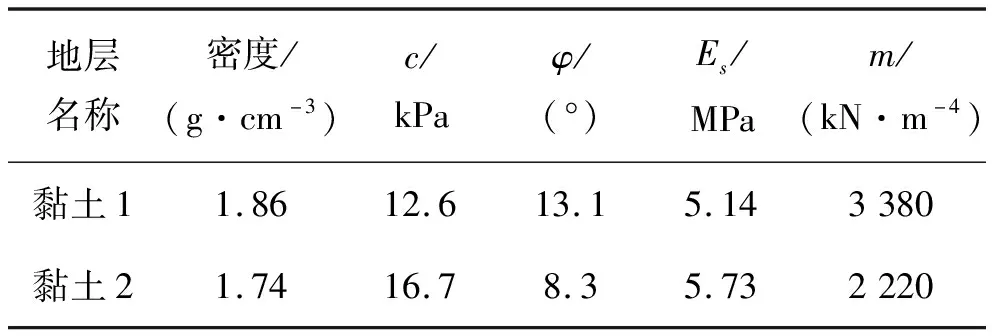
表1 地层岩土参数表
3.2 边坡支护设计
边坡支护结构设计应从经济性、安全性和适用性三方面考虑,此次拟定了矩形截面桩板墙、圆截面桩板墙+锚索支护、门架式桩板墙、双排不等距圆截面桩板墙共4个直立式支护方案,对以上方案进行综合评价分析,结果如表2所示。

表2 支护方案选型
该工程濒临海边,地下水发育,采用人工挖孔施工风险和难度偏大,施工进度不满足要求,因此支护桩采用机械成孔的圆截面钻孔灌注桩。实例边坡属于土质边坡,黏土层深厚,桩前被动区土体抗力有限,如采用单排悬臂桩板墙方案,悬臂端顶部最大水平位移计算值已达82 mm,超出规范30 mm的限值要求,须辅以锚索支撑,而锚索在该地层中其锚固体摩擦力发挥效果欠佳,且远期预应力损失较大,不适宜作为永久性边坡支护方案。若采用门架式桩板墙方案,其抗弯刚度大,支护效果明显,但前后桩等距设置工程量较大,总工期较长,经济性一般。综上分析,采用双排圆截面桩板墙且前后桩不等距设置为最合理方案。
设计方案前桩水平间距采用2.5 m,悬挑比按1∶2控制,后排桩水平间距10 m,前后桩排距5 m,同深度设置,方案平面、立面布置见图4。前桩顶部设置高1 m、宽2.5 m冠梁,系梁截面与冠梁相同,桩梁材料均采用C35 钢筋混凝土。

图4 双排不等距圆截面桩板墙方案平面、立面布置(单位:m)
3.3 计算结果分析
简化法分析采用理正岩土系列软件计算得到土压力作用时固定支座下的桩板结构位移与门架结构位移,二者相叠加得到双排不等距桩板墙的桩身位移响应。为对照分析,采用Midas GTS三维有限元软件计算得到有限元解,并选取Z31、Z33、Z35、Z37、Z39、Z41、Z43、Z45共8个支护桩作为桩身位移实际监测点。将以上观测点的桩顶水平位移计算值与实测值汇总如图5所示。

图5 桩顶水平位移计算值与实测值对比
从图5可看出:简化法计算结果与有限元法及实测数据基本符合。前桩的水平位移分布呈锯齿形,简化法计算所得桩顶最大水平位移为15.4 mm,发生在Z31桩,其桩顶实测水平位移为13.2 mm,远小于单排悬臂桩的桩顶最大水平位移82 mm,满足规范要求,后桩对前桩起到了明显的“锚拉”作用,支护结构整体具有较大的抗弯能力。
提取Z31桩身水平位移(图6)可知,桩身最大水平位移为18.8 mm,约为单排悬臂桩的最大水平位移的25%。简化法与实测值最大误差为3.2 mm,有限元法与实测值最大误差为1.7 mm,简化法、有限元法分析结果与实测值平均误差率分别为19%、11%,有限元法计算结果与实测值较为接近,这是由于有限元法对桩土体的变形协调和三维空间效应计算更加精确。然而,简化分析法无需建立复杂的三维有限元模型,计算更为快捷,误差精度满足岩土工程设计要求,且结果偏于安全。

图6 Z31桩身水平位移
4 结论
(1)该文将双排不等距桩板墙结构视为弹性支座下的桩板墙结构模型,并将结构响应简化为单支点桩板结构与平面刚架结构的响应叠加,实例应用表明简化计算思路较有限元法更安全高效。
(2)双排不等距圆截面桩板墙依靠自身结构的空间性抵抗土侧压力或滑坡推力,其桩身位移小,抵抗力大,且适用性强,安全风险小,其前后桩水平间距可灵活设置,是一种值得推广的直立式路堑边坡支护结构。
