黔江官河大桥施工监控影响因素敏感性分析研究*
2020-09-03刘清川祝朝伟
冯 晓,刘清川,祝朝伟
(1.重庆交通大学,重庆 400000;2. 重庆祝桥建筑工程有限公司,重庆 401120)
在桥梁施工过程中,有诸多的影响因素会使桥梁的线形和结构状态与设计状态产生一定的偏差[1]。当出现偏差时,如果不对施工进行调整,可能会导致施工安全事故,或者成桥后实际状态的线形、内力等与设计不符。在造成偏差的影响因素中,各影响因素的影响程度不同。因此,判断出对桥梁施工影响较大的因素很有必要,在施工控制中,对主要的影响因素进行调整,可使后续施工得到有效地调整,这对于提高施工精度、施工效率、施工控制精细化有现实意义。
1 工程概况及施工监控
1.1 工程概况
官河大桥是重庆市黔江区省道S304正阳至彭东段改建工程,起于巨木岭正阳园区路跨越阿蓬江与现有老路结合,此项目是一条一级公路,其建设将使正阳新区、正阳工业园、物流园、创业园和彭东镇紧密连接,从而极大缩短城乡距离,有助于黔江区协调均衡发展。
黔江官河大桥为主跨147.64 m的箱型拱桥,主拱采用断面形式为装配式单箱五室箱型拱,箱高2.8 m,总宽8.3 m,净跨径145 m,净矢高为35 m,净矢跨比为1:4.143,计算跨径为147.064 m,计算矢高为35.454 m,计算跨矢比为1:4.148。主拱线形为悬链线,拱轴系数为1.908。图1为官河大桥示意图。
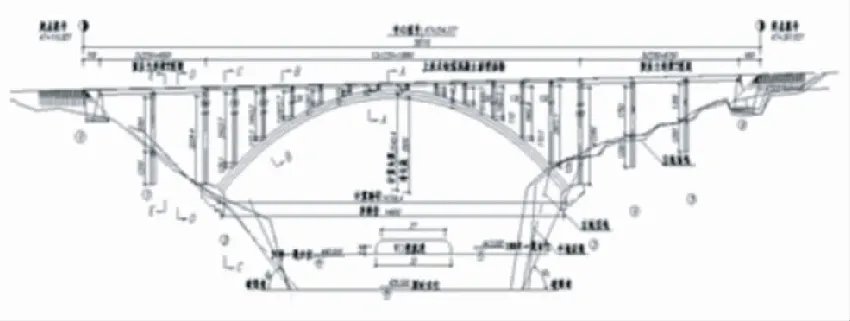
图1 官河大桥立面图
根据官河大桥的实际地形地貌,以及施工现场的场地条件,官河大桥的主拱圈施工采用缆索吊装施工法[2]进行。具体做法是先按照设计图纸对拱肋分节段预制,等预制构件达到足够强度时利用缆索吊装系统将预制拱肋提升至预定位置,再用扣索采用斜拉扣挂的方式固定,检查拱肋线形和标高,再逐次进行余下阶段施工。图2是官河大桥缆索吊装示意图。
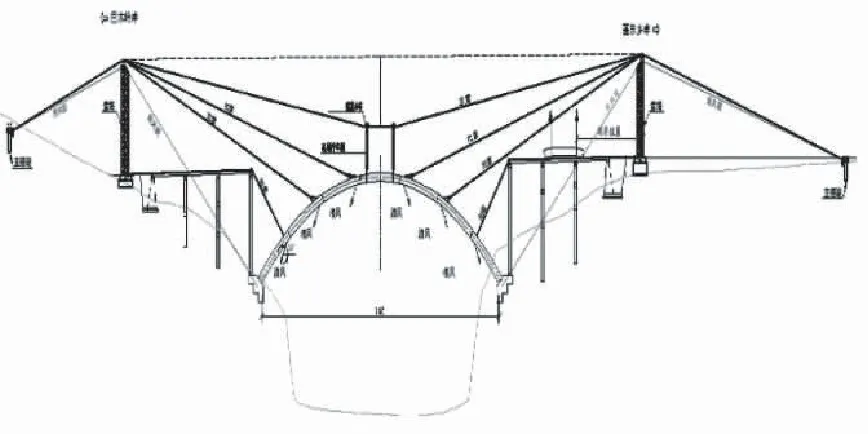
图2 官河大桥缆索吊装示意图
1.2 官河大桥施工监控
官河大桥采用缆索吊装施工,因此,施工监控的目标主要分为拱肋的线形和标高监测,缆索吊装系统的安全稳定监测。
(1)拱肋标高的控制可根据设计标高在实际的拱肋上确定出标高位置,并在相应位置上贴上反光标志,再利用现场的控制点放样的方法来调整拱肋的位置使拱肋达到预定标高。
(2)拱肋的线形控制的方法是在预制拱肋顶部中央画出标志鲜明的线,并且在引桥部分位于拱轴线的延长线上,两边分别布置经纬仪,观察所做的标志线是否位于设计轴线上,若不在设计轴线上,则通过两侧的缆风绳反复调整拱轴线,使拱肋顶部的标志线与设计轴线重合为止。
(3)塔架是保证吊装过程安全的主要承重构件,因此对塔顶的位移和塔架基础沉降的观测对保障施工安全有着重要的意义。对于塔顶的位移观测,通常是在塔顶设置几个水准标尺,然后利用全站仪分别在上下游方向以及桥轴线的方向对水平标尺进行观测,从而得到塔顶的位移值。
(4)塔架基础的沉降通常在塔架基础的上边布置多个水准点,然后利用精密水准仪测量各个水准点的高程,从而确定各个基础沉降点的高程变化值。
(5)主索垂度的观测方法是在两岸河堤上适当地方确定一控制点,测出控制点标高和距跨中距离,在控制点上置全站仪,观测主索跑车位置,读出竖直角,即可计算出垂度值。
(6)主索的索力可以用频谱分析仪测试。锚碇位移方法是在锚碇上设置若干个标志点,利用全站仪观测各测点是否发生位移。
2 施工偏差原因及其敏感性分析
2.1 引起施工偏差的原因
桥梁施工过程是一个很复杂的过程,在整个施工过程中,难免会出现施工状态值与设计状态值出现一定的偏差,引起偏差的主要原因主要分为三大类:结构参数误差、施工误差、与时间有关的误差。
结构参数误差是桥梁施工过程中的一些重要参数的实际值与设计值不严格一致所带来的偏差[3]。结构参数误差主要有结构界面尺寸偏差、材料弹性模量、材料容重、材料温度膨胀系数、施工荷载、预加应力等等。这些参数带来的偏差可能导致桥梁结构缺陷,使成桥后的线形和应力状态达不到设计的要求。
施工误差一方面由施工单位的施工水平和施工管理共同决定,一个施工水平较高并且施工管理优良的施工单位,其施工项目往往执行较好。另一方面,施工误差还与施工监控密切相关,如果施工监控出现误差,势必影响后续施工,因此施工监控误差也是成桥时结构和线形与设计不符的原因之一。施工中要利用施工监控的数据对后续施工进行理论计算,理论计算中的模型误差也是引起偏差的原因之一,因为计算模型与实际的参数不可能完全一致。
与时间相关的误差是随着时间的推移,桥梁结构受与时间有关的参数的影响,从而导致的偏差[4]。一般与时间有关的参数主要是混凝土受温度变化的影响、混凝土徐变的影响。混凝土与一般材料一样具有热胀冷缩的特性。因此冬期施工[5]和高温施工[6]混凝土热胀冷缩效应区分明显,可能会造成一定的偏差。混凝土自身的徐变[7]是在其承受荷载不变的情况下随着时间的推移而不断增长的变形。桥梁从建设到投入运行的时间一般不会很短,因此混凝土收缩徐变也是施工监控考虑的重要因素之一。
2.2 偏差原因敏感性分析
2.2.1 敏感性分析概述
敏感性分析的目的是为了确定出对结构状态影响较大的偏差原因和对结构状态影响较小的偏差原因,从而在后续的施工监控过程中对重要影响因素进行控制和调整,来达到控制施工误差的目的[8]。并且在施工过程中对影响较小的偏差原因进行适当放宽,来达到简化施工的目的。
敏感性分析方法的实质就是控制变量法[9],要分析某一参数对结构状态的影响,保持其他参数不变,将要分析的因素进行修改,在带入到理论计算模型中,计算出此因素对结构状态的影响程度。对于截面尺寸等一些可量测的参数,主要是通过现场量测和实验室量测来与理论值比较其精度误差。最后通过计算得出各个影响参数的影响程度大小,确定主要影响因素和次要影响因素。
2.2.2 偏差敏感性分析
结合黔江官河大桥的现场情况,选取拱肋吊装最大悬臂端和合龙状态来进行敏感性分析。选取的分析参数主要是拱箱自重、扣索索力、混凝土弹性模量、环境温度、环境湿度等。主要分析这些参数变化对拱肋线形和标高的影响程度。分析方法是确定其他参数不变,其中一种参数上下浮动5%、10%来最后对各个参数进行重要性的界定。确定出施工监控中的主要控制对象,为施工监控工作提供便利和参考。分析幅度变化如表1所示。

表1 参数分析幅度变化
(1)自重变化影响
根据计算结果,在其他参数固定不变的情况下,如果箱型拱肋自重修改10%,吊装施工到最大悬臂端时,拱圈线形变化值与基准值差值到41.28 mm;当中间阶段合龙后,拱顶点变化值与基准值差值达到51.37 mm;如果箱型拱肋自重变化5%,施工到最大悬臂端时,拱圈线形变化值与基准值差值为32.24 mm,中跨合龙时拱圈线形变化值与基准值差值为45.36 mm。自重变化5%、10%最大悬臂端与合龙线形变化与基准值差值对比如图3、图4所示。
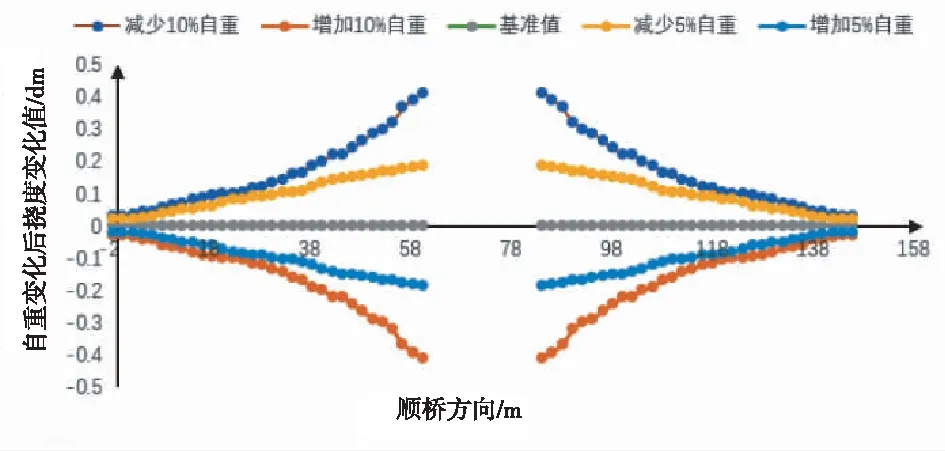
图3 最大悬臂端自重变化下线形与基准比较
由图3、图4可知,箱型拱肋的挠度值随着悬臂端的延伸而增长,合龙后线形变化值达到最大值。
(2)扣索索力影响
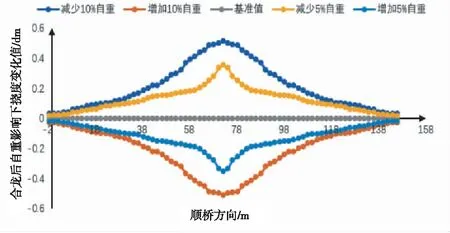
图4 合龙后自重变化下线形与基准比较
扣索是在箱型拱肋吊装到预定位置时,临时固定箱型拱肋的装置,它是调整拱肋标高和线形的主要装置。在其他参数不变的情况下,将扣索索力变化5%和10%,结果表明,扣索索力变化10%时,拱顶变化值达到12.03 cm;扣索变化5%时,拱顶变化值达到7.4 cm。扣索变化引起的线形变化值如图5所示。
由图5可知,扣索索力对线形影响值较为明显,随着吊装悬臂端的伸长,对线形的影响越大。到合龙段松开扣索之后,下沉值与理论线形值相差较大。
2.3.3 弹性模量的影响
官河大桥的主结构为混凝土箱型肋拱桥,其主要材料为钢筋混凝土(C50),混凝土的弹性模量主要是反映混凝土在受力状态下的变形情况的值,在吊装过程中,箱形拱肋主要受压应力和剪切应力作用,混凝土的弹性模量和扣索的弹性模量变化5%、10%,结果表明,混凝土弹性模量变化下悬臂端线形变化最大值为8.23 mm,在靠近拱脚处影响很小。其结果如图6所示。
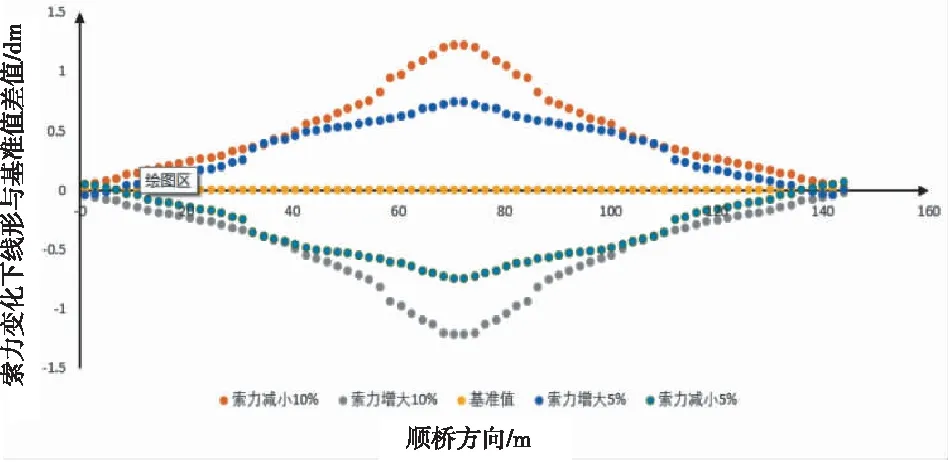
图5 扣索索力变化下线形与基准值差值
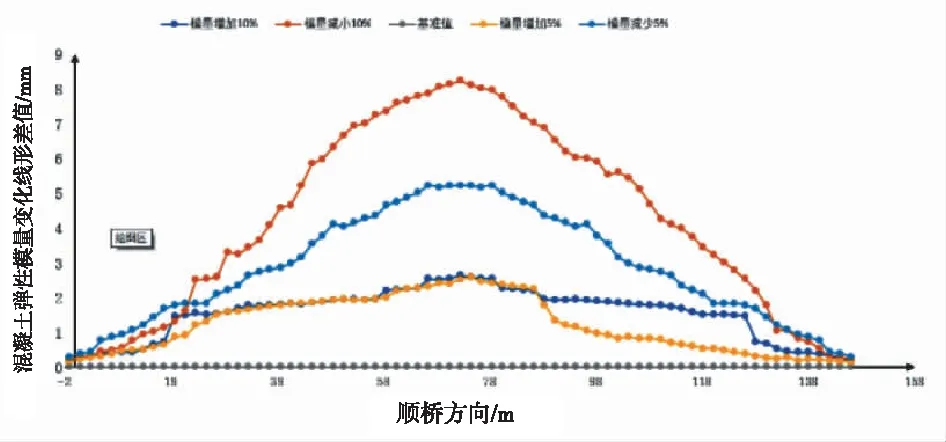
图6 混凝土弹性模量变化线形与基准值差值
由图6可知,混凝土弹性模量的变化对线形的影响随着悬臂端的伸长而增大,但是对线形影响程度与混凝土自重和扣索索力影响相比较小。
2.3.4 与时间有关参数的影响
桥梁建设的周期一般来说都是以年为单位的,建设周期较长,因此混凝土随时间推移的收缩徐变也会一定程度影响成桥的状态。影响混凝土收缩徐变的主要因素是温度和相对湿度,温度主要是影响混凝土的收缩,根据计算分析,结果表明温度上升和下降25 ℃时,对最大悬臂端的影响值最大,中跨合龙后,影响明显减小,其结果如图7所示。湿度是影响混凝土徐变效应因素之一,根据重庆市气象局数据,黔江区平均相对湿度为77%[5],湿度较大,因此分析成桥后一段时期的徐变影响对成桥线形的影响对桥梁施工有一定的指导作用,分析了成桥十年后的线形,并与基准值对比,结果如图8所示。
3 结 论
根据敏感性分析结果,在利用缆索吊装施工方法施工的箱型肋拱桥过程中,对施工影响较大的因素主要是混凝土自重和扣索索力。当混凝土自重变化5%时,线形差值达到32.24 mm,当混凝土自重变化10%时,线形差值达到41.28 mm。当扣索索力变化5%时,线形差值达到7.4 cm,当变化10%时,线形差值达到12.03 cm,对线形存在严重影响。混凝土弹性模量和温度湿度影响较混凝土自重和扣索索力的影响相对较小,混凝土弹性模量变化影响只有几个毫米,湿度变化引起的混凝土徐变十年仅2.3 cm。故在缆索吊装施工的混凝土箱型肋拱桥施工中最主要的影响因素为扣索索力和混凝土自重,次要因素为混凝土弹性模量、温度和湿度影响。在施工监控工作中应该注重拱肋预制的放样精度,以严格控制混凝土自重。在吊装施工过程中对扣索索力进行精确监控,有利于成桥线形与设计基准吻合。
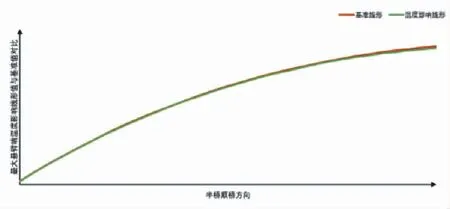
图7 温度影响线形半桥与基准差值
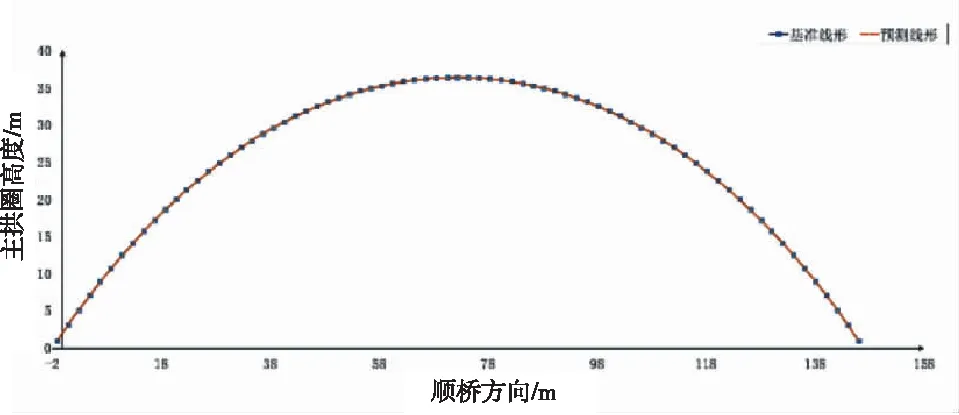
图8 湿度变化十年线形与基准线形对比
