移动群智感知多任务参与者优选方法研究
2020-09-03牛宏英刘文菊孙士民
牛宏英,刘文菊,王 赜,孙士民
(天津工业大学 计算机科学与技术学院,天津 300000)E-mail:2550633673@qq.com
1 引 言
物联网技术的出现,使得物理世界与虚拟信息世界有机结合.它成为物理世界、虚拟信息世界连接的纽带,其中感知网络成为物联网的核心.而群智感知是一种利用可移动电子终端产品来收集数据、可以取缔传统的利用专业传感器收集数据的一种新兴模式.也就是说,群智感知的便利之处在于其收集数据之前无需刻意的安装固定的传感器网络模块,这样便可以大大的减少了平台为收集数据所花费的资源成本.这里把基本感知节点设置为拥有移动终端设备的目标人群,而感知单元即为设备中所配置的各种传感器,目标人群便可将自己的设备置于附近的环境中进行数据的收集与上传.在这样的环境中,不仅数据收集者可以通过收集数据谋取所需,还可以帮助公众收集数据、分析数据、共享信息,实现互惠互利.群智感知网络利用普通用户现有的感知设备和已有的通讯网络来构建一种新兴的网络.这种利用以人为中心利用移动终端来收集数据的方式与参与者感知[2]、城市感知[3,4]、移动感知[5,6]以及众包[8]等与群智感知侧重点不太相同的系统的概念非常相似.
群智感知系统的目的是收集有效的高质量数据[1].现有的移动群智感知平台如Medusa[7],主要用于任务发布和数据收集,可以发布不同的任务与不同数据收集的处理.由平台中的参与者根据不同回报以及任务困难度[13,14]等自己决定完成某些任务.没有考虑到优化目标(比如最小化用户信息的情况下最小化移动距离).参与者选择是群智感知一个重要的研究问题之一[10,11],文献[9]中提出利用参与者已知的地理位置,使目标人群均匀分布在整个感知区域中,以达到数据收集更加完整的效果.文献[12]提出了基于社区的任务分发算法,将用户划分为不同的社区.文献[15]提出用冈珀茨函数来更新参与者的信誉度,以此实现衡量参与者参与感知任务的意愿和提供的数据质量.文献[21]提出一种多任务参与者选择方法,假设参与者信息不相同的情况下提供相同的数据质量,考虑被选择参与者提供数据的总质量以及分布情况.文献[23]部署了一个名叫‘CSP’的平台,通过WiFi热点的指纹结合其他信息推断出参与者所在位置,进而分配对应位置的任务.由于参与者的设备不同、移动速度以及隐形位置等的限制,导致其收集到的数据质量大不相同.所以平台需要在预算限制下进行参与者的选择,并激励参与者收集到高质量数据是一个重要的研究问题.
文献[20]提出一种基于组的参与者选择方法.任务分配分为在线场景和离线场景两种.离线场景下参与者选择是以物理空间位置为依据,文献[17]提出使组织者能够根据地理和时间的可用性,以及确定适合收集数据的参与者.文献[18,19]提出人群的活动行为在空间领域是有规律的,这一理论为预测参与者的运动轨迹提供了根据.文献[16]提出在多任务参与者优选的背景下实现参与者人数以及参与者移动距离的最小化研究方法,但是没有考虑到参与者速度对算法的影响.文献[21]提出了一种基于优选速度和方向的用户移动模型.这使得使用者的动作具有目的性和随机性.针对参与者选择问题,本文提出了VT-MOST一个以任务为中心的参与者选择和VPT-MOST一个以参与者为中心的优选方法.不同于T-MOST和PT-MOST中假设各参与者速度相同(70m/min),这里VT-MOST和VPT-MOST使用以往参与者的速度平均值作为参考值.一方面,对于平台而言,最小化参与者信息管理的同时最小化平台成本.另一方面,对于系统选中的参与者而言,可以实现参与者奖励的最大化.在此基础上,采用数据集对四种算法进行实验,对比并分析了四种算法所选择出的参与者人数、平均每个人完成的任务数、完成任务所移动的距离以及参与者人数与移动距离的乘积等实验结果的对比,根据不同的情况选择出性能最好的算法.
2 参与者优选模型
2.1 相关工作
群智感知激励模型即通过鼓励参与者使其积极的参与到数据收集的任务中来,以此确保服务器平台可以收集到高数量、高质量的数据,提高其系统的准确性、可靠性.文献[14]提出了边界效用密度,当参与者的边界效用密度大于密度阈值,参与者将会被感知平台选中.文献[13]中,感知平台利用参与者信誉度值选择参与者,而参与者根据完成任务的难易程度、利润值决定执行哪项任务.上述方法都没有考虑到平台信息管理资源最大化.文献[16]中,平台通过比较参与者所完成的任务个数选择参与者,既最小化用户资源管理又最小化移动距离.群智感知模型面向各式各样的生活场景,针对不同的场景提供不一样的激励机制.文献[16]提出的MultiTasker方法中,激励机制包括两部分:一部分是完成任务的奖励激励,与其完成任务个数成正比;另一部分是动态激励,根据参与者移动的总距离而动态变化,与其成正比.
本文提出的VT-MOST、VPT-MOST算法中各用户的速度不一样,由此在一定时间限制内所完成的任务个数也不一定,所以相对于T-MOST和PT-MOST,奖励激励就会有所变化.速度大的用户在一定时间限制内(比如1小时)完成的任务个数多,总距离也大,随之奖励激励、动态激励也会较大.
2.2 总体架构
移动群智感知系统由三部分构成:任务发布、任务分配和数据收集.在云端的服务器接收到数据使用者的信息请求时发送感知任务给任务参与者,处理收集的感知任务并进行其他的管理任务.参与者接收到感知任务后,进行所需数据的感知,然后将数据返回给服务器,服务器将数据处理后返回给数据使用者,通过整个流程实现数据感知、数据收集、信息服务等功能.任务分配与任务执行需要考虑多种因素[22],参与者针对不同任务的意愿程度以及收集数据对于参与者正常活动的影响都不尽相同,不同参与者由于硬件设备以及自身专业性导致收集数据的可靠性也不相同……等因素造成平台收集数据的不可控性.在感知系统中,参与者时常利用空间隐形来模糊他们的位置,实现位置隐私保护,这种方法已广泛应用于基于位置的服务[23].文献[23]设计了一种新的两阶段优化方法,包括使用隐形位置进行全局优化,然后在不侵犯隐私的情况下使用参与者的精确位置进行局部优化.这种使用隐形位置实现高传感覆盖率的方法,大大减小了平台的支出.
在任务分配时,平台通过获取用户与任务的位置,进而根据算法设计选择出合适的参与者,最后将任务分配给具体的参与者[16].在该感知系统中,参与者并不是主动选择任务而是被动的执行已分配的任务,按照既定路线来完成任务.参与者接收到感知平台的任务发布后使用自己的移动设备完成数据的采集和上传.由于平台发布的任务是紧急任务,那么参与者就要在一定时间范围内完成选定的任务集合,这就要求参与者必须有意识的去访问每一个任务点.由于任务的性质不同,可能需要参与者按照不同的形式去完成任务,同时平台为了得到高质量的数据,一个任务会进行多人多个数据的采取.参与者完成任务集合后,进行简单的计算与处理,最后统一将收集到的数据上传给系统.
3 算法设计
假设平台有任务T={t1,t2,t3,…,tn},为了保证收集的数据具有高效性与全面性,且考虑到实际情形,任务请求者要求的数据量不会不约而同的相等.所以这里假设任务请求者要求任务ti由si(si为3-8个不等)个人来完成.为了便于分析,假设参与者采集一个数据的时间为5分钟.平台中有m个候选参与者U={u1,u2,u3,…,um},则要求从m个候选者中选择若干个参与者在h小时内完成所有任务.n个任务的参与者集合表示为P={P1,P2,P3,…,Px}.x表示最终选择出的参与者人数.TUj={ti1,ti2,…}是指参与者uj完成的任务集合,UTi={ui1,ui2,ui3,…}指完成任务ti的参与者集合.完成这些任务所移动的总距离为D(TUj).在约束条件式(1)、式(2)下实现目标函数式(3)、式(4).
|UTi|=Si,i∈(1,n)
(1)
(2)
(3)
min|P|
(4)
3.1 VT-MOST
VT-MOST是一种以任务为中心的参与者选择算法,由于参与者的移动速度不同,选择候选参与者的时候不再只是根据距离最短,而是在一定距离范围内的时间最短.将最小化参与者人数作为最主要的优化目标,同时适当的考虑最小化参与者的移动总距离.先选择一个所需任务个数最多的任务作为初始任务,然后选择离该任务最近的N(N>1)位参与者作为候选参与者去完成该任务,接下来选择离初始任务最近的任务作为下一个任务(已选择过的任务或者已被完成了的任务不再被选择)……以此类推,直到得到候选参与者在指定时间内完成的任务集合.按任务个数大小比较各候选参与者所得到的任务集合,选择个数最大的那个参与者作为第一个参与者,在个数相同的情况下选择移动距离最小的那个候选参与者.已经被选择的参与者则需剔除掉,该参与者完成的任务集合相应的减少其完成任务需要的人数.以此类推,依次选出参与者完成的任务集合,直到所有任务都完成.
算法1.VT-MOST
输入:用户集合U,任务集合T
输出:参与者集合P及其完成的任务集合TU
Begin
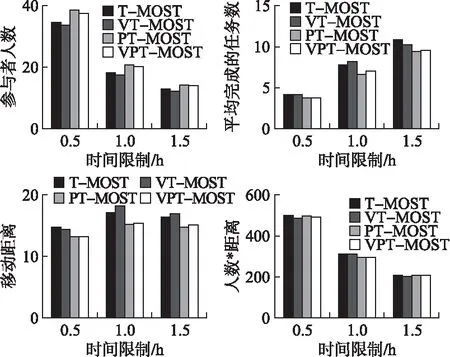
Step 1.选择剩余任务中需要人数最多的任务作为初始任务,记为tik,选择离任务tik的N-最近邻候选者中一位用户记为uij(j= Step 2.选择离任务tik最近的一个任务作为下一个任务记为ti(k+1)(k>=1). Step 3.循环执行Step 2直到参与者uij完成这些任务的时间大于h*60分钟. Step 4.输出TUij=(ti1,ti2,…). Step 5.循环执行Step 1-Step 4,选择出的每个候选者uij在h*60分钟内完成的任务集合TUij. Step 6.选择最大的TUij作为参与者uj完成的任务集合TUij. Step 7.循环执行Step 1-Step 7,确定参与者完成的任务集合. Step 8.输出参与者集合P={P1,P2,P3,…,Px}及其完成的任务集合TU={TU1,TU2,…,TUj}. End 文献[16]提出的PT-MOST算法是以参与者为中心的,由于算法运算的时间复杂度过高.当平台中候选参与者较多时,运算成本过高.本文提出的VPT-MOST采用文献[13]提出的一种将感知区域划分为一组子区域或者格子的方法.有效的降低了其运算的时间复杂度.本文中由于参与者的移动速度不同,在选择候选参与者的时候不再比较每个候选者的任务集合,而是根据各个子区域,在每个子区域中存在一个速度值最大的候选者计算其任务集合.这样通过比较候选者的任务集合确定参与者. 划分子区域,选择子区域中速度值最大的候选者,然后选择距离已选候选者最近的任务作为初始任务,接下来选择离初始任务最近的任务作为下一个任务(已选择过的任务或者已被完成的任务不再被选择),……以此类推,直到得到候选参与者在一定时间内完成的任务集合.按任务个数大小比较各个子区域中唯一的候选参与者所得到的任务集合,选择完成任务个数最大的那个候选者作为第一个参与者,若任务个数相同时选择移动距离最小的那个候选参与者.根据已选参与者完成的任务集合,剔除该参与者且该参与者完成的任务集合相应的减少其完成任务需要的人数.以此类推,依次选出参与者完成的任务集合,直到所有任务都完成. 算法2.VPT-MOST 输入:任务集合T,用户集合U 输出:参与者集合P及其完成的任务集合TU Begin Step 1.将整个感知区域划分为一组子区域,标记为tag(1-100),确定各候选者所在子区域.确定各个子区域中速度值最大的那个候选者,记为uij. Step 2.选择距离各个候选者最近的那个任务作为初始任务,记为tik. Step 3.选择离任务tik最近的一个任务作为下一个任务,记为ti(k+1)(k>=1). Step 4.直到候选参与者uij完成这些任务的时间大于h*60分钟. Step 5.输出TUij=(ti1,ti2,…). Step 6.循环执行步骤1-5,选择出每个候选者uij在h*60分钟内完成的任务集合TUij. Step 7.选择最大的|TUij|作为参与者uj完成的任务集合TUij. 循环执行步骤1-步骤7,确定参与者完成的任务集合直到任务执行完毕. Step 8.输出参与者集合P={P1,P2,P3,…,Px}及其完成的任务集合TU={TU1,TU2,TU3,…}. End 本文通过真实数据来模拟参与者、任务所在位置.实验中假设完成每个任务的时间为5分钟,假设用户移动的路线按照点到点直线进行,由于是紧急任务,所以时间设置为1小时.结合现实情况,一般人们习惯使用自己的交通工具出行,比如开车或者骑电动车.由于共享单车的出现与盛行,一些类似于学生群体的人们骑自行车出行的概率也很普遍,除此之外还有个别不会骑车的人只能步行.在这种环境中,不同的用户速度也会大不相同.考虑到这一点,本文提出利用用户近期的速度计算其速度平均值作为该平台中候选参与者的速度值.实验为了取得相对的准确性,以下结果都是通过多次实验平均而来. VT-MOST算法中选用的N值,考虑到距离、速度对于实验的综合影响,以最小化速度与距离的乘积为目标,经过多次实验确定为5.如图1所示,随着N值的增加,选择出的参与者人数与其移动的总距离的乘积先下降后上升.本文中取N=5. 图1 N值变化对VT-MOST的影响 如图2所示,参与者人数随着任务个数的增加而增加,移动距离也在不断增加.每个人完成的任务数在上下波动,呈增加趋势.图2是任务个数的变化对T-MOST与VT-MOST算法的各项性能影响的实验结果,VT-MOST算法选择出的参与者人数相对于T-MOST中的参与者人数较少,随着任务个数的增加差距更大.VT-MOST中平均每个人完成的任务个数更多,移动距离相对较远一点或者几乎接近T-MOST.VT-MOST中总距离与人数的乘积较T-MOST算法更小.如果需要参与者人数最小化VT-MOST算法更好一点. 图2 任务个数变化对算法的影响 图3比较了PT-MOST算法与VPT-MOST算法随着任务个数变化的各种变化.PT-MOST算法选择的参与者较VPT-MOST多一点,完成人数数目较少,移动距离较小或接近于PT-MOST算法. 图3 任务个数变化对算法的影响 在感知系统参与者优选方法中,候选者、任务影响着任务分配的结果.候选人数越多,选择出的参与者也更加优异.任务个数越多,选择的参与者更多,移动距离越大.如图4、图5所示,随着候选者人数增加,选择出的参与者人数会减小,移动距离减小,移动距离与参与者人数的积减小.以参与者为中心的算法所需参与者人数较多,移动距离最短.以任务为中心的算法则相反,参与者人数较少移动距离较大一点. 图4是T-MOST与VT-MOST算法的对比,随着候选者人数的增加,VT-MOST算法中选择出的参与者人数较少,平均每个人完成的任务数较大,与T-MOST相比VT-MOST移动距离在其上下波动. 图4 候选者变化对算法影响 图5比较了PT-MOST算法与VPT-MOST算法关于候选者人数变化的对比图,随着候选者人数的增加,VPT-MOST算法中选择出的参与者人数较少,平均每个人完成的任务数较大,与PT-MOST相比VPT-MOST移动距离较大一点或几乎接近. 图5 候选者变化对算法影响 本文针对的发布任务为紧急任务,所以对时间要求很严格.即时间h的选择对于实验的情况会有很大的影响,当时间为0.5小时、1小时、1.5小时时,对各种情况进行分析.由图6可知,当时间限制增加时参与者人数在不断下降,移动距离略微增加,人数与距离的乘积呈下降趋势.在各种情况下,以任务为中心的算法所需的参与者人数较多,移动距离较短.以用户为中心的算法所需的参与者人数较少,移动距离较长.四种算法的比较中,PT-MOST算法所需参与者人数最多,移动距离较短.VT-MOST算法所需的参与者人数最少,移动距离最大.VPT-MOST算法与PT-MOST参与者人数相比较少. 图6 时间限制变化对算法影响 如图7所示,随着任务个数的增加,PT-MOST的运算时间增幅很大,而VPT-MOST则缓缓上升.并且任务个数越大时PT-MOST与VPT-MOST的运行时间差值越大. 图7 任务个数对运行时间的影响 继文献[16]提出的3种参与者优选算法,本文提出另一种解决方法:VT-MOST、VPT-MOST算法,其中VT-MOST针对T-MOST做出优化.VPT-MOST针对PT-MOST做出优化,主要体现在时间复杂度.本文提出取其速度的平均值作为其速度参考值相对而言更加接近于实际情况.当候选者具有不一样的速度值时,选择参与者的时候比较的不再只是距离最近,也要考虑速度对于各候选者选择的影响.VT-MOST算法在选择用户时比较距离初始任务最近的N位候选者,在时间h的限制条件下比较N位候选者的任务个数.选择完成任务个数最大的候选者作为参与者.而VPT-MOST算法中将感知区域划分为若干个组(100个组)或者小格子,采用聚类的思想.将候选者划分为不同的组,选择各个组内速度值最大的候选者然后计算其在时间h条件限制下的任务个数,选择完成任务个数最大的候选者作为参与者.当平台中参与者人数大于小格子数时,可以减小算法迭代一次的运算时间.这样会更加优化参与者选择的过程.通过真实数据集进行实验模拟,结果表明,在很多情况下,VT-MOST算法中的参与者优选方法会使参与者人数最小化,不足之处是它的移动距离有时会相对大一些.如果希望参与者人数最小化,VT-MOST算法的性能会更好一些.相对于PT-MOST算法VPT-MOST在很大程度的减少了运算复杂度,其选择出的参与者个数也较小.但是这里速度的值只是一个近似值.在实际任务执行中,由于交通道路的堵塞、交通工具的选用等都会引起参与者的速度发生变化,具有不确定性.3.2 VPT-MOST
4 实验与结果分析
4.1 N值的选定
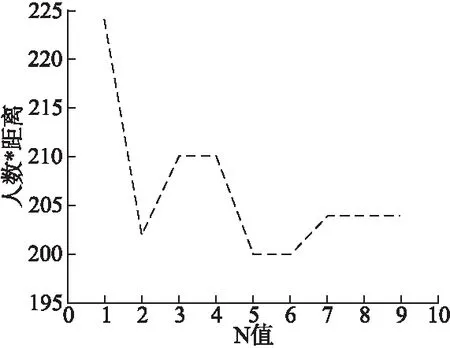
4.2 任务个数变化

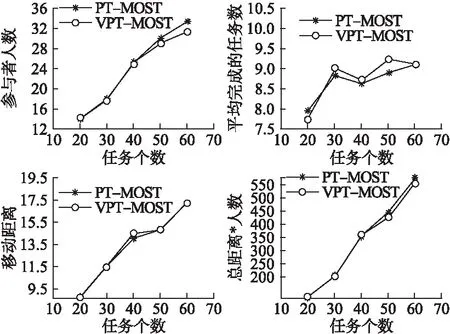
4.3 候选人数变化
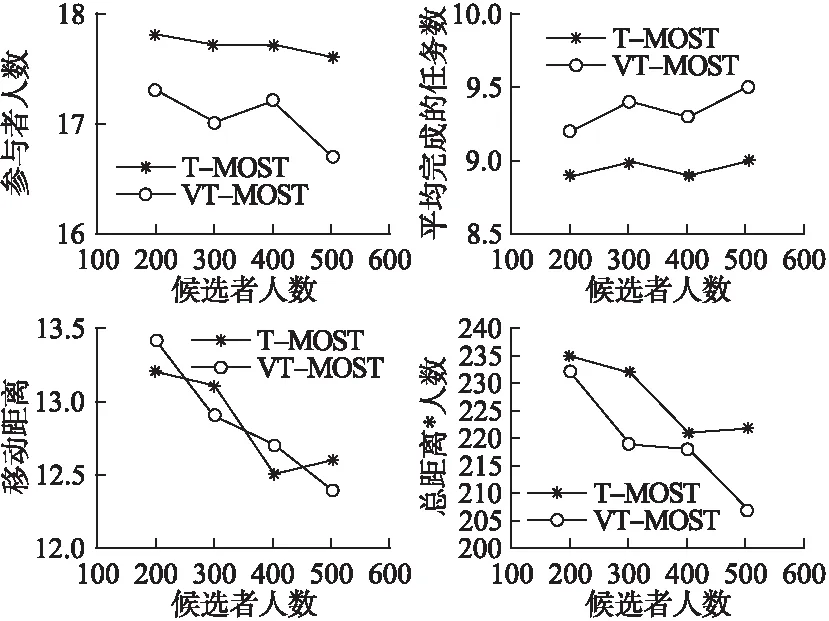
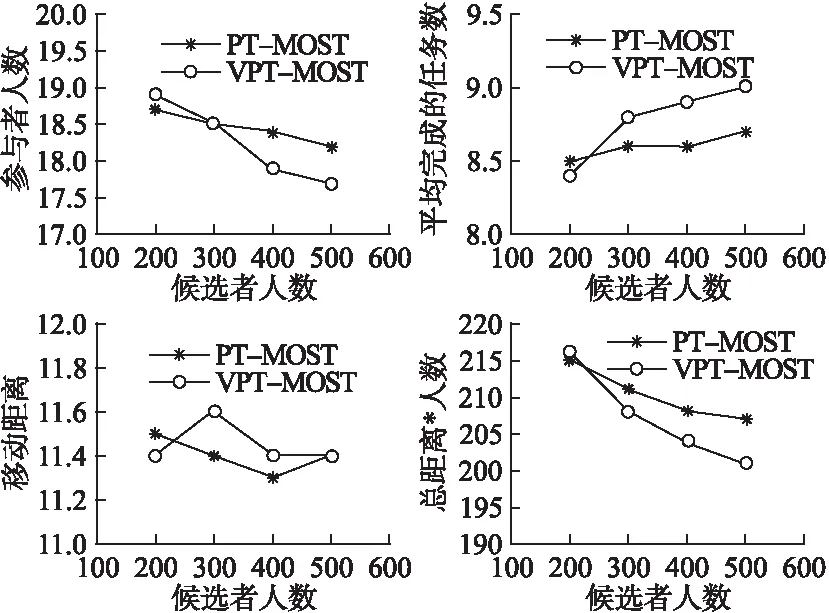
4.4 时间限制不同
4.5 时间复杂度


5 总 结
