一种双轴差动自感式传感器*

赵焕玲

(贵州职业技术学院，贵州 贵阳 550023)

0 引言

自感式传感器利用电磁感应原理将被测非电量如位移、压力、流量、振动等转换成线圈自感量(L)的变化，再由测量电路转换为电压(V)或电流(I)的变化量输出[1]。在工程应用中，通常使用两个磁回路中磁阻发生大小相等、方向相反的变化，即一个线圈的电感量增加，另一个线圈的电感量减小。在后续测量电路中，将两个电感线圈接成交流电桥的相

邻桥臂，另外两个桥臂由电阻组成，形成差动自感式传感器，从而提高差动自感式传感器灵敏度和明显改善线性度。

在工程应用中，标度因数和相位差、激励电源参数是差动自感式传感器设计的主要参数，直接影响差动自感式传感器的测量误差。另外，传感器的环境适应性是考核传感器的测量精度的重要指标，对于自感式传感器，外部电磁环境对测量精度会产生很大的影响。

1 双轴差动自感式传感器原理

一种双轴差动自感式传感器[2]主要对高速旋转的转子相对壳体的转角α和β敏感，将其转换为电量UX、UY并输出。其结构原理及测量线路见图1。

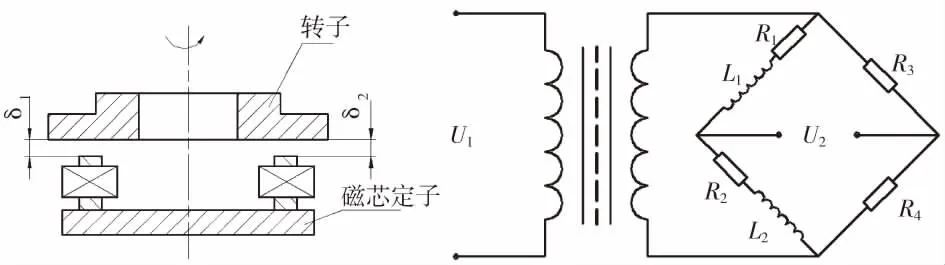
图1 自感式传感器结构原理图及测量线路Fig.1 Structure and measuring circuit of the self-induction sensor

在转子端面上装有一个用软磁材料铁铝系磁性合金制作的导磁环，作为闭合回路的一部分，同时在转子上安装有高磁场强度的永久磁钢，这将对自感式传感器产生反作用力矩。四个用精密磁性材料叠片制成的U型铁芯，等间隔(90°)均匀粘接在磁芯定子上，在每个铁芯上安装两个激磁线圈串联组成的电感线圈，在垂直于旋转轴的平面上，交叉相对的两个带有激磁线圈U型铁芯通过两个空气隙和导磁环构成闭合回路，U型铁芯上的线圈与两个桥臂电阻构成一个轴向的差动式电感传感器。四个U型铁芯上的线圈与相对应的两个桥臂电阻构成了双轴差动式自感式传感器[3]。

对其中一轴的差动式自感式传感器，当转子轴偏转角α为零时，图1中测量电桥处于平衡状态，即δ1=δ2=δ0，感抗X1=X2，则差动式自感式传感器测量线路输出电压U2=0，当转子转动α角时，δ1减小，δ2增大，致使差动式自感式传感器同轴方向上的两个线圈的感抗X1和X2发生变化，X1>X2，电桥的平衡被破坏，差动式自感式传感器测量线路输出一个与转子轴转角成比例的电压信号U2，另一轴向的传感器原理相同。

2 双轴差动自感式传感器标度因数及相位差[4]

双轴差动自感式传感器电感变化量ΔL与间隙变化量Δδ的关系见下式：

式中：W为铁芯上总的线圈匝数；S为定转子之间气隙总面积(m2)；ω0为气隙磁导率(H/m2)，U0=4π×10-7H/m2。

当激磁电源频率f足够高(10～20 kHz)，电感线圈的品质因数Q=2πfL/R足够大时(式中L与R分别为电感线圈的电感和电阻)可近似略去电阻值，见图2。

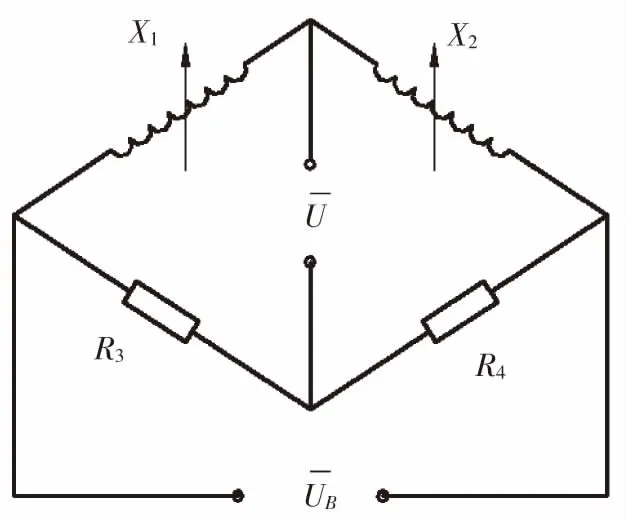
图2 差动自感式传感器测量电桥Fig.2 Measuring electric bridge of the dual-axisself-induction differential sensor

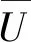
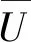
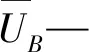
另有：

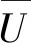
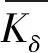
式中：l为敏感元件中心线到转子中心距的距离(m)。

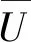
因为

L1=L0+ΔL1，L2=L0-ΔL2

则L1+L2=2L0+ΔL1-ΔL2，L1-L2=ΔL1+ΔL2，

所以，测量线路输出电压为：

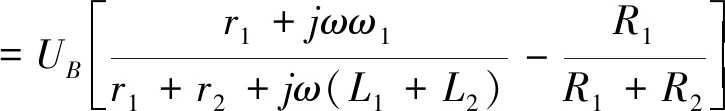
因此，传感器输入-输出相位差φ为：

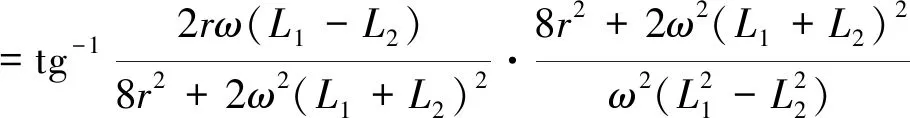
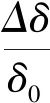
图2测量电路传统的连接方式：采用电感桥臂即X1、X2中间抽头接电路零位，这种方式需要调节导磁环，让两端的间隙(机械零位)最小，而实际状态导磁环的位置是随机而不能调节，因此差动自感式传感器试验中的零位与实际状态的零位不一致，而采用电感桥臂即X1、X2中间抽头接电路输入测量，在差动自感式传感器试验中和实际状态零位一致，而且差动自感式传感器试验中导磁环的位置随机转换适当角度，测得的零位都不变。

3 差动自感式传感器电磁反作用力矩

在工程应用中，差动自感式传感器与由钐钴磁材料制作的永磁铁装配在同一个转子上，距离很近，磁感应强度高的永磁体产生磁场对的铁芯、导磁环之间不可避免产生电磁反作用力矩误差。其电磁反作用力矩见下式。

式中：s—定转子之间气隙总面积(m2)；UB—激励电压(V)；ω—励磁频率(Hz)；Ks—漏感系数；α—飞轮偏转角(rad)。

由上式可知，适当提高激励频率，降低激励电压，均能有效减少由电磁反作用力矩引起的测量误差。

4 工程计算分析

理论分析和实践都表明，漏磁阻对传感器标度因数的影响是不可忽略的，这是因为气隙长度与铁芯截面面积相比并非充分小，究竟小多少取决于传感器的结构型式以及气隙长度与铁芯截面面积大小，实际计算时可将计算所得到的kv值乘以一个小于1的系数k′就得到经过修正的传递系数Kv，即

在工程设计应用中，差动自感式传感器采用2 V，20 kHz的激磁电源，单个铁芯截面面积：

s=4 mm，l=11×10-3mm。W=900匝，Ks=0.4，Δδ=0，则ΔL1=ΔL2=0，即ΔL=0，ΔL1=ΔL2=L0，取K′=0.6，得：

电磁反作用力矩：

=1.6×10-11(N·m)

当转子轴没有偏转，差动自感式传感器平衡位置电感量L0：

差动自感式传感器标度因数：

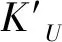
=4(mV/C)

差动自感式传感器输入-输出相位差：

由于输出电压U是由同变压器输出电压UB同相位的分量和正交分量部分组成，因为电压UB是一定的，所以当转子转角方向改变时，U便反相。输出电压U总是比变压器输出电压UB滞后：

差动自感式传感器工作时输出滞后相位差应比它相对的平衡位置输出相位差小，在小角度工作情况下，Δδ2为无穷小量，可忽略不计，因此：

在实际应用中，因为气隙长度与铁芯截面面积相比并非无穷小，漏磁阻及漏感抗的影响是不能忽略的，若考虑漏磁阻及漏感抗，线圈磁阻将增大，而实际电感比平衡位置所计算的电感小，另外，随着温度的升高，线圈电阻还会增加，整个差动自感式传感器输出相位差应较平衡位置输出相位差大[6]。

另外，差动自感式传感器测量电桥为理想的完全对称，即输出电压U=0的条件是r1=r2，R1=R2，及L1=L2，实际上，两个传感器的几何尺寸，线圈匝数和阻抗以及导磁材料的性能等都不可能做到理想对称，铁芯短路、线圈匝数短路和分布参数的不同影响更增加了两传感器的电磁参数的不对称的程度，且两个桥臂电阻R1和R2也不可能完全对称，还有漏感、磁滞损耗等都对双轴差动自感式传感器测量精度有影响。

5 结论

通过对双轴差动自感式传感器的标度因数和相位差，测量电路的分析计算，气隙长度与铁芯截面面积，以及铁芯短路，线圈匝数短路和分布参数影响都会影响双轴差动自感式传感器测量精度。同时，对电磁反作用力矩等进行分析，采取提高激磁频率、降低激磁电压的方案，有利于双轴差动自感式传感器零位的调节，减小由于电磁力矩带来的测量误差。