削边形式对筒体与封头过渡区应力分布的影响
2020-09-02王战辉马向荣宋俊汶
王战辉 马向荣 党 睿 高 浩 宋俊汶
(1.榆林学院化学与化工学院;2.陕西省低变质煤洁净利用重点实验室)
随着我国化工行业的迅速发展,对于压力容器的需求也越来越大,压力容器作为化学工业中重要的特种设备,多处于高温和高压的工作环境中,因此它的安全性备受关注[1]。筒体和封头作为压力容器主要承压元件,其承压性能对压力容器的正常运行起着至关重要的作用,筒体和封头之间一般采用焊接连接, 而且筒体和封头的厚度、材料大多不同,所以筒体和封头连接区域既要承受内部载荷、外部载荷,也要承受焊接应力和不连续应力[2]。其中,不连续应力是由结构不连续引起的。 如前所述,筒体和封头的厚度、曲率半径和材料不一致, 均会引起几何形状不连续的现象,在边缘力和边缘力矩的共同作用下,产生不连续应力(薄膜应力和弯曲应力),这两部分应力均叠加在由内压或外压引起的两向应力上,从而使筒体和封头连接区域最大等效应力增大,危险性增加[3]。常见的凸形封头包括半球形封头、椭圆形封头及无折边球形封头等,凸形封头由于应力分布均匀在实际生产当中占据着主导地位,因此如何减小筒体和凸形封头过渡区域最大应力成为亟待解决的问题。
在实际生产中,凸形封头与筒体的连接通常采用减薄筒体的方法,即对筒体削边[4,5]。 根 据GB 150—2011 标准,筒体与封头过渡区域可以分为6 种连接削边形式,国内外很多学者都是对前3 种连接削边形式(形式a、b、c)进行应力分析和评定,而对后3 种连接削边形式(形式d、e、f)还没有进行研究[6~8]。因此,笔者以半球形封头、椭圆形封头和无折边球形封头3 种凸形封头为研究对象,利用ANSYS 16.0 有限元分析软件,得到应力分布云图, 并通过改变削边长度和削边形式,考察其应力分布规律,并进行优化分析。
1 设计参数
半球形封头压力容器的设计参数:设计压力p为6MPa,设计温度T为200℃,材料为Q460,弹性模量E为206GPa,泊松比为0.28。 筒体内半径R1为500mm,筒体壁厚t1为100mm,筒体长度H为800mm,半球形封头内半径R2为550mm,封头壁厚t2为60mm,削边长度L 为150mm。
椭圆形封头压力容器的设计参数: 设计压力p为6MPa,设计温度T为200℃,材料为Q460,弹性模量E为206GPa, 泊松比为0.28。 筒体内半径R1为500mm, 筒体壁厚t1为100mm, 筒体长度H 为800mm,椭圆形封头长半轴a为550mm、短半轴b为275mm,封头壁厚t2为60mm,削边长度L为150mm。
无折边球形封头压力容器的设计参数:设计压力p为6MPa, 设计温度T为200℃, 材料为Q460,弹性模量E为206GPa,泊松比为0.28。筒体内半径R1为500mm,筒体壁厚t1为100mm,筒体长度H为800mm, 无折边球形封头内半径R2为550mm,封头曲面深度h为175mm,封头壁厚t2为60mm,削边长度L为150mm。
2 有限元分析
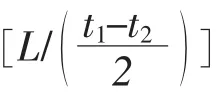
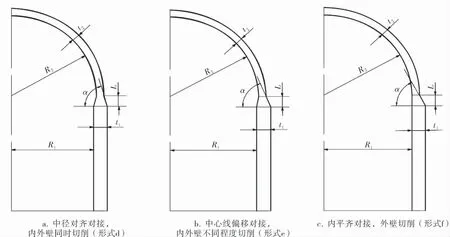
图1 半球形封头与3 种削边形式的结构示意图
3 种封头形式的压力容器除承受内压p 之外,还应考虑外压载荷、风载荷及地震载荷等因素的影响,但是其他因素与内压p 比较,可以忽略不计。因此,只考虑内压p 的影响。在几何对称面施加对称位移约束,在封头和筒体内表面施加内压p,其中,内压p 为6MPa,即可得到其应力云图[9,10]。 筒体和封头的厚度与内径相比要小得多,因此可视为薄壁容器,只承受经向应力和周向应力。
2.1 半球形封头应力分布
以内外壁同时切削为例,半球形封头压力容器两向应力分布如图2 所示,最大应力主要集中在封头和筒体的过渡段,为几何形状不连续产生的边缘应力,其他部分应力分布较均匀,为内压引起的薄膜应力。 削边长度L分别取120、150、180、210、240、270、300mm, 考察削边长度L对最大等效应力的影响,引入应力集中系数K(K=σmax/σθ,σmax表示封头和筒体连接区域最大等效应力,σθ表示周向薄膜应力、σθ=pR2/2t2)。
改变削边长度L, 考察削边长度L 对不同削边形式球形封头压力容器的应力集中系数K 的影响(表1)。由表1 可见,不同削边长度和削边形式下,应力集中系数不同。 半球形封头与筒体内平齐对接, 外壁切削的应力集中系数K 最小;半球形封头与筒体中心线偏移对接,内外壁不同程度切削的应力集中系数K 最大。 另外,对于削边长度L 还需使用ANSYS 软件继续下一步的优化分析。
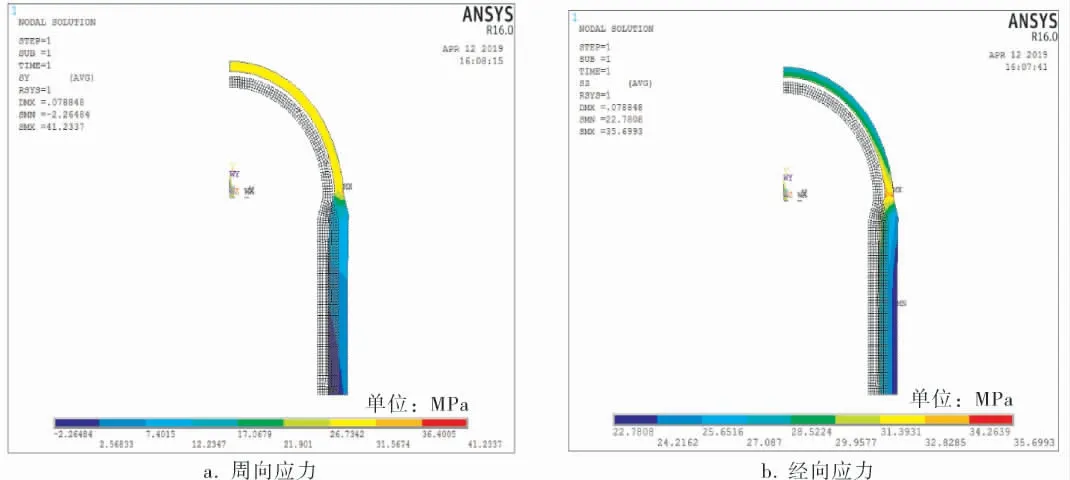
图2 内外壁同时切削的半球形封头压力容器两向应力分布云图
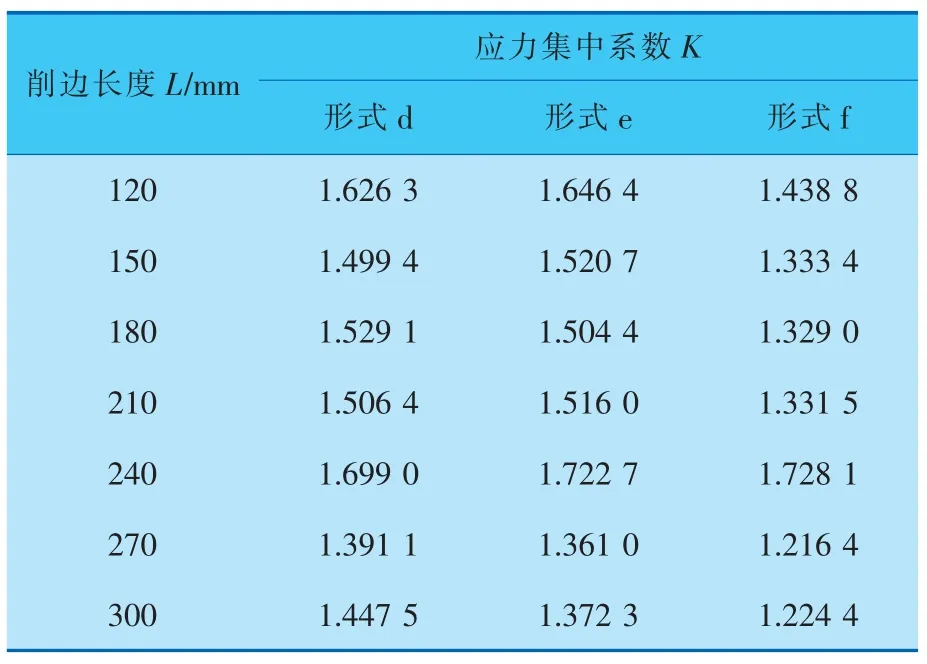
表1 不同削边形式半球形封头压力容器应力集中系数
2.2 椭圆形封头应力分布
以内外壁同时切削为例,椭圆形封头压力容器两向应力分布如图3 所示,最大应力主要集中在封头和筒体的过渡段,为几何形状不连续产生的边缘应力,其他部分应力分布较均匀,为内压引起的薄膜应力。 削边长度L 分别取120、150、180、210、240、270、300mm,考察削边长度L 对最大等效应力的影响,同样引入应力集中系数K。
改变削边长度L, 考察削边长度L 对不同削边形式椭圆形封头压力容器的应力集中系数K的影响(表2)。由表2 可见,不同削边长度和削边形式下,应力集中系数不同。 椭圆形封头与筒体内平齐对接, 外壁切削的应力集中系数K 最大;中径对齐对接,内外壁同时切削的应力集中系数K 最小; 而椭圆形封头与筒体中心线偏移对接,内外壁不同程度切削的应力集中系数K 处于二者之间。 另外,对于削边长度L 还需使用ANSYS软件继续下一步的优化分析。
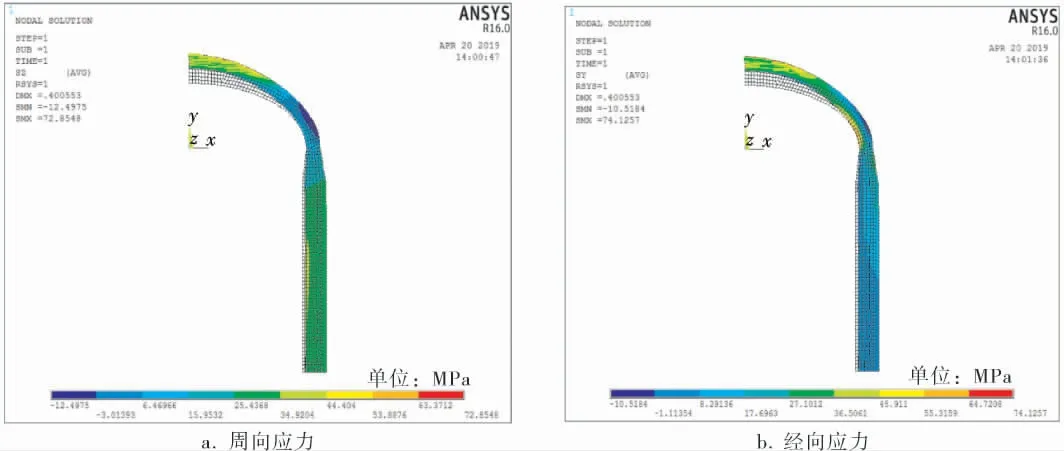
图3 内外壁同时切削的椭圆形封头压力容器两向应力分布云图
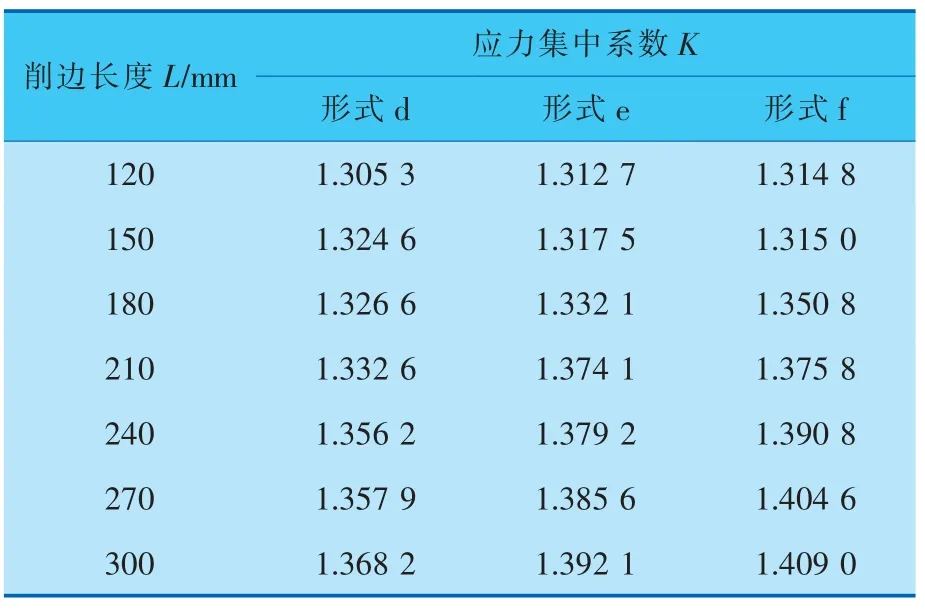
表2 不同削边形式的椭圆形封头压力容器应力集中系数
2.3 无折边球形封头应力分布
以内外壁同时切削为例,无折边球形封头压力容器两向应力分布云图如图4 所示,最大应力主要集中在封头和筒体的过渡段,为几何形状不连续产生的边缘应力, 其他部分应力分布较均匀,为内压引起的薄膜应力。 削边长度L 分别取120、150、180、210、240、270、300mm,考察削边长度L 对最大等效应力的影响,同样引入应力集中系数K。
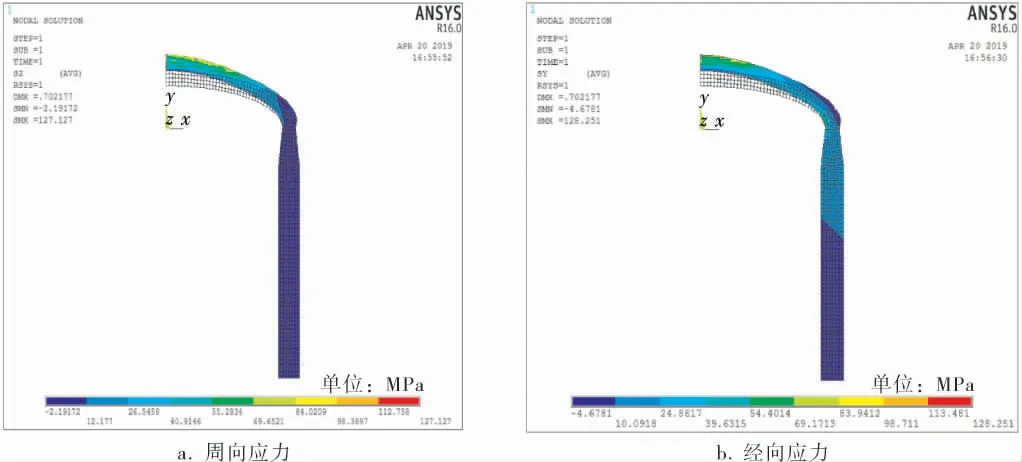
图4 内外壁同时切削的无折边球形封头压力容器两向应力分布云图
改变削边长度L, 考察削边长度L 对不同削边形式无折边球形封头压力容器的应力集中系数K 的影响(表3)。 由表3 可见,不同削边长度和削边形式下,应力集中系数不同。 无折边球形封头与筒体内平齐对接,对外壁进行切削应力集中系数K 最大;中径对齐对接,内外壁同时进行切削应力集中系数K 最小;而无折边球形封头与筒体中心线偏移对接,内外壁不同程度切削应力集中系数K 处于二者之间。 另外,对于削边长度L 还需使用ANSYS 软件继续下一步的优化分析。
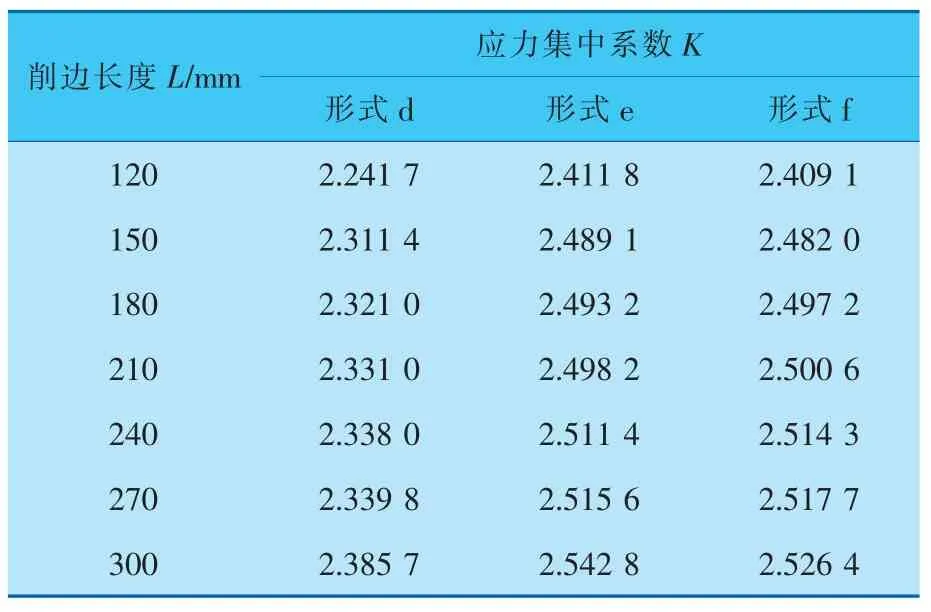
表3 不同削边形式无折边球形封头压力容器应力集中系数
综合上面的数据分析,在相同尺寸和相同削边形式下,半球形封头压力容器应力集中系数和最大应力值最小,而无折边球形封头压力容器应力集中系数和最大应力值最大;而在半球形封头中,封头与筒体内平齐对接,对外壁进行切削削边形式下应力集中系数最小。
3 优化分析
由上述分析可知,筒体的削边长度并不是随意取值的,一定范围内,其最大应力值和应力集中系数较小,而当超过此范围,最大应力值和应力集中系数就会急剧变大,导致发生损坏,因而有必要进行优化分析。 具体优化过程为:令斜边倾斜角α=90°-arcsin(L/R2)为状态变量、应力集中系数K=σmax/σθ为目标函数、 筒体的削边长度L≥3Y(Y=R1+t1-R2-t2)为设计变量,以削边长度L=150mm 为例,对封头与筒体中径对齐对接、内外壁同时切削的压力容器类型进行优化,循环次数设置为20。
3.1 半球形封头压力容器
对于半球形封头压力容器, 中心线偏移对接、 内外壁不同程度切削的应力集中系数K 最大,故对该削边形式进行优化。 应力集中系数随削边长度的变化曲线如图5 所示,应力集中系数随循环次数的变化曲线如图6 所示。利用ANSYS软件对其削边长度进行优化,相关参数均发生大的变化:削边长度L 由先前的150.000mm 增大到164.740mm,筒体的削边倾斜角α 由72.542°缩小到70.763°; 应力集中系数K 从1.499 4 下降到1.084 6,下降率达到27.664%,达到实际优化效果。
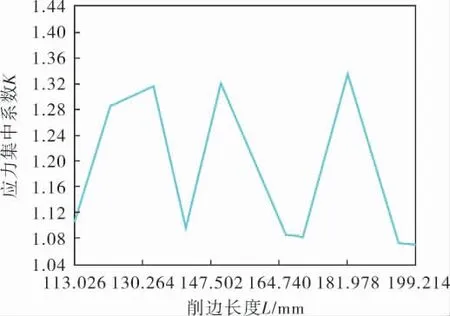
图5 应力集中系数随削边长度的变化曲线

图6 应力集中系数随循环次数的变化曲线
3.2 椭圆形封头压力容器
对于椭圆形封头压力容器,封头与筒体内平齐对接、外壁切削的应力集中系数K 最大,故对该削边形式进行优化。 应力集中系数随削边长度的变化曲线如图7 所示, 应力集中系数随循环次数的变化曲线如图8 所示。 利用ANSYS 软件对其削边长度进行优化,相关参数均发生大的变化:削边长度 L 由先前的 150.000mm 增大到176.264mm, 筒体的削边倾斜角α 由74.176°缩小到71.308°; 应力集中系数K 从1.325 6 下降到1.137 5,下降率达到14.190%,达到实际优化效果。

图7 应力集中系数随削边长度的变化曲线

图8 应力集中系数随循环次数的变化曲线
3.3 无折边球形封头压力容器
对于无折边球形封头压力容器,封头与筒体内平齐对接、 外壁切削的应力集中系数K 最大,故对该削边形式进行优化。 应力集中系数随削边长度的变化曲线如图9 所示,应力集中系数随循环次数的变化曲线如图10 所示。 利用ANSYS 软件对其削边长度进行优化,相关参数均发生很大变化: 削边长度L 由先前的150.000mm 增大到163.252mm,筒体的削边倾斜角α 由74.176°缩小到72.736°; 应力集中系数K 从2.311 4 下降到1.679 5,下降率达到27.070%,达到实际优化效果。

图9 应力集中系数随削边长度的变化曲线
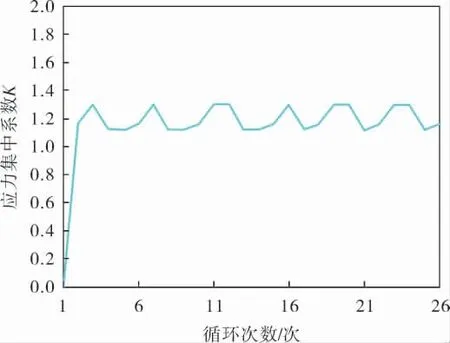
图10 应力集中系数随循环次数的变化曲线
3.4 数据汇总比较
将上述3 种不同封头形式的压力容器优化数据进行汇总后列于表4。由表4 可见,半球形封头压力容器应力集中系数K 最小、优化效果最为明显。
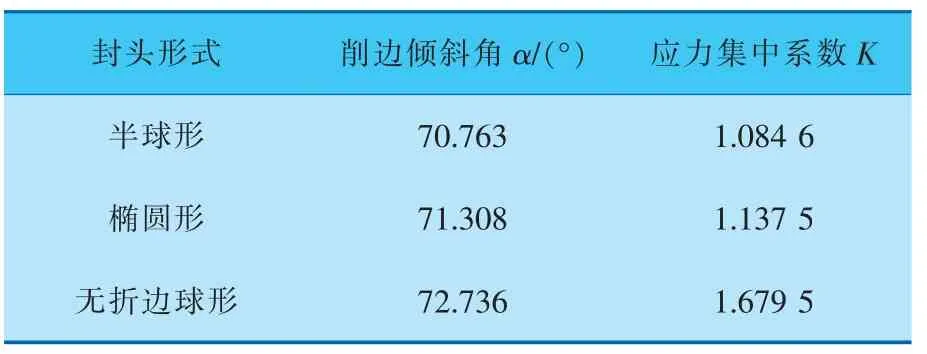
表4 不同类型的压力容器有限元优化后参数对比
4 结论
4.1 3 种封头形式压力容器的最大等效应力集中于筒体和封头过渡区域,属于危险区域,容易发生强度失效。
4.2 在相同尺寸和削边形式下,半球形封头压力容器的应力集中系数和最大应力值最小,无折边球形封头压力容器的应力集中系数和最大应力值最大;在半球形封头中,封头与筒体内平齐对接、外壁切削的削边形式应力集中系数最小。
4.3 随着削边长度L 的增加, 椭圆形封头和无折边球形封头压力容器应力集中系数K 均呈增大的趋势, 而半球形封头压力容器的削边长度L出现临界值。
4.4 对3 种封头形式的压力容器进行优化,优化后半球形封头压力容器的应力集中系数K 最小、优化效果最为明显。
