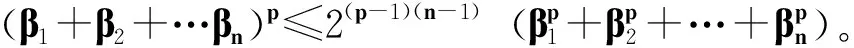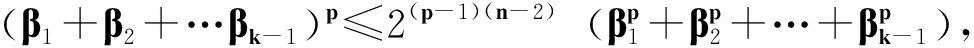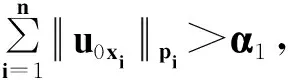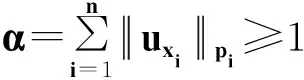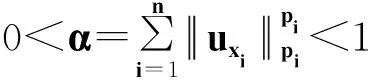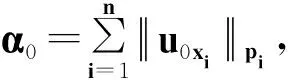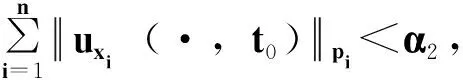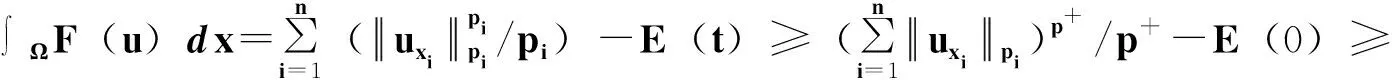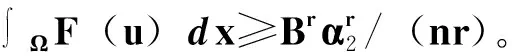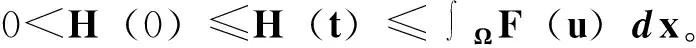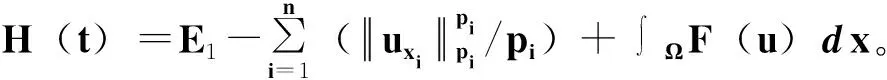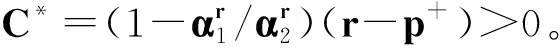各向异性的非线性抛物方程解的爆破
2020-09-01杨晓菊詹华税
杨晓菊,詹华税
(1.集美大学理学院,福建 厦门 361021;2.厦门理工学院应用数学学院,福建 厦门 361024)
0 引言
各向同性和各向异性都是宏观尺度,是物质材料的自身的属性,跟材料的尺度大小、内部原子排列结构、分子相互作用等密切相关。通俗来讲,各向异性就是在各个方向上所体现出来的性质都不一样。各向异性的抛物方程与p-Laplace方程具有本质的区别,它可以用来描述一些特殊的电阻原件,它们正接是良导体,反接就是绝缘体或者电阻很大,各个方向上的电导的物理常数差异很大。近些年来,越来越多的学者们对各向异性的内容很感兴趣,并做了相关的研究[1-3]。
(1)
其中:Ω是Rn中一个有界区域,且有光滑边界∂Ω;2 文献[4]给出了方程(1)各向同性解的爆破,文献[5]将其结果推广到p(x)的情形。本文主要是借用文献[4]的方法,运用一定的计算技巧,得到各向异性的非线性抛物方程解的爆破性。 性质1W1,p(Ω)是可分的、自反的Banach空间。 (2) (3) 令α1=B-r/(r-p+)n1/(r-p+)2(1-p+)(n-1)/(r-p+),E1=(1/p+-1/r)B-rp+/(r-p+)np+/(r-p+)2r(1-p+)(n-1)/(r-p+),且 (4) (5) 为了证明定理1,首先引入如下引理。 引理1 设函数g:[0,∞)→R且定义:g(α)=2(1-p+)(n-1)αp+/p+-Brαr/(nr), 0<α<1;g(α)=2(1-p+)(n-1)αp-/p+-Brαr/(nr),α≥1,那么函数g(α)具有如下性质:1)当0<α<α1时,函数g是单调递增的,当α>α1时,函数g是单调递减的;2)当α→ +∞时,g(α)→-∞;3)g(α1)=E1,α1∈(0,1)。这里α1和E1由前文给出。 证明这里的证明类似于文献[4]。 命题1 设p≥1,那么对于任意的非负数a和b,有(a+b)p≤2p-1(ap+bp)。 (6) (7) (8) (9) 引入如下函数H(t)=E1-E(t),∀t≥0。 (10) (11) (12) 证毕。 (13) 那么,由式(4)和式(10)可以得到 (14) (15) (16) (17) 结合式(16)和式(17),有G′(t)≥ηGr/2(t)。 (18) 其中,η=C*/(rC)。 对式(18)积分得Gr/2-1(t)≥1/[G1-r/2(0)-(r/2-1)ηt]。 (19) 因此,G在t*≤Gr/2-1(0)/[(r/2-1)η]时爆破。定理1得证。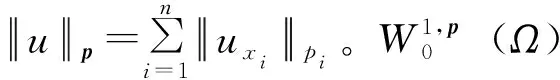
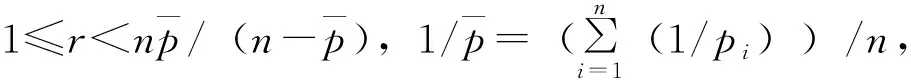
1 主要结果
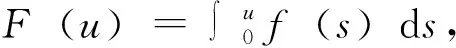
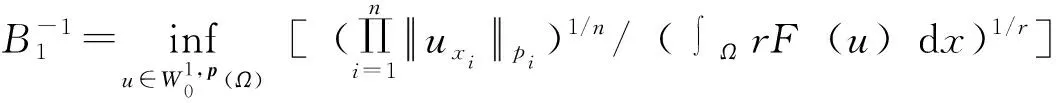
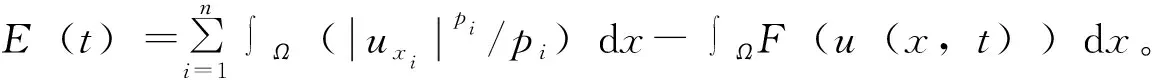
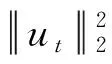
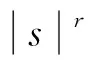

2 定理1的证明