量子计算在增量式大数据并行挖掘中的应用
2020-09-01李晓峰王妍玮
李晓峰, 王妍玮, 李 东
(1. 黑龙江外国语学院 信息工程系, 哈尔滨 150025; 2. 普度大学 机械工程系, 印第安纳州 西拉法叶市 IN47906; 3. 哈尔滨工业大学 计算机科学与技术学院, 哈尔滨 150001)
0 引 言
大数据本身是一个比较抽象的概念, 主要指需要新处理模式才能具有更强的决策力、 洞察力和流程优化能力的改良、 高增长率和多样化的信息资产。由于在互联网大数据中能描绘出具体的数据特征, 因此对其进行数据挖掘具有较大的研究价值。在通常情况下大数据具有数据体量大、 数据类型繁多、 处理速度快以及价值密度低的特点, 因此在对其挖掘过程中需要经过几个基本的挖掘步骤, 才能得到最终结果。通常在数据挖掘过程中, 首先进行数据采集, 然后通过数据清理、 集成、 归约以及变换等步骤, 完成数据的预处理过程, 最终经过特征提取与处理、 数据建模与转换, 输出数据挖掘的最终评估结果。由于其数据信息不是静态的, 而是以增量式形式逐渐增加的, 因此为了提高数据挖掘效率, 近些年人们提出了并行数据挖掘技术, 通过将顺序执行的计算任务分解成多个可以同时执行的子任务, 并且其可以同时并行执行, 最终完成整个计算任务。
量子算法是一种遵循量子力学规律调控量子信息单元进行计算的新型计算模式, 张焕国等[1]主要分析了量子问题、 量子线路及量子算法复杂性的有关问题, 对量子环境下的算法设计和问题求解具有指导意义; 孙晓明[2]围绕着量子算法、 计算复杂性、 程序理论、 电路和密码学, 对近些年来量子力学理论展开研究与总结, 并展望了未来量子算法的发展方向; 许精明等[3]根据量子算法具有计算灵活, 结果准确的优点, 将量子算法应用于网络节点扩展的酉变换矩阵的研究中; 金贻荣等[4]主要研究了超导量子计算在抑制电荷、 磁通和准粒子等几种主要噪声来源方面做出探索; 张兰等[5]主要对量子粒子群优化算法进行了研究; 周海鹏等[6]主要研究了自适应混沌量子粒子群算法及其在WSN(Wireless Sensor Network)覆盖优化中的应用; 张惠珍等[7]在传统量子算法的基础上, 利用量子蚁群算法分析了多车次同时送取货物车辆路径问题。
诸多专家学者对增量式大数据并行挖掘方法进行了研究, 并取得了一定的研究成果。文献[8]提出一种基于MapReduce的并行频繁模式增量挖掘算法。由于传统的频繁模式挖掘算法是以“批处理”方式执行的, 即一次性对所有数据进行挖掘, 无法满足不断增长的大数据挖掘的需要, 因此引入MapReduce, 将传统频繁模式增量挖掘算法CanTree向MapReduce计算模型进行了迁移, 实现了并行的频繁模式增量挖掘。文献[9]提出一种大数据环境下关联规则并行分层挖掘算法, 将整个数据库D随机分割成若干个非重叠区域, 并行挖掘出局部频繁项集, 利用先验性质连接局部频繁项集得到全局候选项集, 再次扫描D统计出每个候选项集的实际支持度, 以确定全局频繁项集, 以此实现大数据并行挖掘。文献[10]提出了时空大数据背景下并行数据处理分析挖掘方法, 以其作为研究基础, 重点从时空大数据的存储管理、 时空分析和领域挖掘3个角度对并行化挖掘方法进行了设计。
经过研究发现, 上述并行式数据挖掘方法无法考虑到大数据增量变化的问题, 在增量式大数据中召回率低, 不能全面且准确地挖掘大数据中的数据信息。为解决上述问题, 笔者在传统并行数据挖掘的基础上, 引入量子算法, 提出基于量子算法的增量式大数据并行挖掘方法。将量子算法应用于大数据挖掘方法的优势在于打破了图灵机模式的计算限制, 提高指数效率和计算性能, 以达到保证增量式大数据并行挖掘的基础上实现大数据的精准挖掘。
1 构建增量式大数据并行挖掘模型
按照大数据并行挖掘的基本流程搭建相应的并行数据挖掘模型, 并在模型中引入量子算法, 其模型的搭建结果MapReduce如图1所示。图1中并行数据挖掘模型实现的基本过程一般有: 数据准备、 开采、 评估与表示等。通过该模型, 大数据并行挖掘的相关程序将被自动的分布到一个由普通机器组成的超大机群上并发执行, 而模型中的Map和Reduce分布为该模型中的两大基本操作, 分别表示数据挖掘中的映射过程和归约过程。Map任务在执行过程中需要将一组数据一对一的映射到另外一组数据中, 而Reduce利用映射规则与归约规则实现数据聚类挖掘[11]。两个步骤程序通过把大数据的操作分发给网络上的每个节点, 实现数据的并行式挖掘, 每个节点以周期性的运行方式, 将计算得到的结果和状态信息返回到主节点中。

图1 数据挖掘模型Fig.1 Data mining model
2 量子算法数据预处理
量子计算是综合利用量子力学原理和计算机科学相关知识进行计算的一种新的计算模式。在现阶段利用量子机制进行信息处理已成为突破经典计算极限的一条重要的探索途径, 量子计算建立在与传统比特概念类似的量子比特上, 主要利用量子系统的叠加性、 纠缠性和相干性等实现量子的并行计算。
通过量子算法进行数据的预处理, 将计算模型上的数据进行移植, 使用3个MapReduce任务实现并行挖掘预处理。预处理基本原理如图2所示。

图2 量子算法基本原理图Fig.2 Basic principle of quantum algorithm
在图2中, 不同结点按照其性质划分至不同组别, 结点所对应的组别不是唯一的, 属于一对多关系, 体现了量子纠缠性。对大数据进行数据分区与并行计数, 获取大数据频繁项集合, 进而将该集合分为局部频繁项与全局频繁项, 体现了数据之间的关联性, 说明其具有量子相干性。在对大数据处理过程中, 其频繁项可以处在不同量子态的叠加态上, 因此体现了量子叠加性。
按照图2中的量子算法原理, 使用HDFS(Hadoop Distributed File System)将大数据进行自动分配, 在第1个任务执行中对所有数据项进行并行计算, 得到所有频繁项的集合, 记为FList。将分组过的频繁项集合记为组列表GList。将包含组列表的集合进行加载启动, 并对执行结点进行数据分片处理, 输出每组关联事物结果。最后将所有的局部频繁项合并在一起得到全局频繁项集, 即为大数据挖掘的预处理结果。按照量子算法的基本计算原理[12], 对预处理步骤进行具体分析。
2.1 量子比特的数据信息转换
量子算法在应用处理过程中只能针对量子比特数据进行计算, 量子比特也是量子算法中存储信息的位移格式。因此需要将大数据中的数据信息转换成量子比特下的单位格式, 用于描述量子线路的状态信息, 因此首先对量子比特进行定义。根据量子力学的基本原理, 将量子比特的状态定为0态或1态。此外, 量子比特的状态也可以落在0态和1态之外, 可以是任意线性叠加的状态[13]。1个n位的量子存储器可以处于2n个基态的相干叠加态|φ〉中, 由此便可以同时存储2n个不同数字, 对量子寄存器进行一次操作就相当于对传统计算机的2n次操作实现并行挖掘。其中相干叠加态|φ〉可表示为
|φ〉=α|0〉+β|1〉
(1)
其中α和β分别表示一对复数, 即量子态的概率幅值[14]。α和β需要满足

(2)


(3)
其中θ与φ定义了三维单位球面上的一点P, 如图3所示。
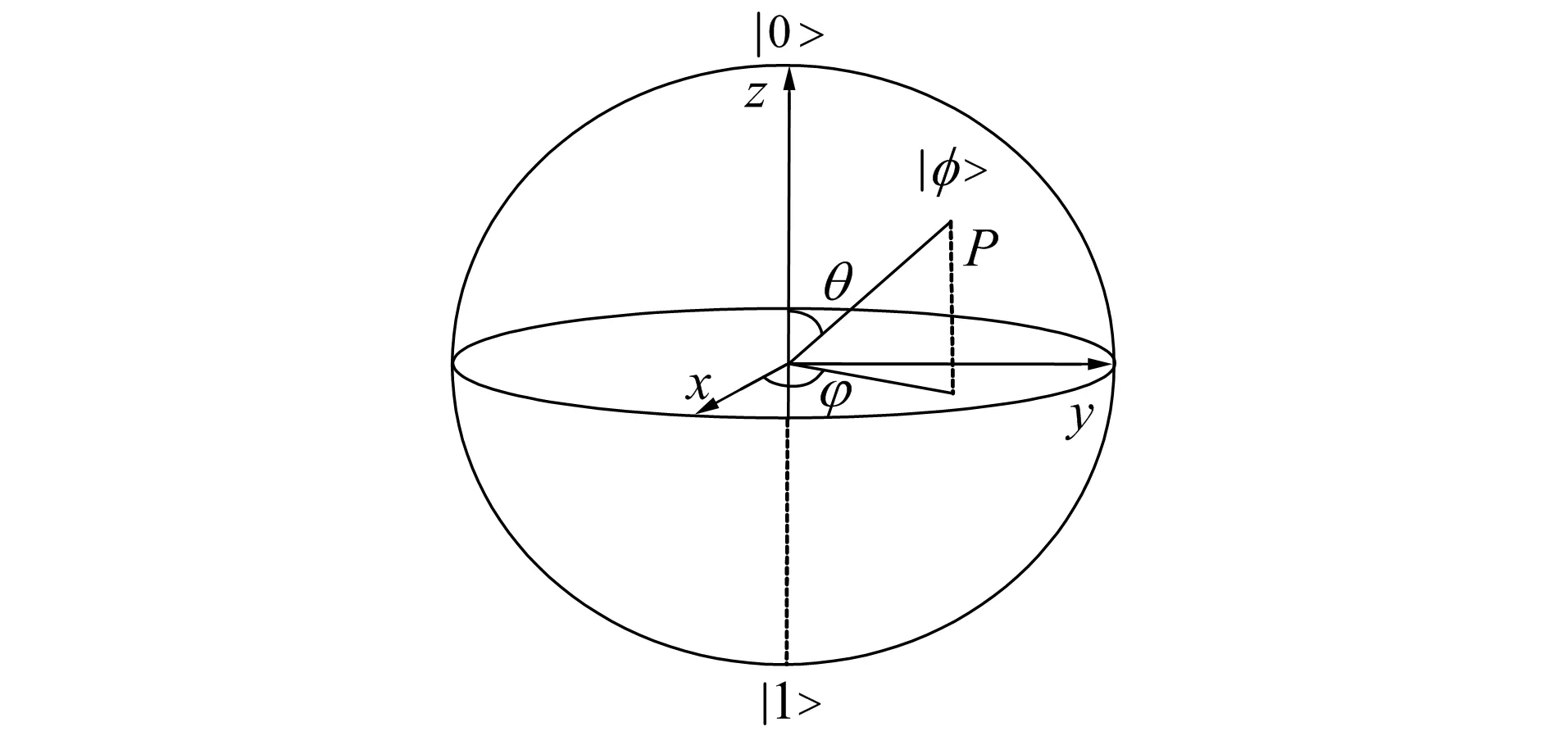
图3 量子比特坐标示意图Fig.3 Schematic diagram of qubit coordinates
将量子比特定义在球面上使单个量子比特状态可视化, 方便进行量子计算与量子信息识别, 以此实现量子比特。
2.2 量子搜索算法
在量子算法实际应用过程中难以做到使搜索概率达到100%, 且量子相位旋转角的误差会导致搜索概率下降, 因此要对量子搜索算法进行改进。设量子搜索算法初始状态为Ψmφ, 经过m迭代后得到

(4)
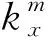
搜索过程中的相位旋转角θ是影响量子搜索算法性能的主要因素, 因此利用
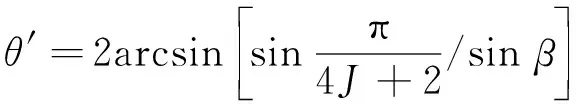
(5)
对其进行改进, 其中J为量子理想态数。
设大数据并行挖掘中的待挖掘数据的标记态为|s1〉,|s2〉,…,|sM〉, 而非标记态用|t1〉,|t2〉,…,|tN-M〉, 将对应系数代入可得
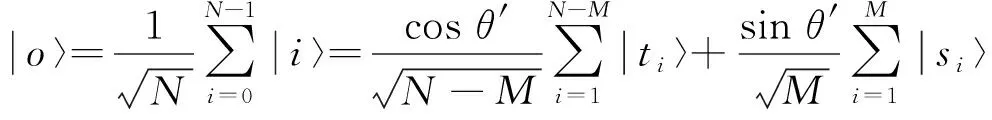
(6)
将两个相移算子Is与I0进行推广描述, 可将量子搜索[15]结果描述为
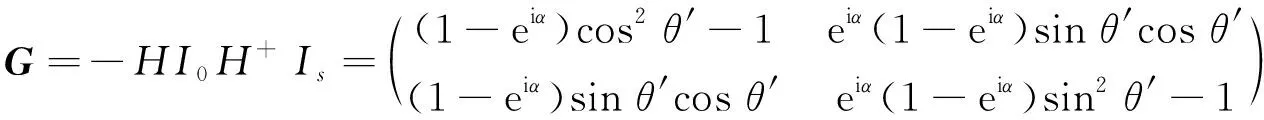
(7)
其中H表示变换算子, 通过量子搜素算法得出数据挖掘的初始数据。将得到的搜索结果记为G=(g1,g2,…,gn)T且在搜索过程中保证搜索的成功概率恒等于1。
2.3 量子神经网络处理
在上述量子搜索中经常要同时搜索多个模式, 会在一定程度上降低量子搜索精度, 因此在量子搜索算法的相位旋转角进行改进的基础上, 利用量子神经网络解决该问题。
量子神经网络中当模拟人的意识时要处理多模式问题, 能有效提升量子搜索精度与速率。量子神经网络结构如图4所示。

图4 量子神经网络结构Fig.4 Structure of quantum neural network
基于上述量子神经网络结构, 将得到的数据搜索结果经过量子比特转换得
|G〉=[|g1〉,|g2〉,…,|gn〉]T
(8)
其中G表示量子比特转换方程。且

(9)
其中gi表示量子网络参数。按照量子网络中的数据参数的更新规则, 对数据参数进行多模式搜索, 得到归一化后的期望输出
G(t+1)=ηΔG(t)
(10)
其中η为量子神经网络的学习更新速率, ΔG(t)为更新梯度值[16]。
利用量子神经网络完成数据归一化处理, 获取数据更新处理结果。
2.4 量子映射变换
经过量子神经网络更新处理完成的数据即为量子算法预处理的结果数据, 然而更新的数据是以量子比特的形式输出, 因此需要通过量子映射变换, 将数据转换为大数据中的正常形式。将量子映射变换过程表示如下
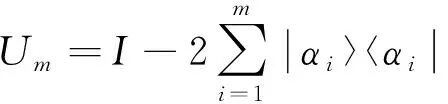
(11)
其中I为量子映射参数,αi为量子基态。根据量子映射变换公式输出增量式大数据预处理结果如下
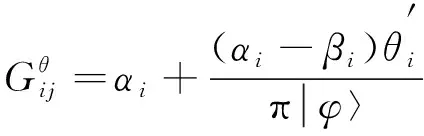
(12)
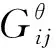
3 数据并行协同过滤
由上述得到的增量式大数据并行挖掘的预处理结果为基础, 利用数据并行协同过滤实现得到数据并行挖掘结果, 其过程为: 计算待挖掘数据之间的相关度, 得到相似度的计算集合, 根据该集合分解大数据的权重矩阵, 得到过滤权重组合, 利用该组合对增量式大数据并行挖掘的预处理结果进行数据并行过滤, 得到增量式大数据并行挖掘的初始结果。首先将所有的大数据的权重构建成为x×y的矩阵[17], 并用向量的形式进行表示, 可表示为R(u=x,y)=(Ru1,Ru2,…,Run)。然后利用相似性计算公式, 求出待挖掘数据之间的相关度, 计算公式如下
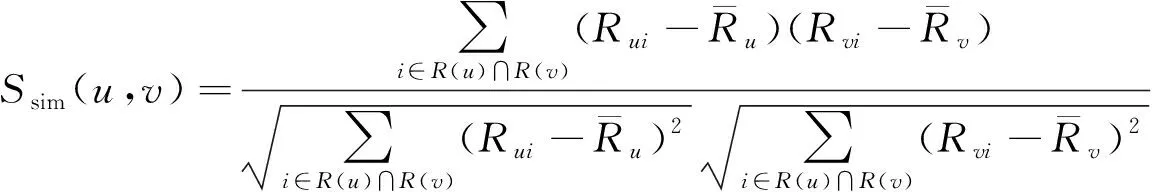
(13)

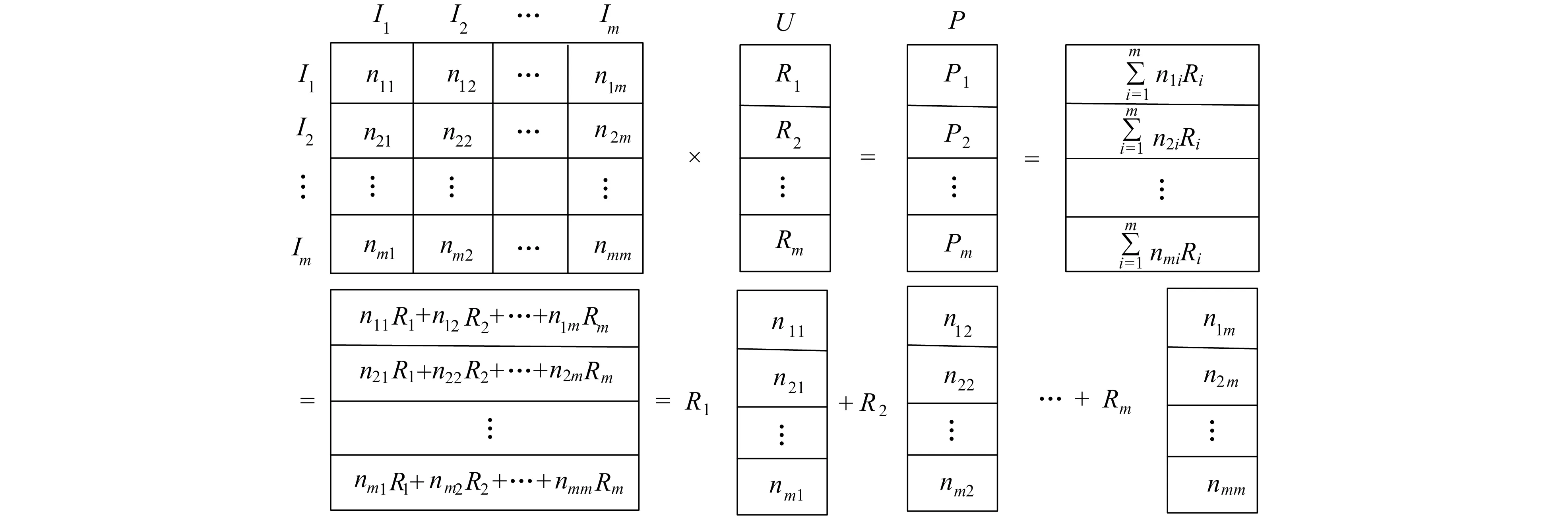
图5 矩阵向量相乘分解图Fig.5 Matrix vector multiplication decomposition diagram
将共现矩阵中项目对应的列向量, 与数据向量中对应的相似度相乘, 即可得到过滤权重组合[19], 最后将各个部分相加即可得到完整的并行协同过滤结果R′, 将并行协同过滤的结果作为静态大数据环境下的数据并行挖掘结果。
4 数据增量式聚类挖掘结果
在静态挖掘结果的基础上, 利用大数据增量式技术与量子算法中的增量性质, 实现对增量式大数据的遍历, 将每次遍历得到的挖掘结果进行模糊聚类, 便可得到增量式大数据并行挖掘结果。应用的增量式技术是指对新增数据, 利用已有结果对其进行处理, 即避免了对已有数据的重新处理, 又可以对新增的数据进行全面处理, 使每次处理的数据量很小, 且使用时间更短, 大幅度提升聚类效果。
在此过程中会出现策略不适用的问题, 为解决该问题, 只需修改因数据变化而涉及的规则即可完成数据的增量式处理。
数据增量式模糊聚类将静态的数据挖掘结果用一个代价函数进行迭代, 聚类原理如图6所示。
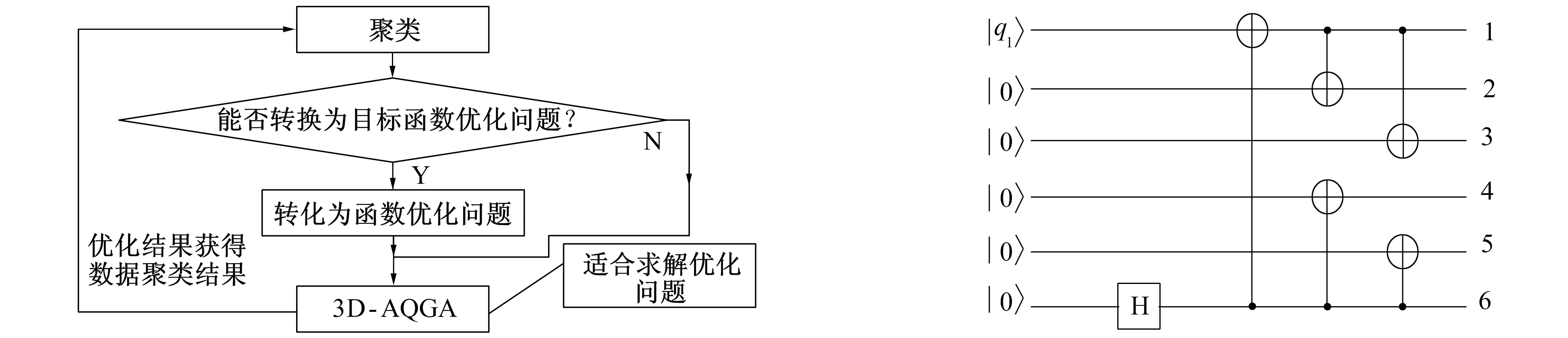
图6 量子模糊聚类原理图 图7 量子编码电路Fig.6 Principle diagram of quantum fuzzy clustering Fig.7 Quantum coding circuit
遵循图中的量子模糊聚类原理, 静态数据挖掘的结果R′分为N个集合数据与k个类别Ci, 定义静态挖掘结果R′中的聚类中心为Pi[20], 且i的取值为[1,k]。根据聚类的类间分离原则, 将增量式聚类结果描述为

(14)
其中Pj表示R′中任意一个数据, 对式(11)进行求解, 便可得出增量式大数据挖掘聚类结果为

(15)
将聚类结果以编码的形式输出便可得到增量式大数据并行挖掘结果, 其中聚类结果的编码电路如图7所示。
第1位比特的态即为单比特逻辑态, 第2~6位量子比特处于态|0〉。在图7中将第6位比特设置控制位, 利用该控制位实现对其他比特位的控制操作, 完成聚类结果的编码, 输出增量式大数据并行挖掘结果。
5 实验结果与分析
5.1 实验环境
由于该实验需要对海量的数据进行处理, 因此对实验环境具有较高的要求。计算机处理器为酷睿i7处理器, 运行存储空间为8 GByte, 内存空间为64 GByte, 并增加外部存储设备为80 TByte。在符合实验要求的设备上安装实验所需的实验方法和对比方法。其中对比方法为不应用量子算法的传统增量式大数据并行挖掘方法。
5.2 实验数据集
为了检测量子算法的增量式大数据并行挖掘方法的综合性能, 进行了实验测试, 选取GroupLens(https:∥grouplens.org/datasets/movielens/)提供的数据集作为实验样本数据。该大数据中包含了不同大小与类型的多个数据集, 挖掘出用户对不同领域的需要具有重要的商业意义。数据集中部分数据描述如表1所示。
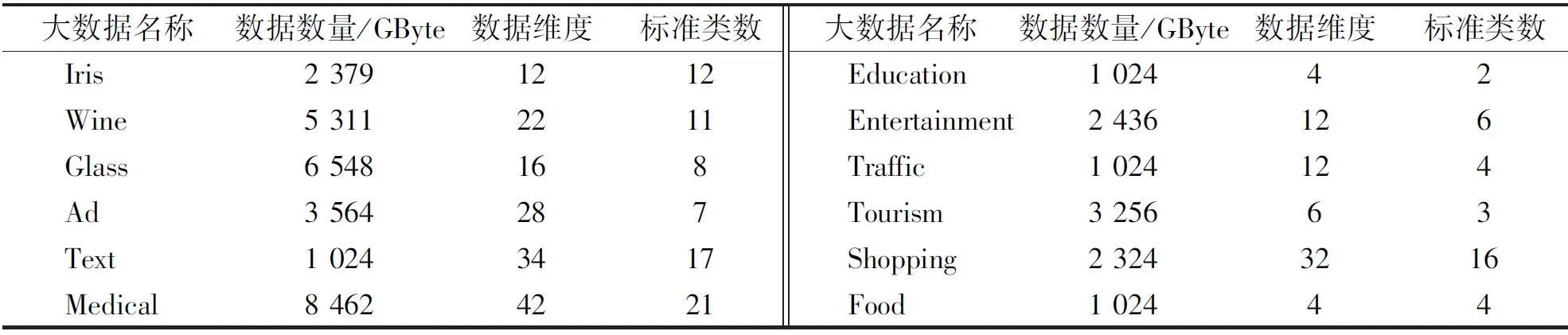
表1 数据集部分数据描述
实验中所用的数据存在的形式为标准格式, 可以直接应用于实验中。
5.3 实验指标
由于文献[8-10]方法都是增量式大数据并行挖掘较新研究, 也是具有代表性的研究成果, 因此选择这3种方法进行实验测试, 实验中选取的主要评价指标如下。
1) 召回率。此次对比实验主要为了检测挖掘方法的性能, 因此选择文献[8]方法与笔者方法进行数据挖掘的召回率对比。召回率的计算公式如下
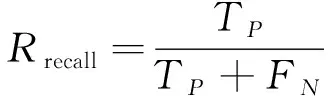
(16)
其中TP表示的是实验数据挖掘的有效结果,FN为数据挖掘的漏报数据结果。因此在实验过程中通过记录实验的有效结果数据与漏报结果数据便可以得出两种数据挖掘方法的召回率。
2) 并行挖掘时间。并行挖掘时间是反应数据挖掘效率高低的重要因素, 因此将笔者方法与3种方法进行并行挖掘时间对比。
3) 并行挖掘准确率。并行挖掘准确率是衡量数据挖掘方法性能的主要因素之一, 因此将笔者方法与3种方法进行并行挖掘准确率对比。
4) 寻优能力。寻优能力是反应并行挖掘结果好坏的主要因素, 将笔者方法与3种方法进行寻优能力对比。在寻优过程中最优迭代次数计算公式如下

(17)
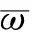
5.4 实验结果
将实验数据按照分类分别输入到两种挖掘方法中, 文献[8]方法与量子算法下的挖掘方法分别按照各自的方法流程对数据进行处理, 最终输出的挖掘结果如表2所示。

表2 实验对比数据
通过表2可以看出, 文献[8]方法的总漏报数据量为2 221 kByte, 而应用笔者方法的总漏报数据量为371 kByte。经过计算可知, 文献[8]方法的平均召回率为83.99%, 而笔者方法的平均召回率为97.25%, 比文献[8]方法高13.26%。
在以下实验中, 选择的大数据类型随机。为了进一步验证笔者方法的优越性, 将3种方法作为实验对比方法进行挖掘时间对比, 结果如表3所示。
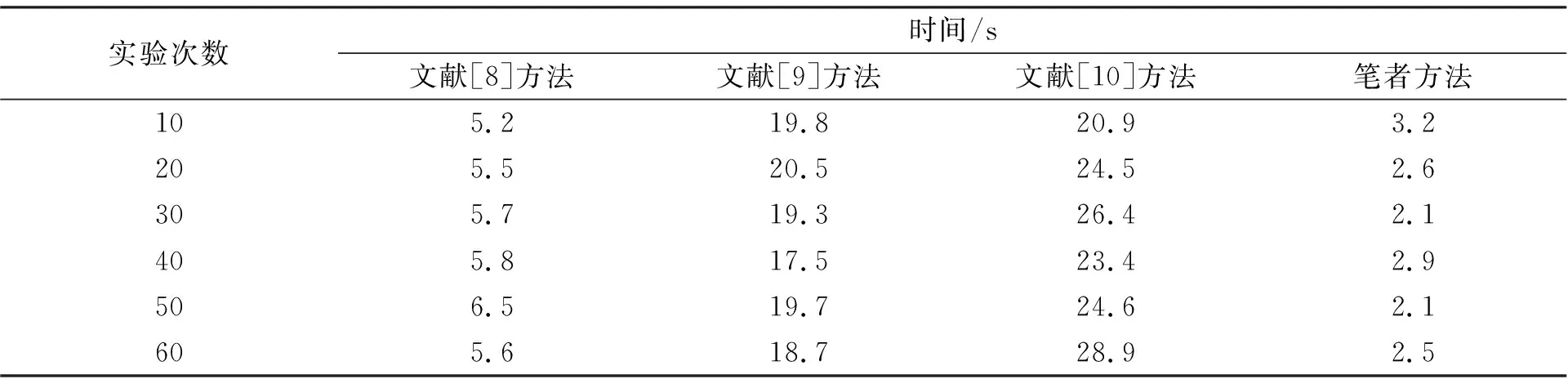
表3 不同方法并行挖掘时间对比
分析表3可知, 文献[8]方法的并行挖掘时间在5.2~6.5 s的范围内变化; 文献[9]在17.5~20.5 s的范围内变动; 文献[10]方法在20.9~28.6 s的范围内变化; 笔者方法在2.1~3.2 s的范围内变动。综合比较4种研究方法的并行挖掘时间, 笔者方法的挖掘时间最短。
在比较不同研究方法召回率与挖掘时间的基础上, 测试不同方法的并行挖掘准确率, 结果如图8所示。
分析图8可知, 文献[8]方法的并行挖掘准确率在60%~70%之间; 文献[9]方法在60%左右, 是4种方法中挖掘准确率最低的; 文献[10]方法在80%~85%之间; 笔者方法在95%以上, 与其他研究方法相比具有较高的并行挖掘精度。
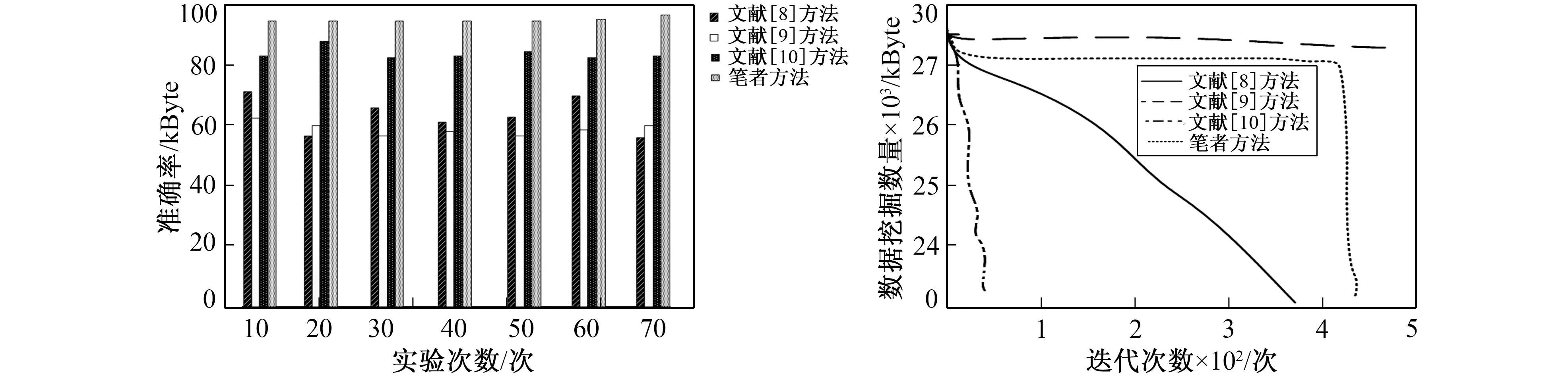
图8 不同方法并行挖掘准确率对比 图9 不同方法寻优能力对比 Fig.8 Comparison of parallel mining Fig.9 Comparison of different methods accuracy of different methods for optimization
在上述实验基础上, 为了更全面比较不同研究方法综合性能, 需要比较不同方法的算法寻优能力, 结果如图9所示。
收敛性主要是指在合适的迭代次数下输出大数据挖掘结果。根据式(17)可知, 在迭代次数为450时数据挖掘结果最优。分析图9可知, 文献[8]方法最快收敛, 其次是文献[10]方法, 而文献[9]方法在500次迭代中一直未收敛, 笔者方法在440左右停止收敛, 因此该方法的收敛性更好。综合比较4种方法可知, 笔者方法的收敛性最好, 寻优能力强, 因此可以得到较好的并行挖掘结果, 有利于挖掘出用户对于不同领域的需要, 表明该方法具有重要的商业意义与应用价值。
6 结 语
随着大数据时代的到来, 数据量正在以惊人的速度增长, 从海量数据中挖掘出有效信息, 有效组织和利用相关数据都是现阶段需要解决的问题。针对传统增量式大数据并行挖掘方法存在的问题, 在增量式大数据并行挖掘方法中应用量子算法, 实验结果表明, 该方法具有较高的召回率, 挖掘时间较短, 挖掘准确率较高并具有较好的算法寻优能力。笔者研究方法不仅提高了数据挖掘的召回率, 同时也大幅提高了时间效率, 为数据挖掘领域的发展及增量式大数据挖掘提供了新思路。
