高中数学函数解题思路多元化的方法
2020-09-01王光灿
王光灿
(福建省宁德市高级中学,福建宁德 352100)
引 言
在当前高中数学教学中,教师应当转变学生的单一解题思维,引导学生探究多元化的解题思路,以充分理解和灵活运用数学函数知识。
一、引导学生应用数形结合思想开展函数问题的分析
教师可以引导学生从数形结合角度,创新学生的函数解题思维,使其将抽象的函数概念转为形象的图形,从而有效地提升高中数学函数解题的效率和质量。
以下面这道高中数学函数题目为例:设奇函数f(x)的定义域为(-∞,0)∪(0,+∞)且在(0,+∞)上单调递增,f(1)=0,则不等式的解集是什么?
分析:在解答这道函数题目时,教师应该引导学生运用数形结合解题思维,结合相关的函数图像来理解函数问题。这样,学生可以有效地找到解题的突破口,以尽快地形成函数解题思路[1]。首先,根据这道函数例题,教师可以提醒学生从题目中的已知条件来找到数形结合的点。比如,从题目“奇函数f(x)的定义域为(-∞,0)∪(0,+∞)且在(0,+∞)上单调递增,f(1)=0”这些描述中,学生可以画出y=f(x)的图像(见图1)。
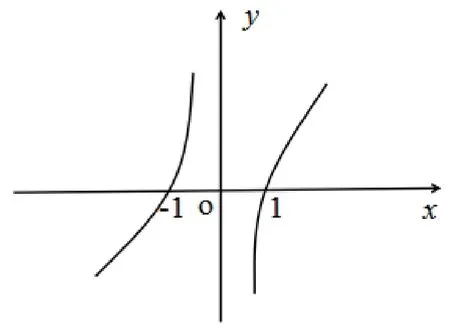
图1
由上述图像可知,当x∈(-1,0)∪(1,+∞)时f(x)>0,当x∈(-∞,-1)∪(0,1)时f(x)<0。然后,学生可以结合具体的函数图像,回归到函数的计算问题。比如,根据题目中的问题,不等式则有最后,学生可以根据具体的不等式,求出不等式的解集。
二、指导学生运用创新的构造解题思路解答数学函数问题
在众多的解题思路中,构造思维方法也是一种很好的数学函数解题思路。它是在原有函数题目基础之下,进行条件或者结论的假设,以利用数学函数题目中的相关信息,构造出满足函数题目所需的条件和结论,促使复杂的函数问题简单化,从而找到函数问题的解答方法[2]。
以下面这道数学函数问题为例:f(x)是定义在R 上的偶函数,当x<0 时,f(x)+xf'(x<0),且f(-4)=0,则不等式xf'(x>0)的解集是 。
分析:从函数题目中,教师可以引导学生观察和寻找其中存在的函数关系。比如,题目中的f(x)+xf'(x<0),出现了“+”的符号,那么教师可以引导学生从构造的思维角度,优先构造出F(x)=xf(x)的函数关系。这样可以将复杂的函数问题简单化。然后,教师引导学生基于这个构造关系,快速利用函数的单调性、奇偶性解答问题。比如,从构造的F(x)=xf(x)出发,继而构造F'(x)=f(x)+xf'(x),那么,当x<0 时,f(x)+xf'(x<0),可以推出F'(x)<0,F(x)在(-∞,0)上是单调递减,又因为f(x)为偶函数,所以F(x)为奇函数。最后,根据f(-4)=0 可得F(-4)=0,则xf'(x>0)的解集应为(-∞,-4)∪(0,4)。教师引导学生利用构造解题思路,可以有效地转化复杂的函数问题,促使学生对题目进行大胆假设,从而找到解题的方法。
三、重视学生的转化思维培养,从划归角度解答函数问题
转化思维也是高中数学的一种重要解题思路。它可以使部分函数问题简单化,同时也有助于学生产生丰富的联想,进而将抽象的函数问题进行一一拆解[3]。比如,当学生拿到一道函数问题时,教师可以先引导学生应用转化思维方法将函数问题简单化;然后利用已经学习过的函数概念研究新函数问题的规律及特点。这有利于降低问题的难度,进而快速地解答出函数问题的答案。
分析:对于这道函数题目,学生可以运用等价转化思维,将函数转化为yx2-ax+y-b=0。然后,令△=a2-4y(y-b)≥0,即4y2-4by-a2≤0,已知题目中的不等式4y2-4by-a2≤0的解集为[-1,4],那么-1 和4 就是关于y的方程4y2-4by-a2的两个根,那么将这两个根代入方程,可以得出a=±4,b=3。在整个解答过程中,这道题目既涉及了函数,又融入了不等式、方程等知识。学生可以运用等价转化的思想,将函数、不等式与方程一步步地转化,从而将复杂的函数问题转化为简单的函数分析,进而求得答案。
四、科学运用分类讨论解题思路进行高中数学函数问题的解答
在解答高中数学函数问题时,学生也可以运用分类讨论思维进行函数问题的解答。学生应该运用如下分类讨论思维进行解题。首先,学生拿到一道函数问题时,必须明确需讨论的对象及取值范围;其次,要正确选择好分类的标准,才能进行分类讨论;再次,针对问题的分类进行逐类讨论;最后,将讨论的结果进行归纳,并进行总结与分析。学生只有严格按照分类讨论的思考步骤,一步步对函数问题进行分类讨论,才能有序、有效地解答出函数问题的答案。
以下面分段函数问题为例:已知函数f(x)=|x-3|+|x+1|,请作出函数f(x)的图像。
分析:对于这道分段函数问题,教师可引导学生尝试利用分类讨论的解题思路,对函数进行分区间讨论。首先,学生需要研究的是已知函数f(x)=|x-3|+|x+1|。其次,学生可以根据x的取值变化,对函数进行分段。比如,当x≤-1时,f(x)=-2x+2; 当-1 <x≤3 时,f(x)=4; 当x>3 时,f(x)=2x-2。最后,学生根据讨论的结果,可以画出相关的函数图像(见图2)。
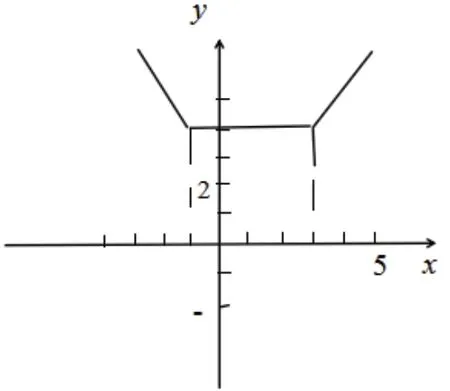
图2
结 语
综上所述,函数是高中数学教学的重要内容。在解答函数题目时,教师应该引导学生从数形结合、构造、转化及分类讨论等多元化的思维角度出发,探究相关函数题目,以从中不断锻炼学生的解题思维,并促使他们掌握这些有效的数学函数解题思维。
