基于ELMAN模型的风电场功率预测研究

董金凤 王亚男

摘要：阐述了风电场功率预测的方法和原理，采用物理方法和ELMAN神经网络相结合的方法，搭建功率预测模型，确定输入参数、隐层单元个数。以某在运风电场为例，利用功率预测模型进行了风电场功率预测。该风电场功率预测模型对风电场功率出力预测具有重要的现实意义。

关键词：物理方法;ELMAN;风电场功率预测模型

0 引言

风电场功率预测系统是根据风电场气象信息有关数据，即数值天气预报，利用物理模拟计算和数学统计方法，结合风电场及机组运行状态，对风电场输出功率进行预测。

应用大气边界层动力学与边界层气象理论，将数值天气预报数据精细化为风电场实际地形、地貌条件下的风电机组轮毂高度處的风速、风向等信息，采用物理方程进行预测的方法称为物理方法。根据历史数据进行统计分析，找出其内在规律并用于预测的方法称为统计方法。综合方法则是物理方法和统计方法相结合的方法，即采用物理方法得到风速、风向等信息，然后采用统计方法找到历史数据的内在规律。

本文采用综合方法，先预测每台风电机组的轮毂高度处的风速、风向等信息，然后采用神经网络找出每台风电机组历史数据的内在规律，预测每台风电机组发电量，然后求和得出风电场全场发电量。

1 风电场功率预测原理

1.1    原理

风电场功率预测系统是根据风电场气象信息有关数据即数值天气预报，利用物理模拟计算和数学统计方法，结合风电场及机组运行状态，对风电场输出功率进行预测，从而满足电力调度部门对风电的调度要求。功率预测系统原理如图1所示。

1.2    神经网络

ELMAN神经网络是ELMAN于1990年首先针对语音处理问题提出来的，是一种典型的局部递归网络。由于ELMAN神经网络在处理序列数据输入输出时具有优越性而得到了广泛应用。基本的ELMAN网络结构如图2所示，主要由输入层、隐层、连接层、输出层组成，是在BP网络的基础上增加了一个“反馈层”，其反馈连接由一组“连接”单元组成，用于记忆隐层过去的状态，并且在下一时刻连同网络输入一起作为隐层单元的输入，相当于状态反馈，这一性质使得部分递归网络具有动态记忆功能，适用于建立时间序列的预测模型。各层的输入均为加权和;隐层的传递函数为某种非线性函数，一般为Sigmoid函数;输出层为线性函数;连接层也为线性函数。ELMAN神经网络的数学模型：

式中，WI1为联系单元与隐层单元的连接权矩阵;WI2为输入单元与隐层单元的连接权矩阵;WI3为隐层单元与输出单元的连接权矩阵;xc（k）和x（k）分别表示联系单元和隐层单元的输出;y（k）表示输出单元的输出;0≤a<1为子连接反馈增益因子。f（x）多取为Sigmoid函数，如公式所示：

2 风电场功率预测模型建模

风电场功率理论上与风速、空气密度线性有关，但在实际发电过程中影响因素众多，例如地形、地貌、尾流、湍流、风机的实际运行状况，这些都不同程度地影响着风电场的实际发电。

本项目采用综合方法，应用大气边界层动力学与边界层气象理论，将数值天气预报数据精细化为在风电场实际地形、地貌条件下的风电机组轮毂高度的风速、风向等信息，根据风电场的测风塔、历史数据找出风速、温度、气压、风向等信息与输出功率间的关系，利用预测的每台风电机组轮毂高度处的风速、温度、气压、风向等，对每台风电机组发电功率进行预测。ELMAN模型的建立过程如图3所示。

2.1    神经网络输入参数的确定

本文利用风电场相邻风机之间的相互关系预测风机功率，即考虑周边风机的影响。风电场风机只有风速测量仪;温度和气压在同一地区变化较小，采用测风塔温度、气压测量数据。选取2号风机和31号风机来比较不同参数组合间的误差。参数组合如下：

2号风机：

组合①：#2风机风速、温度、气压;组合②：#2风机风速和风向、1号风机风速、3号风机风速、温度、气压;

31号风机：

组合①：#31风机风速、温度、气压;组合②：#31风机风速和风向、30号风机风速、32号风机风速、温度、气压。

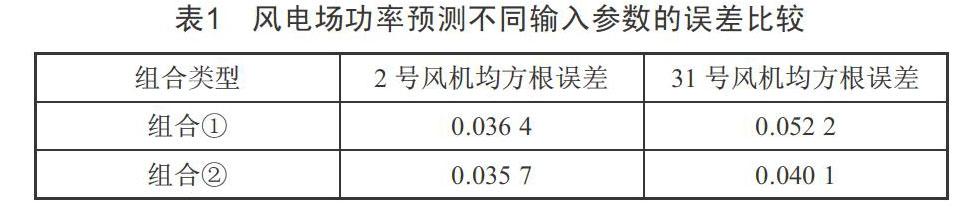
风电场功率预测不同输入参数的误差比较如表1所示。

从表1不同输入参数的误差比较可知，组合②误差更小，准确度更高。因此，风电场采用组合②进行风电场功率预测参数输入。但在实际训练过程中，需要结合地形及风机排布情况，确定风机具体预测参数输入。

2.2    数据整理及归一化

选取风电场一年的原始数据（包括测风塔数据和风电场运行数据），剔除不合理数据，为满足建模需要，需将原始数据进行归一化处理，即归一化值在0～1。

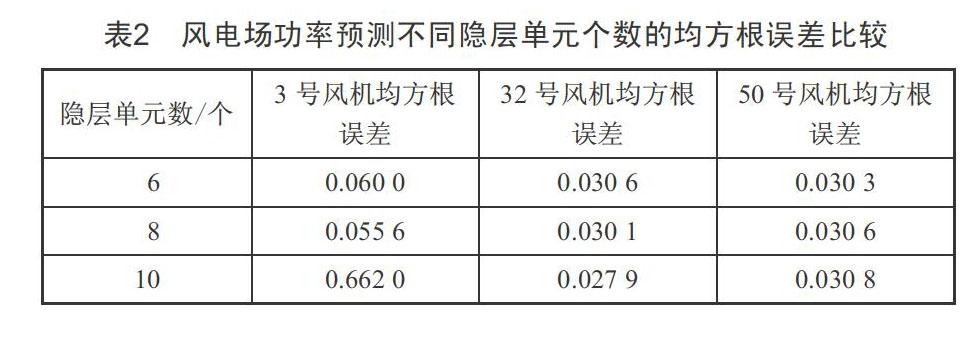
2.3    隐层神经元个数的确定

神经网络隐层神经元个数的确定，对网络的精确度、计算时间等都有很大影响。模型采用不同隐层单元个数分别计算3号、32号、50号风机的输出功率，与实际功率进行均方根误差比较来确定选择隐层单元的个数。表2为3台风机不同隐层单元个数的均方根误差，从表中可以看出，3号风机隐含层单元数为8个时，均方根误差最小;32号风机隐含层单元数为10个时，均方根误差最小;50号风机隐含层单元数为6个时，均方根误差最小。但32号风机、50号风机在不同隐层单元个数下，均方根误差相差不大。因此，在神经网络计算时采用隐层单元数为8个。

3 风电场的功率预测

山东某风电场为丘陵风电场，地形复杂，海拔高度在400～500 m，海拔460 m以上较为平缓，起伏较小。风电场容量49.3 MW，风电机组沿山脊布置。

3.1    数值天气预报

中国气象局为该风电场提供了测风塔及每台风电机组轮毂高度处的风速、风向、温度、气压等信息。风速波动趋势相对一致，但预测风速与实际风速相关性较差，在0.5左右。

3.2    数据整理

选取该风电场每台风电机组一年的原始数据，进行数据整理并归一化处理。

3.3    风电场功率预测

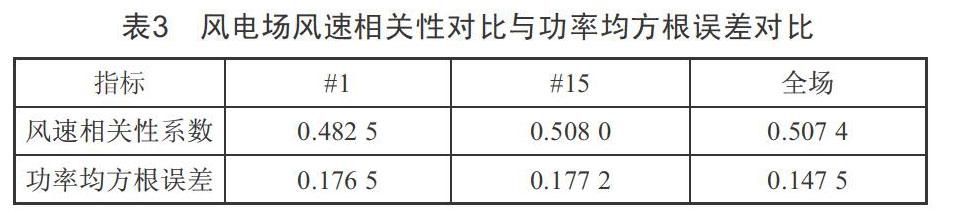
利用Matlab软件建立ELMAN风电机组的功率预测模型，选取每台风电机组一年的归一化数据进行统计分析，找到其内在规律。输入每台风电机组及其周边风电机组的预测数据，对每台风电机组进行短期风电场功率预测。本文选取1号、15号风机进行预测，预测可知，不管全场还是单个风电机组的实际功率与预测功率走向趋于一致，且风速的变化趋势与功率曲线的变化趋势一致，说明在功率预测时，风速预测的准确性是影响风电场功率预测准确性的关键。

在风速相关性较差的情况下，风电场功率预测相对较好，这是因为ELMAN模型本身具有统计分析内部规律的功能。若数值天气预报准确性提高，将大大提高风电场功率预测的准确性。风速相关性对比与功率均方根误差对比如表3所示。

4 结语

本文通过对山东某风电场功率预测结果进行分析，总结了提高预测精度的途径包括以下几个方面：

（1）提高数值天气预报的准确性，风速预测是关键。除用大气边界层动力学与边界层气象理论，将数值天气预报数據精细化到在风电场实际地形、地貌条件下的风电机组轮毂高度处的风速、风向等信息，还需采用风电场测风塔数据作为数值天气预报模型的输入，且需实时更新，以提高数值天气预报的准确性。因此，需确保测风塔数据的完整性和准确性。

（2）加强风电场原始数据的管理。功率预测采用的统计法是基于大量历史数据进行分析的，历史数据的完整性和准确性决定了预测的准确性。可建立数据库，对数据进行挖掘分析，在功率预测时直接调用数据，可提高预测效率。

（3）确保自动化通信连续、可靠。无论是测风塔数据还是历史数据，在功率预测过程需要保证数据连续、完备、可靠。因此，需定期对设备进行检修，实时查看，保证其正常运行。

[参考文献]

[1] 刘震，汪令祥.基于神经网络的风力发电系统风速软测量[J].中国电力，2010，43（11）：87-91.

[2] 谭赟.时间序列分析模型构建与MATLAB实现[J].科技资讯，2009（26）：253-254.

[3] 苏暂，王维庆，王健波，等.风电功率预测准确性分析[J].电气技术，2012（3）：1-5.

[4] 朱晟，蒋传文，侯志俭.基于气象负荷因子的ELMAN神经网络短期负荷预测[J].电力系统及其自动化学报，2005（1）：23-26.

收稿日期：2020-06-08

作者简介：董金凤（1982—），女，山东人，工程师，主要从事新能源方面工作。