基于改进AHP的装备试验鉴定条件变量评估

叶康 曹裕华 钱昭勇

摘要：针对装备试验鉴定过程中条件变量评估的问题，本文分析了传统方法中存在的不足，介绍了改进层次分析法（Analytic Hierarchy Process，AHP）的基本思想和步骤，并基于该方法对X型坦克作战试验中的条件变量进行评估，确定了主要条件变量。经实践证明，改进的AHP能科学高效的对各类条件变量实施评估，能为装备试验鉴定的设计与实施提供参考，值得进一步推广与应用。

Abstract： In view of the problem of condition variable evaluation in test evaluation， this paper analyzes the shortcomings of the traditional method， introduces the basic idea and steps of the improved Analytic Hierarchy Process （AHP）， evaluates the condition variable in the battle test of X-type tank based on the method， and determines the main condition variable. It has been proved by practice that the improved AHP can scientifically and efficiently evaluate various condition variables， and can provide a reference for the design and implementation of test evaluation， which is worthy of further promotion and application.

關键词：AHP 试验鉴定;条件变量;评估

Key words： Analytic Hierarchy Process test evaluation;condition variables;evaluation

中图分类号：TJ0                                         文献标识码：A                                  文章编号：1006-4311（2020）23-0240-04

0  引言

随着装备试验鉴定改革工作的深入推进，传统试验鉴定模式面临巨大调整，同时急需新的理论方法来指导新体制下装备试验鉴定的具体设计与实施。装备试验鉴定的本质就是测试装备在不同变量条件下的各项参数性能，因此确定主要条件变量是开展装备试验鉴定的第一步，也是试验设计的核心任务之一。

条件变量是影响试验结果的变量，是试验中考察的因素[1]。它们从装备的使用背景中提炼而来，涉及到装备的性能试验、作战试验和在役考核试验阶段，以不同角度影响着装备的各项性能指标和试验任务完成情况。理想状态下应对所有条件变量进行考察，这样试验内容最完善，试验结论最能反映装备的真实水平。但由于试验条件的约束，只能通过综合评估，选取相对重要的条件变量进行详细考察，对其余的则进行简单的控制与记录。

条件变量数目众多，关系模糊复杂，无法用定量的标准直接衡量其主次关系。为科学合理的评估各类条件变量，许多学者开展了相关研究。吴溪，郭广生，王亮等人认为可采取专家法对试验变量条件进行赋值，由此评估其权重大小[2]。董莉萍通过专家问卷打分法对29个影响装备全寿命费用的因素进行调查，最后将各专家的结果进行聚合，得到评估结果[3]。李康宁在satty提出的九标度法基础上，运用层次分析法分析各类试验条件变量的重要性，并以此为依据选出试验过程中的条件变量[4]。相较于专家法而言，层次分析法虽然过程复杂，但是评价角度更全面，受评价者主观影响因素较少，更符合试验鉴定工作的高要求。本文结合试验鉴定工作实际，提出采取改进的层次分析法对装备试验鉴定过程中的条件变量进行评估，为今后装备试验鉴定的设计与实施提供参考。

1  层次分析法的改进

1.1 层次分析法的基本思想

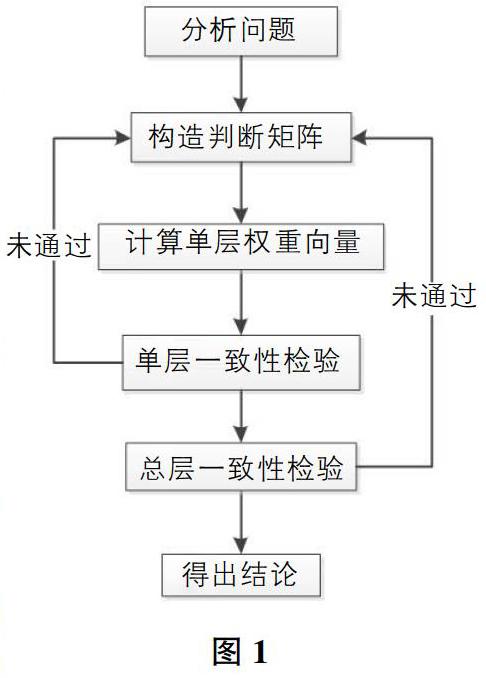
层次分析法是一种将定性分析与定量分析相结合的多准则决策的系统分析方法[5]。首先通过分析待解决问题，构建出对应的层次结构模型，其中包括目标层、准则层及方案层;然后采取九标度法对其中因素逐层两两定性比较并赋值，形成判断矩阵;最后根据判断矩阵的特征向量确定下层因素对上层因素的权重大小，从而推算出方案层对目标层权重大小排序。其过程如图1所示。

1.2 层次分析法的不足与改进

层次分析法将各因素间的对比结果分为“相同重要”“稍微重要”“明显重要”“强烈重要”“极端重要”等九个等级，采取九标度法对其进行赋值，如有多名专家参与评估，则将结果进行算术平均处理。这种方法存在三点不足：一是评价标准模糊，相邻评价标准间的差异难以把握，难以做出准确判断;二是计算量大，生成的判断矩阵往往一致性较差，需要反复修正;三是数据处理不够严谨，没有根据专家的个体差异分析其评估数据价值的高低并进行精确处理。针对以上问题，可以从三个方面进行修改：一是将传统的九标度法改为三标度法，使评价标准更加明确，减少评价过程中的不确定性，降低计算难度;二是通过最优传递矩阵对传统判断矩阵进行一致性转化，避免了后期的一致性检验，减少了解决问题的工作量[6];三是基于群决策理论，对每名参评专家进行评价打分，确定各组评估数据的可信度，并采取加权平均法改造原有判断矩阵。

1.3 基于改进层次分析法的评估步骤

①构建层次结构模型。依据问题背景，分析待解决问题，确定评价目标、评判标准以及待评价方案，并找到其内部关联，形成目标因素、准则因素和方案因素，由此构建对应的层次结构模型。

②建立判断矩阵群。从第二层开始，以上层某元素为依据对该层的相关元素进行两两定性对比，并根据三标度法（0，1，2）赋值，将生成比较矩阵进行一致性转化，构建判断矩阵群。设层次结构模型某层有n个因素a1，a2，a3…an专家针对该层上层某元素生成的比较矩阵记为A，A=（aij）n×n，其中aij表示ai比aj的重要等级，aij的取值标准为：

则一致性矩阵C为该层对上层某元素的判断矩阵。所有判断矩阵的集合称为该层次结构模型的判断矩阵群，记为D。

③基于群决策理论改造判断矩阵群。设有m个专家参加测评，根据他们的个人信息，从从业年限、職称等级、学历、积极性对其进行赋分，赋分标准如表1所示。

④计算权重值。

因为第二步已经将判断矩阵做了一致性转化，所以此时的权重向量W不用进行一致性检验。

随后依据层次结构模型，合并同层次的判断矩阵权重向量，组成准则层对目标层的单排序相对权重向量及方案层对准则层的权重矩阵，记为H1和H2，方案层对目标层的合成权重向量记为H，则有：

H=H1H2（7）

由此得出各方案因素对目标层因素的权重大小。

向量H内的各个数值就分别对应着每个方案层因素相对于目标层因素的权重大小。

2  基于改进AHP的X型坦克作战试验条件变量评估

现对陆军X型坦克开展作战试验，该坦克主要编配于装甲旅，机步旅及山地作战部队，用于遂行东南山岳丛林、西北高原高寒山地、中部城市平原及其他地方的快速部署、机动突击、地域管控等作战任务，摧毁敌装甲车辆、野战工事、后勤库所，消灭其有生力量，亦可执行反恐维稳及国际维和等任务。其作战试验的条件变量取自于真实作战需求，且一般在多种因素叠加状况下开展试验。根据该坦克的服役环境和使用范围，确定影响其作战效能和作战适用性的条件变量，可以归纳为自然因素和人为因素两大类。其中自然因素包括地形、天气、天时、海拔、气温;人为因素包括火力威胁、电磁威胁、生化威胁、辐射威胁、作战模式。由于条件限制，现要求选出五个主要条件变量进行分析观察，对其他变量则用适当方法予以控制和记录。

2.1 构建模型

装备作战试验设计是一项复杂的系统工程[7-9]，它既要达到充分检验被试装备作战效能和作战适用性的目的，同时又受到现有试验条件的约束，因此在选取主要条件变量的过程中，需统筹好试验条件变量本身的战术意义以及试验条件的关系，确保在有限的试验条件下创造最大的试验效益。其中战术意义需从影响概率、影响程度、影响时长三个方面评判;试验条件需从物资经费、时间精力、技术手段、装备损耗、重叠比率五个方面考虑。各准则因素的含义如下：

2.1.1 战术意义

影响概率：X型坦克受该条件变量的影响的时间占作战任务总时间的比率。

影响程度：在单位时间内，该条件变量对X型坦克对应作战效能和作战适用性提升或降低的程度。

影响时长：在执行作战任务过程中，该条件变量单次出现并影响X型坦克的平均时间长度。

2.1.2 试验条件

物资经费：为调控并观测该条件变量所需消耗的物资和经费成本。

时间精力：为调控并观测该条件变量所需消耗的时间和人力成本。

技术手段：依托现有技术手段对该条件变量实施调控和观测的可行性。

装备损耗：在该条件变量作用下的作战试验过程中，装备损坏和消耗的程度。

重叠比率：在该条件变量下的作战试验科目，与前一阶段作战试验及性能试验的试验科目的重叠程度。

综合上文中的条件变量及评价因素，结合层次分析法原理，构建层次分析模型如图2所示。

2.2 构建判断矩阵群

为保证评估的准确性，参评专家的数量应大于准则层因素的数量[10]。因此选取十名专家参与X型坦克作战试验条件变量的评估工作。从层次结构模型的第二层开始，以该型坦克的作战试验要求为依据，采取三标度法两两对比，构建比较矩阵。其中准则层一对目标层需构建一个比较矩阵，记为A1;准则层二对准则层一中的“战术意义”和“试验条件”需构建两个比较矩阵，分别记为A2，A3;方案层对准则层二中的“影响概率”“影响程度”“影响时长”“物资经费”“时间精力”“技术手段”“装备损耗”“重叠比率”需要构建八个比较矩阵，分别记为A4，A5，A6，A7，A8，A9，A10，A11。然后再通过公式（1）（2）将上述比较矩阵进行一致性转化，得到的判断矩阵。以准则层二对“试验条件”构建判断矩阵的过程为例：

以此类推，分别求出11个对应的判断矩阵，其集合记为判断矩阵群D。由于篇幅限制，就不一一列出。

2.3 改造判断矩阵群

参评专家的基本信息如表2所示。

根据表1的赋分标准，得到每名专家的得分情况，并根据公式（3）算出其对应的权重系数，结果如表3所示。

根据公式（4），将每名专家的权重系数与该专家打分得到的判断矩阵群相乘并求和，即得到改造后的判断矩阵群。

2.4 计算权重值

对改造后的判断矩阵群，根据公式（5）（6）求出每个判断矩阵对应的权重向量：

根据计算结果，将各条件变量按权重大小排序，如表4所示。

2.5 结果分析

在综合考虑影响概率、影响程度、影响时长等八项评估准则的基础上，结合（通过）改进AHP，确定电磁威胁、作战模式、地形、天气和火力威胁为X型坦克作战试验中的主要条件变量。根据计算数据，还可得知“影响程度”占据了评估因素中42.4%的权重，是“时间精力”的十八倍之多，是确定主要条件变量最看重的评估因素，战术意义类评估因素占据了63.79%的权重，说明在在选取X型坦克主要条件变量时，应把战术意义作为主要评估标准，把试验条件的作为辅助评价标准;另外，如果存在某条件变量战术意义评分较高，但是由于试验条件评分较低而落选，则应该考虑采取其他方式对该条件变量进行补充考察，例如模拟仿真等。

3  结束语

本文运用改进的AHP，对X型坦克的作战试验条件变量进行了评估，通过构建层次分析模型，建立判断矩阵，改造判断矩阵，计算条件变量权重，最终确定选择方案。该方法不仅能综合考虑条件变量本身的战术意义及试验任务的实际条件，还能通过改进措施，进一步降低评价的模糊性，簡化一致性检验步骤，提升数据聚合的合理性，使评估标准更加清晰，评估过程更加高效，评估结论更加可信。改进的AHP适用于各种结构复杂、定量数据缺乏下的条件变量评估工作，能对主要条件变量的选取提供决策依据，为模拟仿真等其他试验途径的必要性提供数据支撑，对装备试验鉴定的设计与实施具有重要意义，值得进一步推广与应用。

参考文献：

[1]曹裕华.装备试验设计与评估[M].北京：国防工业出版社，2016.

[2]吴溪，郭广生，王亮，高振辉.装备作战试验科目设计方法研究[J].火力与指挥控制，2018，43（11）：177-183，188.

[3]董莉萍.基于FAHP的装备全寿命费用风险评价研究[D].哈尔滨工程大学，2015.

[4]李康宁. 一体化试验优化设计方法研究[D].哈尔滨工业大学，2016.

[5]Saaty T L. A scaling method for priorities in hierarchical structures[J].Journal of mathematical psychology， 1977，15（3）：234-281.

[6]陈烈，陈星明，韩方建.改进AHP在采矿方法优选中的应用[J].化工矿物与加工，2019，48（07）：1-5，8.

[7]吴溪，穆歌，李大勇，高振辉.武器装备作战试验设计原理[J].兵器装备工程学报，2019，40（01）：24-27.

[8]秦金柱，廖兴禾.装备作战试验设计过程分析[J].装甲兵工程学院学报，2018，32（04）：12-15.

[9]黄一斌，郭英.装备作战试验基本问题初探[J].军事运筹与系统工程，2017，31（04）：69-74.

[10]盛宝.改进的AHP在产能建设评价中的应用[J].云南化工，2018，45（02）：157.