命题逻辑联结词完全性证明
——数学归纳法的应用
2020-08-31曹发生
曹发生
(贵州民族大学民族文化逻辑与认知研究中心,贵州 贵阳 550025)
1 两种数学归纳法的比较
第一,数学归纳法的步骤。
(1)基础步骤当n=1时,这个命题为真。(2)归纳步骤假设当n=k时,这个命题为真,那么当n=k+1时,这个命题也为真。
第二,数学归纳法的步骤。
(1)基础步骤当n=1时,这个命题为真。(2)归纳步骤假设当n=1,…,k时,这个命题为真,那么当n=k+1时,这个命题也为真。
数学归纳法的两个步骤缺一不可。前一步骤是基础,后一步骤是核心。归纳步骤中要能表明由前一步得到后一步,环环相扣,以至对每一个自然数都能成立。
将第一数学归纳法基础步骤中的“当n=1时,这个命题为真”,推广为“当n=1时,这个命题为真;当n=2时,这个命题都为真”。此时归纳步骤中假设当n=k时,这个命题都为真,来证明当n=k+1时,这个命题也为真。
这就是我们对第一数学归纳法的推广。下文将说明在有些时候这个推广是必要的。
第一,数学归纳法基础步骤中的“当n=1时,这个命题为真”是要证明的,归纳步骤中假设当n=k时,这个命题也为真,来证明当n=k+1时,这个命题也为真。而第二数学归纳法基础步骤中的“当n=1时,这个命题为真”是要证明的。归纳步骤中假设当n=2,…,k时,这个命题都为真,来证明当n=k+1时,这个命题也为真。
它们之间的区别在于第一数学归纳法假设步骤中仅仅是“假设当n=k时,这个命题为真”。而第二数学归纳法假设步骤中是“假设当n=2,…,k时,这个命题都为真”。
2 命题逻辑联结词的完全性证明
联结词组是完全的定义为:这组联结词能够定义其他所有的逻辑联结词[5]。
命题集合的归纳定义方式[5],基础部分:原子命题属于命题集合;归纳部分:假设属于命题集合,则属于命题集合。
下面先利用推广后的第一数学归纳法对联结词函数的元的个数进行归纳证明。
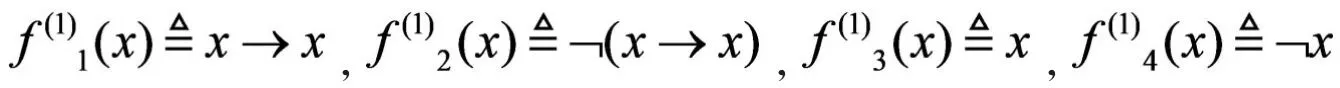
下面再利用第二数学归纳法对联结词函数的元的个数进行归纳证明。

注:用第二数学归纳法的归纳步骤中含有“假设当n=2,…,k时,这个命题都为真”,而“当n=2时,这个命题都为真”就是假设有的条件,这与上面的推广的第一数学归纳法不同,那里是直接证明“当n=2时,这个命题为真”。所以我们对第一数学归纳法中基础步骤的推广是有意义的,因为用第一数学归纳法又没有要求证明“当n=2时,这个命题为真”,而在证明归纳步骤时候又需要“当n=2时,这个命题为真”。
数学归纳法可以证明与自然数n有关的命题,可是要证明的命题有时候很难联想到与自然数n有关。要证明当n=2时命题为真时,利用其前一步“当n=1时,这个命题为真”没办法证得,于是可以在数学归纳法的基础步骤中增加当n=2时命题成立具体的证明;本文对命题逻辑联结词的完全性用推广的第一数学归纳法和第二数学归纳法两种方法给出证明。
