加密货币价格溢出效应的DCC-GARCH模型

曾 莹，曾柳畅

(湖北工业大学理学院，湖北 武汉 430068)

对于金融资产收益率序列波动过程的分析，国内外已经有不少学者对此做出了研究。例如构建广义自回归条件异方差模型(GARCH)克服了自回归条件异方差模型(ARCH)使用高阶滞后项描述资产收益率序列波动过程的缺点，但却又无法衡量资产间可能存在的相互作用关系，因此Engle(2002)提出了动态条件相关广义自回归条件异方差模型(DCC-GARCH)，该模型的条件相关系数矩阵随时间变化而变化，可以研究金融时间序列之间的时变相关性[1]。在此基础上，国外学者利用DCC-GARCH模型对不同金融市场之间的动态关联性和溢出效应进行分析。如Jose(2019)利用DCC-GARCH模型分析亚太地区各国外汇市场间的溢出效应[2]。

关于加密货币投资风险的研究，Victor (2019)等利用GARCH和GAS模型对比特币的风险收益进行建模，认为比特币在投资策略中具有重要意义[3]。而以Schiller(2017)为代表的经济学家认为加密货币的投资存在明显的泡沫[4]。总之，国外学者对加密货币投资风险的研究结论分为两种：一种认为将加密货币作为多样化投资的选择可以对冲风险，提高投资的风险收益；另一种认为加密货币的投资风险将导致巨大的损失。

相对于国外学者，国内学者更多从理论上对加密货币的风险进行研究。谢平(2015)、邹传伟(2018)和惠志斌(2018)分别对加密货币的特点、经济学问题和潜在的投资风险进行分析[5-7]。黄跃(2017)对比分析了加密货币与传统金融工具的差异，提出加密货币的投资风险[8]；吴桐(2019)对加密货币项目 Libra 进行分析，认为其存在增大系统性金融风险的可能[9]。但上述文献的不足主要在于：一是将加密货币市场作为一个独立的市场进行分析，并未对加密货币与其他金融资产之间的联动性进行分析；二是只从理论上对加密货币可能存在的风险进行讨论，并未对加密货币与其他金融市场之间是否存在溢出效应进行实证分析。

DCC-GARCH模型已广泛应用于不同金融市场间的动态关联和溢出效应研究。基于上述研究，通过构建DCC-GARCH模型，对加密货币市场与传统金融市场之间的动态关联性和溢出效应进行研究。

1 模型和数据

1.1 模型设定

与传统金融市场一样，加密货币收益率序列呈现出波动率聚集、尖峰厚尾等金融时间序列特征，运用GARCH类模型可以较好地对序列进行拟合分析。因此，采用DCC-GARCH模型对加密货币市场与传统金融市场之间的动态关系进行分析，反映市场之间的溢出效应。

DCC-GARCH模型由美国经济学家Engle提出。该模型可以捕捉不同市场之间的动态关联性和溢出效应。模型的估计分为两步。首先对单变量收益率序列建立GARCH模型并获得标准化残差，其次对标准残差建模估计相关矩阵，得到动态条件相关系数。

假设金融资产收益率序列rt均值为0，服从以下分布：

rt|Ft-1～N(0,Ht)

参数ωi，αi，βi满足

ωi>0，αi，βi>0，αi+βi<1

1.2 数据选取和处理

笔者研究加密货币与传统金融资产的联动性和溢出效应，选取加密货币价格和股票投资、黄金、大宗商品和货币资产四大类7个市场指数的收盘价格日数据作为研究样本。由于加密货币的种类多达上千种，选取Bitcoin、Ethereum、Ripple、Litecoin和USDT等5种加密货币作为加密货币市场的代表，其市场份额稳定在82%。股票投资类资产选择S&P500、NASDAQ、NYSE和VIX。货币资产指标选择美元指数。对应的时间区间为2015年8月7日至2019年12月13日，数据频度为日度。数据来源包括雅虎金融(https://finance.yahoo.com)、英为财情(https://cn.investing.com)。表1归纳了实证分析所使用的数据集合及来源。

表1 数据集合及数据来源

由于不同市场之间存在不同的交易日期，通过剔除市场之间不重叠的交易日交易数据，共得到1097个时序样本。对所选取的5种加密货币的收益率序列，以各加密货币所占市场份额为权重，计算5种加密货币收益率的加权平均值作为加密货币市场的收益率序列。为保证所研究的时间序列的平稳性，对收盘价格进行对数收益率化处理，将资产价格序列转化为收益率序列，即rt=lnpt-lnpt-1。运用R3.3.3对数据进行处理和分析。

1.3 数据的描述性分析

收益率序列的描述性统计结果如表2所示。加密货币收益率序列的均值为0.00245，超过其他四类传统金融资产的投资收益率，而高投资收益率往往伴随着较高的投资风险。除了波动率指数之外，加密货币收益率序列的标准差和最大收益率均大于其他传统资产，最小收益率也低于其他类型的传统金融资产，说明加密货币收益率的波动大于传统金融资产收益率的波动。对于普通投资者而言，收益率完全体现了资产的投资机会，且与投资规模无关。加密货币收益率的高波动性表明了加密货币的投资风险大于传统金融资产的投资风险，这可能与加密货币价值的形成机制相关。不同于主权货币来源于政府背书的价值，加密货币的价值由参与者的共识确定，在信息不对称的条件下容易滋生价格操纵的行为，使得加密货币的投资收益率呈现较高的波动。而收益率序列的偏度不为零，除了NYSE和USDX外，峰度K>3，在1%的置信水平下，收益率序列不服从正态分布。这表明收益率序列之间具有相似的基本特征，都呈现出尖峰厚尾、偏态分布的现象。

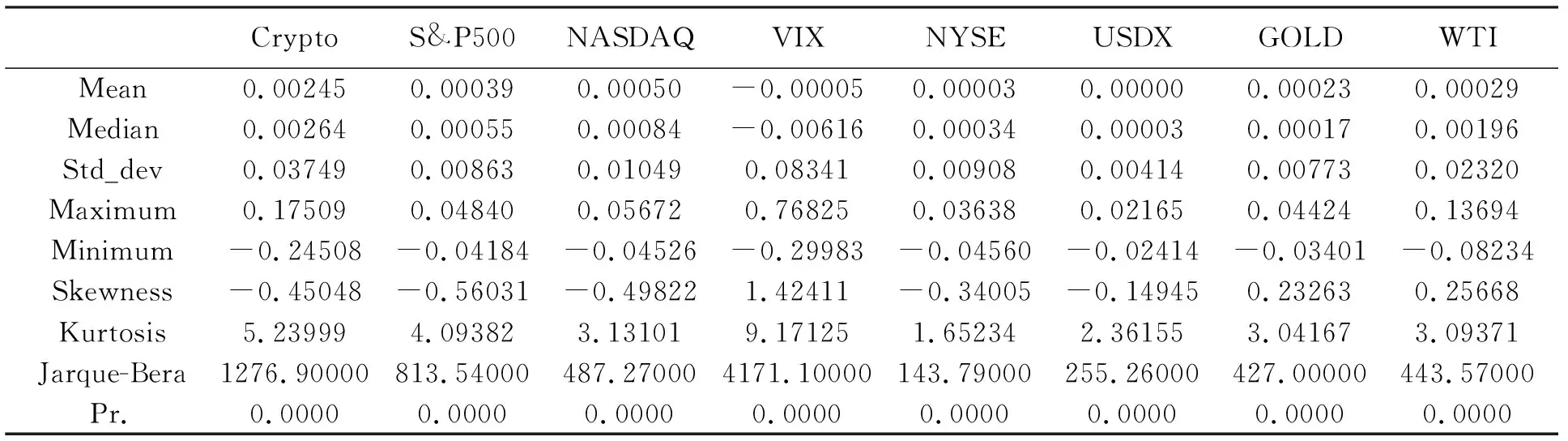
表2 变量描述性统计

2 实证分析

2.1 平稳性与ARCH效应检验

在拟合DCC-GARCH模型前，需要对数据进行平稳性检验和条件异方差效应检验。检验结果如表3所示。通过对各收益率序列进行单位根检验和ARCH效应检验发现，在5%显著性水平下，所有收益率序列都通过了单位根检验和ARCH效应检验，说明收益率序列平稳，存在条件异方差性，可通过建立DCC-GARCH模型进行分析。

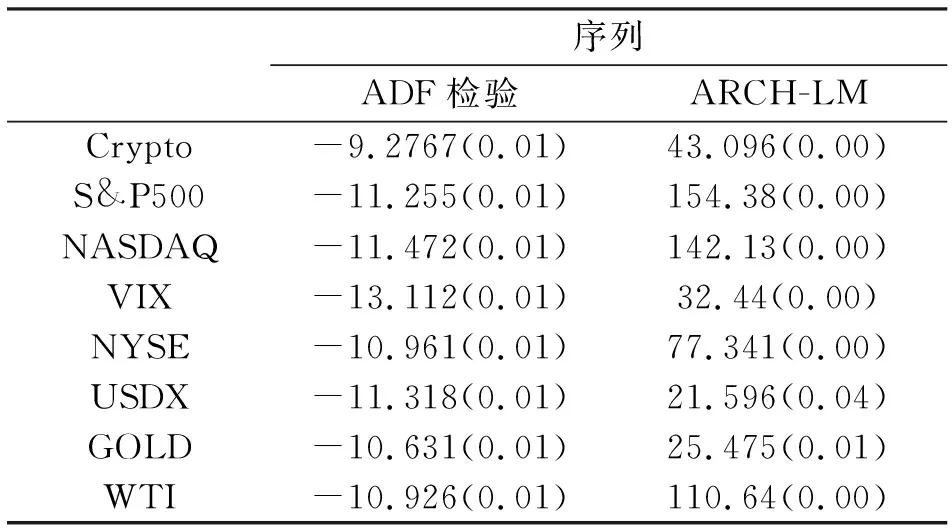
表3 平稳性、ARCH效应检验

2.2 DCC-GARCH(1,1)模型建立

通过单位根检验和ARCH效应检验之后，对收益率序列建立DCC-GARCH模型，分析各收益率序列之间的动态关联性以及溢出效应。

根据DCC-GARCH模型的原理，第一步建立单变量GARCH模型。以加密货币收益率序列和S&P500收益率序列为例。图1为加密货币和S&P500平方收益率序列的样本PACF。虽然收益率rt序列存在少许序列相关性，但主要特征还是rt2的PACF显示强烈的线性相关性。对收益率序列拟合单变量GARCH模型，模型估计结果如表4所示。两个收益率序列拟合的模型的ARCH(α)和GARCH(β)在1%显著性水平下均通过了检验，对拟合模型的标准化残差平方序列进行检验：

Q(15)c=9.262659(0.86)

Q(15)S&P=14.58406(0.48)

式中，括号内数值对应检验统计量的P值。

这说明拟合的模型能够充分描述波动率序列的相依关系。

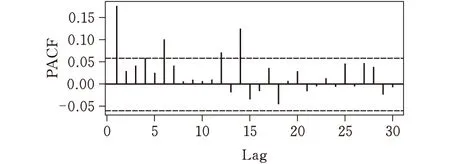
(a)加密货币

(b)标普500图 1 加密货币和标普500平方收益率序列PACF图

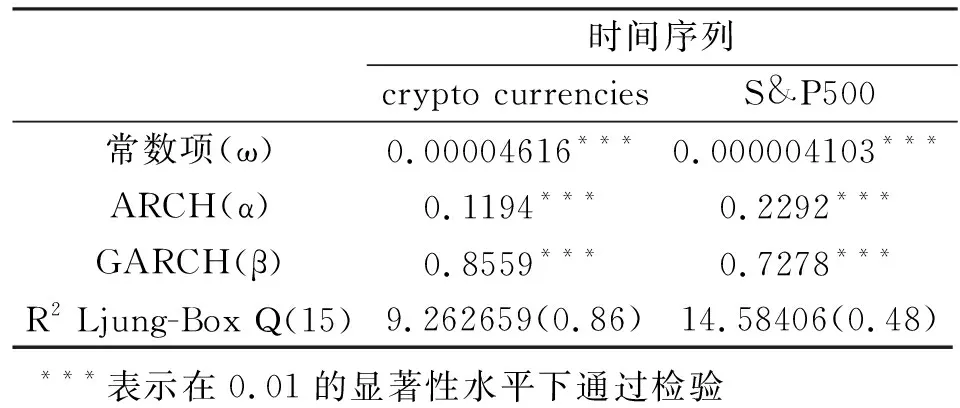
表4 GARCH(1,1)估计结果

第二步是建立动态条件相关(DCC)模型。在第一步的基础上，估计DCC模型的系数，估计结果如表5所示。DCC模型的系数α+β<1，说明模型回归结果稳健，加密货币与标普500收益率序列之间的动态条件相关性具有持续性。

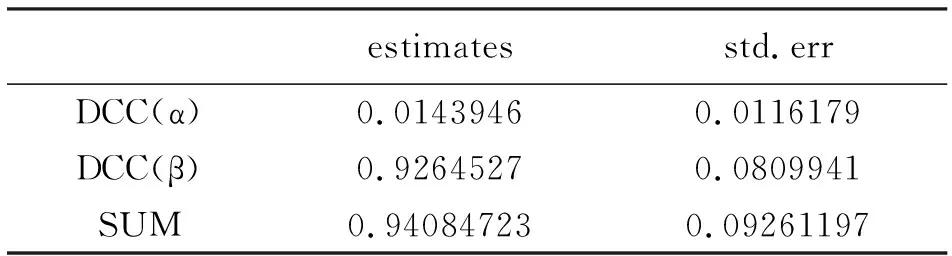
表5 DCC模型估计结果

表6为加密货币与传统金融资产GARCH(1,1)模型估计结果。表7为加密货币与传统金融资产DCC模型的估计结果。通过对所有金融资产收益率序列建立单变量GARCH模型发现，除了美元指数的常数项不显著之外，其余参数均在不同的显著性水平下通过检验，标准化残差平方序列的LB检验表明拟合的模型均能充分描述波动率序列的相依关系。DCC模型拟合结果表明，模型参数均满足α +β <1，模型回归稳健，加密货币与传统资产收益率序列之间的动态条件相关性具有持续性。

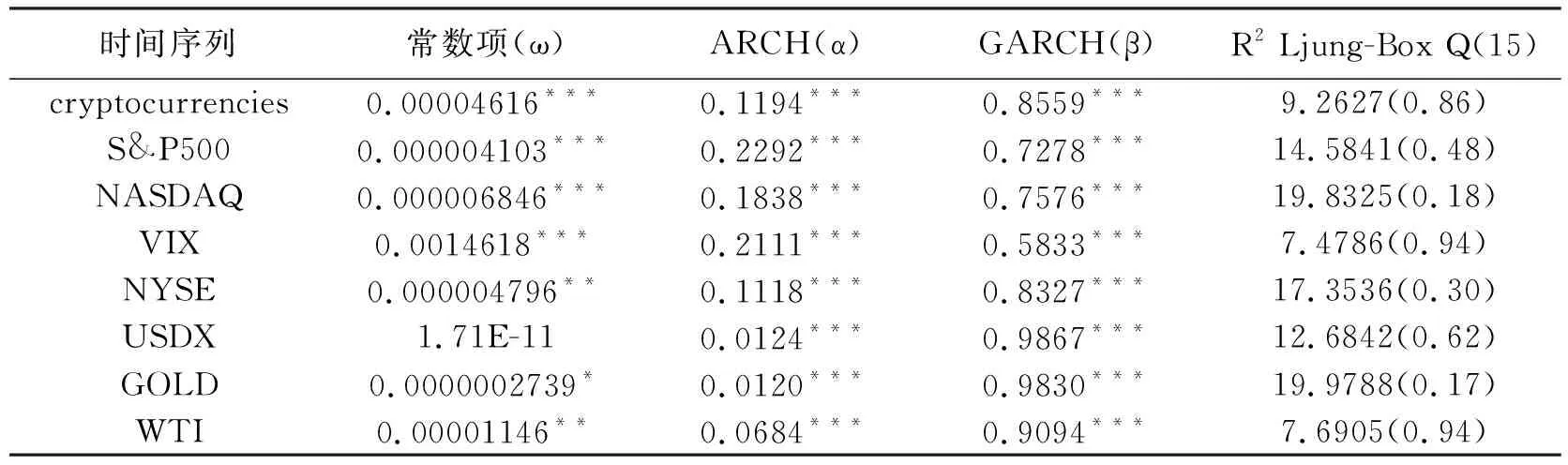
表6 加密货币与传统资产GARCH(1,1)模型估计结果

表7 加密货币与传统资产DCC模型估计结果

2.2 动态关系分析

通过建立合理的DCC-GARCH(1,1)模型，得到各收益率序列之间的动态条件相关系数，进一步对动态条件相关系数进行描述性统计分析并绘制时序图。结合表8、图2和图3，加密货币市场与传统金融市场之间的相关性存在时变特征，且与不同市场的相关强度不同。加密货币市场与传统金融市场之间动态相关系数的波动范围在-0.2～0.2之间，均值较小，与传统金融市场的联动性较弱。其中，加密货币市场与黄金和S&P500之间的联动性最强。加密货币与WTI、NYSE和VIX之间的动态相关系数出现在多个时间点上为负的情况，表明加密货币与大宗商品市场和股票市场之间的动态关系出现了一定程度的分割，不同市场之间较强的分割性形成对加密货币市场溢出效应的影响。

表8 DCC-GARCH(1,1)模型动态相关系数统计表

图2 加密货币与股票市场动态相关系数时序

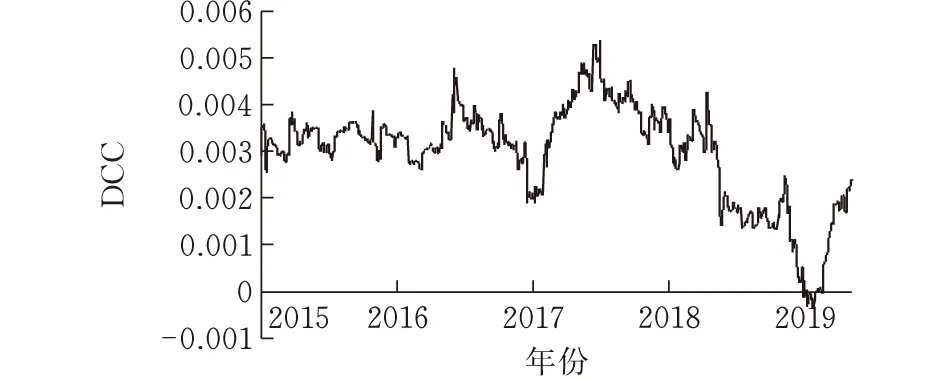
(a)加密货币与美元指数动态条件相关系数

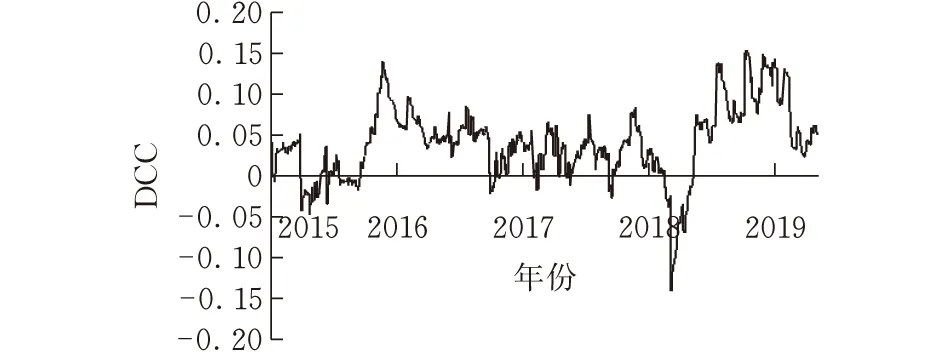
(b)加密货币与黄金价格动态条件相关系数

(c)加密货币与石油价格动态条件相关系数

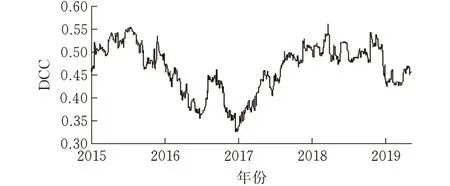
(d)石油价格与纽约证券交易所指数动态条件相关系数图 3 加密货币与其他主要金融市场动态相关系数时序

从DCC-GARCH(1,1)模型的回归结果看，系数α>0，β>0且接近于1，说明加密货币市场与传统金融市场之间存在正向溢出效应。加密货币价格出现剧烈波动时，会通过汇率等多种途径对传统金融市场造成影响。但由于加密货币市场与传统金融市场的融合处于初级阶段，时变相关系数也表明两者间的相关关系较弱，存在溢出效应但影响较低。以大宗商品市场和股票市场为例对传统金融市场联动性进行分析，均值为0.46，市场趋势相同，联动性高，说明传统金融市场之间存在显著的溢出效应。

从现实来看，加密货币从出现时便由于与其他资产类别缺乏强相关关系而被作为一种对冲传统市场风险的新资产类别。作为一种新的数字资产，加密货币与传统资产的相关性较弱，这是由于加密货币市场与传统金融市场的增长因素不同。后者受到经济增长和利率等多方面的影响，而前者的影响因素更多的是来自于不同国家的监管以及投资者的信心。与传统市场的低相关性，可以让投资者在进行金融投资时实现多样化投资，在经济增速减缓或金融危机的背景下，投资者通过在加密货币市场分散投资，可以降低风险。作为一个新兴市场，加密货币市场与传统金融市场之间的分割影响了市场间价格波动的信息传递，市场之间的信息传递效率较低，其对传统金融市场的作用仍有局限性。

3 结论与建议

采用2015年8月7日至2019年12月13的加密货币与四类金融资产时间序列数据，通过构建DCC-GARCH(1,1)模型，实证分析了加密货币市场与传统金融市场之间的动态关系和溢出效应。结果显示：加密货币收益率波动与传统金融资产收益率波动一样存在尖峰厚尾和波动聚集特征，且加密货币的投资收益率及波动程度超过传统金融投资资产收益率。作为一个新兴市场，加密货币市场存在一定的无效性和波动性。虽然去中心化的特点使加密货币不通过金融机构进行交易，导致监管不完善，并且加密货币投资存在投机行为和较高的投资风险，但也不能否认其作为金融投资工具的可能。相对于传统金融市场之间存在的强关联性，加密货币市场与传统金融市场之间的动态关联性较弱，具有一定的溢出效应。但由于还处于与金融市场融合的初级阶段，其影响程度较低，这表明加密货币市场与传统金融市场之间存在体制差异和分割现象。由于存在法律上的限制和投资者偏好等因素的影响，投资者资金无法在不同市场之间实现无成本转移。

综上所述，提出以下建议：

1)政府针对加密货币市场风险来源制定相关政策以增强加密货币市场的有效性。通过政策引导加密货币融入现有金融体系，明确可交易的加密货币种类和应用场景，提高平台的合规经营水平。加密货币交易平台应在政策的引导下加强自律自查，作为信息中介实现有序经营。由于加密货币市场起步较晚，与传统金融市场的弱相关性可以增强分散投资的效果，因此在制定政策时需要考虑政策的溢出效应以及由其引起的反馈效应，通过健全监管体制、强化风险控制、破除体制机制隔离，实现市场相互连通，使加密货币成为数字经济创新的重要组成部分。

2)投资者在进行投资前应充分了解投资的风险性和交易机制。在加密货币市场上进行交易的加密货币多达上千种，投资者需选择正规的加密货币种类和交易平台规避自身的投资风险。由于加密货币收益率存在波动聚集的现象，投资者在进行投资时需分析加密货币整体市场及目标加密货币的未来趋势，掌握市场节奏，综合自己的资金规模和投资偏好等选择正确的投资周期进行投资。