基于组合模型的黑土区土壤有机质含量预测分析

卢牧原，刘 源，刘桂建，*

(1.合肥工业大学 资源与环境工程学院，安徽 合肥 230009； 2.中国科学技术大学 地球和空间科学学院，安徽 合肥 230026)

土壤有机质泛指土壤中来源于生命的物质，是组成土壤固相部分的重要成分。一般条件下，土壤有机质含量在一定范围内与土壤肥力呈正相关，因此土壤有机质含量也被视为评价土壤肥力的重要指标[1-2]。快速、准确地测定土壤有机质含量对于了解土壤肥力、提高作物产量，以及智慧农业的实施等均具有重要意义。传统的土壤有机质测定方法耗时长、工作量大，难以满足快速无损的土壤有机质含量测定需求[3]。现阶段，光谱分析、遥感解译、GIS空间分析技术等已在耕地质量和农业信息监测中得到了一定的应用，尤其是遥感数据具有覆盖范围广、实时性和现势性强等优点，为迅速而准确地获取土壤质量评价指标提供了有利条件。

目前，国内外有关土壤有机质的预测研究主要是基于多光谱、高光谱数据展开，通过对光谱数据进行处理筛选出最佳波段及其组合从而构建多种预测模型来提高有机质空间预测的精度[4-6]。已有的研究表明，通过对光谱数据进行数学变换处理，最大化波段所包含的信息量，能够有效地降低波段间信息冗余，增强其与研究目标间的相关性，从而筛选出最佳波段用于提高预测模型的精度。章志等[7]利用基于信息量的最佳指数法(OIF)从陆地成像仪(OLI)影像多波段数据中筛选了最佳波段组合用于地类提取；郑丽等[8]计算了SPOT(地球观测系统)波段数据间的协方差，利用最佳因子和雪氏熵法选取了最佳波段和不同颜色通道，可较全面地反映各类地物差别；徐明星等[9]应用偏最小二乘回归(PLSR)模型对光谱原始数据和经数学变换处理后的数据进行建模分析，发现不同土壤有机质预测最佳光谱指标与成陆年代相关。以上研究说明，利用光谱数据可以筛选出适用于土壤有机质空间预测的最佳波段。前人在最佳波段选取的研究中多采用信息量算法，较少利用波段贡献率来选取最佳波段，且较少对传统非线性回归方法与不同机器学习方法进行对比研究。

本研究基于陆地卫星8(Landsat8)影像波段，进行不同数学变换来突出影像数据中的光谱信息，同时利用标准化模型量化经数学变换的光谱数据贡献率，结合相关性分析筛选出最佳波段用于建立土壤有机质预测模型，探讨典型黑土区土壤的有机质含量预测波段及其模型优选问题[10-12]。

1 材料与方法

1.1 研究区概况

研究区位于海拉尔地区某农牧场，系黑龙江额尔古纳河水系，地处内蒙古自治区东北部，呼伦贝尔中部偏西南，地理坐标介于119°30′48″～120°35′36″E、49°5′44″～49°27′15″N。研究区东部地势起伏较大，整体高程处于600～800 m，土壤种类主要包括黑钙土、草甸土和少量沼泽土，属于典型黑土区[13]。研究区属中温带半干旱大陆性草原气候，受大兴安岭的屏障作用，气候特点为夏季降水集中、冬季严寒漫长，地面积雪时间长，年平均降水量为350～370 mm。

1.2 土壤数据

研究区长8.2 km，宽15.6 km，面积约77 km2。测区表层土为40～50 cm的黑色腐殖质层，更深处为钙积层，pH值为7.0～7.8。土壤有机质含量来源于农场测土配方数据，共选取135个样点，采样时间为2018年4月6—9日，随机取其中70%样本用于建模，其余30%样本用于验证。研究区土壤样点分布如图1所示。样本集具体信息如表1所示。

由图2可知，样本集中有机质含量分布连续性较好，但不完全符合随机分布，因此仅满足偏态分布。考虑到有机质含量分布受地形、年前种植作物、施肥的影响，因此预测模型对样本是否符合正态分布无需求。训练集与检验集样本的分布较均匀(表1)，基本覆盖整个研究区域，且变异系数均大于16%(属于中等变异，说明样本较为离散)，因此认为该样本集适于建模。从空间位置和数学变换上进行分析，本研究采用的训练集和检验集具有合理性和代表性。

1.3 影像数据

本次研究采用的一景影像数据是来源于USGS(美国地质调查局，United States Geological Survey)的Landsat8卫星影像，多光谱影像分辨率为30 m，云量为3.13%，全色影像分辨率15 m，热外红影像分辨率100 m。所选影像时间为2018-04-08，与样本采集时间接近，且地表裸露无降雪或冰冻现象，适于土壤有机质含量预测研究[14]。

影像的预处理过程简述如下：为了将图像的像元值(DN值)转换为绝对辐射亮度，并消除大气分子和气溶胶散射的影响，运用ENVI 5.X软件对图像多光谱波段分别进行辐射定标和大气校正。为避免由传感器、成像时间等带来的图像差异，以10 m分辨率的天地图影像(影像时间为2019-07-04)为基准，对影像进行几何校正，均方根值(RMS)低于0.5个像元。最后，利用研究区边界感兴趣区对影像进行裁剪。

1.4 建模方法

本研究采用PLSR结合反向传播神经网络(BPNN)、支持向量机(SVM)方法建立土壤有机质含量光谱预测模型，旨在为典型黑土区土壤有机质含量预测找到更为合理的模型。

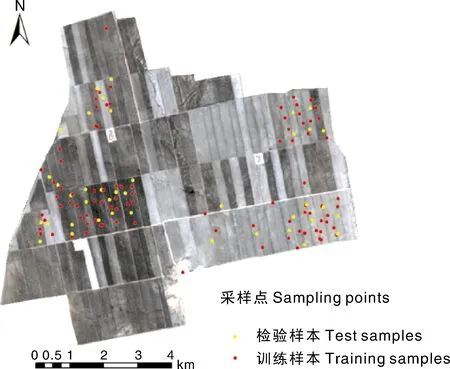
图1 采样点分布Fig.1 Distribution of sampling points

1.4.1 PLSR标准化模型构建

PLSR在各自变量内部高度线性相关且为多因变量对多自变量时效果最好，是一种新型的多元统计数据分析方法，在样本量较小时表现较好[15-16]。PLSR在考虑自变量矩阵的基础上增加了响应矩阵，能够降低噪声的干扰，降低数据维度，因此具有一定的预测能力。但如自变量的单位存在差异，则各自变量前的系数将无法标识该因素的重要程度；因此须通过标准化处理，将各自变量(包括因变量)都转化为标准分，再进行线性回归，此时得到的回归系数即可反映对应自变量的重要程度，此时的回归方程即为标准回归方程[17]。

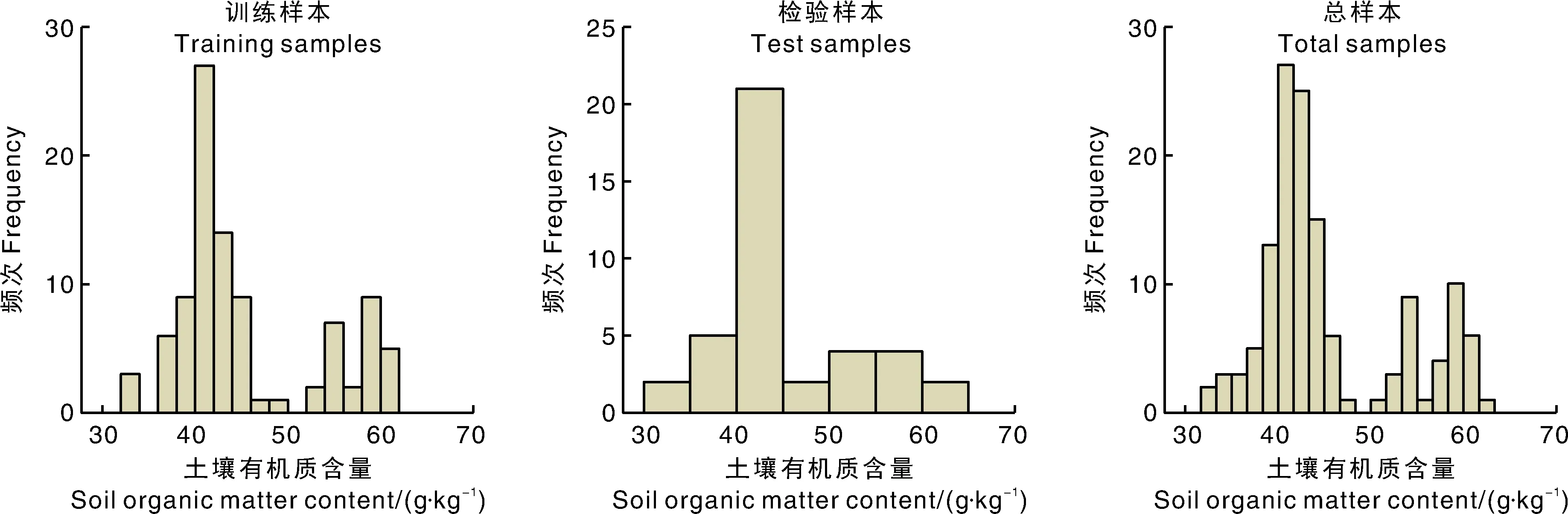
图2 样本集土壤有机质含量分布直方图Fig.2 Histogram of soil organic matter content distribution in sample set

表1 样本集有机质含量统计

由于执行标准分转化是对原始变量作投影处理，得到各自变量对因变量的贡献率；因此，标准回归方程两边都取0时，常数项也取0[18]。

1.4.2 BPNN模型构建

BPNN模型又称连接机模型，是一种具有强大非线性逼近能力与容错能力的多层前馈网络[18-20]。反向传播意为模型在进行模拟的过程中能够收集网络系统所产生的误差，将误差反馈到神经元从而调整权重的分配[21]，这样就得到了可以拟合出原始输出值的人工神经网络系统。

本文基于Matlab软件实现BPNN模型的构建，并采用自适应lr动量梯度下降法作为训练函数[22]。训练次数设定为500，观察准确度变化进行调整；mini-batch参数的值在2n内选择，一般n不大于8；隐含层和输出层传递函数分别选用非线性Tansing函数和线性purelin函数；其余参数的选择可以依据样本情况反复多次试验确定。

1.4.3 SVM模型

SVM方法建立在统计学习理论和结构风险最小原理基础之上，根据有限的样本信息在模型的学习精度和无差识别样本的能力之间寻求最佳折衷，以期获得最好的泛化能力[23]。传统回归方法当且仅当回归函数值f(x)完全等于因变量y时才认为是预测正确，计算其损失；而SVM认为|f(x)-y|>α参数的loss函数偏离程度不大即可。本研究中SVM的实现基于LibSVM运算库，该程序的核心参数是对核函数的设定。一般处理多元回归问题时，核函数选择径向基函数(RBF)，但值得注意的是核参数g(gamma)和惩罚参数c(cost)的设定。g是RBF核函数参数，表征RBF核函数宽度，默认变化范围[2-8，28]；c是RBF惩罚参数，用于平衡经验风险和模型复杂度，默认变化范围是[2-8，28][24-25]。

1.5 图像处理方法

为了增强反射率与研究对象之间的相关性，对反射率进行多种数学变换以有效削弱噪声。本研究通过ENVI 5.X软件的bandmath和IDL编程对预处理后的反射率实现4种数学变换处理，并以此为变换指标。将预处理简记为L。

1.5.1 一阶微分(L′)

图像微分梯度计算是对图像边缘的提取。对于离散图像来说，一阶、二阶微分处理可作为锐化空间滤波器，使用领域的微分作为算子，增大邻域间像素的差值，使图像的突变部分变得更加明显，以增强图像的突变信息、图像的细节和边缘信息。

1.5.2 二阶微分(L″)

图像的二阶微分采用的Laplace算子对噪声敏感，在恒定区域二阶微分值为0，在灰度台阶或斜坡的起点处微分值不为0。因此，二阶微分算法在检测某像素是在边缘亮的一侧还是暗的一侧时，可利用“零跨越”确定边缘的位置，得到的图像边缘较细。

1.5.3 倒数对数(LR)

通过对光谱进行对数变换，将图像的低DN值部分扩展、高DN值部分压缩，以达到强调图像低DN值部分的作用[26]。倒数变换能够将新值转换为同一量级的数据，使之具备更好的对比性。

1.5.4 主成分分析(PCA)

主成分分析是一种常用的数据分析方法，通过线性变换将原始数据变换为一组各维度线性无关的变量，通过数据压缩消除冗余和数据噪音，提升数据处理速度[27-28]。PCA的工作就是从原始的空间中顺序地找一组相互正交的坐标轴，新的坐标轴的选择与数据本身是密切相关的。事实上，这相当于只保留包含绝大部分方差的维度特征，而忽略包含方差几乎为0的特征维度，从而实现对数据特征的降维处理。

1.6 模型精度评价

对于预测模型来说，最重要的是能对新出现的数据样本进行准确预测。一般来说，为避免由于模型总是倾向于更好地拟合训练数据从而出现过拟合现象[29-33]，多通过决定系数(R2)、均方根误差(RMSE)、相对分析误差(RPD)对模型精度进行预测。RMSE可用来衡量观测值同真值之间的偏差[34]。一般来说，R2越大、RMSE越小，说明模型的精度越高。而对于RPD来说，当RPD>1.8时，可认为其预测能力较好，当RPD>2.0时，可认为其预测能力极好。

2 结果与分析

2.1 标准化模型建立与特征波段优选

为进一步定量化分析土壤有机质与光谱的关系，避免信息冗余，通过构建PLSR标准化模型对预处理后和经数学变换处理后的波段数据集建立标准回归方程，从经过不同处理后的波段集中选取最具有特征性、相关性最高的波段作为建模因子。在Matlab软件中利用PLSR标准化模型对各波段集进行回归建模，结果如表2所示。经过不同处理后的波段对应的标准系数越大，说明该波段对模型的贡献越大。以波段贡献率为主要依据，并结合相关性进行最佳特征波段的选取。同时，为避免信息冗余，当挑选最佳特征波段时，应避免选择同一对应波段。可以看出：预处理后的数据和经LR处理后的波段集中第10、11波段的贡献率较高；经PCA处理后，第5、6、8波段贡献率较高；经一阶微分处理后，第8波段的贡献率较高；经二阶微分处理后，第3、7波段贡献率较高。

各波段反射率与有机质含量的相关性如表3所示，综合考量挑选相关性达显著水平(P<0.05)、贡献率较高的波段构建PLSR标准化模型。最终选取预处理后的第10波段，PCA处理后的第5、6、8波段，二阶微分后的第7波段，以及LR处理后的第10波段这6个波段作为建模波段。

2.2 模型对比分析

2.2.1 PLSR模型

以经过标准分筛选的6个组合波段反射率为自变量、土壤有机质含量为因变量，建立相应的PLSR预测模型。由图3、表4可知，训练集的R2为0.62、RMSE为4.59 g·kg-1，检验集的R2为0.59、RMSE为5.03 g·kg-1、RPD为1.72。由R2大于0.6可知，模型效果较显著，能够对土壤有机质含量进行较准确的估算。但是整体精度不高(RPD<1.8)，预测过程存在着随机性。

2.2.2 BPNN模型

以经过标准分筛选的6个组合波段反射率为自变量、土壤有机质含量为因变量，建立具有3层结构的BPNN模型。隐含层节点设定为15，隐含层函数设定为双曲正切S型函数Tansig，输出层函数为线性函数Logsig。如表4所示，相较于PLSR模型，BPNN模型在检验集上的R2、RPD增大，RMSE减小，表明其效果优于PLSR模型，说明BPNN能较好地应对非线性预测问题。但是，该模型的运算过程相对不稳定，依赖于参数调整和环境配置。结合先验经验对波段进行优选，可提高精度，并减少可能出现的过拟合问题。

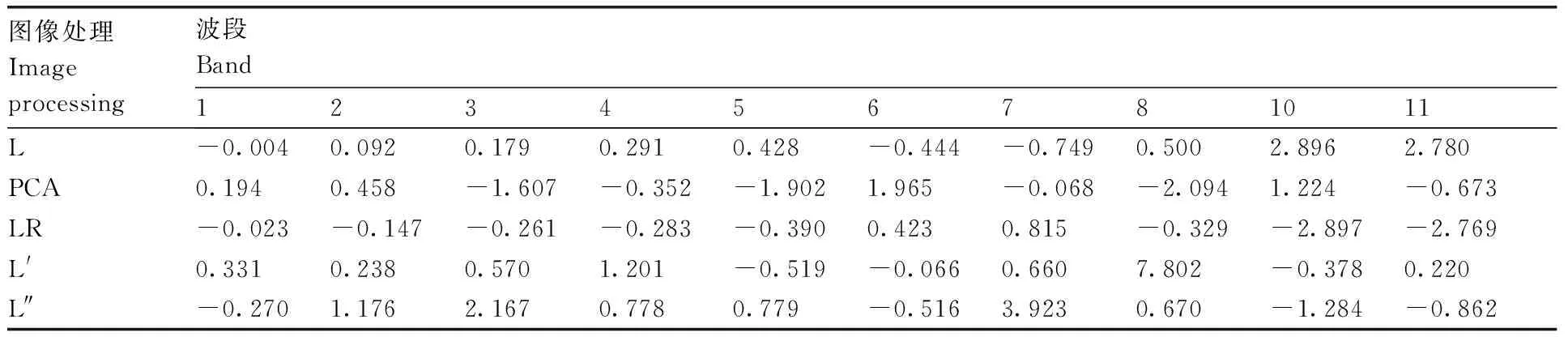
表2 基于PLSR标准化模型的各波段对应标准系数

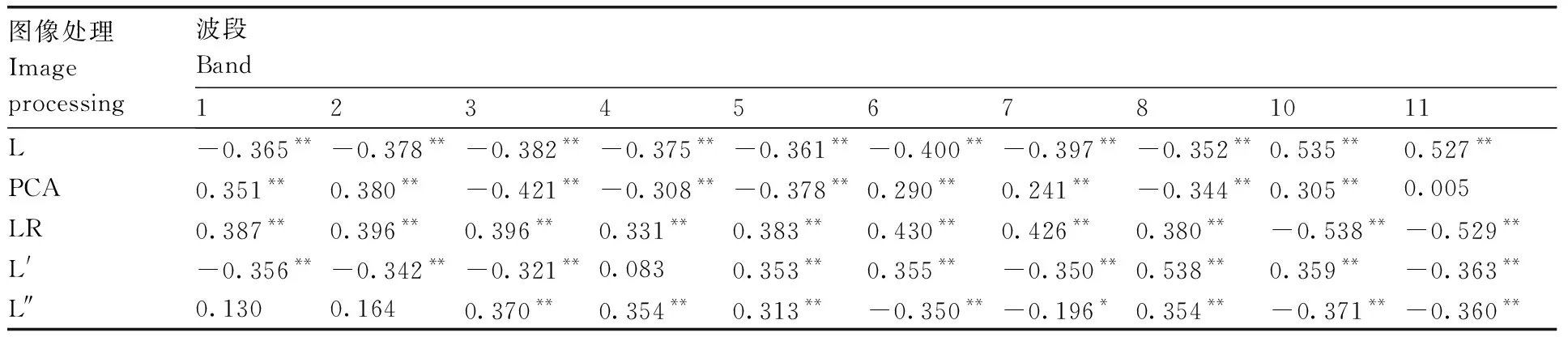
表3 有机质含量与各波段反射率和变换形式的相关性

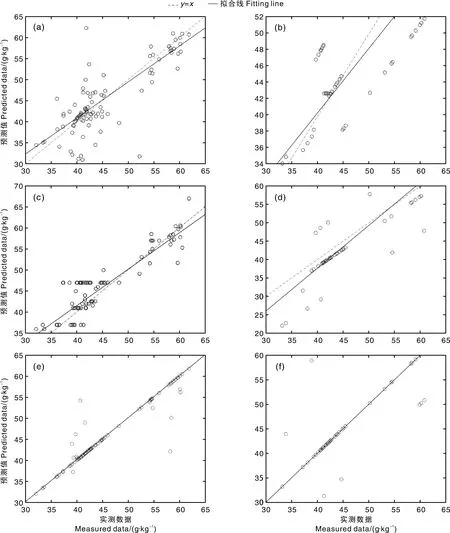
图3 PLSR(a、b)、BPNN(c、d)、SVM(e、f)模型在训练集(a、c、e)和检验集(b、d、f)上的土壤有机质含量预测值与实测值Fig.3 Predicted and measured data of soil organic matter content in training set (a， c， e) and test set (b， d， f) based on PLSR model (a， b)， BPNN model (c， d)， and SVM model (e， f)， respectively

2.2.3 SVM模型

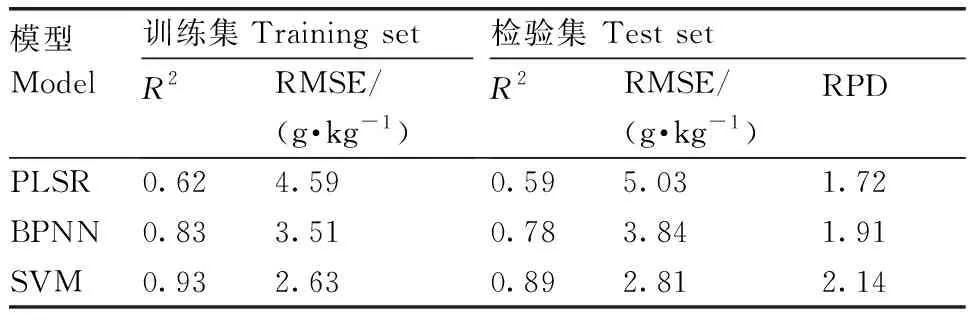
表4 不同模型的土壤有机质含量建模精度

基于LibSVM运算库，以土壤有机质含量为拟合目标，经过模型设定和优选，最终确定SVM类型为v-SVR，径向基函数为核函数，并对各参数进行调整，构建出SVM模型。如表4所示，SVM模型在检验集上的R2、RMSE、RPD分别为0.89、2.81 g·kg-1、2.14，说明该模型能够对土壤有机质含量进行较准确的预测，总体效果在构建的3种模型中最优。

综合对比3种建模方法，SVM模型与BPNN模型的拟合效果较好，说明本研究中机器学习方法在土壤有机质含量预测的建模效果上优于传统统计方法[35]。但机器学习方法对于建模环境和参数调整的要求较高，隐含层建模过程复杂，仅能通过多次试验确定适宜当前环境的最优方法，并须通过多次测试避免过拟合。在本研究中，SVM建模方法效果最佳，这种在高维特征空间中使用线性函数假设空间的新型机器学习方法避免了波段间的信息重叠，因此，建模质量好，且运算量小。

2.3 有机质含量分布预测

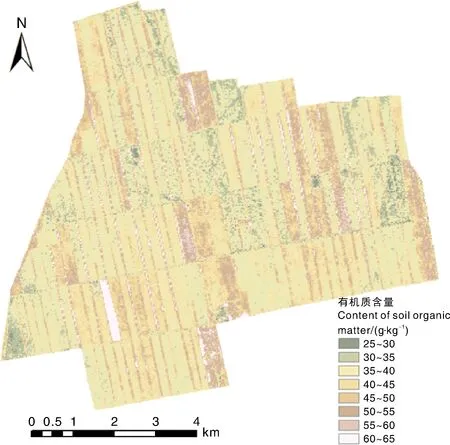
图4 研究区有机质含量分布预测结果Fig.4 Prediction of soil organic matter content distribution in study area

基于ENVI 5.X软件输出研究区整体建模波段值，输入表现最好的SVM预测模型，得到研究区有机质含量分布预测(图4)。在图中可以清晰地观察到田埂上栽种的树木等异常值，田块间界限清晰。研究区整体土壤有机质含量主要分布在30～40 g·kg-1，中部偏东部地区有机质含量偏高，可能是由于偏东部地区远离主干道，作物类型不统一，不同地块休耕时间不同，本底值更易得到较好的恢复。偏西部地区由于交通便利，大面积种植同一作物，因此，有机质分布情况较为平均。由此可知，对于容易受到人类活动影响的地区，可以通过增加作物种类、轮作休耕等方法减少耕地有机质流失，促进土壤有机质恢复、积累。

3 结论与讨论

本研究以海拉尔地区典型黑土区为研究对象，基于135个土壤样点的有机质含量数据和对应时相的Landsat8影像数据，对影像波段反射率进行主成分分析等4种数学变换，并通过贡献率结合相关性分析筛选得到6个最佳特征波段，采用PLSR、BPNN、SVM方法分别建立了3种土壤有机质含量预测模型，并进行验证，主要结论如下。

(1)休耕时期的农田影像波段数据经过预处理后与土壤有机质含量相关性较高且显著，经不同数学变换后，对应波段与有机质含量间的相关性有所提高，说明数学变换能够扩大数据中对有机质含量变化敏感的细微吸收特征，突出光谱信息，从而更好地用于土壤有机质含量预测。

(2)基于PLSR标准化模型对经不同处理后的光谱反射率结合相关系数进行贡献率分析，可以发现波段对于土壤有机质含量建模的贡献率与相关系数并非绝对相关，筛选最佳特征波段时需结合这2类系数进行分析。

(3)在基于最佳特征波段建立的3种土壤有机质含量预测模型中，SVM模型略优于BPNN模型，优于PLSR模型。SVM方法核函数的参数能够通过自动优化的方法得到，避免了局部最小点、过学习等缺陷，提高了建模精度。本研究检验集中SVM模型的R2最高(0.89)，RMSE为2.81 g·kg-1，RPD为2.14，相比而言，此模型的预测能力最强，为本次研究中最优的黑土区土壤有机质含量预测模型。

(4)PLSR模型与BPNN、SVM模型相比，预测效果较差，主要是由于矩阵转换不可逆，加上默认变量间为线性关系；因此，通过降维处理非随机问题时会造成数据信息缺失，具有一定的局限性。BPNN和SVM模型属于深度学习模型，在本研究中预测效果较好，但仍存在一定程度的误差。这主要是由于研究区面积较大，种植作物、基础肥力、施肥情况不同，造成土壤有机质含量分布存在差异，从而对模型的预测精度造成了一定影响。今后，可以先基于田块种植作物类型对样本数据进行分类，再开展有机质含量预测研究，通过与粗糙集理论结合，从而获得更理想的预测结果。

本研究表明，采用遥感影像数据能够实现对黑土区土壤有机质含量的大尺度预测和快速监测，有助于促进对黑土区的保护和利用。在后续工作中，如何减少环境因素干扰和正确处理样本数据，仍值得进一步研究探讨。