基于刃边法的模糊图像复原

马云 王成龙 时中荣

摘  要：基于点扩散函数的模糊图像复原是数字图像处理领域的重要研究方向之一，其中点扩散函数的获取一直是研究的一个热点。现围绕散射引起的图像模糊开展研究，采用刃边法采集图像模糊核，以高斯函数为模型拟合出系统的点扩散函数，然后采用逆滤波完成图像复原。仿真实验表明，拟合出的点扩散函数较准确，图像复原效果良好。

关键词：点扩散函数;刃边法;模糊;散射;图像复原

0    引言

在图像采集时，对焦不准、运动、大气扰动、散射等原因都会导致图像发生退化，图像清晰程度降低，甚至变得很模糊，丢失很多信息。比如在拍摄运动物体的时候会导致失真，此时获得的图片称为运动模糊，需要对图像进行重构才能变得清楚[1]。当光路中树脂透镜变形、损坏，或者光学元件在透镜组中倾斜会导致成像发生变形，当透镜设计有缺陷的时候也会引起枕形畸变或桶形畸变，这些误差是经常会出现的。在水、雾、毛玻璃等物质的散射作用下，通过成像系统采集的图像会发生退化，分辨率降低甚至发生严重模糊。比如在遥感卫星对地面采集图像时，常因大气的吸收、散射、放射导致图像质量变差，甚至最终导致无法成像。导致图像质量变差的主要原因是散射，大气中的湍流或空气中的水分会导致图像模糊[2]。图像复原的目的就是根据退化原因建立模型，对退化图像进行处理，使其接近原始图像。根据不同的成像模糊原因，需要采用不同的处理方法。

散射导致的图像模糊可以看作是原始图像由于成像系统传递函数存在缺陷导致了退化，从数学角度来说，成像就是原始图像与模糊核发生卷积运算的结果，所以图像的退化可以用式（1）的二维函数来描述[3]。

g（x，y）=f（x，y）×h（x，y）+n（x，y）     （1）

式中：g（x，y）表示退化图像;f（x，y）表示原始图像;h（x，y）表示点扩散函数;n（x，y）表示噪声函数。

式（1）是退化过程在空域的数学描述，也可以用频域表达式来描述，如式（2）所示。

G（x，y）=F（u，v）H（u，v）+N（u，v）         （2）

式中：G（x，y）、F（u，v）、H（u，v）和N（u，v）分别是退化图像、原始图像、点扩散函数和噪声函数的傅里叶变换。

如果噪声很小或者不考虑噪声的影响，那么成像过程可以描述为式（3）。

g（x，y）=f（x，y）×h（x，y）              （3）

在图像复原过程中，噪声也是影响成像质量及复原效果的重要因素之一，是圖像处理中不可或缺的部分，有的图像在复原过程中因为噪声被放大导致图像变得无法分辨。在复原算法中，通常采用逆滤波、维纳滤波对图像进行复原，逆滤波运算快捷，但是抗噪声能力差，在处理含噪图像时，更多会采用维纳滤波。B. Knatarajan提出的基于SVD的图像复原方法，能够在复原图像细节的同时很好地抑制噪声或过滤噪声，对于矩阵中的奇异值也能很好地解决。奇异值本身无论是出现在噪声图像还是估计的模糊核中，都会影响图像的复原效果，而SVD复原方法在去除高斯噪声并保护细节方面很有效[4-5]。

本文在仿真实验中，主要工作围绕点扩散函数的获取开展，所以忽略噪声因素的影响，采用式（3）对成像过程建模。

1    点扩散函数的测量

在理想情况下，理想点光源经过一系列的光学系统后获得图像函数，成像系统或光学系统对理想点光源的脉冲响应称为“点扩散函数”。一幅图像可以看做许多点光源经过系统后在成像器件上的光场叠加，是卷积运算的过程，因此图像复原就成为一个去卷积的运算过程。

在仿真实验中，采用如图1（a）所示的黑白方块作为原始图像，利用黑白边界线在退化前后的变化，对点扩散函数进行估算。实际实验中，对于采集到的彩色图像可以采用单通道的方法进行处理，直接采用某个通道的灰度图就可以完成图像采集。依据散射原理和规律，在实验中图片的仿真退化采用高斯模糊，其中模糊核的大小为50×50（像素），标准偏差为5。

实验中对原始图像与高斯模糊核进行卷积运算后，图像发生退化，特别是黑白分界线变得不再分明，如图1（b）所示，实验采用黑白交界线位置的数据进行测量和拟合。

获得边界像素灰度分布的数据后，对离散数据进行拟合，得到描述边界灰度变化的连续分布函数，如图2所示，其中连续曲线为拟合后的灰度分布函数，折线为原始数据。

2    图像复原实验

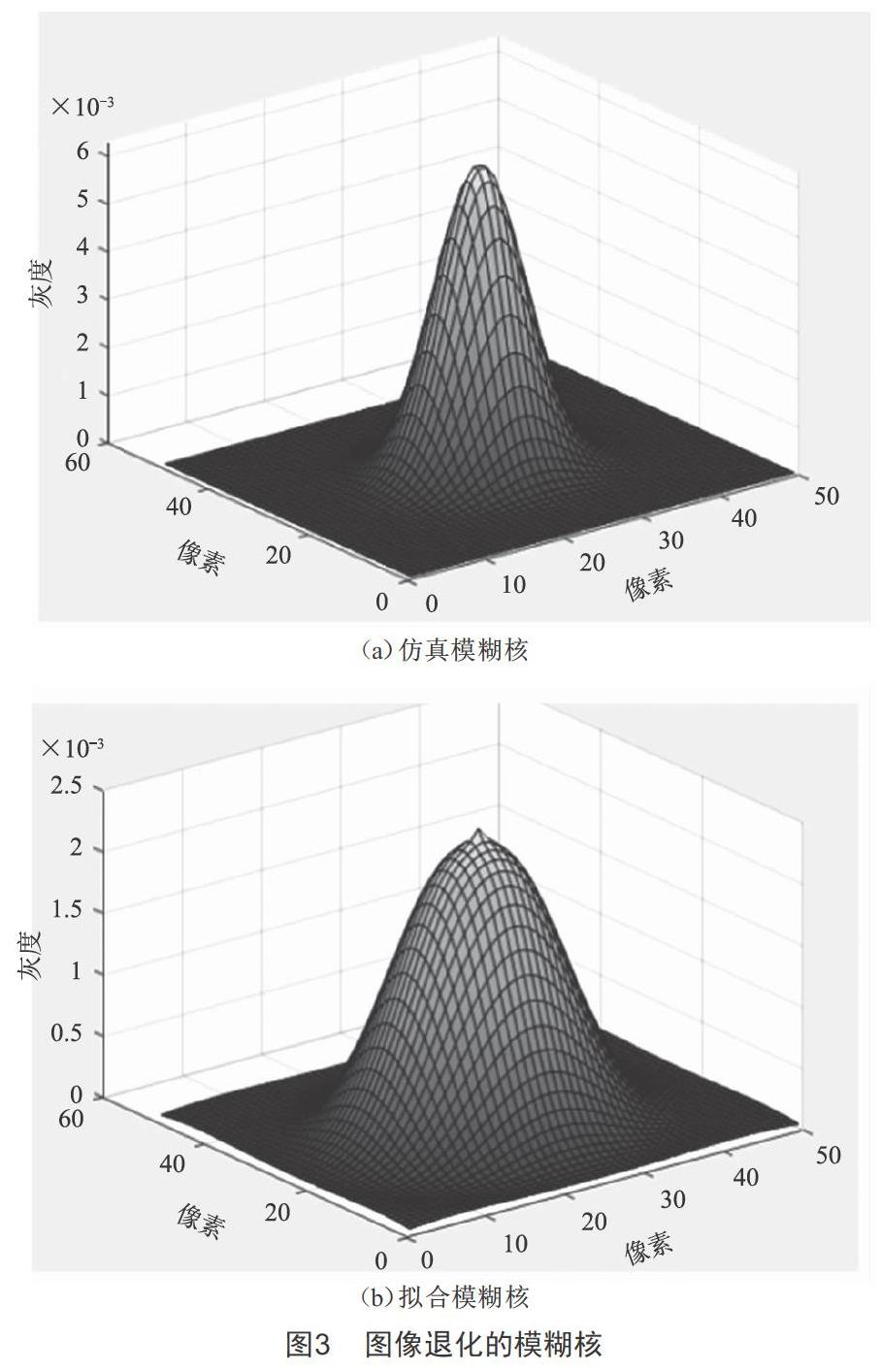
根据拟合获得的线扩散函数，旋转后估算出相应的PSF，如图3所示。

从实验拟合出来的点扩散函数可以看出，拟合的数据会因为模糊核对图片的影响，导致点扩散函数中心不够聚集，这是因为模糊核对图像有平滑作用造成的。从图像中也可以看出，拟合的点扩散函数中间有一个凸起的形状，这是由于中心数据过少导致的拟合不平滑，最后在旋转得到点扩散函数后，中间整体出现凸起，实验中通过空域局部平滑滤波予以消除。

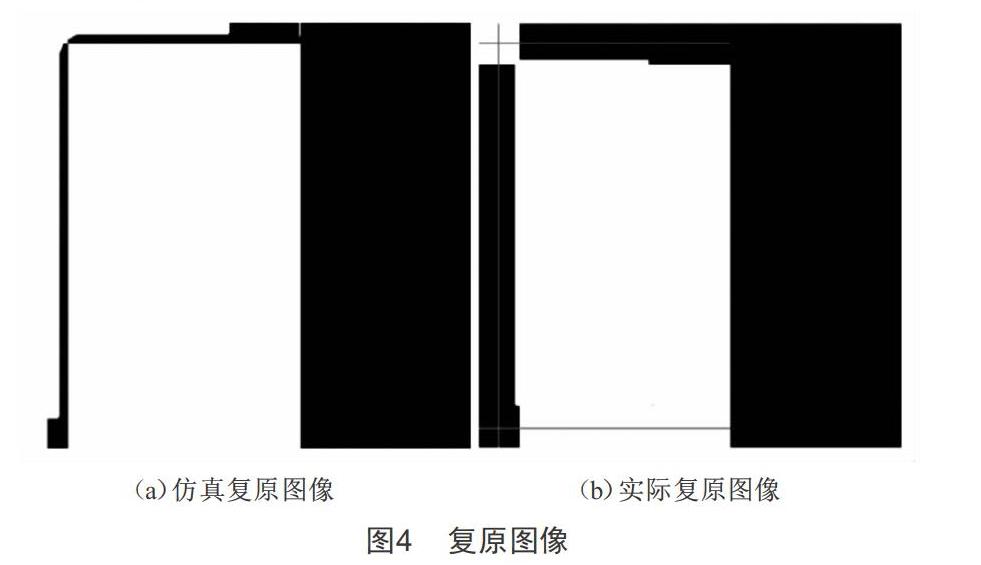
采用拟合的模糊核对退化图像进行复原处理，结果如图4所示。图4（a）是利用仿真模糊核进行的复原处理，可以看出黑白界线分明，复原效果很好;图4（b）采用测量数据拟合出的点扩散函数进行复原，黑白界线分明，复原效果良好，但边缘有轻微失真。

3    结语

本文采用刃边法对模糊图像的点扩散函数获取进行了研究和实验验证，选择黑白图片对成像系统的点扩散函数进行标定，首先测量了退化图像的线扩散离散分布数值，然后拟合出连续分布的线扩散函数，进而估算出系统点扩散函数，并进行了图像复原实验，结果表明，拟合出的点扩散函数较为准确，复原效果良好。

实验中发现，在拟合边缘数据的时候，距离边缘较远的数据要多选取一点，否则在拟合函数图像的边缘时会导致难以收敛。实验中利用边缘扩散函数经过变换得到点扩散函数，其中模糊核大小的估计对结果影响很大，实验中采用了原图像50×50像素的模糊核，在实际图像处理中需要迭代计算出模糊核的分布区域。实验结果出现的偏差除了模糊核误差之外，求解过程中矩阵中数值为奇异值或接近奇异值，都会造成图像处理的结果不理想。

[参考文献]

[1] 孙伟.基于卷帘式快门的数字相机速度测量技术研究[D].长春：长春理工大学，2010.

[2] 朱瑜辉.基于大气散射模型的雾霾天道路图像清晰化[D].北京：北京工业大学，2010.

[3] DASH R，MAJHI B.Motion blur parameters estimation for image restoration[J].Optik-International Journal for Light and Electron Optics，2014，125（5）：1634-1640.

[4] 明文华.运动模糊图像复原算法研究[D].合肥：安徽大学，2004.

[5] BUADES A，COLL B，MOREL J M.A non-local algorithm for image denoising[C]// Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition （CVPR'05），2005：60-65.

收稿日期：2020-06-24

作者简介：马云（1979—），男，安徽六安人，硕士研究生，讲师，研究方向：数字图像处理与智能精密测量。