Azure Kinect DK深度传感器误差分析和修正方法的研究
2020-08-28谢秀齐何演权奉彦文何晓昀
谢秀齐,何演权,奉彦文,何晓昀
(广东理工学院,广东 肇庆 526000)
Azure Kinect DK 是一款开发人员工具包,配有先进的 AI 传感器,适用于复杂的计算机视觉和语音模型。Azure Kinect组合了先进的深度传感器、空间麦克风阵列、摄像机和方向传感器相结合,提供了多种功能。

图1 Azure Kinect 深度相机图
与上一代的产品Kinect for Windows相比,Azure Kinect设备具有更高的硬件规格,同时具备音频、视频、深度和运动传感器,可以全方位感知环境,构建丰富的解决方案。特别提供的深度相机支持工作模式最大提供角度120°×120°,分辨率1024×1024的3D测距功能。
1 Azure Kinect DK测距原理
Azure Kinect DK 使用的测距原理为飞行时间(ToF),其原理与结构光类似采用主动探测机制,通过向待测空间投射光脉冲,根据接收到反射光的相位差计算反射点的深度数据。
ToF 测量原理公式如下

式中,d为深度相机与被测目标之间的距离;c为光速;f为调制频率;Δψ为相位差。
由于光速c和调制频率是确定的,相位差Δψ直接影响着深度传感器的测距精度。依据ToF测距原理可得,光信号通过的光路径与深度数据成正比例关系,表现为光路径越长所获取的深度数据越大,而透镜与被测平面间深度值一致,因此透镜外围部分的测量误差明显大于中心部分的测量误差。如果该深度误差不能得到较好的改正,则深度信息将明显失真,从而影响到三维重建的精度和质量。
2 Azure Kinect DK误差分析
Azure Kinect DK测距的主要误差来源可分为系统误差和随机误差。
2.1 系统误差
系统误差定义为消噪后测得的距离与真实距离之差。 系统误差定义为:
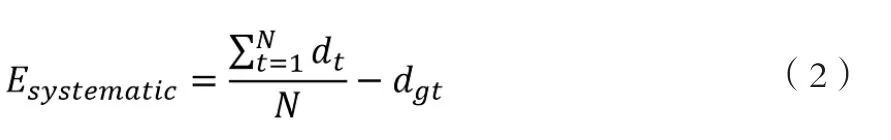
其中,dt表示时间t处的测量距离,N是求平均过程使用的帧数,dgt是真实距离。
2.2 随机误差
假设在没有移动相机的情况下拍摄了同一对象的100 张图像。 在这 100 张图像中,每张图像的对象深度略有不同。 这种差异是散粒噪声造成的。将静态场景中的这种随机误差定义为一段时间内的深度标准偏差,其计算公式为:
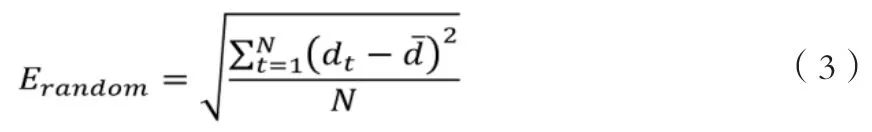
其中,N表示深度测量值数,dt表示时间t处的深度测量值,d表示基于所有深度测量值dt计算出的平均值。
3 试验结果与分析
实验以激光测距仪作为校准设备,其测量精度为1mm。将Azure Kinect DK设备与激光测距仪置于同一水平面,在0.4~12m的方位内移动标靶位置,测得多组测量数据。将测量数据与激光测距仪相对比,得到不同测距范围下深度传感器的测距误差。
3.1 误差分析
将Azure Kinect DK深度传感器获取的测量数据减去由激光测距仪获取的测量数据,得到测距误差随距离分布如图2所示。由图可知Azure Kinect DK测量的深度误差当测量距离小于8.5m时误差较小,基本在2.0mm以内;当测量距离超过8.5m后,深度误差增长明显。
3.2 误差修正
通过对Azure Kinect DK测量的深度数据误差的分析,对比激光测距仪测量数据可以对Azure Kinect DK进行标定,完成对设备的深度数据进行修正,提高深度数据测量的精度。如图1所示,采用多项式曲线拟合算法对测量数据进行拟合获得拟合曲线及拟合公式。其中y为修正后的测量结果,x对应距离。
如图3所示,依据拟合结果对Azure Kinect DK测量的深度数据进行误差修正,使得深度数据在8.5m以内时,其误差小于20mm,在8.5~12m内时,其误差小于50mm,且误差分布较为均衡。
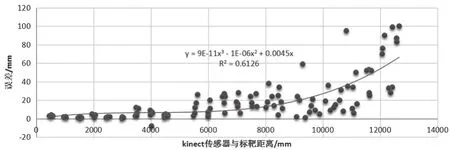
图2 测量误差分布及曲线拟合
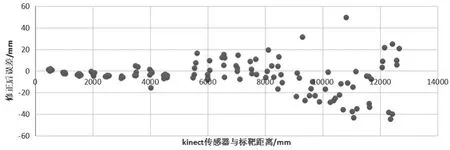
图3 修正后的测量误差分布图
4 结语
本文将Azure Kinect DK深度传感器获取的深度数据与激光测距仪采集的深度数据进行了对比分析,了解其误差与距离变化的关系,并进行了误差修正。实验证明,Azure Kinect DK传感器测量的深度数据误差在8.5m内误差较小;当距离超过8m后,深度误差存在一个较明显的增长,且随距离增加误差也快速增加,测量距离到达12.5m的时候,误差可以达到100mm,且误差均偏向一边。对测量误差结果进行分析可认为误差主要来源是系统误差,可采用多项式曲线拟合方式对测距误差进行修正。修正结果如图3所示,修正后距离在8.5m以内时,误差小于20mm;在8.5~12.5m内时,误差小于50mm,且误差均匀分布在0值上下。修正后Azure Kinect DK的测距精度得到了明显的提高。
