基于Copula 理论的风电出力相关性研究

邢贵阳，刘 莉，庞新富，王 铎

（1.沈阳工程学院a.研究生部；b.学术委员会；c.自动化学院，辽宁沈阳 110136；2.国网辽宁省电力有限公司，辽宁沈阳 110006）

风电作为典型的绿色能源在化石燃料逐渐枯竭的今天有着极为重要的地位，其对电力系统的影响也愈发变得不可忽略，尤其是不同风电场之间的相关性对风电并网规划和运行带来了新的调整。构建风电出力相关性模型以准确描述其相关特性，是当前迫切的需要，对安全、有效地利用风力发电至关重要[1-3]。

当前，风电出力相关性的建模方法主要分为相关系数法和Copula函数法。文献[4]和文献[5]分别是基于相关性系数中的矩相关系数和Spearman 相关系数作为风电出力相关性的建模方法，两者均使用一个固定的相关系数来刻画风电场出力的相关程度，且模型对服从线性、正态分布的风电出力有较好的拟合效果，对变量的分布特性有较高的要求。为解决相关性模型对变量服从正态分布特性的依赖，将经济学分析中的Copula函数引用到风电出力相关性建模的研究中，且取得良好效果。文献[6]利用normal-copula 建立了风电出力相关性模型，将风电相关性加以考虑，用于风电功率预测，所得结论证明了考虑相关性较只针对风电出力的随机性进行预测，能够更为准确地预测风电出力。但normal-copula 本质上还是针对正态分布的风电功率序列进行的研究。文献[7]和文献[8]均应用Gaussian-Copula 对风电出力进行了相关性建模，所得模型较好地描述了风电场之间的相关特性。然而，上述文献虽应用了Copula函数建立了风电出力相关性模型，但并没有刻画相关性的尾部分布特征，且对模型的拟合优度检验方法没有重视，对最优相关性模型的选取较为简略。

本文分别建立了基于5 类Copula 函数的风电出力相关性模型，通过欧氏距离理论作为模型拟合优度检验的方法，并对相关性的尾部特征进行了分析与研究，有效地解决了模型的适用性和拟合优度检验方法中存在的问题。

1 风电出力分布特性分析

对风电出力特性的分析有利于相关性建模方法的选取，提高模型的准确度，应用Jarque-Bera（哈尔克-贝拉）检验分别对两座风电的正态分布特性进行分析。Jarque-Bera 正态检验原理为通过计算基于风电有功出力的偏度和峰度来判定序列是否服从正态分布。设：偏度为g1，峰度为g2，构造一个包含g1、g2的分布统计量（自由度n=2），其统计结果总是非负的，如果结果远大于0，则序列不服从正态分布。在设定合适的显著性水平下，当计算得出的JB统计量小于该序列分布的分位数时，接受假定的H0，即该分布总体服从正态分布；否则拒绝假定的H0，即总体不服从正态分布。

Jarque-Bera统计量定义为

样本偏度g1和样本峰度g2定义式如下：

2 基于Copula 函数理论的风电出力相关性建模原理

2.1 Copula函数理论

Copula函数又称连接函数，它可以将变量的边缘分布和联合分布函数连接在一起，从而可以研究随机变量的相关性，其定义如下：

设随机变量X1,X2,⋅⋅⋅,XN的联合分布函数为H，每个随机变量所对应的边缘分布分别为F1(X1)、F2(X2)、⋅⋅⋅、FN(XN)，则存在一个Cop‐ula函数C，使得

如果边缘分布F是连续的，则联合分布函数C是唯一的。

2.2 Copula函数分类

Copula 函数主要包含5种类型：Gaussian-Cop‐ula、t-Copula、Gumbel-Copula、Clayton-Copula 及Frank-Copula，其中前两种因其密度函数的等高线平面投影为椭圆形，因此得名为Ellipse（椭圆）-Copula 函数，后3 种隶属于Archimedean（阿基米德）-Copula函数族，具体表达式如下：

1）N元Gaussian-Copula函数的分布函数为

式中，φρ为N阶正态分布（其相关系数矩阵为ρ）的分布函数，且其边缘分布是标准正态分布；φ-1为标准正态分布函数的逆函数。

2）N元t-Copula的分布函数表达式为

式中，tρ,k为标准N元t分布的分布函数（其相关系数矩阵为ρ，自由度为k）为一元t分布（自由度为k）函数的逆函数。

3）Gumbel-Copula的分布函数为

式中，α为参数，α∈[1,+∞)。

4）Clayton-Copula的分布函数为

式中，α为参数，α∈((-1,0)⋃(0,+∞))。

5）Frank-Copula的分布函数为

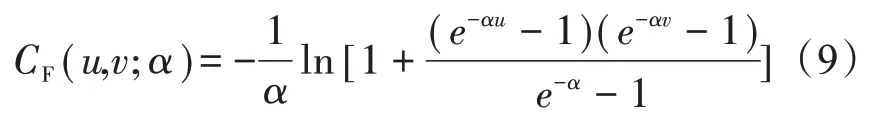
式中，α为参数，α∈((-∞,0)⋃(0,+∞))。

根据5 种Copula 函数描述分布的不同，其描述序列对称性及反应尾部特性情况如表1所示。

表1 5类Copula函数特性

3 拟合优度检验

5 类Copula 函数有其各自的性质，在分别建立基于5 类Copula 函数的相关模型后，需要分别评估模型拟合的优劣，而检验拟合效果通常采用距离检验的方法。本文引入欧氏距离理论，对5 类Copula模型计算其与经验Copula的欧氏距离，从而作为模型拟合优劣的判据，欧氏距离越小，证明其拟合效果越好。

欧氏距离（欧几里得度量）是研究中使用最多的距离度量定义，可计算空间中任意两点间的真实距离，其二维空间两点距离定义式为

该定义可由二维扩展到m维，m维空间两点距离的定义式为

式中，d为点(x1,x2,...,xn)到点(y1,y2,...,yn)之间的欧氏距离。

4 仿真分析

4.1 风电出力特性及正态分布检验

选取辽北地区两座在地理位置相近且装机容量相似的风电场作为仿真算例，两风电场装机容量等基本装机情况如表2所示。

表2 两风电场基本装机情况

两座风电场在2018 年的有功出力如图1、图2所示。

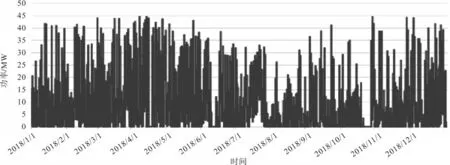
图1 风电场1全年有功出力

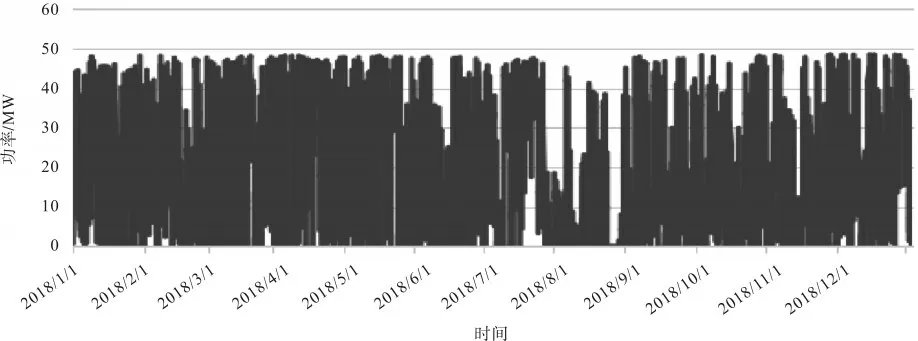
图2 风电场2全年有功出力

应用JB 法分别对两座风电场进行正态分布特性的检验，返回值均为1，即拒绝风电场出力服从正态分布的原假设，因此两座风电场不能应用相关系数法建立相关性模型，而采用Copula 函数法，检验结果如表3所示。

表3 Jarque-Bera（JB）正态分布检验

4.2 相关性模型构建及拟合优度检验

根据Copula函数定义，联合分布函数可分解为5 类Copula 概率密度函数及边缘分布函数，通过累计概率函数计算式，拟合Copula函数的累计分布函数，由此生成基于Copula函数的风电出力相关性模型。两风电场联合分布函数如图3所示。

图3 两风电场联合分布函数

通过计算5 类Copula 函数与经验Copula 函数的欧氏距离，对模型进行拟合优度检验，经验Copu‐la 函数的累计概率密度函数如图4 所示，拟合优度检验结果如表4所示。

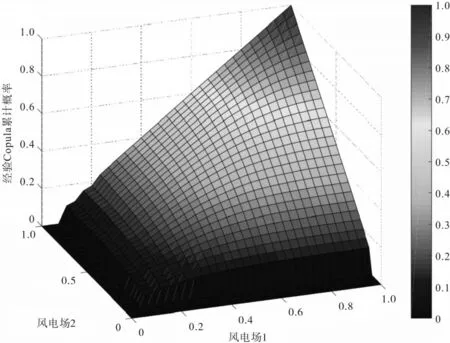
图4 两风电场经验Copula累计概率密度

表4 各类Copula与经验Copula欧氏距离

从表4 可以看出，基于Gumbel-Copula 函数所建立的风电出力相关性模型为两座风电场的最佳相关性模型。图5、图6 所示分别为基于Gumbel-Copula函数的累计概率密度及概率分布图。

图5 Gumbel-Copula函数累计概率密度

图6 Gumbel-Copula函数概率分布

通过对比图4与图5发现两个图像具有基本一致的分布特征，可以进一步验证拟合优度检验的结果。从图6 可以看出两风电场的相关性特征，在对角线即两风电场出力相差不多时，其具有明显的相关性，随着向上尾和下尾延伸相关性逐渐增强，具有极其明显的尾部分布特征，并且两风电场同时出力较大时的相关程度是同时出力较小时的数倍。

5 结论

本文针对基于相关性系数建立的风电出力相关性模型对非线性及非正态分布特性的风电出力拟合效果较差的问题，建立了基于Copula函数的风电出力相关性模型，并应用基于欧氏距离理论的相关性拟合优度检验方法对所建模型拟合效果进行了检验，结果发现Gumbel-Copula 为两风电的最佳相关性模型，其相关特性表现为两风电场出力相近时的相关程度较大，并具有明显的尾部特征，当两风电场出力出现两极化时，其相关性几乎可以忽略。