灰岩山区降雨入渗补给系数取值研究

薛明霞 孙 明

（山西省水文水资源勘测局太谷均衡实验站 山西太谷030800）

山丘区地下水资源量通常是根据补排平衡原则，利用水文测验成果分析得到。基于山西的特殊情况——采空区集水、超采区水位恢复等，形成地下水滞蓄，无法以基流形式排泄。而利用补给法计算山丘区地下水资源量，计算方法概念清晰，资料条件明确，能够反映区域的地下水形成、储存、运移等条件，体现了计算方法的客观性。

补给法计算山丘区地下水资源量，就是利用山丘区的降雨入渗补给系数进行计算。山丘区的降雨入渗补给系数是地质、地貌、生态环境和人为环境的综合系数，受区域地质构造、地形地貌、岩类裸露程度、地表环境、地下水埋深、人为因素等影响，相同岩性的下垫面不同区域的降雨入渗补给系数存在差异，实验区取得的降雨入渗补给系数不能直接应用于下垫面岩性相同的其他区域。

由于影响山丘区降雨入渗补给系数的因素复杂，且各因素对区域降雨入渗补给系数的影响程度不同、与降雨入渗补给的定量关系获取困难，因此，本文旨在寻找一种方法，通过一定的途径，确定山丘区各因素对降雨入渗补给系数的综合影响程度，建立实验区综合影响程度与其降雨入渗补给系数的关系，从而确定其他区域的降雨入渗补给系数。山丘区下垫面岩性主要有灰岩、变质岩、砂页岩和黄土，受资料限制，本文仅对灰岩山区的降雨入渗补给系数取值进行研究。

1 影响因素

影响灰岩山区降雨入渗补给系数的因素主要有：岩类的构造（岩溶）发育程度、岩类的裸露程度、地表-地下流域边界是否一致、地下水埋深、森林覆盖面积、灌丛覆盖面积、地形地貌、水利工程情况、人为活动影响、水文有效断面控制情况、水土保持措施等，本文选择了8个概念清晰易懂、物理意义明确、且能够通过标准的测定方法或规范的统计方法确定或者能采用定性描述的因素，确定其对降雨入渗补给系数的综合影响程度。

所选择的8个影响因素及其意义见表1。

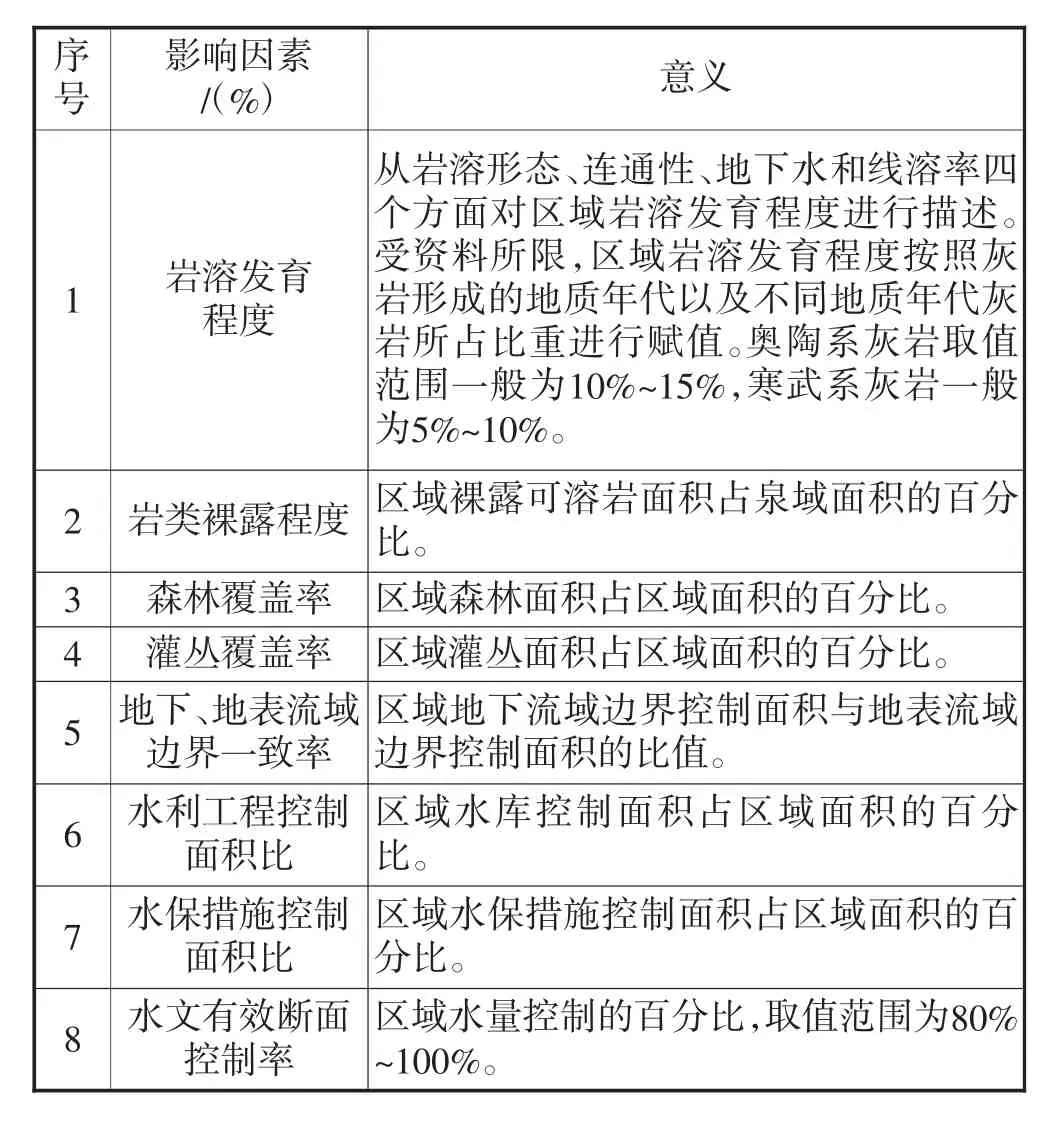
表1 灰岩山区降雨入渗补给系数影响因素

2 研究区域

选择1个实验区和6个计算区进行研究。1个实验区为灰岩山区的岔上水文站，6个计算区为6个水资源分区的灰岩山区。6个水资源分区[1][2][3]为西北的红河区、偏关-吴堡区、吴堡-龙门区，东南的沁河区、丹河区、卫河区。

岔上水文站：位于芦芽山森林区，控制面积为32.1 km2，下垫面类型为灰岩森林山地，以寒武系灰岩为主。森林覆盖率为96%。

红河水资源分区：位于山西省北部，灰岩部分面积为821.4 km2，覆盖有部分灌丛，面积为244.2 km2，灰岩为奥陶系灰岩和寒武系灰岩，基本上各占一半。区域内中小型水库累计控制流域面积为764 km2。

偏关-吴堡水资源分区：位于山西省西北部，灰岩部分面积为4 226.5 km2，其中森林覆盖面积为574.5 km2，灌丛为2 998.6 km2，灰岩为奥陶系灰岩和寒武系灰岩，奥陶系灰岩占多数。据不完全统计，区域内中小型水库累计控制流域面积为594 km2。天桥泉的大部分泉域和神头泉、柳林泉的小部分泉域位于本区内，泉域总面积为13 974 km2，灰岩出露面积为3 422 km2。

吴堡-龙门水资源分区：位于山西省西南部，灰岩部分面积为1 601.8 km2，其中森林覆盖面积为898.0 km2，灌丛为703.8 km2，灰岩为奥陶系灰岩和寒武系灰岩，以奥陶系灰岩为主，寒武系灰岩零星分布。柳林泉的大部分泉域和郭庄泉、龙子祠泉的小部分泉域位于本区内。泉域总面积为4 729 km2，灰岩出露面积为1 454 km2。据不完全统计，区域内中小型水库累计控制面积为936.4 km2。

沁河水资源分区：位于山西省南中部，灰岩部分面积为1 590.2 km2，其中森林覆盖面积为764.6 km2，灌丛为825.6 km2，灰岩为奥陶系灰岩和寒武系灰岩，以奥陶系灰岩为主。区域内岩溶地貌发育，岩溶泉水出露点多、点低。延河泉的大部分泉域和霍泉的部分泉域位于本区内。泉域面积2 575 km2。据不完全统计，区域内中小型水库累计控制面积967.5 km2。

丹河水资源分区：位于山西省东南角，灰岩部分面积为1 037.2 km2，其中森林覆盖面积为292.4 km2，灌丛为744.8 km2，灰岩为奥陶系灰岩和寒武系灰岩，以奥陶系灰岩为主，寒武系灰岩零星分布。区域内岩溶地貌发育，岩溶泉水出露点多、点低。主要岩溶大泉有白洋泉，三姑泉，三姑泉的上游沿丹河河谷还有三姑泉群的多处泉水出露，较大的有郭壁泉、土坡泉、台北泉、白洋泉、小会泉等。三姑泉泉域总面积为2 814 km2，包括丹河流域的大部分区域。据不完全统计，区域内中小型水库控制面积为618.85 km2，有中小型灌区9个。水保治理面积为10.47万hm2，治理度44%。

卫河水资源分区：位于山西省东南角，灰岩部分面积为1 579.5 km2，其中森林覆盖面积为914.2 km2，灌丛为665.3 km2，灰岩为奥陶系灰岩和寒武系灰岩，以奥陶系灰岩为主，寒武系灰岩零星分布。区域内有小型水库1座，控制面积42 km2。

根据研究区域基本情况，通过查阅有关文献、实地调研等方式确定灰岩山区区域影响因素特征值见表2。

3 综合影响程度

本文利用模糊可变评价模型[4][5]评价灰岩山区各影响因素对降雨入渗补给系数的综合影响程度。

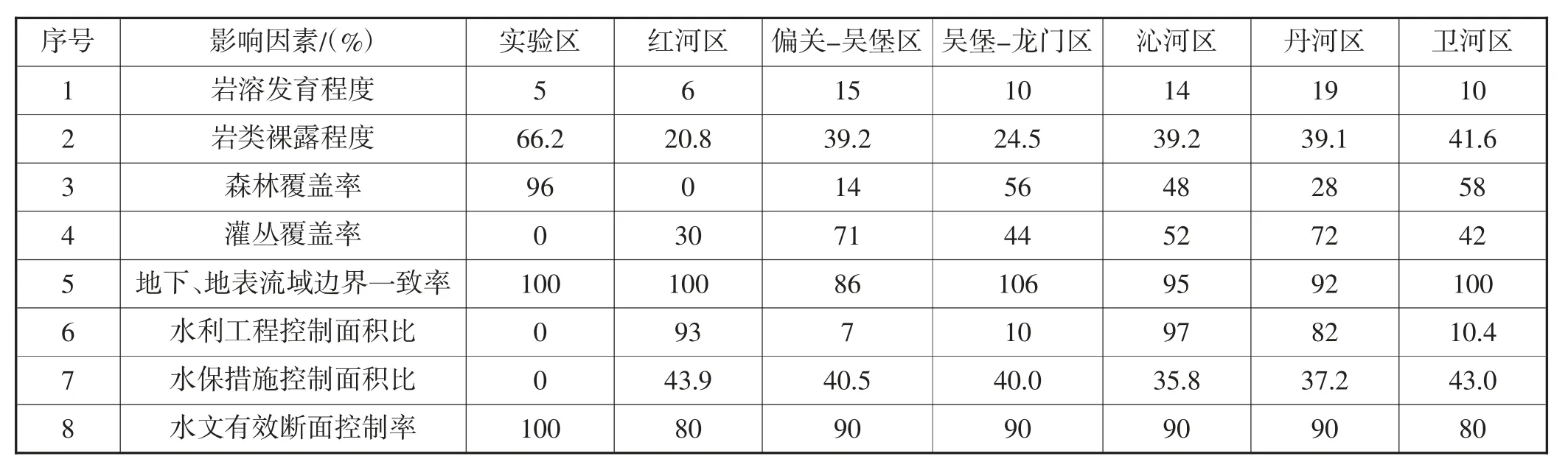
表2 灰岩山区区域影响因素特征值

3.1 建立评价指标体系

灰岩山区各影响因素对降雨入渗补给系数的综合影响程度评价指标体系（以下简称评价指标体系）分为目标层和指标层两个层次。目标层是评价的总目标，表达的是灰岩山区降雨入渗补给系数影响因素的综合影响程度。通过评价区域的综合影响程度，确定区域降雨入渗补给系数，最终确定区域地下水资源量。指标层反映目标层的影响因素，评价指标体系选择前述8个影响因素作为评价指标。

不同评价指标评价的标准不同，需确定不同评价指标相同判断级别的标准值，将各评价指标的特征值与其标准值相比较，合成一个综合评价结果。

本文参考相关标准、以往研究成果以及有关专家意见，结合区域评价指标的特征值，制定各评价指标的分级标准值（阈值），将每个评价指标相应地划分为4个等级，1级优于2级，2级优于3级，4级最差。评价指标体系及指标标准值见表3。

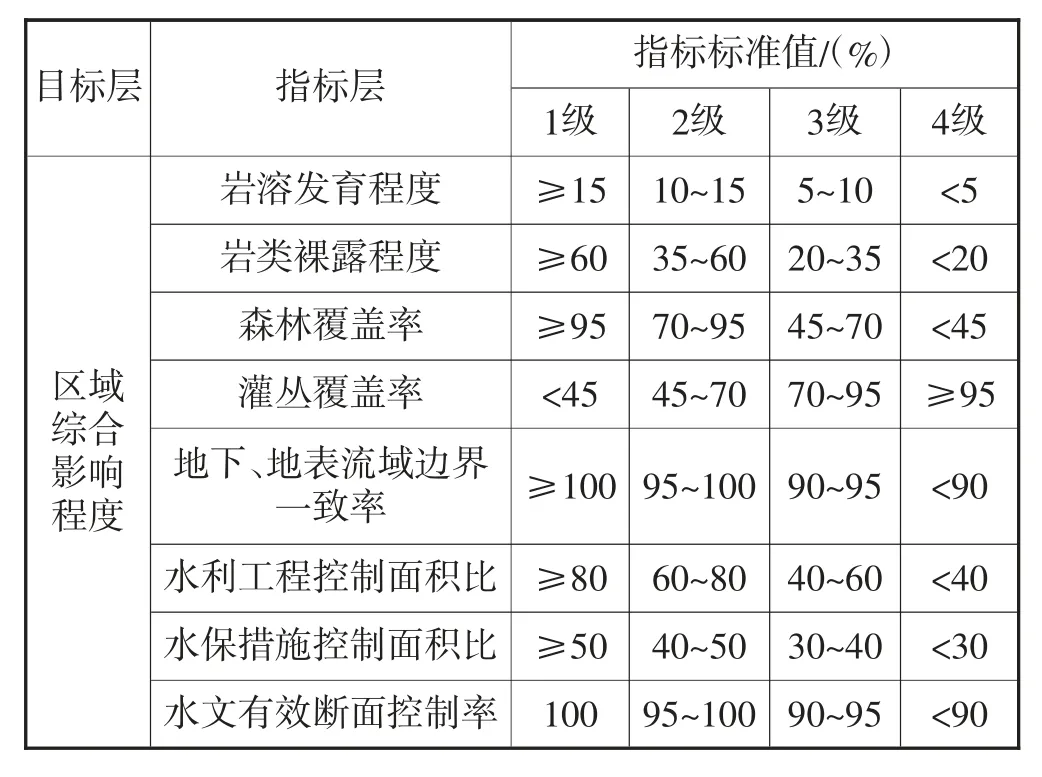
表3 评价指标体系及指标标准

3.2 综合影响程度评价

3.2.1 评价过程

1）建立指标特征值矩阵

根据表2，对降雨入渗补给系数的综合影响程度作识别的样本（区域）有7个，每个样本（区域）的特性用8个指标特征值表示，则样本（区域）集用8×7阶指标特征值矩阵X表示：

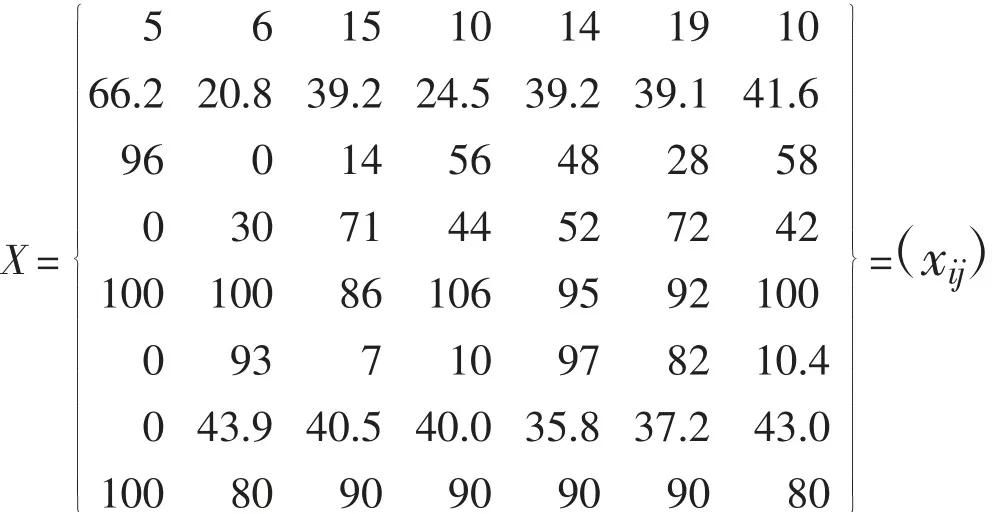
式中：i=1，2，…，8，为指标号；j=1，2，…，7，为样本（区域）号；xij为样本（区域）j指标j的特征值。如：i=1表示第一个指标岩溶发育程度，j=5表示第五个样本（区域）沁河区，x15=14表示样本（区域）沁河区的第一个指标岩溶发育程度的特征值为14。

2）建立指标标准值矩阵

根据表3，样本（区域）集依据8个指标按4个级别的指标标准值进行识别，则有8×4阶指标标准值矩阵Y：

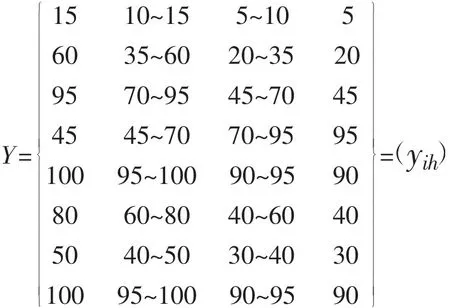
式中：h=1，2，3，4，为评价等级；yih为级别h指标i的标准值。如：i=1表示第一个指标岩溶发育程度，h=3表示评价等级3，y13为5～10表示评价等级为3时第一个指标岩溶发育程度的标准值在5～10之间。

3）确定指标标准值区间矩阵

样本（区域）按4个级别进行评价，并设定1级优于2级，…，4级最差。根据指标标准值矩阵和区域的实际情况确定指标标准值区间矩阵Iab：

矩阵Iab为可变模糊集理论中模糊可变集合的吸引（为主）域区间矩阵，是已知矩阵。指标标准值区间［aih，bih］有两种情况：（1）aih＜bih，称为递增系列，相当于指标特征值越小，其级别越优。②aih＞bih，称为递减系列，相当于指标特征值越大，其级别越优。如：i=1表示第一个指标岩溶发育程度，h=3表示评价等级3，［a13，b13］=［10，5］，a13=10，b13=5，a13＞b13，表示评价等级为3时第一个指标岩溶发育程度的标准值区间为［10，5］，且第一个指标岩溶发育程度的标准值为递减系列，其特征值越大，级别越优。

4）确定范围域矩阵

根据矩阵Iab中各级指标标准值区间两侧相邻区间的上下限值确定指标i级别h的范围值区间［cih，dih］，范围域矩阵Icd：

如：i=1表示第一个指标岩溶发育程度，h=3表示评价等级3，则c13=a12=15，d13=b14=0，即［c13，d13］=［15，0］，表示评价等级为3时第一个指标岩溶发育程度的范围值区间为［15，0］。

5）确定点值矩阵

根据矩阵Iab，按物理分析与实际情况确定吸引域区间［aih，bih］中相对差异度等于1，即DA（xij）h=1的点值矩阵M：

点值Mih：当h=1，2，3时Mih=aih，当h=4时Mih=bih。

当xij=Mih时，DA（xij）h=1。如：i=1表示第一个指标岩溶发育程度，h=3表示评价等级3，M13=10，当j=4（第四个样本（区域）吴堡-龙门区）时x14=10，则DA（x14）3=1。

6）确定相对隶属度矩阵

样本（区域）j指标i对各级别的指标相对隶属度矩阵Uh为：

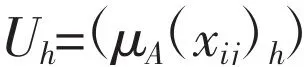
其中：相对隶属度μA（xij）h=（1+DA（xij）h）/2

相对差异度：DA（xij）h

当待评价样本（区域）j指标i的特征值xij落在Mih值的左侧，即xij＜Mih，采用式（1）计算：

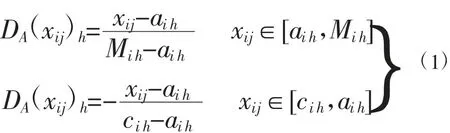
当待评价样本（区域）j指标i的特征值xij落在Mih值的右侧，即xij＞Mih，采用式（2）计算：

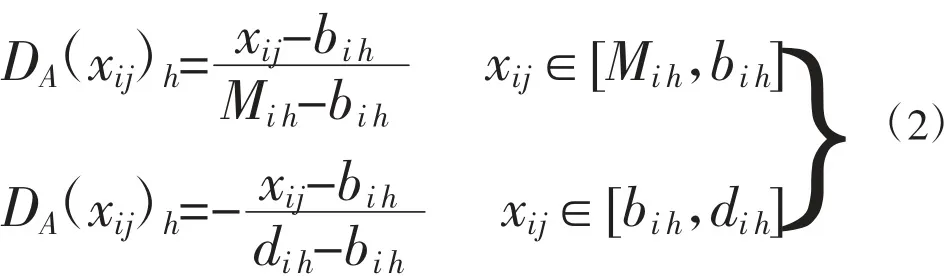
根据矩阵Ia b、Ic d和M，判断样本（区域）j指标i的特征值xij选择公式（1）或（2）计算相对差异度，再根据相对隶属度公式确定指标相对隶属度矩阵。

以样本（区域）j=2，指标i=4时的特征值x42对评价等级h=1为例计算相对隶属度。

根据指标特征值矩阵X，样本（区域）j=2，指标i=4时的特征值x42=30，根据点值矩阵M，i=4，h=1时M41=0，由于x42＞M41，因此选择式（2）计算。又由于x42介于M41与b41之间（根据吸引（为主）域区间矩阵，i=4，h=1时b41=45），因此选择式（2）中第一式进行计算。则DA（xij）h=（30-45）/（0-45）=0.333，μA（xij）h=（1+0.333）/2=0.667。

经计算得到相对隶属度矩阵：

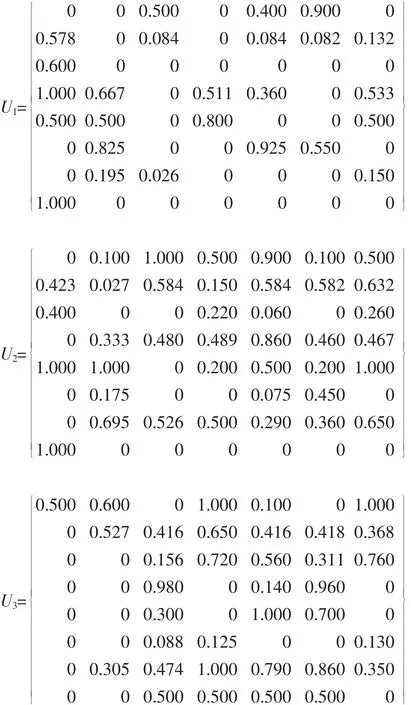
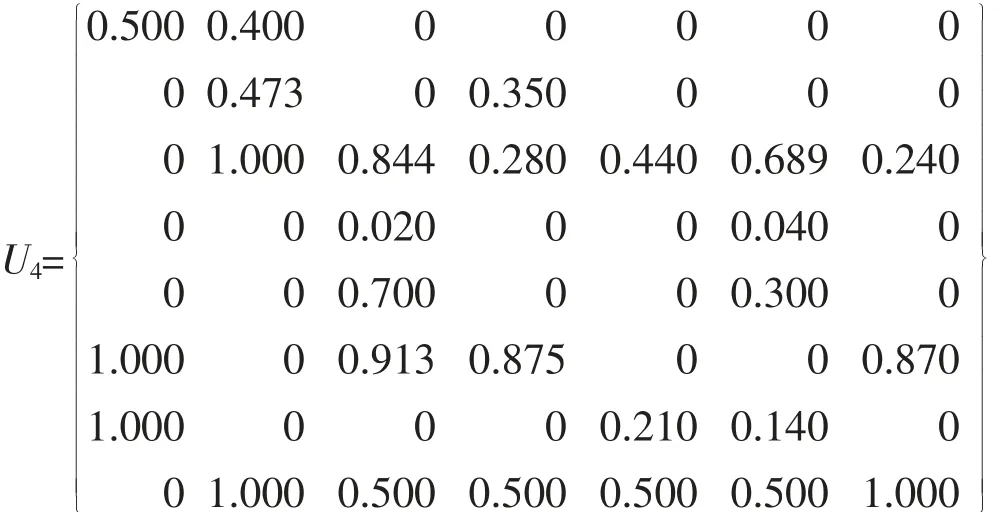
7）确定评价指标权重

在灰岩山区降雨入渗补给系数取值影响因素影响程度综合评价中，合理确定指标权重是非常重要的。指标权重不同，将会导致不同的评价结果。本文选择当前比较通行的层次分析法（简称AHP,Analytic Hierarchy Process）。

第一步，建立递阶层次结构模型，此处即为评价指标体系的目标层和指标层。

第二步，构造判断矩阵。一般采用1～9比例标度对指标重要性程度赋值，标度及其含义见表4。

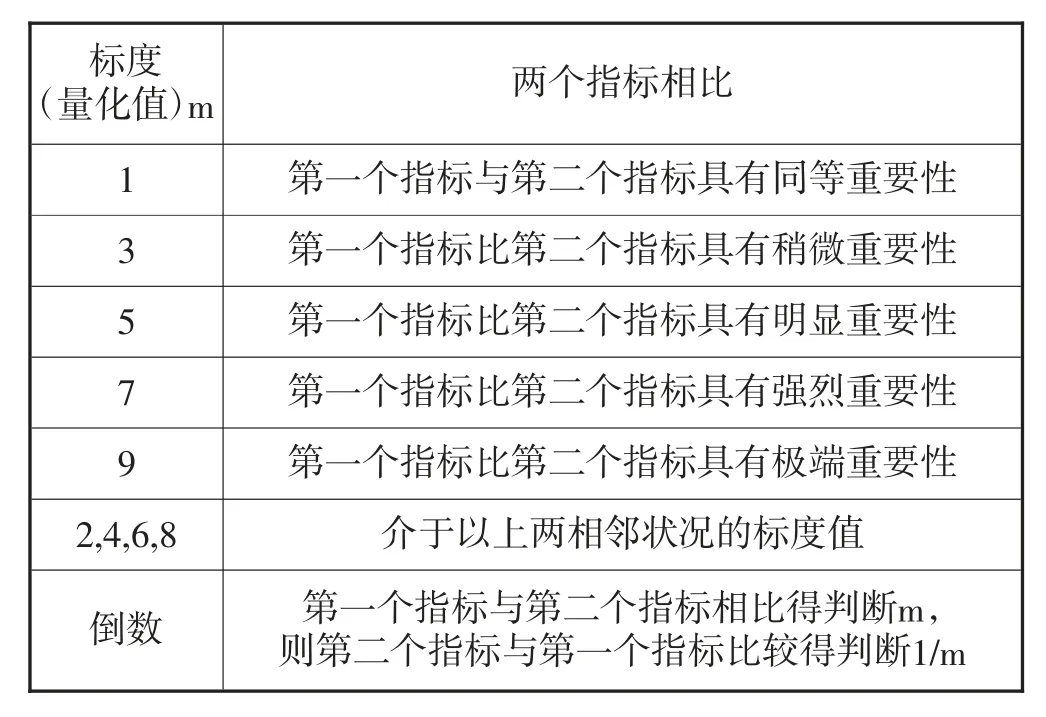
表4 1～9标度法

遵循层次分析原理，依据标度法，结合有关专家意见，对各指标的重要性程度进行赋值。

赋值过程为：岩溶发育程度与岩类裸露程度相比，认为岩溶发育程度比岩类裸露程度的重要性介于明显重要和强烈重要之间，因此标度值取6；反之，岩类裸露程度与岩溶发育程度相比，取岩溶发育程度与岩类裸露程度相比标度值的倒数，即取1/6。岩溶发育程度与森林覆盖率相比，认为岩溶发育程度比森林覆盖率明显重要，因此标度值取5。反之，森林覆盖率与岩溶发育程度相比，取岩溶发育程度与森林覆盖率相比标度值的倒数，即取1/5。依次对各指标进行赋值，赋值结果见表5。依据表5即可确定判断矩阵。

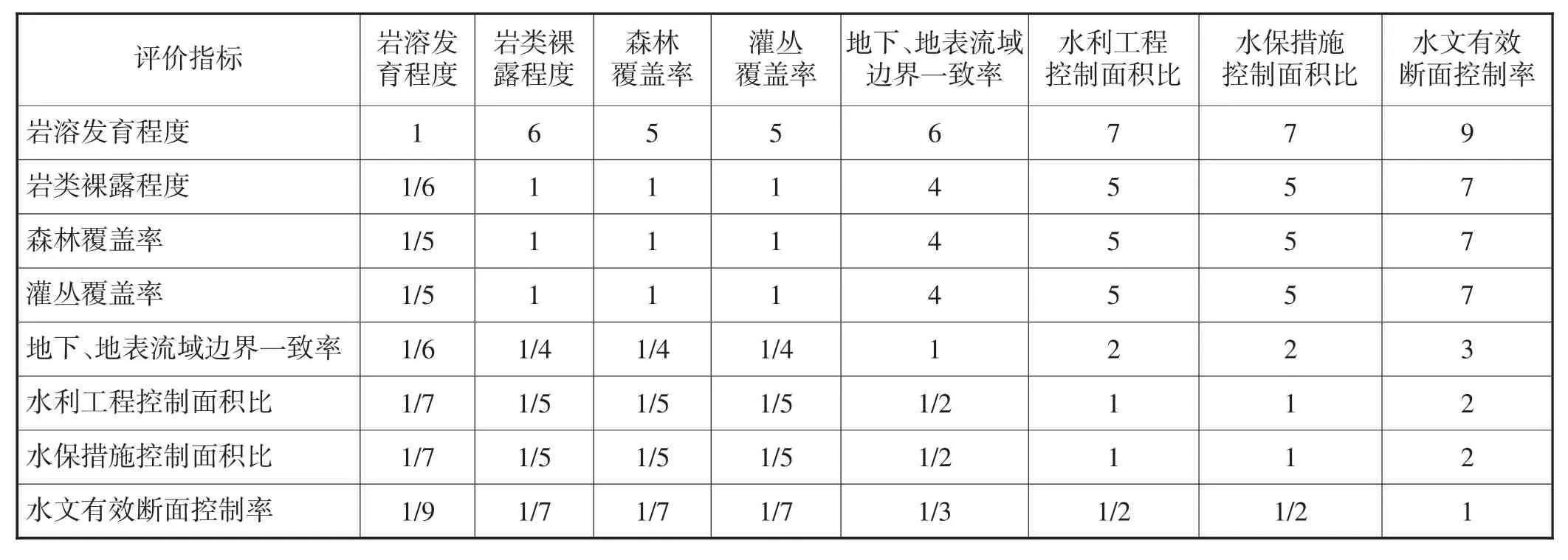
表5 层次分析标度法赋值表

第三步，计算单一准则下元素的相对权重并进行一致性检验。

经计算，判断矩阵的最大特征根为8.4252，评价指标的非归一化权向量W′=（3.280，1.166，1.182，1.182，0.440，0.286，0.286，0.180），则评价指标的归一化权向量W=（0.4100，0.1458，0.1477，0.1477，0.0550，0.0357，0.0357，0.0225）。

一致性检验：如果随机一致性比率CR＜0.1，则判断矩阵具有满意的一致性。式中CI为计算一致性检验指标，CI=其中λmax为判断矩阵的最大特征根，n为判断矩阵阶数；RI为随机一致性指标，取值与n有关。

则CR=（8.4252-8）/（8-1）/1.41=0.04＜0.1（n=8时，RI=1.41），则判断矩阵具有满意的一致性。评价指标权重见表6。

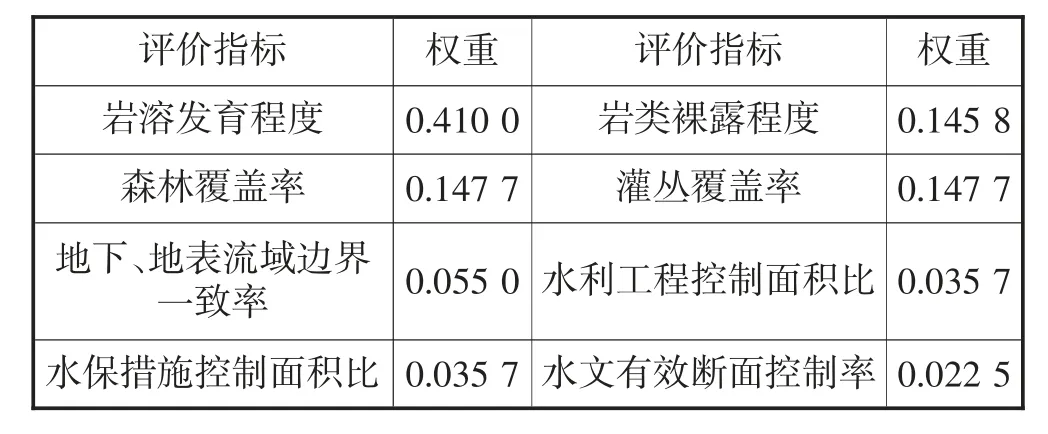
表6 评价指标权重

8）计算综合相对隶属度

应用模糊可变识别模型

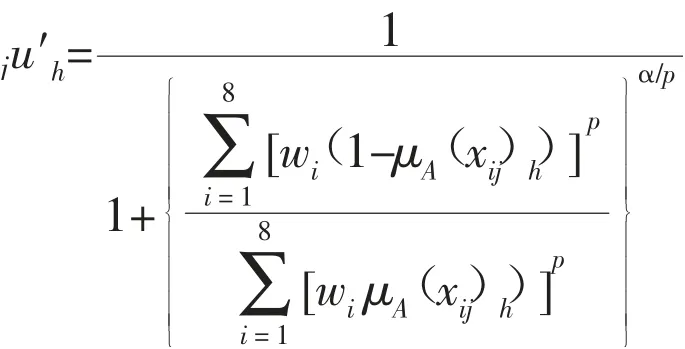
（其中α为模型优化准则参数，α=1为最小一乘方准则，α=2为最小二乘方准则；p为距离参数，p=1为海明距离，p=2为欧氏距离；wi为指标权重；i为识别特征指标。）计算样本（区域）对各级别的综合相对隶属度j u′h，得到非归一化的综合相对隶属度矩阵U′=（ju′h），将其归一化处理得到综合相对隶属度矩阵U：U=（juh），其中α=1，p=1时

应用级别特征值公式H=（1，2，3，4）·U，得到区域影响因素的级别特征值向量H：

由此得到评价结果见表7。

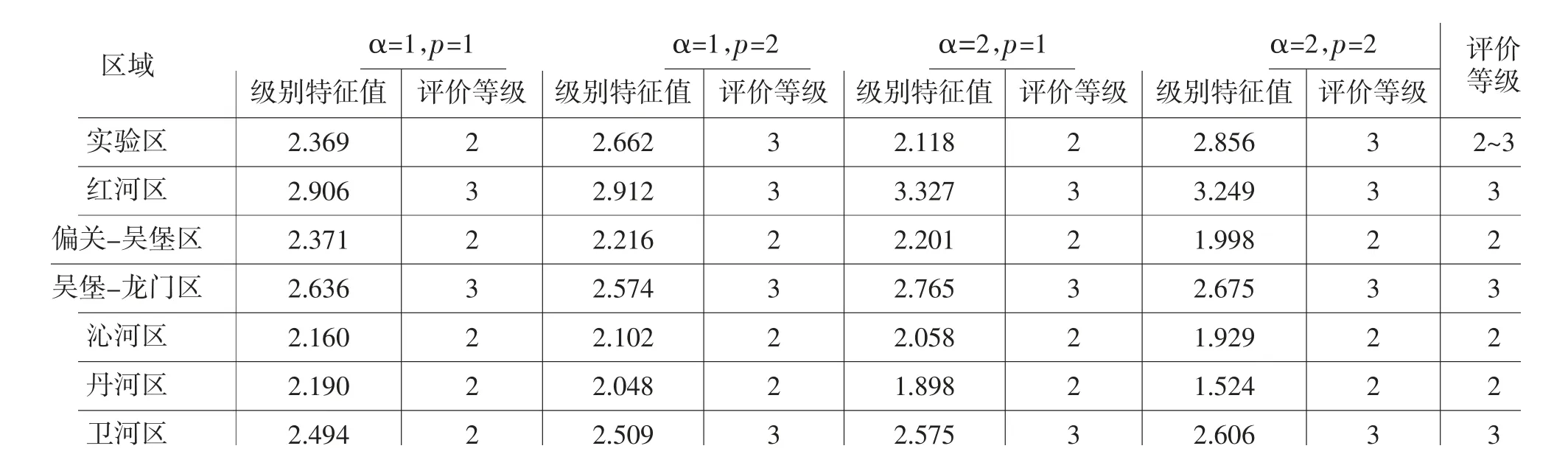
表7 区域灰岩山区综合影响程度评价结果

3.2.2 评价结果

区域灰岩山区综合影响程度评价等级反映了各影响因素对降雨入渗补给系数的综合影响程度。据表7，评价等级为2级～3级，则综合影响程度为2～3。说明不同区域，由于岩溶发育程度、灰岩裸露程度、森林、灌丛的覆盖率、地下、地表流域边界的一致率、水利工程控制情况、水保情况、水文有效断面控制情况等的不同，对其降雨入渗补给系数的综合影响程度不同，其降雨入渗补给系数也就不同。

4 综合影响程度与降雨入渗补给系数的关系

区域灰岩山区综合影响程度介于2～3之间，考虑计算精度，将综合影响程度保留一位小数，则实验区的综合影响程度为2.5，计算区的综合影响程度见表9。

受各影响因素综合影响程度的影响，灰岩山区降雨入渗补给系数存在差异，但分布在一定范围内。利用区间估计原理，依据三σ准则，以实验区实际综合影响程度和其对应的降雨入渗补给系数为基准，确定实验区其他综合影响程度对应的降雨入渗补给系数以及其相对于实际综合影响程度对应的降雨入渗补给系数的变化程度。

实验区其他综合影响程度对应的降雨入渗补给系数计算公式为：

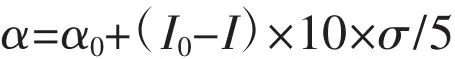
式中：α——实验区其他综合影响程度I对应的降雨入渗补给系数；

α0——实验区实际综合影响程度I0对应的降雨入渗补给系数；

I0——实验区实际综合影响程度（评价结果）；

I——实验区其他综合影响程度，介于1～4之间；

σ——实验区降雨入渗补给系数标准差。

实验区其他综合影响程度对应的降雨入渗补给系数相对于实际综合影响程度对应的降雨入渗补给系数的变化程度η计算公式为：

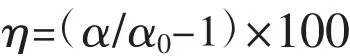
式中符号意义同前。

以实验区多年平均降雨量在600～700 mm之间的降雨入渗补给系数为例，进行说明。

实验区多年平均降雨量在600～700 mm之间的降雨入渗补给系数为0.177，标准差σ=0.05，即实验区综合影响程度I0=2.5时降雨量在600～700 mm之间的降雨入渗补给系数α0=0.177，以I0=2.5，α0=0.177为基准，计算实验区其他综合影响程度的多年平均降雨量在600～700 mm之间的降雨入渗补给系数及其相对于实际综合影响程度对应的降雨入渗补给系数的变化程度，计算结果见表8。

实验区综合影响程度与变化程度的关系同样适用于其他区域灰岩山区。

根据表8的实验区综合影响程度与变化程度的关系和表9的计算区综合影响程度，确定计算区多年平均降雨量在600～700 mm之间的降雨入渗补给系数相对于实验区实际综合影响程度对应的降雨入渗补给系数的变化程度，见表9。

表8 实验区综合影响程度与变化程度关系表（降雨量600～700 mm）

对于相同区域，不同降雨量级别，其降雨入渗补给系数的变化程度是相同的。因此，计算区的降雨入渗补给系数的变化程度见表9。

表9 计算区综合影响程度与变化程度关系表

根据实验区不同降雨量级别的降雨入渗补给系数和计算区降雨入渗补给系数的变化程度，确定计算区的降雨入渗补给系数，见表10。

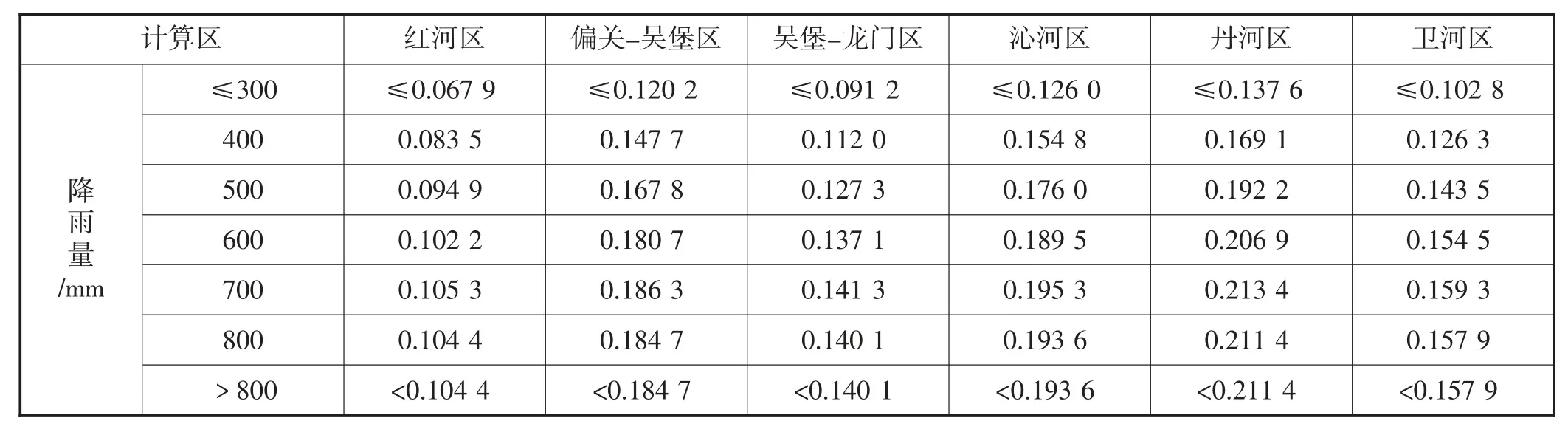
表10 计算区降雨入渗补给系数表

5 补给法计算区域灰岩山区地下水资源量

灰岩山区地下水资源量主要是指通过裸露灰岩的降雨入渗补给量和渗入到浅埋区土壤并在重力作用下渗透补给岩溶的地下水量。计算公式为：

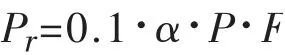
式中：Pr——区域降雨入渗补给量，万m3；

α——年降雨入渗补给系数，（α=f（P））；

P——年降雨量，mm；

F——计算面积，km2。

根据表10中的计算区降雨入渗补给系数，计算1980-2000年系列计算区的地下水资源量，结果见表11。

表11 1980-2000年系列计算区地下水资源量计算表

补给法计算灰岩山区地下水资源量，反映了区域地下水形成、储存、运移等条件；补给系数是地质、地貌、生态环境和人为环境的综合系数；补给计算概念清晰，资料条件明确，体现了计算方法的客观性。

6 结论

本文是在灰岩山区实验区降雨入渗补给系数研究的基础上，利用实验区降雨入渗补给系数影响因素的综合影响程度与降雨入渗补给系数变化程度的关系，得到计算区降雨入渗补给系数的变化程度，从而得到计算区的降雨入渗补给系数。

灰岩山区降雨入渗补给系数的取值研究，从方法上降低了计算地下水资源量的人为影响，为灰岩山区补给法计算地下水资源量提供了计算保证。

对于灰岩山区确定降水入渗补给量和入渗补给系数是一个比较复杂的问题，作者就本文进行了大胆尝试，有许多问题还没有认识，有待进一步探索。