基于MATLAB的年最高潮水位极值Ⅰ型分布频率分析计算
2020-08-27许弘喆程素珍
许弘喆, 程素珍
(1.兰州大学, 甘肃 兰州 730107; 2.山东省水利科学研究院, 山东 济南 250013)
极值Ⅰ型、皮尔逊Ⅲ型分布曲线是进行最高潮水位频率分析的主要理论频率曲线[1],目前利用MATLAB开发环境进行皮尔逊Ⅲ分布曲线计算较多[2],如孙玉芳[3]的基于MATLAB开发环境的皮尔逊Ⅲ型频率曲线分析软件开发,李扬[4]的极值指数估计在太原站月降水频率分析中的应用研究等,均利用MATLAB软件进行皮尔逊Ⅲ型频率曲线分析[5-11]。但有关利用极值Ⅰ型分布进行最高潮水位频率分析的应用较少,且多侧重于序列特征参数估计和计算方法对比研究,基本没有涉猎基于极值Ⅰ型分布适线法在工程中的应用研究,现有相关规范均为参数查表、公式计算相应频率下的水文特征设计值的计算方法。为推广普及极值Ⅰ型分布在最高潮水位频率分析中的应用,开发一种应用软件是十分必要的。本文结合威海石岛海阳观测站年最高潮水位频率分析,开发了一款基于MATLAB软件应用环境下,极值Ⅰ型分布适线法在最高潮水位频率分析计算中的应用,并成功在工程中应用,取得了理想效果。
1 极值Ⅰ型分布理论
极值分布是指在概率论中极大值(或者极小值)的概率分布,耿贝尔在1941年首次将极值Ⅰ型分布应用于洪水频率分析工作,其密度函数符合降雨、径流、潮水位等水文参数的分布规律。因此广泛应用于水文特征参数的频率分析计算。
假设某观测站历年水位特征观测值为h1,h2,…hn,观测值呈极值Ⅰ型分布,则极大值h的分布函数为:
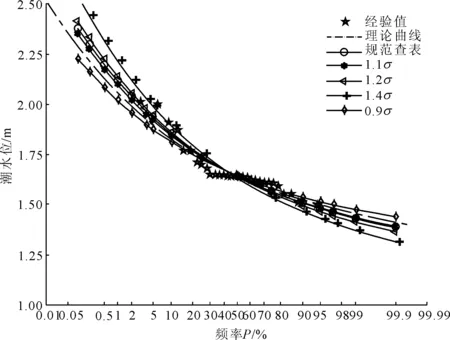
F(hp)=f(h (1) 水位序列均值和均方差采用矩法进行估算,见公式(2)、公式(3)。 (2) (3) 式中:hi为序列第i年的年特征水位;n为年最高水位序列项数。 在水工设计中,通常用超越概率来表征设计频率,即 p=p(h≥hp)=1-F(hp)=1-e-e-α(hp-β) (4) 对式(4)两边取2次对数有: (5) 把α、β化简代入式(5)得: (6) 令: λpn=-(0.45+0.78×ln(-ln(1-p))) ,式(6)转化为: (7) 首先建立观测数据样本矩阵,x1、x2……,可以单独对样本进行分析,也可以通过cat(1,x1,x2,……)语句进行样本矩阵合成分析。 矩法实现参数的统计语句是: fori=1∶n u=u+X(i)*X(i); end 最大似然法通过mle语句实现参数的统计,即: p=mle('ev',x); σ=p(2) 经验频率是验证各项计算成果的重要依据,根据经验频率公式求出相应水位的经验频率值,绘制经验频率点,并与相应的计算成果相对比,进行相应的水位值和参数的合理性分析。经验频率计算方法为:在n项连序水位系列中,按大小顺序排位的第m项水位的经验频率Pm,采用下列数学期望公式计算: (8) 式中:m为水位连序系列中的序位;Pm为第m项水位的经验频率。 MATLAB软件的实现方式是: n=length(X);X=sort(X);X=fliplr(X); Pm=[[1∶n]/(n+1)] 适线法是在一定的适线准则下,求解与经验点据拟合最优的频率曲线的统计方法,可避免因观测序列短而产生计算结果可靠性差等问题。采用矩法或最大似然法对观测数据序列进行统计,求出一组参数作为初值计算理论曲线,根据理论频率曲线与经验频率点据的配合情况,通过经验判断调整适配参数,选定一条与经验点据拟合良好的频率曲线。 适线法计算过程:(1) 统计水位连续观测年最大值,建立水位观测序列,并依数值大小排列成递减序列,根据式(8)按序号确定逐项的经验频率,将逐项数值和频率点绘在黑森机率格纸上;(2) 统计计算的水位序列的均值、均方差一组统计参数,该组参数作为适线法初值;(3) 根据极值Ⅰ型分布理论,采用初值计算理论频率曲线;根据理论频率曲线和经验频率点的拟合程度,保持均值不变,通过经验判断调整均方差,一般采用0.1倍的数值增减,重新拟合频率曲线,并把每次拟合的频率曲线连同经验点据绘制在同一张机率格纸上,进行比较分析,选定一条与经验点据拟合良好的频率曲线,这条线即为经验频率曲线,通过该线查找相应设计频率的潮水位。 通过初估、适线和综合对比分析,可以得到比较合理的、能够满足工程设计要求的水位经验频率曲线。通过选定的经验适线,根据极值Ⅰ型理论计算相应设计频率的特征参数,并且可借助经验频率曲线的延长,推求相应稀遇频率的特征参数设计值。 适线法计算能够通过MATLAB软件中的Evinv、Evcdf函数实现,能同步完成数据的统计、分析、绘图和曲线拟合,并采用Norminv函数生成黑森机率格纸,成果显示在同一张机率格纸,便于评价和分析。 最高潮水位频率计算中采用的黑森机率格纸是一种特殊的坐标系统,其纵坐标为均匀分格的常规数学坐标,横坐标与频率值的标准正态分布分位数有关。由于标准正态分布分位数在P=50%处为零,而黑森机率格纸在P=0.01%时的横坐标值为零。它是实现最高潮水位频率分析成果的重要工具,MATLAB软件可通过调用Norminv函数实现,具体的程序语言为: PL=[0.01 0.05 0.5 1 2 5 10 20 30 40 50 60 70 80 90 95 98 99 99.9 99.99]; xx=norminv(PL/100,0,1); yy=[1∶0.25∶2.5]; axis([min(xx),max(xx),min(yy),max(yy)]) set(gca,‘xtick’,xx,‘ytick’,yy) set(gca,‘xticklabel’,PL,‘yticklabel’,yy) grid on 图、表是计算分析结果的主要表现形式,清晰、美观、准确的图表格式便于设计人员的利用,MATLAB软件具有强大的图表生成功能,可以根据客户的要求进行定制,下面是一个简单的表格生成程序语言: mab1=cat(1,chengguo1,chengguo2,………); data=mab1; f=figure(1); colnames={‘0.1%’,‘0.2%’,‘0.5%’,‘1%’, ‘2%’, ………}; rnames={‘First’,‘Second’,‘Third’,‘f’,‘t’}; t=uitable(f, ‘Data’, data, ‘ColumnName’,colnames, ...‘RowName’, rnames...‘Position’, [20 80 500 200]); 程序运行完成后,计算结果立即以图、表的形成呈现,满足设计人员的分析和评价,但是MATLAB生成的图、表为图片格式,不便编辑,为此MATLAB设计了与其他软件的连接功能,便于格式的转换。 MATLAB提供使其能与Excel互动操作的Excel-link宏。Excel-link 使得数据在MATLAB与Excel之间随意交换,以及在Excel下调用MATLAB的函数,它将MATLAB强大的数值计算功能、数据可视化功能与Excel的数据Sheet功能结合在起,因此可以把MATLAB生成的计算数据导入Excel进行编辑和应用。 (1) 运行MATLAB程序,调入编好的*.m程序文件。 (2) 把原始资料输入*.m程序的原始参数矩阵,根据资料类型,修改预先定义的图表和坐标名称。 (3) 根据工程需要,选定序列特征参数的估算方法。 (4) 运行*.m程序,即生成**工程水位累计频率曲线和和**工程成果汇总表。 (5) 根据经验频率曲线选择原则,对生成的各条频率适线和经验频率点据相比较,若成果符合要求,计算完毕;否则,调整适配参数,重新运行*.m程序,直到获得满意的成果,计算完毕。成果格式见图1和表1。 图1 年最高潮水位频率曲线 (6) 把计算成果图片导入Excel,进行编辑,表1为经Excel编辑的表格格式。 表1 工程设计水位计算成果表 (1) 利用MATLAB软件编程进行极值Ⅰ型频率分析,能够把资料汇总、经验频率点据、适线参数估算、多条适线拟合计算和成果生成同时完成,具有程序简单、高效以及计算精度高的特点,便于在实际工作中推广应用。 (2) MATLAB简单易学,编制的程序结构简单,功能齐全,修改方便,可以使工程设计人员从繁重的资料整理、复杂运算中解脱出来,大大提高水利工作者的工作效率。
2 MATLAB实现最高潮水位频率分析的原理和方法[12-16]
2.1 MATLAB实现参数估计


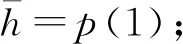
2.2 MATLAB实现经验频率计算
2.3 MATLAB实现极值Ⅰ型分布理论计算
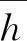
2.4 MATLAB能同步实现适线法拟合
2.5 MATLAB软件实现黑森机率格纸生成[13]
2.6 图表成果生成[14-15]
3 工程实例


4 结 语
