探讨综合法和分析法在初中几何解题中的应用
2020-08-25戴燕红
戴燕红
(江苏省天一中学 214101)
几何解题需要清醒的头脑与沉稳的心情,不要一看到几何证明题目凭着自己的直觉就开始着手解题,首先需要运用分析法细致、全面地分析几何题目的解题思路,然后再运用综合法对几何题目整体把控,开始证明.分析法讲的是以所要证明的几何题目结论为出发点,向前一步步寻找使其成立的充分条件,直到找到一个符合题目的条件.
综合法讲的是在几何题目证明当中,通过已知条件开始证明,解题过程环环相扣,最终得到几何题目所要证明的结论成立,简而言之就是通过已知去看可知,步步接近未知的证明方法.综合法是初中几何试题常用的解题方法.
一、综合法和分析法在初中几何解题中的应用
例1 如图1所示,三角形ABC是一个等腰直角三角形,CF是直角∠ACB的角平分线,BF是外角∠ABE的角平分线,CF与BF这两条角平分线相交于点F,探求∠BFC与∠BAC之间的数量关系.

解根据已知条件,∠ACB=90°,CF是∠ACB的角平分线,所以∠CAB=∠BCF=1/2∠BCA=45°.因为BF是外角∠ABE的角平分线,所以∠ABF=1/2∠EBA=1/2(180°-∠CBA)=1/2(180°-45°)=67.5°.所以∠FBC=67.5°+45°=112.5°,所以∠BFC=180°-∠FBC-∠BCF=180°-112.5°-45=22.5°.又因为∠CAB=45°,所以∠BFC=1/2∠BAC.
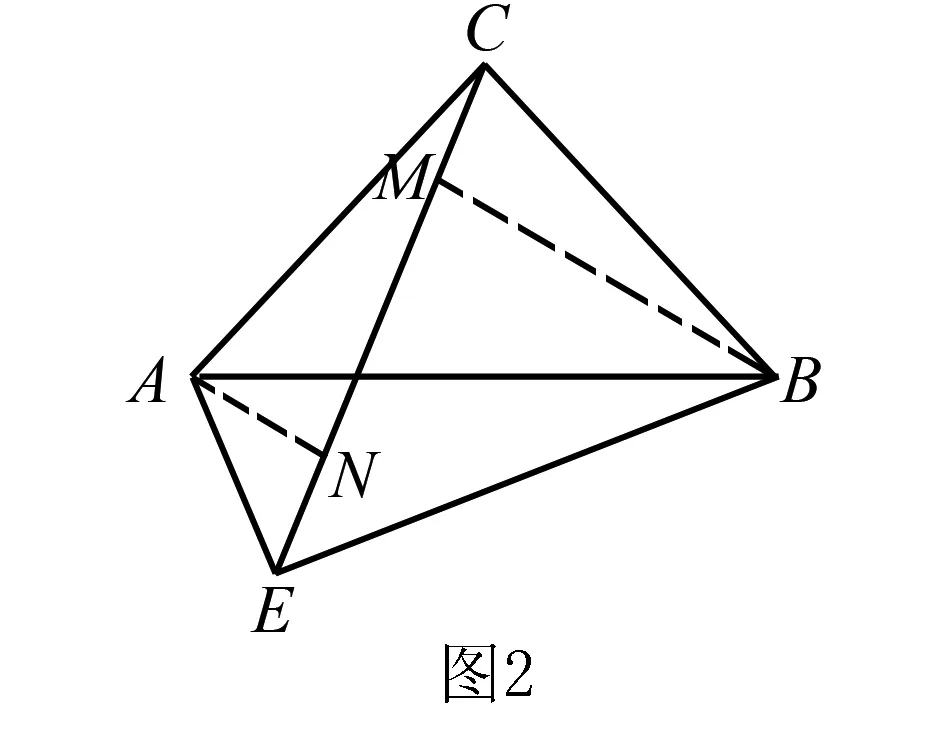
例2 如图2所示,在等腰Rt△ABC中,∠ACB=90°,点E是△ABC之外的一点,并且∠AEC=45°,求证线段AE⊥BE.
首先运用分析法探索几何题目的解题路线:若证明线段AE⊥BE,已知∠AEC=45°,需要证明∠BEC=45°.分析到这里,解题遇到第一个瓶颈,没有更多的已知条件可用,我们需要考虑借助辅助线来增加已知条件,通常会首先考虑具有特殊性的45°角.继续分析:作线段BM⊥EC并相交于点M,须证明线段BM=EM,线段BM处在△BMC当中,通过看图直觉发现并没有与其全等的三角形,因此还需要增加一条辅助线构建一个与三角形BMC全等的三角形.已知AC=BC,作线段AN⊥EC相交于点N,得出AN=EN,进而可以运用角角边的全等三角形定理证明△CBM全等于△ACN,进一步得到线段BM=CN.因为线段CM=AE=EN,所以线段CN=EM,所以线段BM=EM,所以∠BEC=45°.进而得出所需要求证的结论,线段AE⊥BE.
二、激发学生几何学习兴趣,促进综合法和分析法在初中几何解题中的应用
兴趣是最好的老师,学生自身对几何学习产生兴趣直接促进综合法和分析法在初中几何解题中的应用.
首先,教师可以举出几何学习中具有代表性、通俗易懂的背景材料.举例来讲,教师在传授学生“平行线”这一概念的时候,教师可以先让学生们观察铁轨的图片、长方形黑板的左右边缘、直尺的上下边缘等,引导学生发现以上例子具有哪些共同点.学生在观察、分辨之后,老师可以让学生举手发言,同时通过举手数量来初步衡量学生们的观察情况,然后教师顺理成章地将本节课“平行线”的概念引出来,学生们就更容易理解“平行线”这一抽象的概念了.
其次,可以通过就具体的实验来调动学生学习几何的积极性,恰到好处地使用几何教学工具就显得尤为重要,老师指导学生自己动手开展几何实验,引导学生主动探索几何的奥秘,由此一来,不仅在几何情景课堂创设方面收获意想不到的良好效果,同时还有助于培养初中学生的学习能力.比如,在学习证明三角形全等、角与角之间的关系时,教师可以向学生们发出疑问,两个三角形三个角的度数都一样就是全等三角形吗?学生们几乎都回答是,然后老师拿出两个角度相同但边长不等的两个三角形卡片,让学生们动手将两个三角形重合,学生们在亲自动手实践之后发现,两个三角形卡片大小不一致,根本不能说是全等三角形.学生们会继续思考,具备怎样的条件才能是全等三角形?进而对初中几何的学习兴趣愈加浓厚.
在初中数学学习当中,几何部分的学习对于初中生来讲非常重要,也是很多学生认为较难的学习内容,很多几何图形较为抽象,需要学生在脑海中建立立体模型,所以,在初中几何学习中,教师要逐步降低几何题目的解题难度,对学生看到几何题目后的解题思路与寻找解题路径能力方面进行强化,可以借助图形、添加辅助线等来找到解题思路,帮助学生正确运用综合法和分析法,帮助学生很快解决几何试题的求证,提高学生几何解题能力.加强师生之间的沟通与交流,重点监督学生几何试题解题思路能力的掌握程度以及几何图形绘图能力.在学生掌握基础知识的同时,重点指导学生综合法和解析法在初中几何解题中的应用情况.
