从大学生数学竞赛谈重积分换元法

滕吉红， 鲁志波， 黄晓英

(信息工程大学 基础部，河南 郑州 450002)

0 引言

为增加大学生学习数学的兴趣，培养分析、解决问题的能力，发现和选拔数学创新人才，为青年学子提供展示基础知识和思维能力的舞台，中国数学会自2009年开始举办全国大学生数学竞赛，到目前已经成功组织过10届。竞赛分非数学专业和数学专业，分为初赛、复赛和决赛，初赛和决赛是全国统一命题，复赛一般是各省自行命题选拔。结合历届初赛和决赛试题，通过分析非数学专业的初赛和决赛试题中所涉及的多元函数积分学的题目，从考查的频率和考查方式说明了换元法在求解多元函数积分问题时的重要应用，最后从方法论的角度给出了这部分内容的教学建议。

1 竞赛试题分析

非数学专业初赛和决赛历届竞赛试题的题目主要包括填空题、计算题和证明题等，初赛考试内容仅限于高等数学，决赛内容涉及高等数学和线性代数两门课程，所占比例分别是80%和20%。虽然所涉及的内容均不超过理工科相应课程教学大纲的规定，但试题还是有较强的综合性和较大的难度。多元函数积分学的内容是历届初赛、决赛都会涉及的知识点，主要包括二重积分、三重积分、曲线积分以及曲面积分等，而这些问题的解决中很多用到了重积分的换元法，具体如表1所示。可以发现，初赛、决赛20套题中涉及多元函数积分学的共有37道，考查的频次是非常高的，其中应用到重积分换元法的有23题，占62%，足以说明重积分换元法在解决一些难点问题中的重要性和有效性。

表1 竞赛试题中重积分的换元法Tab.1 Exchange element method of multiple integrals in mathematics competitions

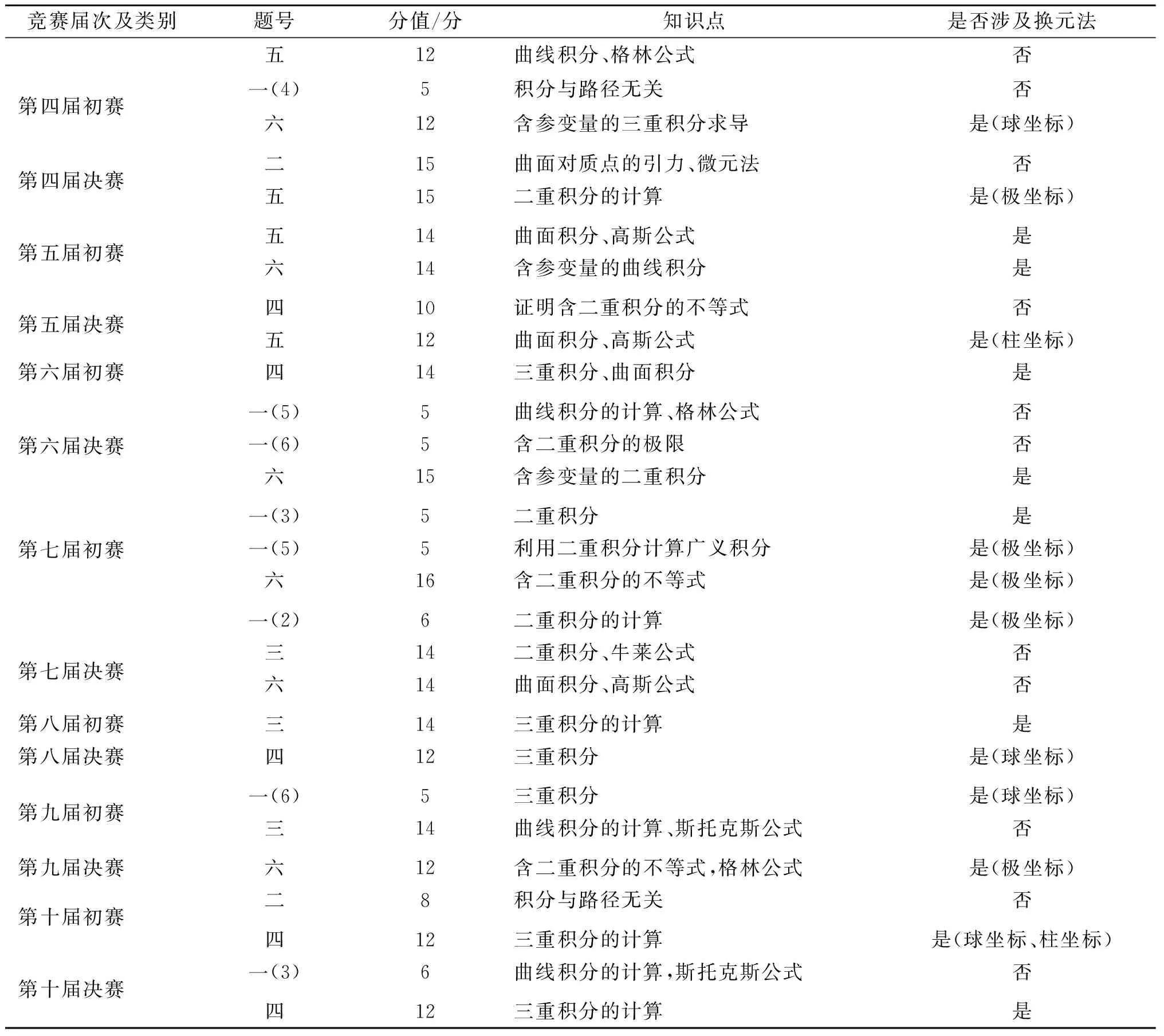
续表1 竞赛试题中重积分的换元法 Tab.1(Continued) Exchange element method of multiple integrals in mathematics competitions

2 重积分的换元法

在定积分的计算中，通过换元法，可以使积分变得简单易求。同样，在二重积分的计算中，也可以利用换元法简化计算，我们以二重积分为例。

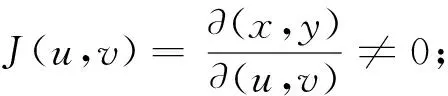
类似地，三重积分也有换元法，在这里不再详述。

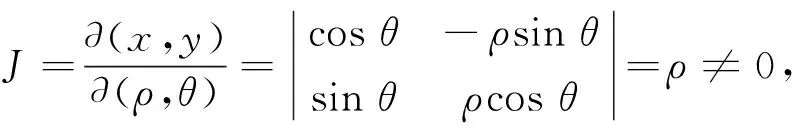
柱坐标变换可以看作三重积分换元法的特殊情况，即令x=ρcosθ,y=ρsinθ，z=z，则雅可比行列式为

则有

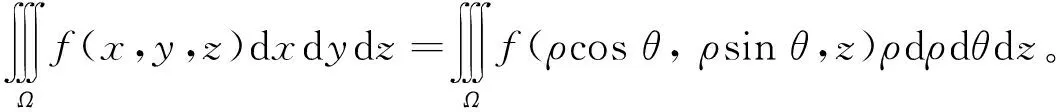
球坐标变换可以看作三重积分换元法的特殊情况，即令x=rsinφcosθ,y=rsinφsinθ,z=rcosφ，则雅可比行列式为

则有

由表1可以看出，二重积分的极坐标，以及三重积分的柱坐标、球坐标都是多元函数积分学部分考查的重点。

3 方法论角度下的教学建议

二重积分换元法和三重积分换元法在高等数学教学大纲中的要求不高，均为“了解”，因此大多数高等数学教材[1-2]中都把重积分的换元法作为选学内容，标记为“*”号，受高等数学课程学时的限制，很多高校在教学中都会把这部分内容删去不讲。而学习数学的最高境界是数学联系哲学[3]，哲学是数学更深刻的思想基础[4]。从哲学的范畴来看，作为“了解”的重积分换元法和要求“熟练掌握”的极坐标换元法、柱坐标换元法以及球坐标换元法之间是一般与特殊的关系，所以从方法论的角度，建议把重积分的换元法作为讲授内容，这样可以引导学员站在更高的维度上思考问题，构建系统完整的知识框架体系，培养有效的数学思维和哲学思维。