规划模型在数学建模中的应用
2020-08-24刘晓妍
刘晓妍
(山东科技大学 基础课部,山东 济南 250031)
1 问题的提出
该问题取自2011年全国大学生数学建模竞赛D题中的一部分[1]。
天然肠衣(简称肠衣)制作加工是我国的一个传统产业,传统的生产方式依靠人工,将原材料按指定根数和总长度组装出成品(捆)。原料按长度分档,通常以0.5 m为一档,如14.0~14.4 m按14.0 m计算,14.5 m~14.9 m按14.5 m计算,以此类推。表1是某种成品规格,长度单位为 m,∞表示无上限,但实际长度不足26.0 m,表2为某批原料描述。

表1 成品规格
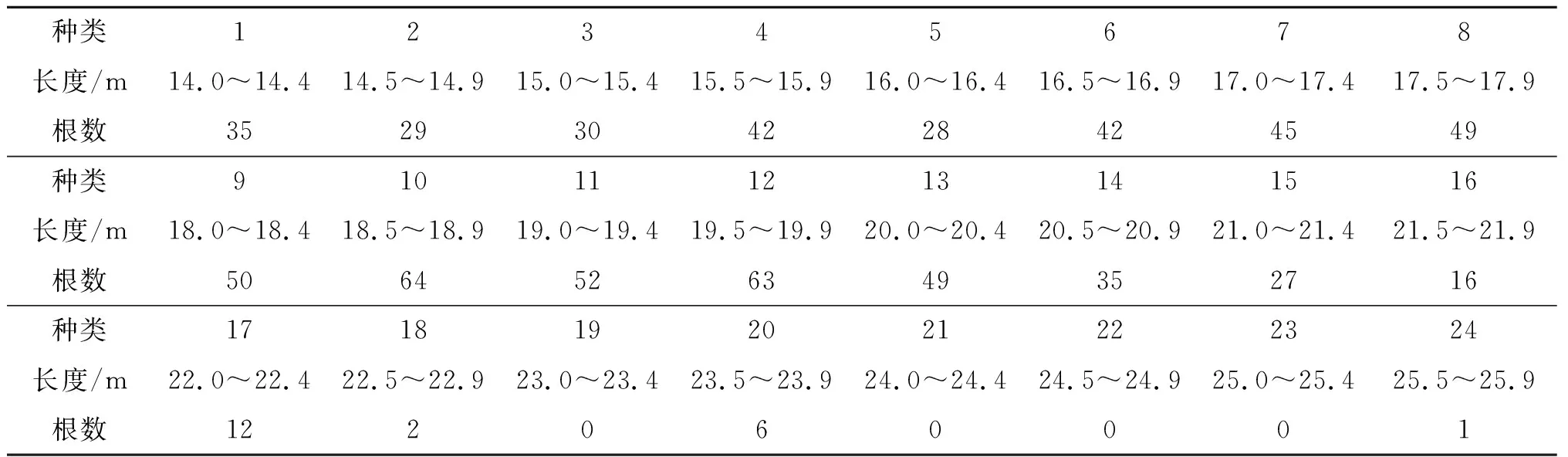
表2 原料描述
公司对搭配方案的要求如下:
1)针对一定量的原料,搭配出的成品捆数越多越好;
2)成品捆数相同的方案,各最短长度最长的成品越多,方案越好;
3)为提高原料利用率,总长度允许误差为±0.5 m,总根数允许比标准少1根。
请建立上述问题的数学模型,并根据表1、表2给出的实际数据进行求解,给出搭配方案。
2 符号说明

表3 符号说明Tab.3 Symbol description
3 模型的建立、求解及改进
以捆数最多为目标函数,成品总长度、成品中原料根数以及每种原料现有总根数为约束条件,建立规划求解模型。
3.1 模型的建立与求解
根据题中所给成品总长度、成品中原料根数的限制及现有原料的总根数,建立整数非线性规划模型Ⅰ[2-3]:
目标函数:maxSi,
利用Lingo软件[4-6]对模型进行求解,得搭配方案1及相应的成品捆数(见表4)及原料剩余量aj(单位:根)(见表5),再将剩余原料根数代入模型Ⅰ中,运用Lingo软件求解,得到搭配方案2及相应的成品捆数(见表6)。多次运用Lingo软件求解,得出原料组成成品的各种搭配方案及各种方案下的成品捆数(见表7)及原料的剩余量(见表8)。

表4 搭配方案1及相应的成品捆数Tab.4 Match Plan 1 and the corresponding bundles of finished products

表5 原料剩余量aj/根Tab.5 Raw material surplus aj/root

表6 搭配方案2及相应的成品捆数

表7 搭配方案及各种方案下的成品捆数
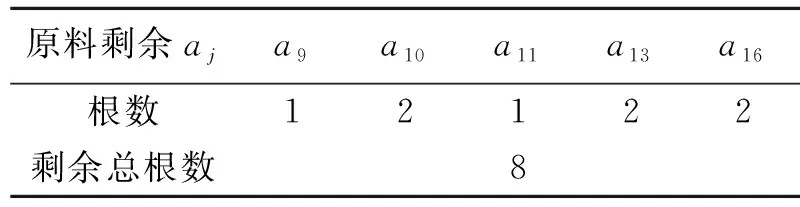
表8 原料剩余量
原料组成的成品总捆数为
从结果可看出,得到的成品数是135捆,比文献[7]中的结果“规格三得到最大捆数为130”要好,较文献[8]中的结果“最多捆数为 134”也要好。原料剩余量仅8根,而且不能配成一捆成品,因此方案可行,结果可靠。但求解时,未考虑题中对搭配方案的要求2),因此提出模型的改进。
3.2 模型的改进
考虑题中对搭配方案的要求2), 对于成品捆数相同的方案,最短长度最长的成品越多,方案越好,因此改进模型时,首先将最短长度原料(14.0~14.4 m的原料)先忽略不算,对其余的原料利用模型Ⅱ求解,得到各种搭配方案、各种方案下成品捆数及不能搭配的剩余原料数;再将最短长度原料(14.0~14.4 m的原料)放入剩余原料中,利用3.1中的模型Ⅰ求解,得到各种搭配方案、各种方案下成品捆数及不能搭配的剩余原料数。
建立整数非线性规划模型Ⅱ:
目标函数:maxSi
利用Lingo软件对模型进行多次求解,所得结果如表9和表10。将表10中数据代入模型Ⅰ,用Lingo软件对模型进行多次求解,所得结果如表11,最终原料剩余量如表12。

表9 忽略最短长度原料的求解结果

表10 原料剩余量

表11 将最短长度原料放入剩余原料后所得结果

表12 模型改进后的最终剩余原料
由表9,表11得原料组成的成品总捆数为
3.3 模型的评价
模型改进前与改进后得到的成品总捆数都是135捆,但是改进前的成品捆中有35捆含最短长度原料(14.0~14.4 m),即最短长度为14.5~14.9 m的成品捆数为100捆,改进后的成品捆中只有18捆含最短长度原料(14.0~14.4 m),即最短长度为14.5~14.9 m的成品捆数为117捆,可见改进后的模型更符合题目要求。该问题的模型简单易懂,利用Lingo软件求解方便快捷,结果正确合理。
