施行以点带面 彰显核心素养——《方程的根和函数的零点》教学设计

牟小兰

（重庆市万州第三中学 重庆万州 404000）

一、教材分析

以人教版《普通高中课程标准实验教科书》A版数学必修一为蓝本，分析第三章《函数的应用第一节《函数与方程》的第一课时《方程的根与函数的零点》的教学内容。本节课主要内容是函数零点定义、函数零点与相应方程根的关系、函数零点存在性定理，是一节概念课。本节课不仅为二分法的学习做准备，也为方程与函数提供了连接点，从而揭示两者之间的本质关系，这种联系正是“函数与方程思想”的理论基础，为今后进一步学习函数与不等式等其他知识联系奠定了坚实的基础，一步一步地形成学生的数学素养，为今后适应社会做准备。

二、学情分析

学生已经了解一些基本初等函数的模型，具备一定的看图识图能力，这位本节课利用函数的图象，判断方程根的存在性提供了一定的知识基础。但高一学生对数形结合与抽象思维尚不能完全驾驭。因此，函数与方程相联系的观点的建立，函数应用意识的初步树立，是本节课必须承载的任务。

三、教学目标

知识与技能 理解函数零点的定义及方程的根与函数零点之间的联系；理解函数零点存在性定理；能利用函数的图象和性质判断函数的零点个数及所在区间。

过程与方法 渗透由特殊到一般的认知规律，提升学生的抽象和概括能力，领会数形结合、函数与方程等数学思想。

情感、态度与价值观 认识函数零点的价值，使学生认识到学有所用；培养学生认真、耐心、严谨的数学品质；让学生在自我解决问题的过程中体验成功的喜悦。

四、教学重难点

重点：理解函数零点的定义，体会方程的根与函数零点之间的联系，掌握函数零点存在性的判断。

难点：在合情推理中让学生掌握体会判定定理，并能初步应用。

五、教学方法

自主学习，合作探究，讲练结合

六、教学过程

（一）课题引入（2分钟）

某网店经营的暖手袋原价x元，在某天推出五折优惠和免邮费的促销活动，以提高本店的销售额度。小李同学利用支付宝里的50元在促销期间购买此暖手袋后余额为y元。

①请帮助小李同学建立以x为自变量，y为函数的关系式（暂不考虑定义域）。

②原价为多少元时余额为0？

以非常简单网购话题出发，引起学生注意，探索数学问题，激发学习兴趣。

（二）自主学习（12分钟）

引例中方程x-50=0的实根50，就是函数y=x-50的零点，所以，我们由特殊到一般，得出函数零点的定义：

对于函数y=f(x)，我们把使f(x)=0的实数叫做函数y=f(x)的零点。

理解定义，提出问题：方程的根与相应函数的零点之间有什么联系？

为了更好理解定义，回答该问题，我们应像涓涓细流般慢慢地将知识浸润于学生的心田，选用学生已知熟悉的知识来理解改知识和探究未知。

（三）组织探究（11分钟）

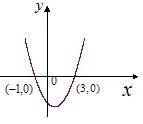
结合函数y=x2-2x-3的图象观察发现：

①在区间[-2，1]上有零点：

f(-2)=5,f(1)=-4,f(-2)·f(1)＜0

②在区间[2，4]上呢？

运用特殊到一般的学习规律，得出函数零点的存在性定理。

（四）练习反馈（5分钟）

①函数y=x2-3x+2的零点是（ ）

A.（1，0），（2，0） B.x=1 C.x=2 D.1，2

②函数f(x)=2x-3零点所在的一个区间是（ ）

A.（-1，1） B.（0，1） C.（1，2） D.（2，3）

以上练习是基础性练习，意在检验学生掌握基础知识的情况。先请学生作答，并请一位学生作为“小老师”为大家做简单讲解后，教师再稍作点评。

（五）协作交流（8分钟）

为了进一步运用该知识解决函数的零点问题，我们一起来看看这道例题。

例：函数f(x)=1nx+2x-6有没有零点？有几个零点？

分析：

①利用函数零点的存在性定理，借助计算器或计算机作出x，f(x) 的对应值表和图像。

②图象法：函数y=f(x)图象连续，f(a)·f(b)＜0，且f(x)为单调函数，则y=f(x)有且只有一个零点。

③数形结合法：函数f(x)=1nx+2x-6的零点问题，转化为方程1nx+2x-6=0即1nx=6-2x的实根问题，有转化为函数y=1nx和y=6-2x的交点个数问题。

（六）课堂小结（2分钟）

①基础知识：函数零点的定义；函数的零点存在性定理；确定函数零点的方法。

②思想方法：特殊到一般，数形结合，转化与化归，函数与方程

③责任担当：面对困难，勇于探索，精准探究，实现梦想

（七）板书设计

（八）课后巩固

①P88 练习1

②思考题：怎样求出函数 的零点的近似值。

③阅读P91《中外历史上的方程求解》，了解方程的发展历程。

（九）课后反思

本节内容以函数图象为主要载体，通过本节课的学习研究，使学生从“数”“形”两个层次理解函数零点的定义，突出“数形结合”的数学思想。在实施教学过程中指导学生学习方法，注重数形结合、转化与化归、函数与方程等数学思想的渗透，是学生对知识的掌握不仅仅停留在表面，还在更深层次的问题是思考，使数学核心素养的培养得到落实。

总之，我们要准确把握学生的认知规律，努力做到不断完善每节课，思路流畅，层次分明，问题引领，关注思维，让学生在学习中参与其中，不断提高自身的数学素养。