面向基于Voronoi结构的随机多孔骨植入材料的小孔结构参数化建模方法研究

谢焯俊 方辉 沈显峰 党永坤

近年来，增材制造技术的逐渐成熟使复杂多孔骨植入物的研究发展迅速。此类多孔植入物有效地避免了“应力遮挡”效应，并改善了植入物与原生骨组织的结合效果。而对于应该采用什么样的多孔结构才更有利于成骨细胞长入的问题，也渐渐受到了人们的重视[1-6]。相关研究表明，与松质骨组织相似的多孔结构可为成骨细胞提供一个与自然松质骨相似的生物环境，其均匀的内部体液流场与较柔顺的结构刚度可为成骨细胞的长入创造有利条件[2,7-8]。

基于Voronoi 结构创建的仿生随机多孔支架模拟了松质骨组织的多孔结构，从而具备了较好的骨长入性能，是一种较为独特的骨植入材料[3-5,7,9]。Gómez[7]和Fantini 等[1,10]基于建模软件Rhinoceros 及其插件Grasshopper，设计了一个随机多孔模型的建模程序。然而该建模程序无法准确控制小孔结构参数，不利于对模型进行进一步的生物力学性能和骨长入特性的研究。为构建出具有准确孔径、孔隙率的Voronoi多孔模型，以便对其孔隙参数开展优化研究，提高其生物力学性能与骨长入性能，本文在Gómez 等的研究基础上加以完善，引入了Voronoi 细胞密度和Voronoi 细胞收缩系数两个建模参数，设计了一系列的小孔结构参数测量程序。通过几何关系和析因实验获得了平均孔径和孔隙率与所对应的和之间的数学模型，实现了对小孔结构参数的准确控制。最后，测量了由SLM 工艺制备的316 L 样件的小孔结构参数，验证了该方法的有效性。

1 材料与方法

1.1 随机多孔模型的参数化建模

1.1.1 随机多孔模型的创建

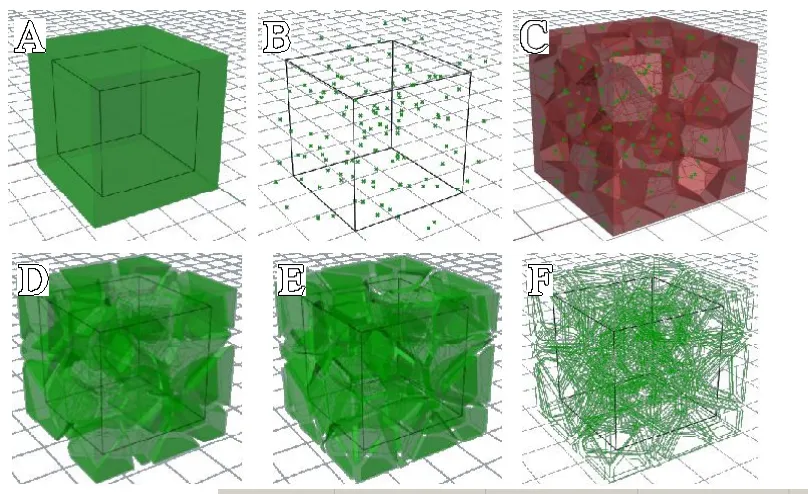
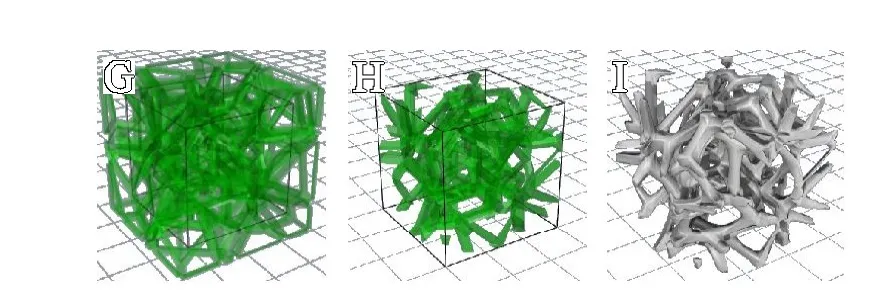
图1 随机多孔模型的创建流程（黑色线框为原实体模型边框）:A.创建建模空间；B.创建随机点阵；C.生成3D Voronoi 结构；D.收缩细胞；E.收缩细胞壁；F.提取收缩后的细胞及细胞壁的棱边；G.连接相邻棱边端点创建曲面；H.与原实体模型求交；I.网格圆滑处理

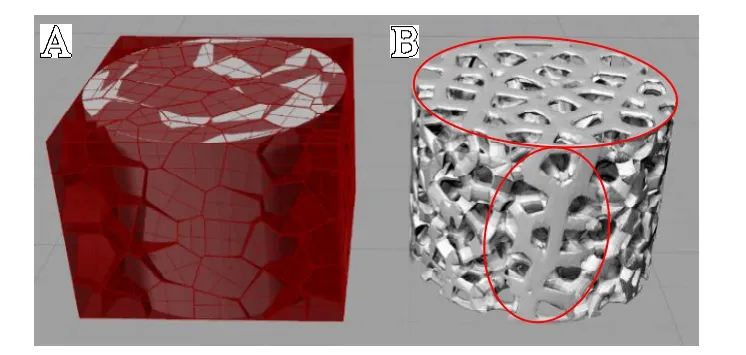
图2 不膨胀建模区域对建模效果的影响:A.在未经膨胀的建模区域内创建的Voronoi 结构； B. 由此创建出的圆柱多孔模型上出现的局部壁面结构（红圈）创建比模型边界更大的建模区域是为了消除非矩形模型表面出现如红圈内所示的局部壁面结构，保证孔隙结构的一致性

接着在建模区域内采用随机点生成器Populate 3D 生成个随机点，即可得到覆盖整个外形模型的随机点阵（见图1B）。再调用Voronoi 3D 模块，即可得到由多个Voronoi细胞（以下简称细胞）构成的类似闭孔泡沫的3D Voronoi 结构（见图1C）。此时，调用炸开（Explode）模块拆分3D Voronoi 结构的几何特征，再以各个细胞的重心以及各个多边形细胞壁的重心为中心，分别缩小细胞（见图1D）和细胞壁（见图1E）为原尺寸的倍（这是一个长度的缩放系数）。再次调用炸开模块，进一步拆分收缩后的细胞和细胞壁，提取其棱边特征，得到由一系列两两平行的棱边构成的框架（见图1F）。提取这些棱边的端点，通过组合命令将两两平行的棱边上的4个端点合为一组，并以每组端点为参考点创建网格面片，合并所有面片就得到了由平面面片组成的随机多孔结构（见图1G）。通过对原实体模型和多孔结构进行网格求交操作，就能得到具有原实体模型外形的随机多孔模型（见图1H）。最后调用Weaver Bird 网格处理组件对模型进行圆滑处理，便完成了如图1I 所示的具有圆滑小梁结构的随机多孔模型的创建。

图3 创建随机多孔模型的Grasshopper 主程序电池图

图3 展示了上述建模流程的电池图。通过选用不同的实体模型，设置不同的和该程序就能自动创建出具有不同外形、孔径和孔隙率的随机多孔模型，具有很高的灵活性。

1.1.2 小孔结构的参数化设计

1.1.2.1 小孔结构参数的定义与测量

平均孔径方面，Fantini 等[1]使用了与形成各个小孔的细胞体积相等的球体的直径来表征孔径，在此称之为“等体积球法”。易知，收缩后的细胞体积（式2）为:

根据球体体积公式可推导出等体积球的直径，也就是对应的平均孔径方程（式3）:

然而，本文在沿用上述方法的过程中发现，建模过程中的圆滑处理会使小梁截面尺寸缩小，导致实际孔径变大，而通过该方式表征的孔径偏小。该现象在创建孔隙率小于80%的泡沫模型时尤为明显。

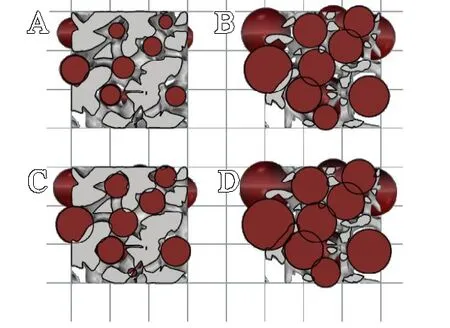
图4 不同测径法的孔径拟合效果:A.等体积球拟合=50%模型；B.等体积球拟合=88%模型；C.等效体积球拟合=50%模型；D.等效体积球拟合=88%模型

鉴于等效体积球法可获得更贴合小孔内壁的拟合球，本文认为通过该方式表征的平均孔径更为合理，其对应的孔径方程（式4）为:

孔隙率测量方面，可以很方便地使用Grasshopper 中的体积测量组件来实现，其测量公式（式5）为:

小梁直径方面，如图5 所示，Voronoi 随机多孔结构中大部分小梁都是由邻近的3个细胞围绕而成的，可将其截面近似为一个等边三角形。本文以该等边三角形的外接圆直径来表征小梁直径，其计算公式（式6）为:

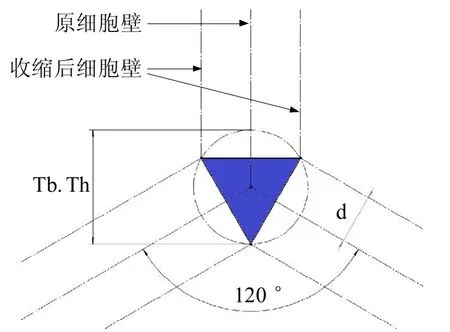
图5 平均小梁直径的计算模型

1.1.2.2 建模参数推导

通过变换“等效体积球法”的孔径方程（式4），能够很方便地推导出有关细胞密度的方程，即:

表1 关于与和 的二水平析因实验

表1 关于与和 的二水平析因实验

序号（%）11500 0.56 57.7images/BZ_9_1546_2821_1567_2846.pngc（个 mL-1）images/BZ_9_1889_2812_1911_2839.png images/BZ_9_2081_2813_2106_2839.png2 43000 0.56 57.131500 0.85 91.84 43000 0.85 90.9

其一阶回归模型如式8 所示，方差分析结果表明该模型的置信度高达99.97%，可以认为是合理的。

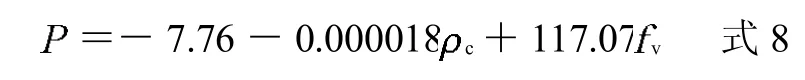
联立式8 和式7 两个方程，即可求解出fv的设计计算公式:

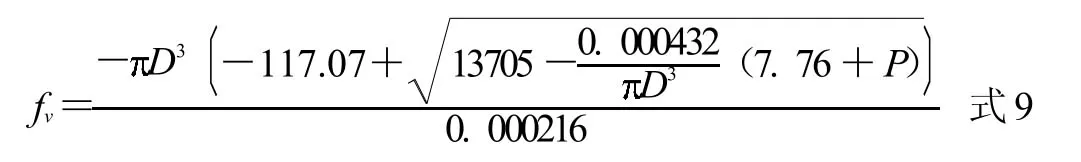
最终，本文通过设计Grasshopper 程序实现了上述小孔结构的参数化设计与随机多孔模型的参数化建模。如图6 所示，只需要输入多孔模型的目标孔径目标孔隙率，并导入原实体模型，程序将自动完成随机多孔模型的创建，以及平均小梁直径和实际孔隙率的测量。

图6 随机多孔模型参数化建模程序的输入输出面板

1.2 随机多孔样件的SLM 制备

1.2.1 实验模型的创建

使用本文设计的建模程序创建了一系列直径8 mm，高10 mm，具有不同组合的圆柱状随机多孔模型，具体参数见表2。

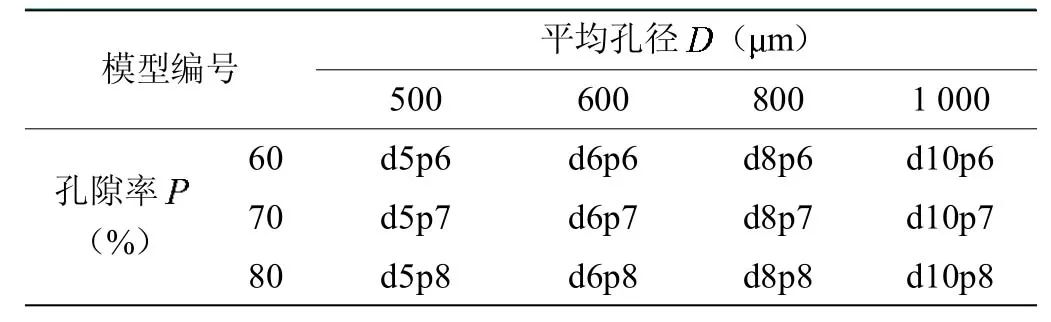
表2 随机多孔样件模型小孔结构参数

对于SLM 增材制造工艺而言，设备的最小成形尺寸（可成形的最小特征的尺寸）在很大程度上决定了多孔模型能否成功制备。为探讨样件的成形效果和模型平均小梁直径之间的关系，本文对各个样件模型的平均小梁直径进行了测量，测量结果如图7 所示。

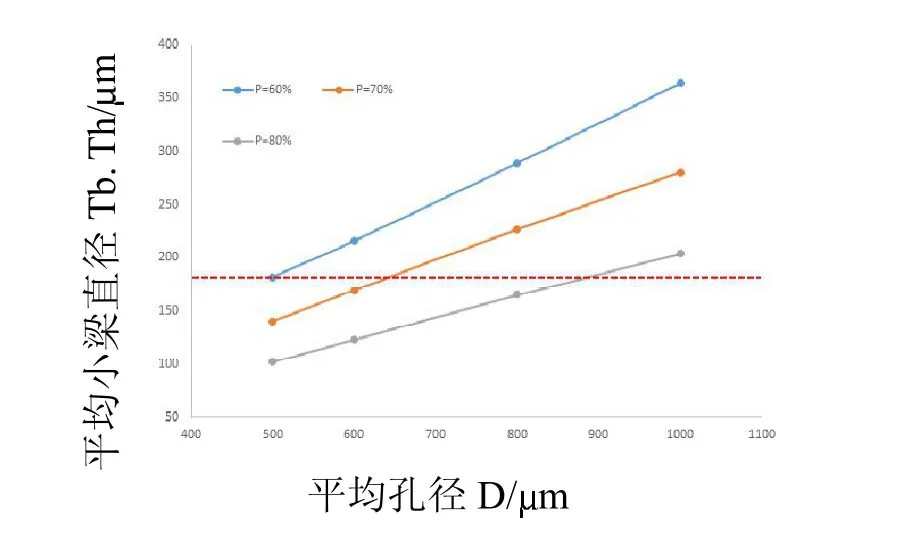
图7 不同-模型的平均小梁直径变化

可见该系列模型中平均小梁直径为102 ～364 m，小梁直径最小的模型为d5p8，而最大的为d10p6。随着孔径的增大和孔隙率的降低，小梁直径将增大，且孔径和孔隙率对小梁直径的影响均呈现线性关系。

1.2.2 实验材料

实验使用的316L 不锈钢粉末组成成分见表3。采用激光衍射仪粒度分析仪测得的粉末粒度分布，其中值粒径为36.63 m，对于本实验而言是合适的。

1.2.3 SLM 工艺参数设置

实验使用的SLM 设备其额定激光功率400 W，激光光斑直径约75 m。成形厚度设置为40 m，激光束采用轮廓（Contour）扫描策略，成形舱内充入氮气作为保护气。在轮廓扫描策略中，轮廓光斑补偿（contour offset）决定了激光光斑的中心轨迹对于模型截面轮廓线向模型实体内偏移的距离，通常设置为与熔池半径相等。如图8 所示，亮蓝色粗线为模型的截面轮廓，而带箭头的深蓝色细线就是激光光斑中心的扫描轨迹。图中的三个扫描路径由内而外分别对应了0 m、50 m 和100 m 三种光斑补偿。

表3 316 L 不锈钢粉末成分

表4 SLM 轮廓扫描工艺参数

根据经验，本文设置了如表4 所示的轮廓扫描工艺参数。

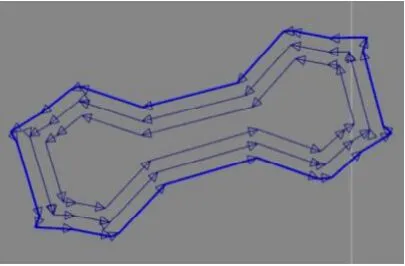
图8 带不同光斑补偿的光斑中心轨迹

2 结果

本次实验成功制备了编号为d5p6、d6p6、d8p6、d8p7、d10p6、d10p7、d10p8 的7个不锈钢多孔样件，其余5个模型的样件均无法成形。通过机械振动与超声波清洗清除了样件内部的残留粉末后，对比图9 与图10 可见，实际样件的宏观形貌与对应模型外观较为吻合。利用光学显微镜观察样件的孔隙形貌，如图11 所示，样件在微观上呈现出了较为明显的Voronoi 随机孔隙结构。

图9 部分模型的小孔形貌对比，从左到右分别为:d6p6、d8p6、d10p6、d10p7、d10p8 模型

图10 部分成功制备的316L 不锈钢泡沫，从左到右分别为: d6p6、d8p6、d10p6、d10p7、d10p8 样件

图11 d8p6 样件的表面孔隙形貌:A.×50 倍；B.×150 倍

用排水法测定样件孔隙率，测量结果见表5。

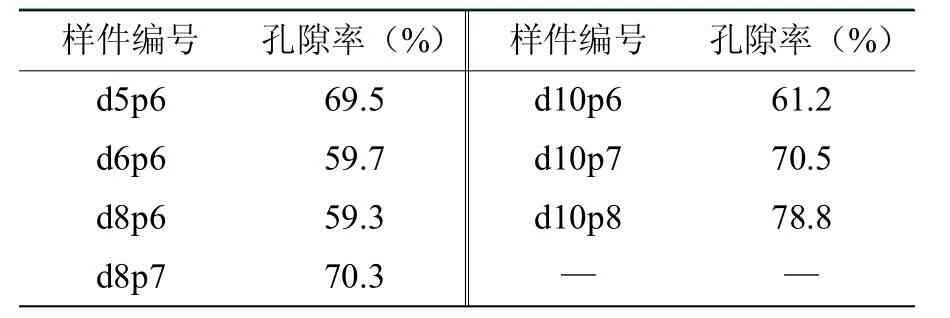
表5 多孔样件的孔隙率测量结果

将样件从中部切开，并将切口磨平、抛光，使用光学显微镜观察其横截面孔隙形貌。如图12 所示，可见三维模型与其实际样件的孔隙形貌基本一致，均表现为多个小孔连通成片的孔隙结构，样件成形质量较好。

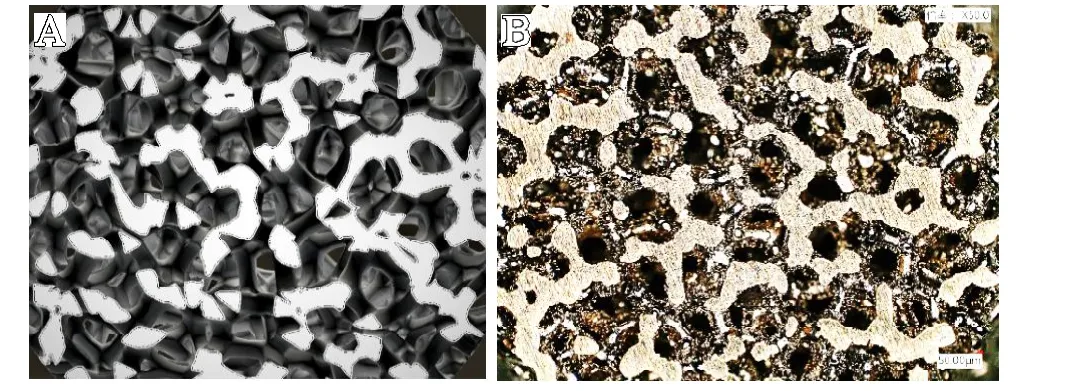
图12 d8p7 样件与模型的截面孔隙形貌（高亮区域为小梁截面）:A.模型截面；B.样件截面

通过统计样件截面内大孔的平均孔径来粗略地测量样件的平均孔径，测量结果见表6。

表6 多孔样件的平均孔径测量结果

3 讨论

本文提出了“等效体积球法”用于拟合Voronoi 随机多孔模型的小孔孔径，研究了相关建模参数与多孔模型参数之间的数学关系，并在此基础上设计了参数化建模程序，实现了Voronoi 随机多孔模型的参数化建模。

随后，从SLM 成形质量与模型小孔结构参数所呈现出的关系中可以发现，模型的小梁直径很大程度上决定了其样件的成形质量。小梁直径范围在182 ～364 m 的样件成功成形，然而其中小梁直径分别为182 m 和204 m 的d5p6、d10p8 样件强度较低，小梁易断裂。其原因在于，其平均小梁直径已接近本实验工艺的光斑补偿下设备所能识别的最小特征尺寸（即2 倍的光斑补偿，此处为200 m），以至于部分小梁轮廓未被切片程序完整识别，因而在SLM 过程中激光未能扫描到位而熔合不佳。同理，小梁直径小于182 m的模型也则均未能成形（图7 中红色虚线以下的模型）。

孔隙参数方面，各个样件的孔隙率和平均孔径与设计孔径基本吻合，但由于d5p6 和d10p8 样件的成形质量较差，表面缺失小梁较多，出现了模型上不存在的大孔隙，导致其孔隙率偏高且孔径偏差较大。而其余样件的结构完整，孔隙率的绝对误差均控制在了±1.2%以内，而平均孔径的相对误差基本都控制在了8%以内。可见，在保证成形质量的前提下，本文提出的设计方法能够实现对此类多孔结构平均孔径和孔隙率的准确控制，可为该类多孔植入物的生物力学研究与骨长入研究提供具有精准小孔结构参数的样件，还为进一步设计出具有梯度孔径、梯度渗透性、梯度力学性能等特性的多孔植入物提供了一定的理论基础。

此外，在研究过程中笔者还总结出了以下几个要点。

（2）多孔模型的数据量主要由孔的数量决定，模型孔径越小、孔隙率越大、外形体积越大，小孔的数量就越多，则模型的数据量和建模时耗都将急剧增大，以至于在需要创建大尺寸、多孔植入物模型时，或将对计算机的性能提出过高的要求。

（3）根据设备在一定工艺参数下的熔池直径来合理地设置光斑补偿对此类多孔样件的SLM 制备具有至关重要的影响。熔池直径越小，可设置的光斑补偿越低，可制备出的小梁直径越小、精度越高，从而可制备的多孔样件参数范围也越大。但是，熔池直径同时受到激光功率、光斑能量分布、扫描速度、原材料类型及其粉末粒度等因素的交互影响，还需要针对不同的材料开展更多的工艺试验，以尽可能地缩小熔池直径。

大量多孔植入物骨长入特性的研究表明，最适合成骨细胞和血管长入的小孔直径为400 ～500 m，而孔隙率要求更是高达90%。较高的孔隙率可使得多孔材料的弹性模量与原生骨相近，同时还具有更高的液体渗透性，在提高植入物的生物力学相容性的同时，体液的流动还能为植入物内的成骨细胞提供充足的养分和氧气，对伤患处的快速愈合具有促进作用。然而，受限于当前工艺参数下SLM 设备较大的熔池直径，笔者只能制备出平均小梁直径≥182 m 的随机多孔样件（对应孔隙参数为=500 m，=60%）。可见其对于骨植入而言还不甚理想，孔隙率有望进一步提高。因此，接下来的研究工作应关注于此类多孔结构的SLM 工艺，以获得尽可能小的熔池直径，扩大可成形孔隙参数的范围，进而拓展参数化建模方法与SLM 工艺在设计制备高性能多孔植入物方面更多的可能性。

感谢四川大学青岛研究院对本研究的资助。