基于统计学模型的CBTC系统ATO停车精度自适应优化算法

谭力天，陈 昕，李澎东，田昌宇

(湖南中车时代通信信号有限公司，长沙 410005)

基于通信的列车运行控制系统（CBTC）中，列车自动驾驶功能（Automatic Train Operation，ATO）停车精度是系统性能的重要指标，它直接影响乘客上下车，甚至影响整个CBTC系统的运行效率。由于列车长时间不间断运行，载客人数不断变化，各个车辆特性存在差异，使得列车精确停车受到较多干扰而存在不确定性。为了保证列车运行过程中一定的停车精度，列车自动驾驶控制方法有PID控制算法[1]，模糊控制算法[2-4]，自适应控制算法[5-6]。PID控制算法需要根据控制情况调节算法参数，并且参数确定后不易修改，针对多列车的参数修改工作繁杂，停车精度稳定性较差。模糊控制算法学习能力较强，离线学习有较大优势可以有效调节算法参数，但是算法实时性有所欠缺。自适应控制算法可以对不确定性进行在线修正，较好的解决系统不确定性造成的不利影响，但是当前的自适应算法需要建立适当的精确模型，模型选择对停车精度影响较大。

本文利用自适应控制算法的优势，在确保对不确定性修正和稳定性要求的前提下，采用马尔可夫统计学模型降低了对精确建模的要求，提出具有更广泛适用性的基于统计学的ATO停车精度自适应优化控制算法。

1 列车精确停车模型

1.1 列车停车精度因素

影响列车的停车精度因素有：线路信息、列车阻力，车辆特性，列车重量、应答器位置校正、列车空转打滑，列车施加加速度。

1）线路信息和列车阻力随着线路和车辆情况确定后可以获得较为准确的计算值。以上两种因素属于可计算因素。

2）列车作用力的作用时间因为车辆特性不同存在差异。列车停车过程中，从命令下达到牵引切除时长t1；从牵引切除到制动装置开始作用时长t2；从制动装置开始作用到制动装置施加有效的制动力时长t3。施加有效制动力的时长为t=t1+t2+t3，总时长t各车辆存在差异，该时间差异对于列车精确停车存在影响。该因素属于单个车辆因素。

3）车辆载客人数动态变化造成列车重量存在差异。应答器位置校正根据列车实际运行情况每次校正位置存在差异。列车空转打滑对位置计算影响较大属于特殊情况，出现空转打滑干扰时停车精度较差。以上3种因素都属于不确定干扰因素。

4）列车施加加速度计算存在偏差，这使得最终ATO停车位置会不同。该因素属于算法偏差因素。

1.2 ATO精确停车制动控制方法

影响列车的停车精度因素综合作用于列车，表现为列车的速度变化，以列车到停车点的距离和列车速度为特征量表征列车的停车精度。

如图1所示，在列车停车过程中，根据列车的实时速度和停车点位置，计算速度—位置曲线。在这个过程中控制算法有PID控制、模糊控制、自适应控制。

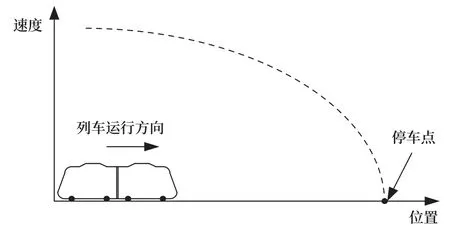
图1 列车速度-位置曲线Fig.1 Train speed-position curve

PID控制通过调节比例、积分、微分3个参数控制列车实际速度。

模糊控制：以模糊数学理论建立模糊规则，以模糊推理进行控制，将系统参数通过该规则进行映射推理，以PID控制为例，以单点和三角形模糊集合方法尺度变换转化参数论域范围，得到模糊化的参数，△kp、△Ti、△Td。该规则可以根据实际情况进行调整。

其中△p、△i、△d表示模糊控制修正的部分。

自适应控制：以模型参考自适应控制为例，构建与实际系统具有相同特性的参考模型，以两个系统的误差函数作为性能指标，调节系统参数。构建参考模型：

定义误差函数：

以e表征控制系统性能，调节控制系统参数。

2 统计学模型

统计学马尔可夫模型自20世纪80年代开始，陆续成功地应用于语音识别、机器翻译、拼写纠错、图像处理、基因序列分析等多个领域[7-10]。统计学模型与样本数据等强相关，随着地铁运营里程的增加，系统会趋于稳定，样本的可用性和可信度会逐渐增强，采用拟合的方式对统计学概率进行平滑。

2.1 N元马尔可夫模型

假定列车的停车精度为S，认为该精度值是由w1，w2，……，wn共n个事件影响，该精度出现的概率是P(S)，则P(S)可以表示为：

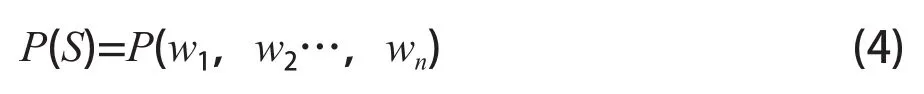
将该条件按照条件概率公式展开则有：

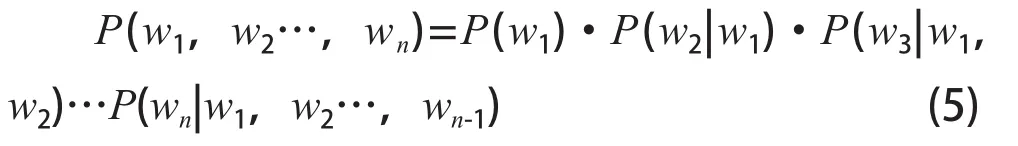
其中P(w1)表示第一个事件的概率；P(w2|w1)是在已知第一个事件的条件下第二个事件的概率；P(wn|w1，w2…，wn-1)表示在已知前n-1个事件的条件下wn的概率。

为了解决3个及3个以上事件的条件概率P(w3|w1，w2)计算的复杂性俄国科学家马尔可夫提出简化模型。假设任意事件wi的条件概率只同其前一个事件wi-1有关，于是P(S)可以表示为：

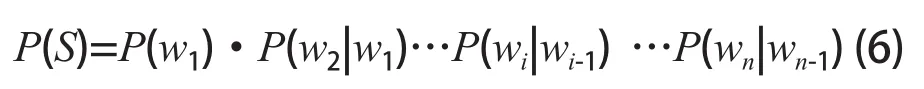
任意事件wi的条件概率与其前i-1个事件相关的模型称为N元模型，理论上N越大模型越精确。但是由于N元模型的复杂度是呈指数增长，考虑到实时性和空间成本，本文采用二元模型。

2.2 模型的训练方法

根据大数定理以采样数据观察结果作为统计学概率计算基础。根据运营要求列车停车精度±30～±50 cm内，这使得现场运营结果不一定存在停车精度超过±50 cm，但是从概率上不能认为这种情况不会发生。类似的为了避免在统计过程中没有出现的停车精度概率为0情况。首先保证训练用数据样本的数量充足，停车精度覆盖范围尽可能的全面覆盖。其次采用卡茨退避法处理零概率问题。

其中，Num是统计频次，T是阈值，统计频次不小于阈值认为概率估计就是相对频度，f()是统计学相对频度，fg()是统计学采用古德—图灵估计后的相对频度，Q(wi-1)是估计补偿相对频度。需要保证下式成立：

3 统计学模型对停车精度的优化

为解决列车精确停车算法与车辆特性问题，采用统计学模型对列车精确停车进行自适应优化。

3.1 停车精度二元马尔可夫模型

考虑以下3种类型停车精度概率情况，一列车上一站台停车精度，二列车同一站台上次停车精度，三列车同一站台昨天同一时间停车精度。主要从可计算因素、车辆因素、不确定干扰因素、算法偏差因素考虑对本次停车精度的影响。列车上一站台停车精度概率情况，特别考虑最近一次停车误差对本次停车精度的影响。

3.2 模型的训练

列车的进站停车过程部分数据统计如图2所示。

图2中共有32组统计数据；其中纵坐标为列车目标距离（cm），表示列车与停车点的距离，最终的值为停车精度；横坐标为时间（ms），表示到列车停车的时间周期间隔。训练数据样本数为2 840组，随机选择其中的75%为训练数据。在剩余的25%样本中随机选择了10%得到列车停车精度统计如图3所示。

通过统计分析，采用古德—图灵估计对停车精度概率分布进行曲线拟合如图4所示，消除零概率并使得概率分布平滑。

图2 列车进站停车数据统计分布Fig.2 Statistical distribution of train approach stopping data

图3 停车精度统计Fig.3 Statistics for stopping accuracy

4 仿真分析

通过3.1中3种不同类型概率统计情况，通过对ATO停车模型进行优化，分别获得停车精度统计。对应的列车进站停车数据统计分布如图5～7所示。

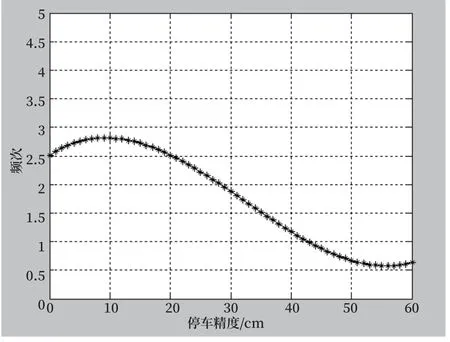
图4 停车精度概率分布拟合曲线Fig.4 Fitting curve for the distribution of stopping accuracy probability

采用期望和方差指标评价停车精度，如表1所示。

表1 停车精度比较Tab.1 Comparison of stopping accuracy

图5 类型一列车进站停车数据统计分布Fig.5 Type 1 Statistical distribution of train approach stopping data

图6 类型二列车进站停车数据统计分布Fig.6 Type 2 Statistical distribution of train approach stopping data

样本中包含了因为空转轮滑引起的53 cm停车精度等数据，其期望值和方差较大。优化后可以看到类型一考虑列车上一站台停车精度，期望较样本数据降低，但是比类型二和类型三要大；方差值比样本数据和类型三低，但是高于类型二。类型二考虑列车同一站台上次停车精度，期望比样本数据和类型一要低，比类型三要高；具有最小的方差值。类型三考虑列车同一站台昨天同一时间停车精度。具有最小的期望值；方差值小于样本但是比类型一和二要大。

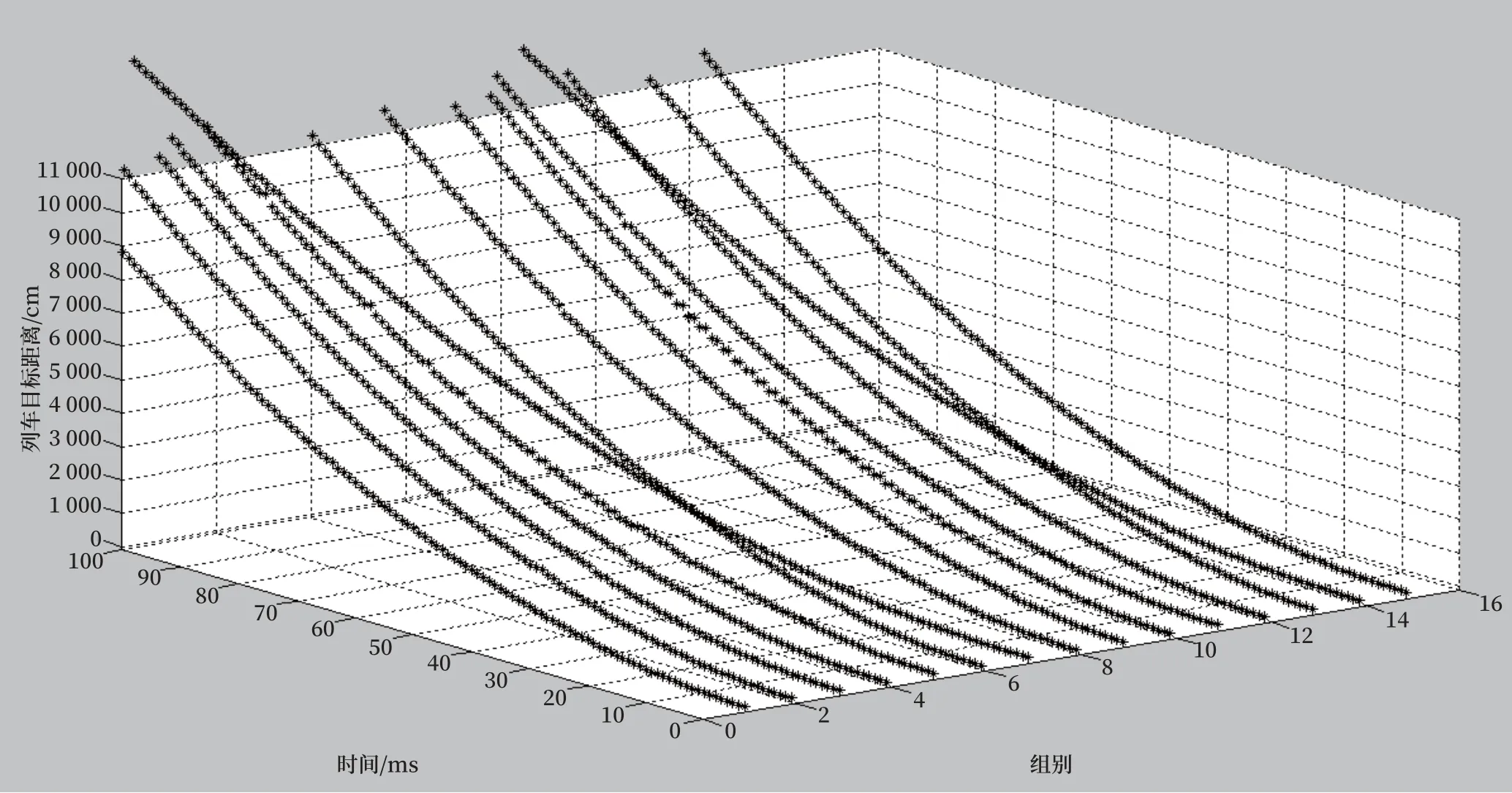
图7 类型三列车进站停车数据统计分布Fig.7 Type 3 Statistical distribution of train approach stopping data

优化之后模型的停车精度较样本有一定改善，类型三具有最优的期望，类型二具有最小的方差。

5 结语

设计一种基于统计学马尔可夫模型的CBTC系统ATO精确停车自适应优化方法。以统计列车停车过程数据，采用古德—图灵估计拟合出停车精度概率分布曲线，从而对列车停车过程进行自适应参数优化。采用优化模型获得3种不同类型的情景概率统计，并得到相应的停车精度数据。采用期望和方差作为停车精度评价指标，将样本、类型一、类型二、类型三数据停车精度指标进行对比，优化模型对ATO停车精度有一定改善，仿真结果表明获得了理想的停车精度。