我形我数，凸显本质——几何直观在培养数学思维中的价值窥探

江苏省常熟市商城小学 邵月芳

小学阶段，学生的思维处于具体形象思维向抽象思维过渡的重要阶段，但形象思维仍占主导地位。在现行修订的苏教版教材中，我们也不难发现，各种实物图、各式图形及简约符号等随处可见，直观性强成为本套教材的一大亮点。“形”与“数”形影不离，成为数学的两块大基石。再来看看《义务教育数学课程标准（2011 年版）》，几何直观作为十大核心概念之一，充分体现了几何直观的价值。在教学中，教师应该充分利用几何直观的优势，通过想象、推理、比较等培养学生空间想象能力，直觉洞察能力，和主动使用图形的意识和习惯，从而提高问题探究的兴趣，有效理解概念本质，加强数量关系的内化，促进学生数学思维水平的提升。

一、善用几何直观发挥想象，精心预设提高研究兴趣

爱因斯坦说过：“想象力比知识更重要，因为知识是有限的，想象力概括着世界上的一切，推动着进步，并且它是进化的源泉。严格地说，想象力是科学研究中的实在因素。”通过直观的图形开展想象，可以大大提高学生研究问题的兴趣。

在进行六年级“平面图形总复习”一课的教学时，我设计了“回忆再现来温故”“系统梳理悟转化”“应用拓展促知新”和“反思总结谈收获”四个复习板块。在第二板块中，为了加深对转化思想魅力的体悟，我讲述了从前一个部落只有梯形面积计算公式的故事情境，启发学生思考如何求其他图形的面积。我还借助几何画板出示一个可以动态拉动的梯形，让学生发挥想象。随后通过动态演示，直观获得变化形成的三角形、平行四边形、长方形。之后，我又引导学生根据梯形面积公式逐一得到这三种图形的面积计算方法。学生从中体会到了这种“特殊的转化”的奇特之处。在这个故事结束时，我又巧妙地抛出了这样的问题：“此时，你对梯形面积公式有什么新的认识？你想对梯形说什么？”学生此时不禁说出：“太神奇了，这样看来，我们之前的平面图形面积之间的关系图不是可以改一改了，改成用梯形推导出其他图形的面积。”

穿梭于图形和文字之间，几何直观发挥着重要的作用。老师应该利用图形引导学生进行数学思考、想象，并获得数学结论或新的猜测。

接着“平面图形总复习”一课的教学，在“应用拓展促知新”板块中，我又一次借助几何直观的魅力，让孩子们进行大胆猜测，发挥想象，将转化思想推到了新的高度。我设计了如下求椭圆面积的问题。

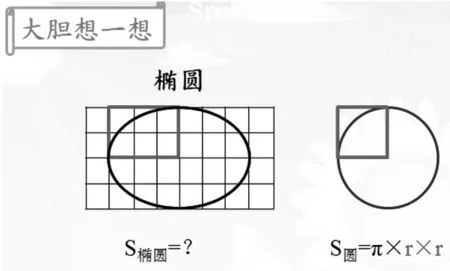
这个问题看似有拔高要求之嫌疑，但是我想说，本课教学目标的达成，很大程度是要看学生对“转化”经验的自觉调用和自我提升。实际教学中，当我提出“你有办法求出椭圆的面积吗？”这个问题后，一部分学生很自然地就想到数格子的方法，也有一部分学生提出要转化来求，但思维受到一定阻碍，没法实现成功转化。此时，我有意识地引导学生联想：“椭圆的面积计算，你觉得可能和哪个图形的面积计算最相似？”学生自然联想到圆形。我继续引导学生观察：“圆的面积公式中半径的平方表示什么？”唤起学生对圆中半径为边长的正方形的再现，从而归纳出：其实圆的面积是这个正方形面积的π 倍。顺势，我就引导学生联想：“椭圆中是不是也有这样相似的情况呢？”当场，就有一个男孩子兴奋地说出了他的大胆猜测，这是学生经历的第二次“思维风暴”。此时，“转化”思想或者说经验已经深入学生内心，很多孩子品尝到了转化的甜头，我的设计也因此顺利达到了预设的目标。

二、巧借几何直观展开推理，多向联系活化概念理解

数学教学的核心是促进学生思维的发展。教学中，教师要全面通过几何直观的数学思维过程，启迪和发展学生思维。而在小学数学教学体系中，概念教学作为数学知识体系的基本构成单位，是“四基”教学的核心内容，是进行逻辑思维的第一要素。为此，在概念教学中，尝试通过展开推理，借助已有直观经验，可以帮助活化概念本质的理解。

例如教学“认识负数”时，在综合练习部分，通过设计“我来当裁判”的实际运用，来考查学生对负数这一概念本质的理解。

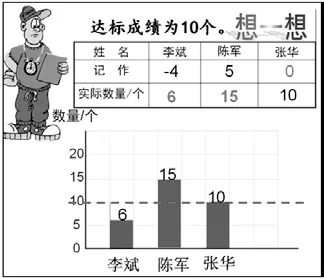
师：学校对四年级男生进行了双飞跳绳测试，达标成绩为10 个。（出示统计图，依次出示几位同学成绩的记录。）

师：李斌的成绩记作-4。你觉得他达标了吗？

生：没有。

师：为什么？

生：因为他比达标成绩少了4 个。（结合学生回答条形图演示比达标个数少4 个）

师：那陈军达标了吗?（教师指着表格中的5 问，此时意见不统一，举手表决）

师：现在出现了两种不同的观点，怎么办？同桌先讨论一下。

师：现在请双方各派一名代表来阐述一下你的理由。

生1：我方认为陈军没有达标，因为5 小于10。

生2：我方认为陈军达标了。这个5 是记作5，它表示比10 个还多5 个。

生3：我再来补充一下，这个5是+5 的意思，因为正数前面的正号可以省略。

师：现在你们同意他们的观点吗？陈军实际跳了几个？（询问后，条形图演示比达标个数多5 个）

师：张华的成绩记作什么？

生：记作0。因为他的成绩正好达标。（结合学生回答条形图演示记作0）

师：三位同学的成绩分别记作-4，5，0，体育老师为什么这么记？

小结：可以清楚地看出和达标成绩的差距。

在上述这个练习设计中，教师巧妙地将条形统计图作为几何直观的图形，辅助学生进行推理和思维，牢牢扣住标准个数，图中用红色的虚线标注十分醒目，突出了负数概念中关于“标准0”这一本质特征。在此，利用数形结合，帮助学生深化对负数的认识，而且也巧妙地为下节课进一步研究负数做好了准备。

三、依托几何直观组织比较，抽象提炼数量关系模型

数量关系具有高度的抽象性，是具体情境中概括出来的。徐利治先生提出：几何直观是借助见到的或想到的几何图形的形象关系产生对数量关系的直接感知。利用几何图形的直观对问题中的关系和结构进行表述，帮助学生分析问题和解决问题！这是一种非常重要的策略。

常见的数量关系是过去小学数学教学的一个重要内容，修订教材对此项内容引起高度重视。在“常见的数量关系”一课教学时，原本教材只是静态地呈现了两组数量关系的例题，我对此进行了改造，充分挖掘学生购物素材，采撷生活中的数学原型。本课中的单价标签和购物小票等（如下图所示），把数学学习置身于生动有趣的活动中，让学生感受到数学有趣、有用、好学。特别是借助购物小票中几种商品的单价、数量和总价三栏信息，通过引导学生自主交流，发现小票中所蕴含的丰富的信息和数量关系，并通过数形结合，让学生联系线段图初步理解其中隐含的数量关系。在学生掌握了单价、数量和总价之间的乘法数量关系后，我安排了“去哪家买果汁便宜”的购物情境，一方面让学生用乘除法之间的运算经验掌握求单价的数量关系，另一方面巧妙地从单价“元/瓶”的聚焦，让学生萌生“为什么单价的单位要用复合单位”的疑问，在学生提出问题后，教师巧妙借助多媒体动态演示将“元/瓶”中的“/”变化成“÷”的过程，让学生形象理解其中隐藏的数量关系，实现几何直观一箭双雕的作用！

借助几何直观把抽象的数量关系用画图的形式表达出来，是“去情境化”的过程，是一个数学建模的过程。它把情境中的数量关系进行提炼，并且直观表达，然后运用这个数学模型解决类似的问题，形象思维由图形带来的直觉，增进学生对数学的理解，增强其创造能力。化抽象为直观，化内隐为外显，教师依托几何直观的方法从冗长的、大量的问题情境中剥离出共同的数量关系，从而让学生聚焦目光、聚焦问题、聚焦思维，从而数学化地解决问题，提高课堂教学效率。