基于源面板法浸没圆柱倾斜激励水动力学数值模拟

赵乐平， 罗志强， 吕毅斌

(昆明理工大学 理学院 数学系， 云南 昆明 650500)

近水面波体相互作用问题一直是海洋工程领域关注的重点之一，研究水下结构体激励引起的水动力学变化规律具有重要意义。近些年来，有许多学者研究圆柱体激励引起的水动力学变化规律。1961年，YU和URSELL[1]研究了无限水深区域内半浸没圆柱体激励所产生的波。1967年，FRANK[2]利用格林函数研究了圆柱体做摇摆、起伏和滚动3种情况下的阻尼系数和附加质量系数。1971年，DAVIS[3]通过构造适当的广义格林函数，建立了边界积分方程，研究了半浸没球体垂直激励的附加质量。由于浸没体在特定的激励频率内激励时，利用格林函数研究波体相互作用问题会导致最后的数值解会出现较大的误差。1973年，YEUNG[4]提出了Rankine源法，BEDEL和LEE[5]利用源面板法求解了浸没圆柱体激励的附加质量和阻尼系数。2015年左右，FENG等[6-7]通过在漂浮的圆柱体附近放置较密集的源点，在离圆柱体较远的地方放置较为稀疏的源点，研究了半浸没在水中的圆柱体做垂直激励的波体问题。

在时域上，Rankine源面板法相比其他方法，更能有效数值求解波体相互作用问题。本文构造水下圆柱体源分布和自由面源分布，研究水下激励体倾斜激励下圆柱体和自由面的水动力学变化规律。

1 浸没圆柱体激励问题的基本理论

考虑圆柱体在无限水深不可压缩的无旋且无黏性的流体区域中激励，图1给出了无限水深区域内圆柱体激励的物理模型，以水平面中点为坐标原点，x轴水平向右，y轴垂直向上，在静止自由面上建立笛卡尔坐标系。源点q分布在流体区域中，设Sq是以q为圆心、ε为半径的圆的边界。流体区域V由自由面边界SF、圆柱体边界Sb、源点q所围成的区域边界Sε和无穷远处海底边界围成。

图1 浸没圆柱体倾斜激励的物理模型

设ω是倾斜激励频率，a是倾斜激励振幅，圆柱体倾斜激励速度为

V=aωcos(ωt)i+aωcos(ωt)j，

其中i为沿x轴方向的单位向量，j为沿y轴方向的单位向量。

设φ为流体的总速度势，定义速度u和v为

流体区域内的速度势φ满足Laplace方程：

由圆柱体表面的不可渗透边界条件得

(1)

其中nb为圆柱体的外法向量。

由伯努利原理得圆柱体表面压力P的表达式为

设ξ为波高，线性自由面动力学边界条件和运动学自由面边界条件分别为

(2)

(3)

初始条件满足:φ(0)=0，ξ(0)=0。

2 势流方程的边界积分方法

考虑无限水深情况下，在边界Sb和SF上任意一点q分布源流，依据LAMB[8]的理论，流场中任意一点p的总速度势边界积分方程可以表示为

(4)

其中q为源点，p为流域中的任意一点，σb为圆柱体表面分布的源强，σF为自由面分布的源强。

2.1 圆柱体边界积分方程的离散

将圆柱面剖分成Nb等份，自由面剖分成NF等份，如图2所示，流域中的q点移至面板中点，对边界积分方程(5)离散

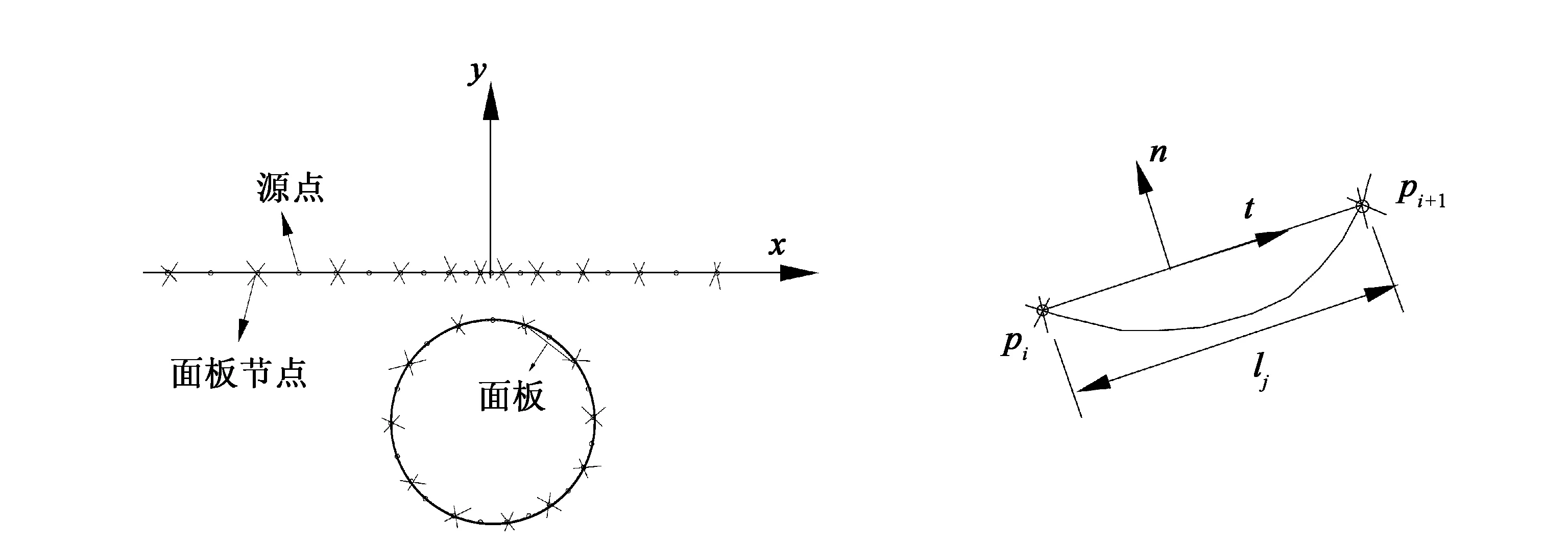
图2 圆柱体表面以及自由面的离散

(5)

其中σb,i∈Sb，σF,j∈SF，i=1，…，Nb，j=1，…，NF。

设圆柱体表面的节点pb,i=(xb,i,yb,i)，pb,i+1=(xb,i+1,yb,i+1)，i=1，…，Nb，则圆柱体表面上的源点、面板长度、面板单位切向量、面板单位法向量分别为

t时刻圆柱体表面第i个面板上的速度势为

(6)

由圆柱体的不可渗透条件式(3)及式(6)得

(7)

其中nb,i为圆柱体每个面板的法向量。

2.2 自由面边界积分方程的离散

设自由面边界的节点pF,j=(xF,j,yF,j)，pF,j+1=(xF,j+1,yF,j+1)，j=1，…，NF。由于在静止自由面上放置源点时，流体区域关于y轴对称，y轴左右侧源点放置方法相同，因此我们只对y轴右侧源点的放置方法进行讨论。取NF=181，在y轴右侧自由面放置90个源点，其中60个点放置在第一区域，30个点放置在第二区域。

第一区域的放置法

第二区域的放置法

其中αj的取值如表1所示。

表1 参数αj的取值

自由面SF上的源点、面板长度、面板单位切向量分别为

由公式(6)得，t时刻自由面第j个面板上的速度势为

(8)

式(8)关于y的偏导为

(9)

为获得任意时刻t自由面上第j个面板的流体速度势φ和波高ξ，在初始条件下，采用二阶亚当斯-贝希霍斯迭代对方程(2)和(3)进行反复迭代。

下面给出自由面速度势φ和波高ξ的迭代算法步骤，其中Δt是时间步长。

(1)给出初始条件φ(0)=0，ξ(0)=0。

(2)当t=1时，采用下面的一阶向前欧拉公式迭代得到下一时刻的速度势φ和波高ξ：

ξ(0+Δt)=vF(pF,j,0)Δt，

φ(0+Δt)=-gξ(0)Δt。

(3)当t>1时，采用下面的二阶亚当斯-贝希霍斯显式公式，对速度势φ和波高ξ进行反复迭代：

2.3 边界积分方程的求解

联立式(7)和(8)得矩阵方程：Aσ=B，其中

系数矩阵A里面的分块矩阵分别为

矩阵方程右端项为

bi=nb,i·V(pb,i,t),i=1,…,Nb，

3 数值算例

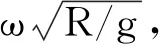
3.1 算法验证

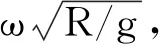
图3 浸没圆柱体垂直激励下自由面波高与文献的比较结果图

3.2 数值结果与讨论

3.2.1 不同激励频率、振幅、水深下圆柱体倾斜激励自由面波高数值模拟

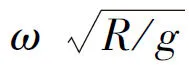
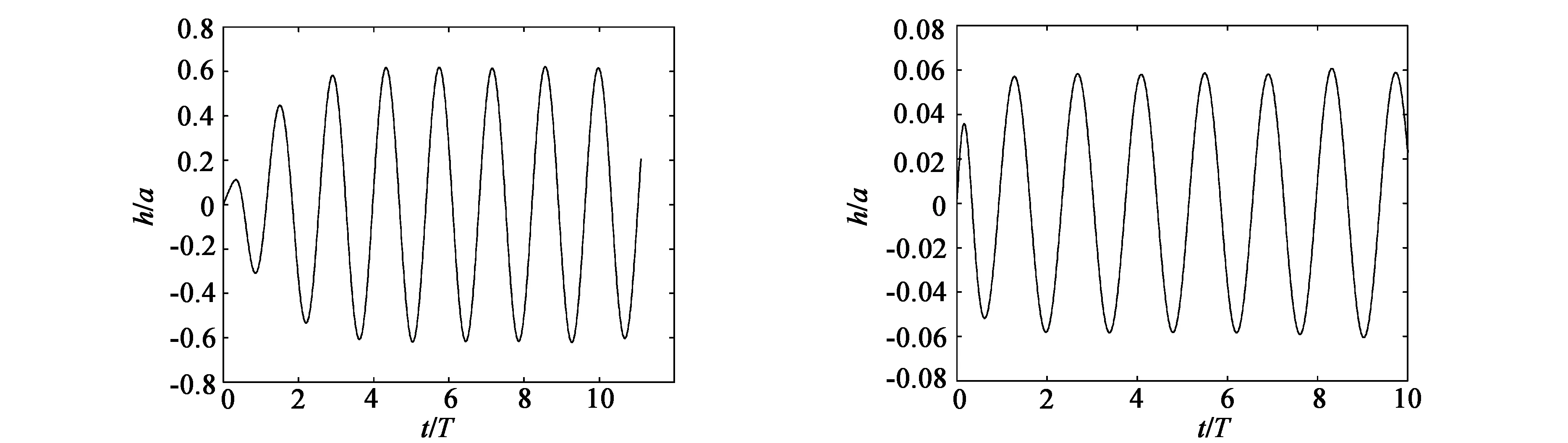
3.2.2 不同水深下浸没圆柱体垂直激励和倾斜激励自由面波数值模拟

本节数值模拟不同浸没深度下圆柱体垂直激励和倾斜激励产生的自由面波高区别，从图5(a)可知当h/R=1.5时，垂直激励和倾斜激励下自由面波的周期时间相同。但倾斜激励下自由面波的波峰和波谷高度略大于垂直激励倾斜激励下自由面波的波峰和波谷高度。由图5(b)可知，当h/R=1.0，垂直激励下自由面波的振幅以及周期时间明显不同于倾斜激励下自由面波的振幅以及周期时间，且倾斜激励下波高随时间变化增长的速度大于垂直激励下波高随时间变化增长的速度。在图5(c)中，取h/R=0.5，与图5(a)和(b)对比可得，浸没深度越小，垂直激励下自由面波的振幅以及周期时间与倾斜激励下自由面波的振幅以及周期时间差别越明显，且倾斜激励下波高随时间变化增长的速度明显大于垂直激励下波高随时间变化速度增长的速度。从图5(a)、(b)、(c)可以看到随着浸没深度的增大，自由面波的振幅变小，垂直激励产生的自由面波和倾斜激励产生的自由面波趋于一致。

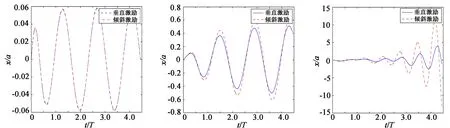
h/R=1.5 h/R=1.0 h/R=0.5

3.2.3 不同水深下圆柱体水平激励和倾斜激励自由面波数值模拟

本节数值模拟不同浸没深度下圆柱体水平激励和倾斜激励产生的自由面波高区别，从图6(a)可知当h/R=1.5时，倾斜激励下自由面波的波峰和波谷高度大于水平激励下自由面波的波峰和波谷高度。在图6(b)中，取h/R=1.0，倾斜激励下自由面波的振幅明显大于水平激励下自由面波的振幅，且倾斜激励下波高随时间变化增长的速度大于水平激励下波高随时间变化增长的速度。在图6(c)中，取h/R=0.5，水平激励与倾斜激励下波高值较为接近，从t/T=2开始，二者的波高差距随时间变化不断增大。从图6(a)、(b)、(c)可以看出随着浸没深度的减小，自由面波的振幅变大，水平激励产生的自由面波趋近于倾斜激励产生的自由面波。

h/R=1.5 h/R=1.0 h/R=0.5

3.2.4 不同激励频率、振幅、水深下圆柱体倾斜激励圆柱体表面压力数值模拟

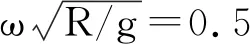
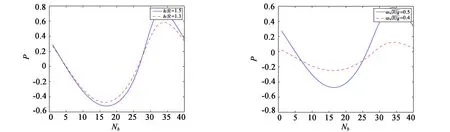
4 小结

本文基于源面板法研究了浸没圆柱体倾斜激励下圆柱体表面压力与波高的水动力学特性，通过数值实验结果可以发现：

(1)当浸没圆柱体倾斜激励时，圆柱体表面压力在不同时刻取值不同，随着激励频率、振幅以及浸没深度的增大而增大。自由面波高随时间先增长后趋于稳定，呈线性变化，激励频率和振幅越大浸没深度越小，自由面波的振动幅度越大，波高随时间变化呈增长状态的时长越短。

(2)圆柱体垂直激励下，浸没深度越大，自由面波高随时间变化增长越缓慢，越趋近于浸没圆柱体倾斜激励下自由面波的变化规律。

(3)圆柱体水平激励下，浸没深度越小，自由面波高随时间变化呈增长的状态越明显，越趋近于浸没圆柱体倾斜激励下自由面波的变化规律。