需求冲击下的产能过剩:一个分析框架
2020-08-20皮建才张鹏清
皮建才 张鹏清
(南京大学 经济学院,江苏 南京 210093)
一、引言
各种不同类型的外部冲击会引起需求不确定。需求冲击引致的需求不确定是我们在进行经济分析时必须考虑的一个重要因素,特别是在产能投资领域。需求冲击引致的需求不确定对产能投资和产能过剩的影响一直都是学术界关注的热点、重点和难点问题。产能过剩问题不能只考虑供给侧而不考虑需求侧,也不能只考虑需求侧而不考虑供给侧,必须把供给侧和需求侧结合在一起进行考虑。而一旦将供给侧和需求侧结合在一起,我们就必须考虑需求不确定。
寇宗来认为,当存在外包机会时,为了降低需求不确定引致的风险损失,厂商将会策略性地降低产能投资[1]。胡川认为,由于需求不确定,企业实际的产能可能大于古诺均衡条件下所需要的产能,原因在于企业对需求的预测并不是那么精准,只是一种近似[2]。Lu和Poddar认为,在混合双寡头市场中,需求不确定会使得国有企业和民营企业都出现产能过剩或者产能不足的对称结果,或者出现国有企业产能不足但是民营企业产能过剩的不对称结果[3]。徐朝阳和周念利认为,当行业的发展前景比较确定但是需求不确定比较大时,高效率的企业为了降低需求不确定引致的风险损失,会在产能投资上比较谨慎,这就给低效率的企业留下了产能投资的空间,从而导致产能利用率比较低[4]。皮建才和卜京认为,需求不确定的增加会抑制企业的产能投资,减少企业的体制性产能过剩[5]。但是,一方面,现有的文献考虑的是总体的需求冲击和需求不确定性,并没有考虑需求不确定在博弈中哪一阶段实现,也没有考虑需求不确定冲击是政府决策还是厂商决策,抑或是同时冲击这两个决策;另一方面,现有的绝大多数文献往往忽视了体制性产能过剩,虽然皮建才和卜京考虑到了体制性产能过剩[5],但在作用机制和研究结论上与本文有根本性的不同。本文试图从以上两个方面填补现有文献的不足之处。
本文同时考虑了产能过剩和体制性产能过剩。所谓的体制性产能过剩是指由于政府补贴而引起的产能过剩[6][7][8]。从数理角度来看,体制性产能过剩是指存在政府补贴时的产能过剩减掉不存在政府补贴时的产能过剩。耿强等以及王自锋和白玥明在进行理论和经验分析时把产能过剩分成了竞争性产能过剩和体制性产能过剩,这种分类可以很好地跟本文的博弈模型对应[9][10]。另外,与本文比较相关的产能过剩文献还包括Vany和Frey以及Pindyck的研究,他们认为产能过剩是应对市场需求变化和潜在竞争对手的威胁,这实际上意味着市场竞争本身就会引起产能过剩[11][12]。
我们的研究发现:第一,无论是当只有政府面临需求不确定时,还是当厂商和政府均面临需求不确定时,抑或是在政府进行补贴决策和厂商进行产能决策面临需求不确定时,政府补贴都会引致体制性产能过剩,而且政府补贴率越高,体制性产能过剩程度越高。第二,当只有政府面临需求不确定时或者当厂商和政府均面临需求不确定时,市场竞争会引致产能过剩。第三,在政府进行补贴决策和厂商进行产能决策面临需求不确定时,只有当已实现的市场规模较小时,才会出现产能过剩;而当已实现的市场规模较大时,则会出现产能不足。
二、模型构建
假设经济体中存在两家厂商,分别是厂商1和厂商2。此外,还有一个政府部门。企业决定其产能投资水平和产量水平,追求利润最大化。政府制定对企业的补贴率,以实现社会福利和总产出的加权最大化。根据Lu和Poddar等学者的研究[3][13],设定厂商j的成本函数如下:
Cj(xj,qj)=mqj+(xj-qj)2
(1)
式(1)中,j∈{1,2},qj是厂商j的产量,xj是厂商j的产能,m衡量厂商j的生产效率。不失一般性地,本文假设厂商1和厂商2的生产效率是一样的,以便把关注点放在市场需求的不确定上,而非企业的异质性上。从成本函数中我们可以发现,厂商产能过剩(即xj>qj)和产能不足(即xj p(q1,q2;ai)=ai-(q1+q2) (2) 厂商j的利润函数可以表示为如下的形式: πj(xj,qj;ai)=pqj-mqj-(xj-qj)2+sqj (3) 式(3)中,j∈{1,2},s表示政府制定的补贴率,从而sqj就表示厂商j收到的政府补贴。厂商的目标是最大化利润,但在进行产量决策之前,必须先进行产能决策。这样的决策顺序符合现实,厂商必须先投资产能,然后才能进行生产。政府部门制定补贴率s以最大化社会福利和总产出的加权,其目标函数如下: W(s;ai)=CS+π1+π2-s(q1+q2)+λy (4) 博弈的时序如下:第一阶段,政府部门制定最优的补贴率,以最大化社会福利和总产出的加权;第二阶段,厂商1和厂商2同时进行产能决策,以最大化各自的利润;第三阶段,厂商1和厂商2同时进行产量决策,以最大化各自的利润。政府和厂商都是风险中性的。 本文的创新之处是,考虑了需求不确定在博弈中的实现,特别是考虑了需求不确定冲击的是政府决策还是厂商决策,抑或是同时冲击这两个决策。具体而言,本文考虑了三种不同的情况:一是衡量市场规模的随机变量ai在第一阶段和第二阶段博弈之间实现,即当政府部门决策时,ai是未知的,当厂商决策时,ai是已知的;二是随机变量ai在第二阶段和第三阶段博弈之间实现,即只有到了厂商进行产量决策时,ai才是已知的;三是随机变量ai在博弈结束后才实现,即对于政府和厂商而言,ai都是未知的。本质上,我们可以引入“自然”作为博弈方参与到博弈当中,由其决定随机变量ai的实现。需求冲击的现实含义为:在现实经济中,从政府出台补贴政策,到企业投资设备厂房形成产能,到企业生产销售产品,再到最终消费,都存在一定的时滞,中间如果受到需求不确定性的冲击,那么政府和企业的决策很可能发生变化。衡量市场规模的随机变量ai还可能在第一阶段之前实现,但这种情况相当于经济体中不存在需求不确定,因为在这种情况下,需求不确定并不影响博弈方的决策。 下文分三种情况进行分析:第一种情况是只有政府面临需求不确定;第二种情况是政府进行补贴决策和厂商进行产能决策时面临需求不确定;第三种情况是厂商和政府均面临需求不确定。我们之所以区分三种情况,是因为在三阶段博弈中,随机变量可能在第一阶段和第二阶段博弈之间实现,也可能在第二阶段和第三阶段博弈之间实现,还可能在博弈结束后方实现。 我们先考虑第一种情况,即衡量市场规模的随机变量ai在第一阶段和第二阶段博弈之间实现,所以当政府部门决策时,ai是未知的,当厂商决策时,ai是已知的。 因为在厂商进行决策时,ai是已知的,所以我们运用逆推归纳法求解第三阶段和第二阶段时,厂商最大化的是实际利润,而非期望利润。 在第三阶段,厂商1和厂商2选择产量以最大化各自的利润。对于每一个已实现的市场规模a,联立求解厂商1和厂商2的一阶条件可以得到: (5) (6) 式(5)和式(6)中,a表示随机变量ai的实现值。 在第二阶段,厂商1和厂商2选择产能以最大化各自的利润。将式(5)和式(6)代入厂商1和厂商2的利润函数,联立求解厂商1和厂商2的一阶条件可以得到: (7) 将式(7)代回式(5)和式(6)可以得到厂商1和厂商2的产量: (8) 定义厂商j的过剩产能为ej=xj-qj,其中j∈{1,2}。 我们很容易得到命题1。 命题1:当只有政府面临需求冲击引致的需求不确定时,对于任意已实现的市场规模,市场竞争会导致厂商出现产能过剩,政府补贴则会引起体制性产能过剩,且政府补贴的力度越大,体制性产能过剩越严重。 命题1背后的经济学含义如下:给定任意已实现的市场规模,在市场竞争中,厂商在第二阶段选择投资过高的产能水平,实质上是一种阻吓策略,为的是降低第三阶段增加生产以抢占市场的成本。命题1说明市场竞争本身也会导致过剩产能。当政府对厂商提供补贴时,厂商在第三阶段面临对手扩大生产的潜在威胁更大了,为应对潜在的威胁,厂商会在第二阶段投资更高的产能,从而引起体制性产能过剩。 对于第一阶段的政府决策,因为此时ai未知,政府最大化的是期望收益,其表达式如下: (9) 对于每一个可能实现的市场规模a,政府知道厂商将按式(7)和式(8)进行产能决策和产量决策。所以,将式(7)和式(8)代入政府的期望收益(即式(9)),求解政府部门的一阶条件可以得到: (10) 式(10)中,上标*表示第一种情况的均衡解,下同。 将式(10)代入式(7)和式(8)可以求得厂商1和厂商2的均衡产能和均衡产量: (11) (12) 由此,我们可以得到均衡时的过剩产能: (13) 我们可以得到命题2。 命题2:当只有政府面临需求冲击引致的需求不确定时,若期望的市场规模比较小,政府越重视GDP,则产能过剩和体制性产能过剩越严重,相应的补贴力度也越大。相反,若期望的市场规模比较大,政府重视GDP能在一定程度上缓解产能过剩和体制性产能过剩,相应的补贴力度也较小。 命题2的含义符合经济学直觉。如果期望的市场规模比较小,那么取得一个高的GDP就会比较困难。此时,政府越重视GDP,其提供的补贴力度相对期望的市场规模而言就越大,反而越加重经济体的产能过剩和体制性产能过剩,因为较小的市场规模压缩了厂商的生产空间。反之,如果期望的市场规模比较大,那么取得高的GDP相对容易。此时,政府对GDP的重视反而会激励厂商充分利用已投资的产能增加产量,从而减少产能过剩和体制性产能过剩。 我们现在考虑第二种情况,即衡量市场规模的随机变量ai在第二阶段和第三阶段博弈之间实现,所以只有到了厂商进行产量决策时,ai才是已知的。 因为在厂商进行产量决策时,ai是已知的,所以我们运用逆推归纳法求解第三阶段时,会得到第一种情况对应的结果,即式(5)和式(6)。 当厂商在第二阶段决定产能时,因为ai是未知的,所以厂商选择产能以最大化期望利润,其表达式如下: (14) 对于每一个可能实现的市场规模a,厂商知道他们将在第三阶段按照式(5)式和式(6)决定产量水平,所以把式(5)和式(6)代入式(14),联立求解厂商1和厂商2的一阶条件可以得到: (15) 将式(15)代回式(5)和式(6)可以得到厂商1和厂商2的产量: (16) 由此,我们可以得到命题3。 命题3:在政府进行补贴决策和厂商进行产能决策面临需求冲击引致的需求不确定时,对于任意已实现的市场规模,政府补贴会引起体制性产能过剩,且政府补贴的力度越大,体制性产能过剩越严重。但是,只有当已实现的市场规模较小时,才存在产能过剩的情况;而当已实现的市场规模较大时,则会出现产能不足的情况。 命题3说明在政府进行补贴决策和厂商进行产能决策面临需求不确定时,厂商可能会出现产能不足的情况。一方面,政府补贴会刺激厂商投资产能,引起体制性产能过剩,这种情形已在命题1后进行了阐释。另一方面,当厂商进行产量决策时,如果已实现的市场规模较小,那么厂商在不清楚市场规模时投资的产能就会超过实际的需要,从而引起产能过剩。反之,如果已实现的市场规模较大,那么厂商之前投资的产能就会不足,厂商情愿多生产以获取更大的利润。但是,不管已实现的市场规模如何,政府补贴对产能过剩的贡献总是正的。 对于第一阶段的政府决策,因为此时ai未知,所以政府最大化的是期望收益。将式(15)和式(16)代入政府的期望收益(即式(9)),求解政府部门的一阶条件可以得到: (17) 式(17)中,上标#表示第二种情况的均衡解,下同。 将式(17)代入式(15)和式(16)可以求得厂商1和厂商2的均衡产能和均衡产量: (18) (19) 从而,我们可以求得厂商1和厂商2的过剩产能: (20) 由此,我们可以得到命题4。 命题4:在政府进行补贴决策和厂商进行产能决策面临需求冲击引致的需求不确定时,若期望的市场规模比较小,政府越重视GDP,则产能过剩和体制性产能过剩越严重,相应的补贴力度也越大。相反,若期望的市场规模比较大,则政府重视GDP能在一定程度上缓解产能过剩和体制性产能过剩,相应的补贴力度也较小。 命题4的证明与命题2的证明类似,此处省略。 命题4可以按照命题2背后的经济学直觉进行解释和理解。 最后我们分析第三种情况,即衡量市场规模的随机变量ai在博弈结束后方才实现,所以对于政府和厂商而言,ai都是未知的。 我们还是用逆推归纳法分析。首先看第三阶段厂商进行产量决策,此时由于ai未知,厂商最大化的是期望利润(即式(14))。联立求解厂商1和厂商2的一阶条件可以得到: (21) (22) 从式(21)和式(22)中可以发现,当存在需求不确定时,厂商根据期望的市场规模进行产量决策。 考虑第二阶段厂商进行产能决策。将式(21)和式(22)代入企业的期望利润,联立求解厂商1和厂商2的一阶条件可以得到: (23) 我们可以发现,式(23)和式(15)是一样的,说明当厂商在产能决策阶段面临需求不确定时,反应函数与厂商是否在产量决策时面临需求不确定无关。 将式(23)代入式(21)和式(22)可以得到厂商1和厂商2的产量: (24) 从式(23)和式(24)可以发现,厂商根据期望的市场规模决定产能和产量。 由此,我们可得到命题5。 命题5:当厂商和政府均面临需求冲击引致的需求不确定时,市场竞争会导致厂商出现产能过剩,政府补贴则会引起体制性产能过剩,且政府补贴的力度越大,体制性产能过剩越严重。 命题5的证明与命题1的证明类似,在此不再重复。 命题5的经济学含义与命题1的经济学含义是基本一致的。厂商虽然面临不确定的需求,但可以按照期望的市场规模进行产能决策和产量决策。从而,厂商的策略就类似于在产能决策和产量决策时市场规模已实现的情况(即第一种情况)。 再看第一阶段政府的决策,此时由于ai未知,政府最大化的是期望收益(即式(9))。将式(23)和式(24)代入政府的目标函数,求解政府部门的一阶条件可以得到: (25) 式(25)中,上标Λ表示第三种情况的均衡解,下同。 将式(25)代入式(23)和式(24)可以求得厂商1和厂商2的均衡产能和均衡产量: (26) (27) 我们可以发现,均衡的产能和式(18)是一样的。 我们可以求得厂商1和厂商2的过剩产能: (28) 类似于命题2和命题4,我们可以得到命题6。 命题6:当厂商和政府均面临需求冲击引致的需求不确定时,若期望的市场规模比较小,政府越重视GDP,则产能过剩和体制性产能过剩越严重,相应的补贴力度也越大。相反,若期望的市场规模比较大,政府重视GDP能在一定程度上缓解产能过剩和体制性产能过剩,相应的补贴力度也较小。 命题6的证明与命题2的证明类似,此处省略。 命题6的经济学含义与命题2的经济学含义是基本一致的,只是厂商按照期望市场规模进行决策。 通过比较第三部分所讨论的三种情况,我们可以归纳出如下四个命题。 命题7:当存在需求冲击引致的需求不确定时,无论不确定的需求在哪一阶段实现,政府的最优补贴力度都是相同的。 命题7说明,当存在需求不确定时,政府会按照期望的市场规模制定其补贴力度,引导厂商进行产能决策和产量决策。对于政府部门而言,需求不确定在哪一阶段实现无关紧要,关键是政府进行补贴决策时不知道具体的需求是什么。政府通过按照期望的市场规模制定补贴力度最大化其目标函数。 命题8:当存在需求冲击引致的需求不确定时,只有当厂商在产能决策时面临需求不确定,而在产量决策时需求不确定已实现的时候,才有可能出现产能不足的情况。但是,无论不确定的需求在哪一阶段实现,都会出现体制性产能过剩。 证明:综合命题1、命题3和命题5可以得到命题8。 命题8说明当厂商在产能决策时面临需求不确定,而在产量决策时需求不确定已实现的时候,需求不确定可以视作厂商限制对方把产能作为产量威胁的一种装置。因为厂商在产能决策时,需求是未知的,未知的需求会限制两个厂商的产能投入。如果在产量决策时,实现的需求比较高,那么厂商就有足够的利润动机扩大生产,从而导致产能的不足。但是,值得注意的是,政府补贴仍然会造成体制性产能过剩,这与确定的需求在哪一阶段实现无关。这是因为政府补贴并未改变厂商把已投资的产能视为沉没成本的事实,所以政府补贴虽然同时放大了产量和产能,但对产能的放大程度更大,从而引起了体制性产能过剩。 命题9:当存在需求冲击引致的需求不确定时,无论不确定的需求在哪一阶段实现,若期望的市场规模比较小,政府越重视GDP,则产能过剩和体制性产能过剩越严重,相应的补贴力度也越大。相反,若期望的市场规模比较大,则政府重视GDP能在一定程度上缓解产能过剩和体制性产能过剩,相应的补贴力度也较小。 证明:综合命题2、命题4和命题6可以得到命题9。 命题9揭示了需求不确定背景下政府关注GDP增长与产能过剩和体制性产能过剩的关系。如果经济下行、外部需求下降等因素导致期望的市场规模比较小,那么政府对GDP增长的重视反而会加重产能过剩和体制性产能过剩。这背后的经济学逻辑如下:根据命题7,当存在需求不确定时,无论不确定的需求在哪一阶段实现,政府都会制定相同的补贴力度。如果期望的市场规模比较小,政府需要加大补贴力度来刺激厂商扩大生产,但因市场规模较小,厂商并不会利用这部分产能,从而加剧产能过剩和体制性产能过剩。如果期望的市场规模比较大,厂商可以比较充分地利用已投资的产能,此时政府对GDP的关注能在一定程度上缓解产能过剩和体制性产能过剩。 命题10:当只有政府面临需求冲击引致的需求不确定时,实现的市场规模越大,厂商的产能水平和产量水平就越高,产能过剩也越严重。但是,在政府进行补贴决策和厂商进行产能决策面临需求不确定时,实现的市场规模越大,虽然产量水平也越高,但产能过剩的程度会越小,而产能水平则不受所实现的市场规模的影响。 命题10是命题8的延伸,说明厂商在进行产能决策时需求是否实现会对结果有重大影响。当只有政府面临需求不确定时,厂商进行产能决策时需求函数是已知的。此时,如果实现的市场规模比较大,那么厂商面临较大的市场规模时会自然而然地提高产能和产量水平,造成的产能过剩也比较严重。如果厂商进行产能决策时需求函数是未知的,那么厂商会按照期望的市场规模进行产能投资。此时,如果在产量决策时实现的市场规模比较大,厂商就会增加产量。因为按照期望的市场规模投资的产能水平与实现的市场规模无关,所以此时厂商增加产量会降低产能过剩。 本文为需求冲击引致的需求不确定下的产能过剩和体制性产能过剩建立了一个新的分析框架,该分析框架既考虑了需求冲击引致的需求不确定在博弈中哪一阶段的实现,也考虑了需求冲击引致的需求不确定影响的是政府决策还是厂商决策,抑或是同时影响这两者的决策。我们考虑的这两个因素正是现有文献所忽视的,所以纳入这两个因素进行分析构成了本文区别于现有文献的学术贡献。 我们需要把竞争引起的产能过剩和补贴引起的体制性产能过剩区分开来,在需求冲击的框架下分类治理产能过剩和体制性产能过剩。根据命题2、命题4和命题6,政府重视GDP不一定会加重产能过剩和体制性产能过剩,这要看期望的市场规模比较大还是比较小。当期望的市场规模比较大时,政府重视GDP反而能在一定程度上缓解产能过剩和体制性产能过剩。这就表明,我们治理产能过剩和体制性产能过剩不能“一刀切”,治理政策需要考虑需求不确定的作用,识别不同行业面临的不同需求不确定,识别不同行业的不同期望市场规模。一旦把需求不确定纳入政策制定的考虑范畴,一些传统的治理产能过剩和体制性产能过剩的措施则需要进行反思和修正,甚至包括一些识别僵尸企业的政策也需要进行反思和修正。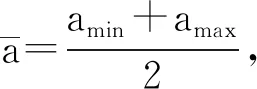
三、博弈均衡结果
(一)只有政府面临需求不确定

(二)政府进行补贴决策和厂商进行产能决策时面临需求不确定
(三)厂商和政府均面临需求不确定
四、比较分析
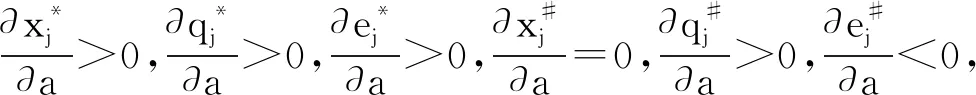
五、结语
