Frobenius扩张下的丁投射(内射)模
2020-08-19赵自红
苗 壮,赵自红
(兰州理工大学理学院,甘肃 兰州 730050)
1 预备知识
研究中,R表示有单位元的结合环,Rop是R的反环,左R-模M通常记为RM,右R-模M通常记为MR,模M的Ding投射维数记为DpdR(M)。记环扩张l:RA为R⊂A。自然双模RAR由rar=l(r)·a·l(r′)定义给出。类似地,我们考虑RA,RAA等。对于环扩张R⊂A,存在A-模范畴到R-模范畴的限制函子Res:Mod(A)→Mod(R)。另一方面,存在R-模范畴到A-模范畴的函子T=A⊗R-:Mod(R)→Mod(A)与H=HomR(A,-):Mod(R)→Mod(A),其中(T,Res)与(Res,H)是伴随对。Ren[1]介绍了在环的Frobenius扩张下Gorenstein投射(内射)模与Gorenstein投射(内射)维数的相关性质,证明了左A-模M是Gorenstein投射(内射)的当且仅当作为左R-模时,M是Gorenstein投射(内射)的。Yang等[2]研究了丁投射(丁内射)模。受到文献[1-10]的启发,研究探讨了Frobenius扩张下丁投射(内射)模相关性质,证明了在任意结合环R上,若环扩张R⊂A是Frobenius扩张,对于Frobenius扩张下的丁投射(内射)模,任意的左A-模M是丁投射(内射)的当且仅当作为左R-模时M是丁投射(内射)的。
2 主要结果
定义1称环扩张R⊂A是Frobenius扩张,如果满足下列等价条件中的任意一条:
(1) 函子T=A⊗R-与H=HomR(A,-)是自然等价的;
(2)RA是有限生成投射的且AAR≅(RAA)*≅HomR(AAR,R);
(3)AR是有限生成投射的且RAA≅(AAR)*≅HomRop(RAA,R);

定义2称左R-模M是丁投射模,若存在R-模正合列P:=…→P1→P0→P0→P1→…,其中Pi、Pi均是投射模,i是非负整数,并且对于任意平坦R-模F,HomR(-,F)作用在正合列P上保持正合,使得M=ker(P0→P1)。在此条件下,我们称P是M的强完全投射分解。

定义4称左R-模M是丁内射模,若存在R-模正合列E:=…→E1→E0→E0→E1→…,其中Ei、Ei均是内射模,i是非负整数,并且对于任意FP-内射R-模L,HomR(L,-)作用在正合列E上保持正合,使得M=ker(E0→E1)。在此条件下,我们称E是M的强完全内射分解。
定义5设M是任意的左R-模。模M的丁投射维数定义为DpdR(M)=inf{n|存在正合列0→Dn→Dn-1→…→D1→D0→M→0,其中Di是丁投射模,i、n均是非负整数且i≤n}。
定义6设M是任意左R-模。模M的丁内射维数定义为DidR(M)=inf{n|存在正合列0→M→E0→E1→…→En-1→En→0,其中Ei是丁内射模,i、n均是非负整数且i≤n}。
定理7对于任意的结合环R,左R-模M是平坦模当且仅当M是有限生成自由左R-模的正向极限[3]。
定理8丁投射模类是投射可解的[2]。
推论9丁投射模保持直和与直和项[4]。
引理10设M是具有有限丁投射维数的左R-模,其中n是整数,则下列条件等价[5]:
(1) DpdR(M)≤n;
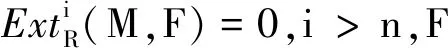
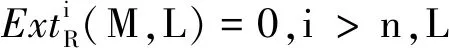
(4) 对于任意的正合列0→Kn→Gn-1→…→G0→M→0,若Gn-1,…,G0是丁投射模,则Kn也是丁投射模。
命题11模M是丁投射的当且仅当存在正合列0→M→P→N→0,其中P是投射模,N是丁投射模[6]。
定理12设R⊂A是环的Frobenius扩张,M是任意左A-模,则下列条件等价:
(1)AM是丁投射模;
(2) 作为左R-模,RM是丁投射模;
(3)A⊗RM与HomR(A,M)是丁投射左A-模。
证明(1)⟹(2) 因为AM是丁投射左A-模,所以存在强完全投射分解P:=…→P1→P0→P0→P1→…,其中Pi、Pi是投射模,i是非负整数,使得M=Ker(P0→P0)。通过限制P我们得到R-模正合列。因为对于任意平坦左R-模Q,HomR(A,Q)≅A⊗RQ是平坦左A-模,所以有HomR(P,Q)≅HomR(A⊗AP,Q)≅HomA(A,Q),因此HomR(P,Q)是正合的。故R-模M是丁投射的。
(2)⟹(3) 设P:=…→P1→P0→P0→…是R-模强完全投射分解,其中M=Ker(P0→P0)。容易验证A⊗RP是A-模正合列,且A⊗RM≅Ker(A⊗RP0→A⊗RP0)。因此A⊗RM与HomR(A,M)是丁投射左A-模。
(3)⟹(2) 对于任意的左A-模M限制在R-模上,RM是R-模A⊗RM的直和项。若A⊗RM是丁投射左A-模,则由(1)⟹(2)知A⊗RM是丁投射左R-模。因此由推论9知RM是丁投射左R-模。
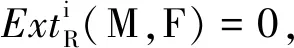





图1 交换图1 Fig.1 Commutative diagram 1



图2 交换图2 Fig.2 Commutative diagram 2

定理13设R⊂A是环的Frobenius扩张,M是任意的左A-模,则下列条件等价:
(1)AM是丁内射模;
(2) 作为左R-模,RM是丁内射模;
(3)A⊗RM与HomR(A,M)是丁内射左A-模。
证明类似于定理12的证明。
引理14设M是任意的左A-模。考虑这样2个复形正合列:
0→Hn→Dn-1→…→D0→M→0,
0→H′n→D′n-1→…→D′0→M→0,
其中Dn-1,…,D0与D′n-1,…,D′0是丁投射模,则Hn是丁投射模当且仅当H′n是丁投射模。
命题15设0→K→G→M→0是R-模正合列,其中G是丁投射模,且DpdR(M)=n,n是整数。若M是丁投射的,则K也是。否则DpdR(K)=DpdR(M)-1。


证明由推论9知对于″≤″是显然的。
反过来,设M′是M的直和项,只需证明DpdR(M′)≤DpdR(M)。设DpdR(M)=n<∞,n是非负整数。对n进行归纳,当n=0时,显然成立。n>0时,不妨设M=M′⊕M″。假设当n-1时成立,选取正合列
0→K′→G′→M′→0, 0→K″→G″→M″→0,
(1)
其中:G′,G″是投射的,则存在如下行可裂的图3。
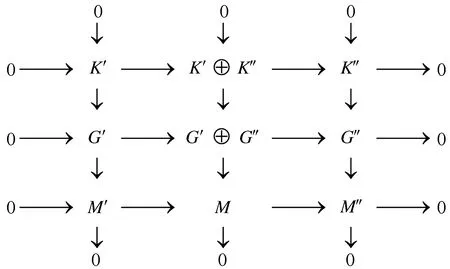
图3 交换图3 Fig.3 Commutative diagram 3
对中间列应用命题15,有DpdR(K′⊕K″)=DpdR(M)-1=n-1。因此,由归纳假设得GpdR(K′)≤n-1。故由正合列(1)知
DpdR(M′)≤n。
命题17设R⊂A是环的Frobenius扩张。对于任意左R-模M,若DpdA(M)<∞,则DpdA(M)=DpdR(M)。
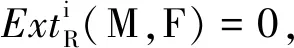
命题18设R⊂A是环的Frobenius扩张。对于任意左A-模M,若DidA(M)<∞,则
DidA(M)=DidR(M)。
证明类似于命题17的证明。
命题19设R⊂A是环的Frobenius扩张,M是任意的R-模,则
DpdA(M)=DpdA(A⊗RM)=DpdR(A⊗RM)。
证明由定理12知
DpdR(A⊗RM)≤DpdA(A⊗RM)。
对于任意的丁投射R-模G,由定理12知A⊗RG是丁投射A-模,故DpdA(A⊗RM)≤DpdR(M)。在定义φ(a)(c)=ac下,限制在R-模上,M是A⊗RM的直和项,由命题15知
DpdR(M)≤DpdR(A⊗RM)。
命题20设R⊂A是环的Frobenius扩张且M是任意的R-模,则
DidA(M)=DidA(A⊗RM)=DidR(A⊗RM)。
证明类似于命题19的证明。
