基于BAS-BP模型的谐波检测
2020-08-19孙飞跃
孙飞跃,吴 雷
(江南大学 物联网工程学院,江苏 无锡 214000)
0 引 言
电力电子技术的不断发展,使得电能得到了更加充分的利用。与此同时,各种非线性负载的存在,也向电网中注入了大量的谐波,严重威胁电力系统的安全运行[1],谐波治理已经成为当前电力系统中的一个重要研究课题。有源电力滤波器(Active Power Filter,APF)可以有效抑制电网谐波,实际应用过程中不需要各次谐波的具体数值,只需要知道总的谐波数据,从而产生相应的波进行抵消。当前常用的谐波检测方法,按照检测原理可归纳为:(1)基于傅里叶变换理论的谐波检测方法;(2)基于瞬时无功功率理论的谐波检测方法;(3)基于神经网络的谐波检测方法;(4)基于小波变换理论的谐波检测方法[2]。本文采用BAS-BP模型检测电力系统中的谐波,并通过仿真说明本方案的可行性和优越性。
1 谐波检测方法研究
1.1 瞬时无功功率理论
瞬时无功功率理论由赤木泰文于1983年提出,由于是建立在瞬时值基础上,瞬时无功功率理论具有较高实时性,能够满足有源电力滤波器对于实时性的需求,因而成为当前应用最为广泛的谐波检测算法。基于瞬时无功功率理论的谐波检测算法可分为p-q法和ip-iq法,其中ip-iq法的谐波检测仿真系统如图1所示。由于ip-iq法在检测过程中不需要用到电压的瞬时值,检测结果不会受到电压畸变或电网电压不对称影响,应用更为广泛。
基于瞬时无功功率理论的谐波检测算法涉及到的坐标变换复杂,低通滤波器的引入使得系统的谐波检测存在延时[3]。对于非稳态电流的谐波检测,该检测方法有很大局限性。
1.2 BP神经网络
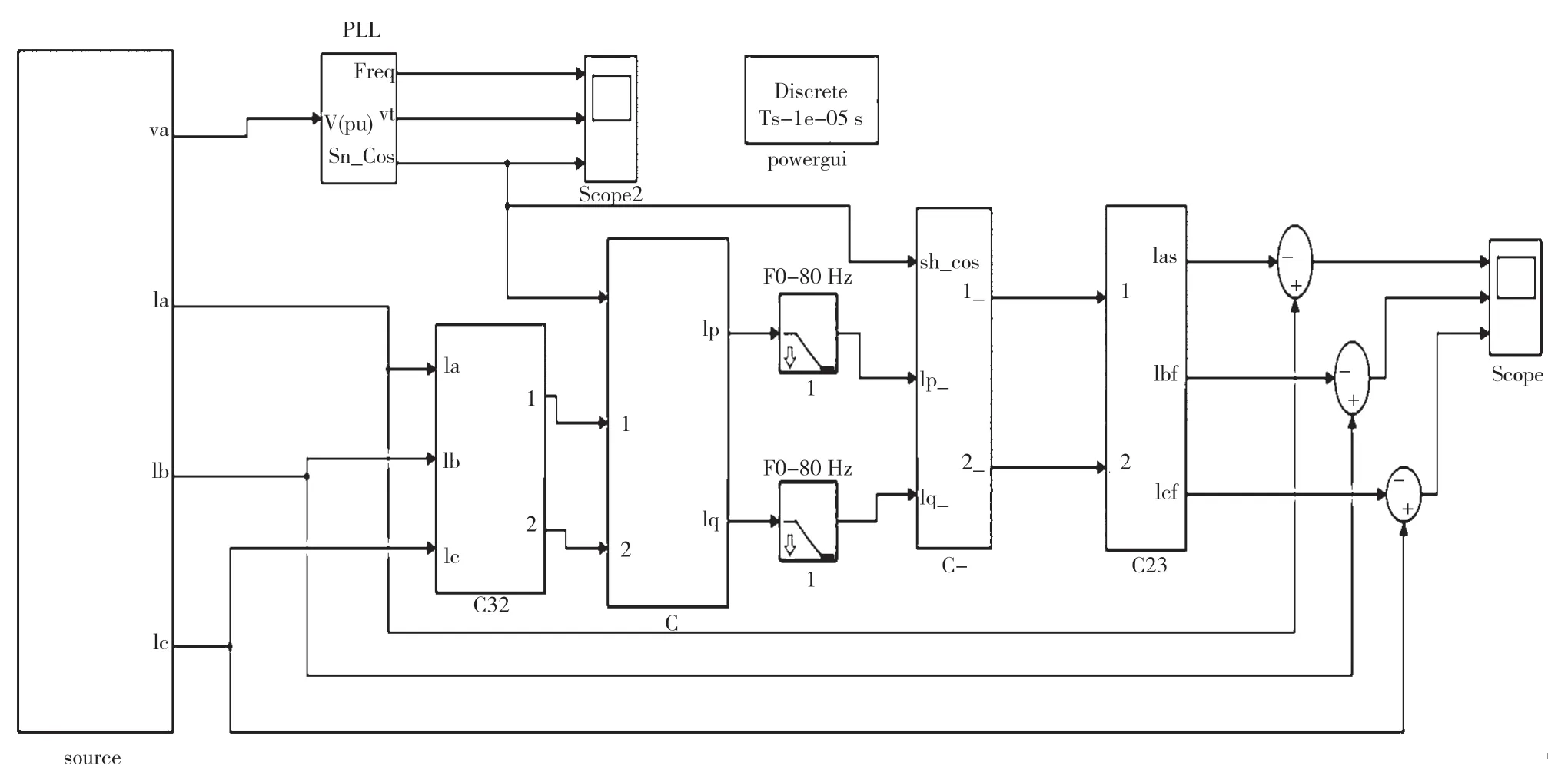
图1 基于ip-iq理论的谐波检测模型
随着神经网络研究的不断深入,基于神经网络的谐波检测算法凭借着强大的自适应能力,在谐波检测领域得到了快速发展。其中,BP(Back Propagation)神经网络应用最为广泛。BP神经网络又名误差反向传播神经网络,属于有导师学习算法,网络结构简单,计算量小,准确度高[4]。BP神经网络可以看成是输入和输出之间的一种非线性映射,可分为输入层、隐含层和输出层。信号从输入层经隐含层逐层计算,最终由输出层输出,比较此时模型输出结果与给定训练样本结果的误差;若不满足网络设定的精度要求,则进行误差的反向传播,将误差通过隐含层向输入层传导,通过相应算法调整神经网络的各层权阈值。经过多次循环,直到训练的网络能够满足预设的精度要求或达到预设的最大训练次数[5]。
BP神经网络的反向传播过程通常采用的是基于梯度下降的算法。实际操作过程中,BP神经网络训练容易陷入局部最优[6],表现出来的特征就是BP神经网络的权阈值收敛达到稳定,但是网络误差不是最小[7]。对于BP神经网络陷入局部最优问题,常见的处理方式是带入训练样本数据进行重新训练,但是这样会浪费很多时间,并且不能保证下一次训练能跳出局部最优,神经网络的训练效率低且最终得到的模型精度不高。已有研究说明,采用相关智能算法对BP神经网络的初始权阈值进行优化,然后再对网络进行二次训练,能在很大程度上提升网络性能,极大避免随机初始化权阈值带来的局部最优问题。例如,可以采用遗传算法或粒子群算法寻找合适的BP神经网络初始权阈值[8-9]。但是这两种算法都是基于群体算法,算法本身需要设置参数较多,且不同的参数设置对最终结果影响较大。同时,实际使用过程中,参数需要根据不同情况进行多次调试,算法使用难度大。
2 BAS-BP神经网络模型
2.1 BAS原理
天牛须搜索[10](Beetle Antennae Search,BAS)算法是2017年提出的一种函数寻优算法,算法的灵感来自于天牛觅食:天牛头部有两只长的触角,如果左边触角感知到的食物气味信息更强,天牛下一步就朝向左边飞,反之朝向右飞,直至最终寻找到目标食物。BAS算法优点在于:BAS可以在不知道函数具体形式的情况下实现自动寻优,并且其个体仅为一个,相比较于遗传算法和粒子群算法,计算量明显缩小,寻优速度更快。
2.2 BAS-BP建模
BAS-BP模型创建步骤如下。
第一,假设天牛在任意时刻的头部朝向随机,确定BP神经网络的空间维度k。k的大小等于BP神经网络中权阈值个数的和。

第二,设置天牛行进步长δ。天牛的行进采用线性缩减策略,保证天牛搜索精细化,即:
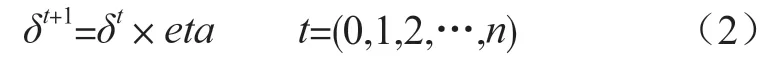
其中,本文取eta=0.85。
第三,自定义适应度。本文以测试数据的均方误差MSE作为适应度,具体为:

其中:N为模型训练集样本总个数;tsim(i)为第i个样本的模型输出值;yi为第i个样本的实际输出值。
第四,初始化天牛坐标。为了便于训练,天牛质心的初始坐标选[-1,1]的随机数组成,并将其保存在bestX中。
第五,比较。计算天牛在初始位置时对应的适应度函数值,将结果保存在bestY中。
第六,天牛左右须坐标位置更新。根据公式(4)更新天牛左须和右须的空间坐标。
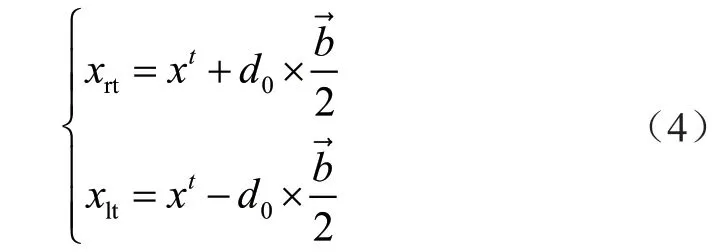
其中:xlt和xrt表示在第t次迭代时天牛左右须的位置坐标;xt表示天牛在第t次迭代时的质心坐标;d0表示天牛两须之间的距离大小。
第七,更新解。根据天牛两须的坐标,分别求左须和右须所对应的适应度函数值f(xrt)和f(xlt),根据公式(5)更新天牛的位置坐标。

计算在当前位置下天牛质心坐标对应的适应度函数值。若该值小于bestY,更新bestX和bestY。
第八,天牛须算法迭代停止。提前设置适应度函数值精度(本文取为0.000 001)和最大迭代次数(本文取为50),算法运行过程中,满足上述任意一个条件,即可下转至第九步,否则返回第六步继续运行。
第九,最优解生成。算法运行完成,bestX中存储的值就是本次天牛须搜索算法所寻找到的最优解,即待优化BP神经网络的初始权值和阈值。根据上述最优解初始化BP神经网络,导入训练数据进行BP神经网络的训练,最终训练出来的BP神经网络即为本文所提出的BAS-BP优化模型。图2为天牛须优化BP神经网络流程图。
2.3 BAS-BP模型与BP模型对比
根据仿真需要,本文的BAS-BP模型输出选为负载电流ia中的基波电流iaf,BAS-BP模型的输入选为负载电流ia、ib、ic和相对应的A相电源电压Ua,B、C相基波电流检测模型以此类推。参考文献[11]中的隐含层节点数量公式,BP神经网络的隐含层节点数设置为9个,因此对应的BP神经网络的结构为4-9-1。网络结构确定后,隐含层和输出层的传输函数皆选为默认的log sig和purelin函数。训练函数选为默认的trainlm[6]。关于模型的训练样本,本文用Simulink搭建了基于p-q算法的谐波电流检测模型,取p-q模型运行稳定后的数据作为训练样本。导入训练样本数据,在MATLAB中运行天牛须搜索算法。BAS算法运行结果如图3所示,图4为权阈值优化后的BP神经网络训练结果。

图2 天牛须优化BP神经网络流程图

图3 天牛须搜索结果
采用相同的样本数据训练一个权阈值随机的BP神经网络,其中BP神经网络的各项参数设置不变。为了更好地进行对比,随机权阈值的BP神经网络采用多次且分开的训练模式,训练的次数与BAS算法中的天牛迭代次数相同,取其中训练结果最优的作为最终的BP神经网络,最优训练结果如图5所示。

图4 BAS-BP训练结果
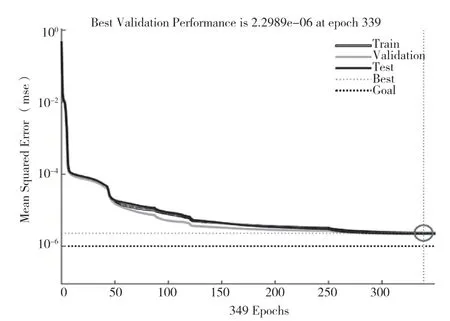
图5 BP模型最优训练结果
从图5可以看到:相比较于权阈值随机的BP神经网络,BAS-BP模型在训练过程中,针对训练样本所得的最小均方误差缩小了42.6%。将测试样本的2 000组数据分别代入BAS-BP模型和BP模型,BAS-BP模型预测得到的结果与实际样本数据的均方差为8.417×10-5,BP模型预测得到的结果与实际样本数据的均方差为2.175×10-4。相比较于BP模型,BAS-BP模型预测所得结果的均方误差缩小了约61.3%。由此可见,BAS-BP模型的精度明显优于权阈值随机的BP模型。
3 谐波检测方案设计
将训练好的BAS-BP模型应用于电力系统谐波检测,在Simulink中搭建一个如图6所示非线性负载仿真电路,电源频率设置为50 Hz,每个周期运行时间为0.02 s,系统运行时间设置为0.1 s。为了更好地体现BAS-BP谐波检测模型对于非稳态电力系统系统的适用性,三相电压源设置在0.06 s时产生幅值的突变,其中A相电源电压波形如图7所示。
利用gensim函数,将上述MATLAB中的BASBP模型和BP模型生成相应的Simulink仿真模块,并搭建了如图8所示的仿真,为了便于比较,仿真包含了BAS-BP谐波检测模块、BP谐波检测模块以及基于瞬时无功功率理论的ip-iq谐波检测模块。运行仿真,并将运行结果记录如下,通过观察图9、图10和图11,可以看到3种模型所测得负载电流中的基波波形大致相同,为此需要对图像采取进一步分析。

图6 三相电压源模块和非线性负载电路

图7 A相电源电压
将图9中4种模型所测得的基波波形分别进行FFT分析,并按照时间段记录各个模型的电流谐波总畸变率THD(Total Harmonic Distortion),结果如表1所示。
如图12所示,分析整个运行周期,在0~0.02 s和0.06~0.08 s两个阶段,BAS-BP模型测得的THD为3种模型中最小,且明显低于ip-iq模型,说明相对于ip-iq模型,BAS-BP模型的检测速度优势明显。在其余时间,BAS-BP模型测得的THD与ip-iq模型测得的THD大致相等,说明在电流稳定且模型运行稳定的情况下BAS-BP模型的精度与ip-iq模型精度相当。同时,在整个运行时间段,BAS-BP模型的THD都低于BP模型,说明了BAS-BP模型在谐波检测方面优于BP模型。
4 结 论
本文采用天牛须算法优化BP神经网络的初始权阈值,提高BP神经网络模型的精度,并将训练好的BAS-BP模型应运用电力系统谐波检测。通过仿真,证明了BAS-BP模型能够有效检测出电力系统中的基波和谐波。相比较于ip-iq模型,BAS-BP模型在保证了检测精度的同时,弥补了ip-iq模型检测速度上的不足,对于电力系统中非稳态电流的谐波检测,BAS-BP模型具有明显优势。但是本次方案也存在不足,BAS-BP模型的精度很大程度上受限于提供训练样本数据的p-q模型的精度,且本文的BAS-BP模型只能适用于训练时所采用的特定类型畸变电流对于实际电力系统中复杂多变的电流,不具有适用性。对此,可以把BAS-BP模型接入电力系统,电力系统运行时,将测量到的相关数据同时导入模型进行训练,通过不断地接收数据并进行训练,最终扩大BAS-BP模型的适用范围。

图8 系统仿真图

表1 4种模型所测得THD

图9 A相负载电流ia
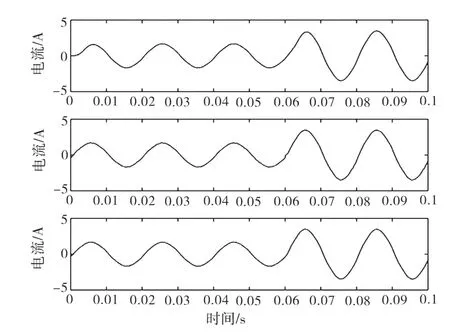
图10 ip-iq、BP、BAS-BP模型检测得到的A相基波电流
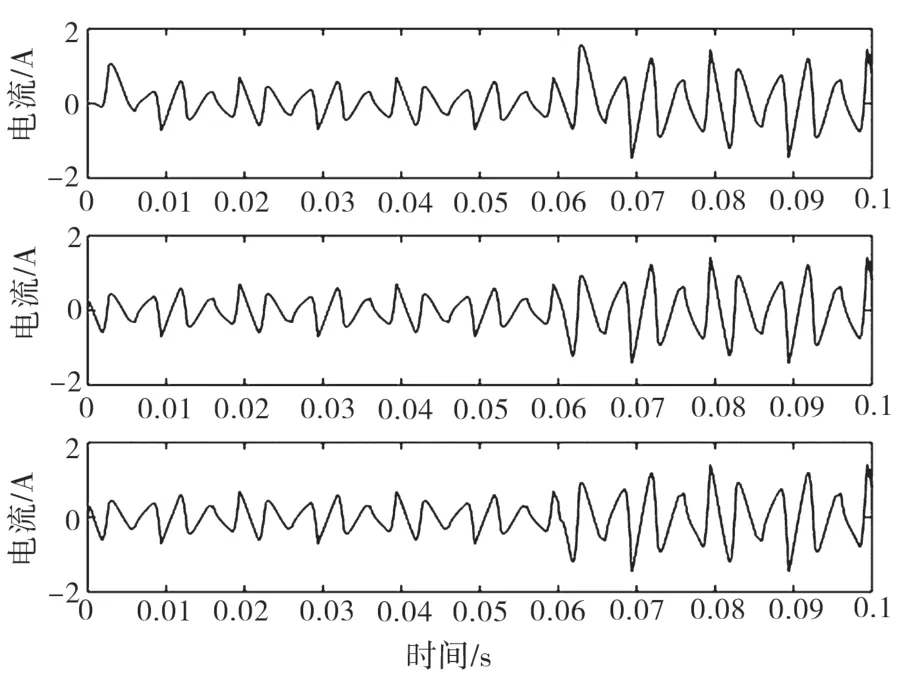
图11 ip-iq、BP、BAS-BP模型检测得到的A相谐波电流
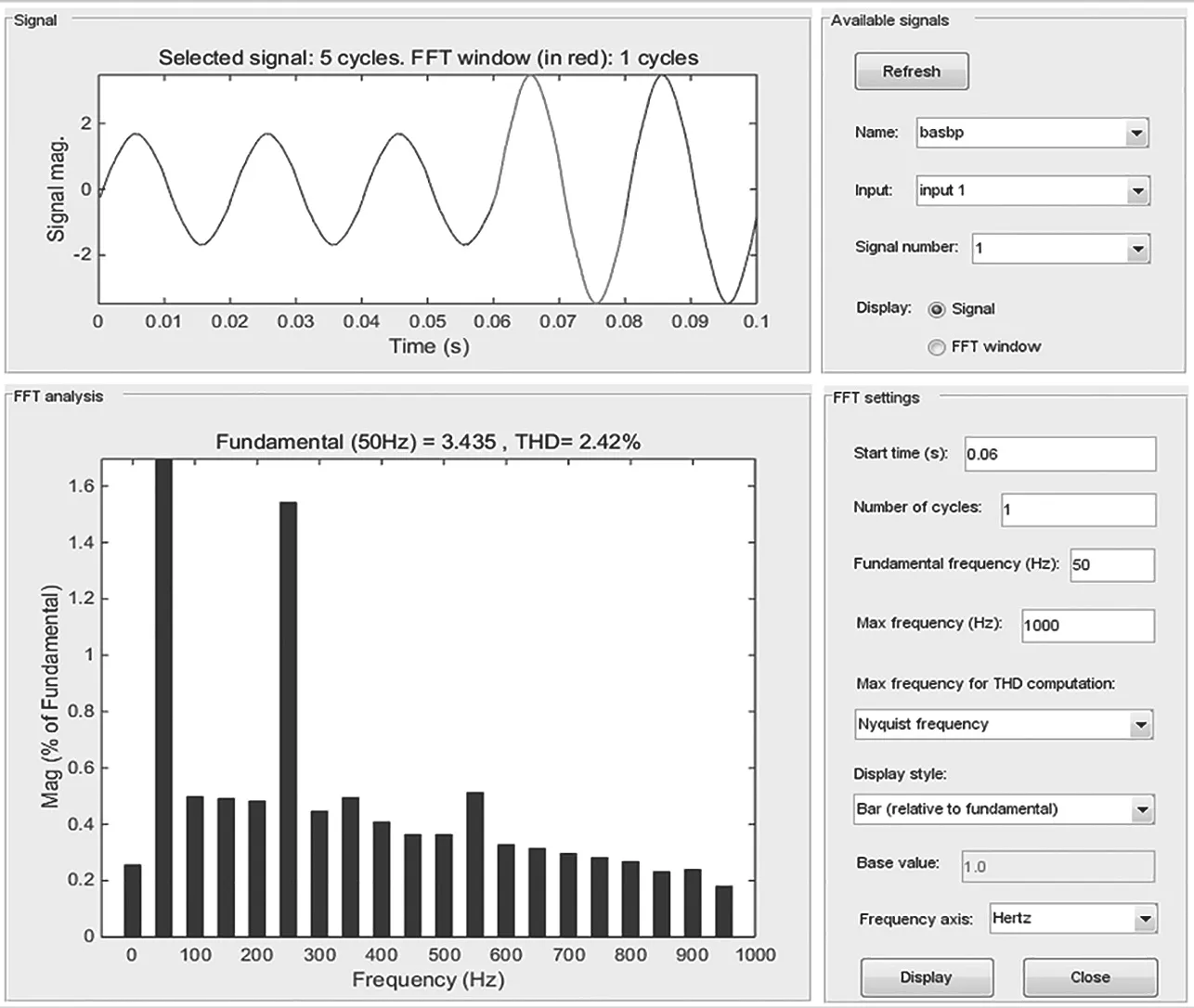
图12 BAS-BP模型所测得基波的部分FFT结果
