一种面向互联概率加权的JPDA多传感器数据融合方法

刘建锋

(1.南京航空航天大学电子信息工程学院,江苏 南京 211106; 2.雷达成像与微技术波光子技术教育部重点实验室,江苏 南京 211106)

0 引 言

联合概率数据互联(Joint Probabilistic Data Association, JPDA)是由Y.Bar-Shalom等人提出的一类使用概率加权进行目标-量测互联算法[1]。JPDA主要目标是实现面向密集杂波环境下多目标跟踪。多目标跟踪的主要困难在于求解杂波环境下对多个目标进行跟踪时出现的量测与航迹关联，其逻辑关系复杂，计算量大，多数情况下需要在复杂而庞大的搜索空间中寻找最优解或次优解。而求解这类问题，若不能利用固有知识来缩小搜索空间，就可能产生组合爆炸。Sittler教授[2]深入研究了数据关联技术，分析了数据关联实质，提出逆概率方法，得到了最优数据互联。最简单的数据关联技术是Singer等人[3]给出的最近邻(Nearest Neighbor, NN)方法。最近邻法是最早被提出的数据关联技术，其思想是选择唯一落在相关跟踪门内与被跟踪目标预测最近的回波作为关联对象，因此不适合密集多回波环境。何友等人[1]详细讨论了概率数据互联算法，该算法主要用于杂波环境单传感器单目标跟踪，与NN算法不同，不再以欧氏距离作为目标-量测关联准则，而是使用似然概率进行相应裁断，这能有效应对距离上相近杂波对关联的干扰。文献[1]同时给出了原始JPDA方法，将处于聚中的多个量测以概率加权形式关联至目标，使用多个量测估计同一目标状态，使得关联更具鲁棒性。据报道，这类方法已被应用于美国国家反导系统中。

1 相关工作

1.1 次优JPDA

因JPDA中数据互联计算较为复杂，不少文献讨论了次优JPDA快速方法。Roecker[4]将JPDA中传感器探测概率设为1，完全使量测与目标一一对应，类似Cheap PDA思路，使用二维分配方法，逐次生成似然概率由高到低的目标量测对，并设定适当阈值，低于门限的目标-量测对将在互联关系中被舍去，使在计算复杂性和精确性之间获得平衡。因互联事件生成的简化，降低了关联跟踪性能，因此，文献[5]中避开互联事件产生，可看成“最近邻”PDA方法实现，目标只选择与量测似然概率最高观测作为后验测量，并使用统计经验公式计算目标状态后验概率，但存在一定偏差。Zhou等人[6]和Fisher等人[7]都提出深度优先搜索法(Depth-First Search, DFS)产生可行互联事件，DFS是依据确认矩阵中行向量非0值进行搜索以此得出快速算法，但文献中给出的后验概率计算无规律可寻，只将概率计算分成直接法和近似法进行。

文献[8]推广了文献[6]的方法，提出使用分层法构造互联假设事件，将目标个数设置为对应编号层数，各层次搜索具有递归性并可独立进行。

1.2 避免航迹合并JPDA

为避免JPDA中航迹合并，Fitzgerald[9]提出了一种精确最近邻JPDA滤波，结合NN算法优点，除了最高概率数据互联假设外，其他所有互联假设被删除。Kastella[10]提出了一种称之为JPDA*的方法，使用统计领域平均场近似概念简化量测与目标间互联关系，并将由传感器量测引起的目标间跟踪误差精确建模，有效应对距离较近目标对的分离。文献[11]提出了一种去偏估计JPDA，在进行完一般JPDA估计后，去偏估计还将被进一步执行，确保所得估计无偏。而为应对目标个数事先未知的跟踪问题，同时避免使用复杂随机有限集技巧，Svensson等人[12-13]给出了集合JPDA方法和基于Kullback-Leibler分割的Kullback-Leibler集合JPDA。

集合JPDA引入最优子模分配(Optimal Subpattern Assignment, OSPA)来衡量估计值与状态空间值间差异程度，具体如式(1)所示：

(1)

1.3 多传感器数据融合

文献[14-15]使用卡尔曼滤波给出了基于JPDA的多传感器数据融合。Lyu等人[16]使用拉格朗日松弛法提出了基于JPDA的串行和并行多传感器数据融合，并用多维分配方法实现了这一仿真过程。Lyu在文中将多传感器数据融合，寻优m个最优互联事件认为是一类m最优(N+1)-D分配问题，可以使用多项式时间加以解决。每一互联事件θ可以使用广义似然比分配一个代价量测公式，如式(2)所示：

(2)

(3)

其中Ξ指所有可行互联事件空间，包含所有可行互联事件θ，θ∈Ξθ(1)表示在可行互联事件空间Ξ中去掉θ(1)后的情形。

式(3)中优化表示(N+1)-D分配问题，这就使用(N+1)-D分配获得了m个最优多传感器融合互联事件，使用连续拉格朗日松弛技巧可以在多项式时间内获得问题解。式(3)最差情形下，计算复杂度为O(m(N+1)ρL4)，L为互联事件θ中(N+1)元组个数，ρ为单个(N+1)-D分配中松弛周期数。通过预处理和最优化技巧操作，复杂度可降为O(m(N+1)ρL3)。

何友等人[17]从Reid提出的原始MHT方法出发，提出了一类基于多假设跟踪的多传感器数据融合方法。Coraluppi等人[18]以被动多声呐为平台，给出了一类多传感器多假设跟踪算法，对各平台中的MHT进行分布式处理，总体融合达到了近乎实时效果。文献[19]以有源和无源传感器为基础，通过主被动传感器量测并行处理提升了多传感器MHT跟踪性能，同时，系统间协调提升了目标跟踪距离分辨率。

以上所述单传感器JPDA在现今复杂电磁环境下，若要符合射频隐身要求，则不能较好跟踪多个目标。同时，文献[14-19]提出的方法具体实现有些困难，不便于编程仿真。在这一背景下，本文基于Shalom等人给出的单传感器JPDA思路，使用单传感器目标-量测互联概率作为加权因子给出了一种多传感器数据融合方法，并且仿真了本文JPDA在不同杂波密度、观察和过程噪声下目标跟踪距离RMSE性能，使用数据集PETS2009，仿真对比了本文2类多传感器JPDA与其他跟踪方法在行人跟踪方面的性能。

本文JPDA与文献[1]中JPDA不同之处：原始JPDA遍历了各个目标-量测互联事件，本文使用集成线性规划法(Integer Linear Program, ILP)获得m个最优互联事件，以此计算目标状态估计。本文多传感器JPDA与文献[16]不同之处：文献[16]中使用多维分配获得多传感器多目标状态估计，计算量较大，当被跟踪目标超过10个，将难以达到计算实时性要求；本文使用概率统计加权获得的多传感器数据融合方法，计算复杂度随跟踪目标个数增长而线性增加。

2 单传感器联合概率数据互联

2.1 联合概率数据互联算法基本模型

假设在杂波中跟踪T个目标，在离散时间间隔上获取观测，每个观测都由几个量测(也称为探测报告或者回波)组成。有些量测源于目标，有些量测源于杂波，有些目标也许在某一特定时刻上根本不产生任何量测。

(4)

设mk为k时刻跟踪波门中的确认量测数，于是Bayes框架下跟踪模型量测方程表示为：

(5)

2.2 互联事件生成及概率计算

(6)

1)每一量测(除虚警外)至多被分配给一个目标；

2)每一目标只能分配给一个量测。

互联事件空间可以被表示为如下形式两元向量集合：

(7)

其中，|Θ|=nk为总的分配事件个数，θ∈Θ⊆ΒN×(M+1)为一个可能的数据互联两元向量。

(8)

(9)

2.3 JPDA快速实施

传统JPDA计算量巨大，公式(8)中所有可能互联事件求和量存在潜在性爆炸，快速实施方法是使用m个最优概率假设近似qk(·)，在总的概率计算中仅有较小部分概率遗失：

(10)

使用最小化代价函数重写数据互联事件：

(11)

(12)

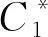
(13)

3 基于互联概率加权的JPDA多传感器数据融合

多传感器、多目标跟踪问题是在杂波中用Ns个传感器跟踪T个目标。来自这些传感器的量测在离散时间间隔上由一个中心处理器接收处理。每个传感器量测最多可能来自一个目标。有些目标也许在一个特定时间区间里或对某一特定传感器根本不提供任何测量，同时，假定来自某一传感器的量测误差与来自其他传感器量测误差统计独立。

多传感器联合概率数据互联算法有2种处理结构，一种为并行处理结构，另一种为序贯处理结构。

3.1 基本模型描述

设k时刻来自传感器i(i=1,2,…,Ns)的确认报告数为mki，传感器间量测误差统计独立，量测方程统一表示为：

(14)

Ns个传感器在k时刻的组合观测向量为：

(15)

相应标号集合为：

{{0,1,2,…,mk1},{0,1,2,…,mk2},…,{0,1,2,…,mkNs}}

考虑1对Ns映射：

(16)

式(16)表示目标t(t=1,2,…,T)在k时刻与Ns个传感器的一组回波互联关系。每个映射ams包含Ns个映射ai:{1,2,…,T}→{0,1,2,…,mki}，ai表示目标t在k时刻与传感器i的某个回波互联，如果映射到“0”，则说明传感器i在k时刻没有回波与目标t互联，这样就包含了由于漏测引起的不完整测量与目标互联情况。

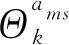
(17)

(18)

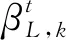
多传感器联合概率数据互联事件的概率由式(19)给出：

(19)

由于假定各传感器间测量误差相互独立，因而有

(20)

把式(20)代入式(19)，并进行适当变换得到：

(21)

3.2 并行多传感器联合概率数据互联

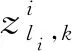
目标t在k时刻状态估计表示为：

(22)

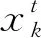
(23)

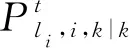
并行多传感器联合概率数据互联方法实施步骤如下：

步骤2检测聚中是否存在观测，若无，则执行步骤8；否则，执行步骤3。

步骤3由聚中量测Zk和观测预测位置，获得确认矩阵Ω。

步骤4对于Ω，基于JPDA的2个基本假设，计算互联矩阵ω，形成nk个联合事件。

步骤5由联合事件计算互联事件θ，如式(24)。

(24)

步骤6由互联事件θ计算目标-量测互联概率βjt，再由卡尔曼滤波获得各观测下目标状态估计和误差协方差。

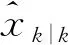
步骤8传感器未探测到目标，此传感器不参与融合。

步骤9各传感器并行执行步骤1～步骤8，并将各传感器步骤7所得结果传送至融合中心融合，得到多传感器融合结果。

3.3 序贯式多传感器联合概率数据互联

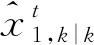
(25)

其中：

(26)

且有：

(27)

协方差矩阵的更新方程是：

(28)

(29)

(30)

序贯多传感器联合概率数据互联方法实施步骤如下：

步骤1第1个接收到量测的传感器，输入其观测Zk={z1,z2,…,zk}以及被跟踪目标预测位置，由Bayes模型计算跟踪门聚。

步骤2检测聚中是否存在观测，若无，执行步骤9；否则，执行步骤3。

步骤3由聚中量测Zk和观测预测位置，获得确认矩阵Ω。

步骤4对于Ω，基于JPDA的2个基本假设，计算互联矩阵ω，形成nk个联合事件。

步骤5由联合事件计算互联事件θ。

步骤6由互联事件θ计算目标-量测互联概率βjt，再由卡尔曼滤波获得各观测下目标状态估计和误差协方差。

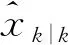
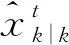
步骤9传感器未探测到目标t，此传感器不参与融合。

4 数值结果

4.1 单传感器JPDA算法仿真与分析

图1 目标a与b实际位置

图2 目标观测数据、杂波以及滤波后的估计位置

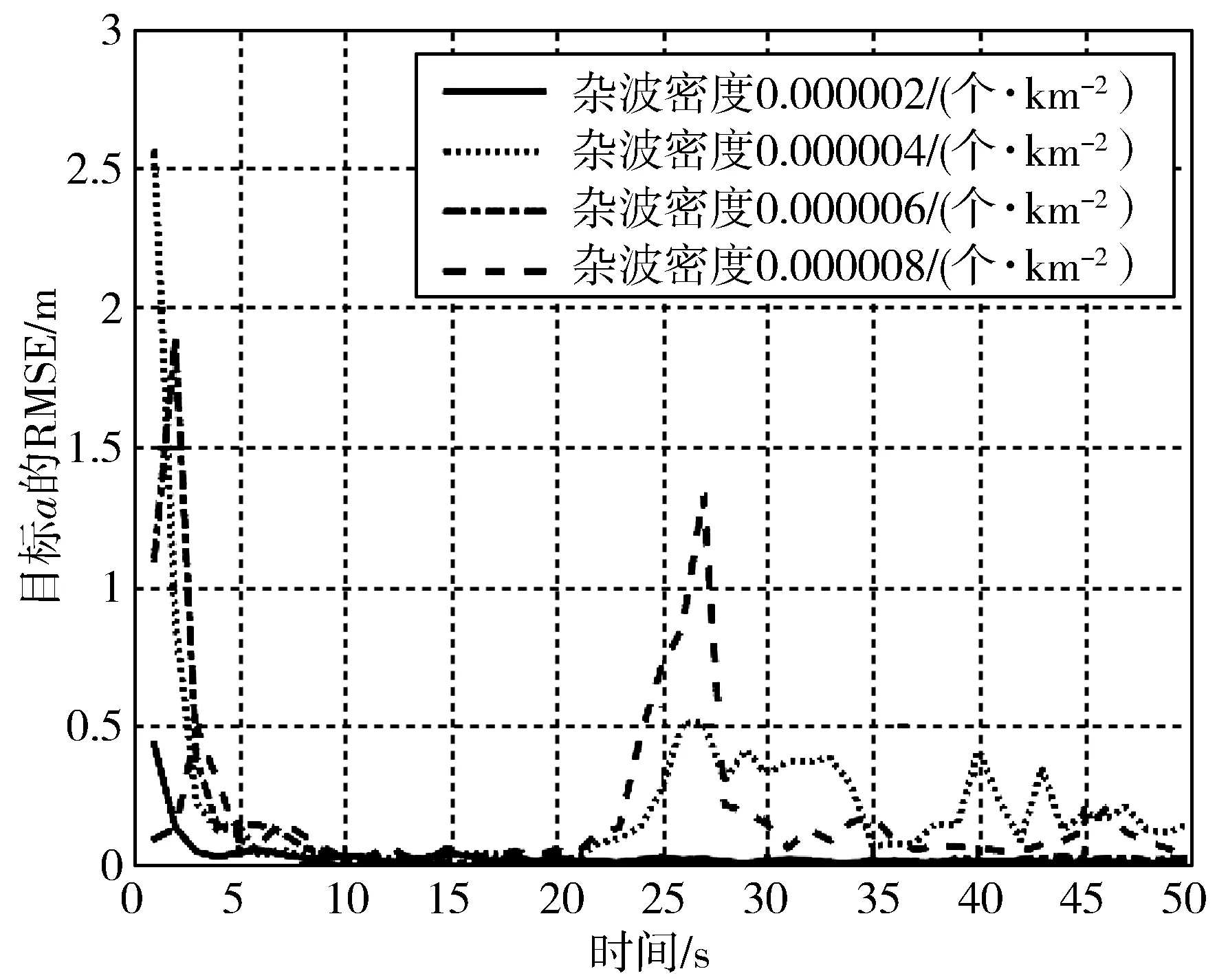
图3 目标a在不同杂波密度λ下的距离RMSE

图4 目标b在不同杂波密度λ下的距离RMSE

表1给出了不同杂波密度λ下JPDA跟踪目标的距离RMSE。

表1 不同杂波密度λ下JPDA跟踪目标的距离RMSE

实验结果分析：从图3、图4以及表1总的趋势来看，随着仿真场景中杂波密度λ升高，目标a和b的平均距离RMSE增大，这与实际主观感觉一致，杂波密度增大，导致被跟踪目标中出现非物理目标，影响真实目标跟踪精度，必然导致跟踪误差增大，本文从程序仿真上使得这一认识得以具象化。

同时，由仿真图可以看出，随着杂波密度增加，跟踪目标的距离RMSE收敛时间增长。图3中，当杂波密度为0.000008个·km-2时，目标a在26 s时出现了RMSE波动，RMSE突然增大，并在随后时刻，这一走势仍收敛得不特别彻底。图4中，当环境杂波密度为0.000006个·km-2时，目标b在12 s、15 s、30 s和32 s皆出现距离RMSE大波动，并在15 s后，这一波动仍在较高位点起伏，未出现收敛迹象。这启示系统设计者

图5 目标a在不同过程噪声方差下的距离RMSE

在构造总体跟踪体系时，当环境杂波出现较高值时，一定得进行相应预处理。

图5给出了不同过程噪声方差(以协方差矩阵对角元素q11和q22表征这一参数)下目标a的距离RMSE，图6给出了不同过程噪声方差下目标b的距离RMSE。

图6 目标b在不同过程噪声方差下的距离RMSE

表2给出了不同过程噪声下JPDA跟踪目标的距离RMSE。

表2 不同过程噪声下JPDA跟踪目标的距离RMSE

实验结果分析：从图5、图6以及表2来看，随着仿真中过程噪声协方差对角元素增大，目标a和b的平均距离RMSE增大，这符合实际认知，因为过程噪声增大意味着目标运动方程建模模糊性增大，模型中被跟踪目标运动波动起伏变大，导致跟踪距离误差增大，此处仿真恰好验证了这一看法。

同上收敛性分析，但过程噪声增大对收敛情形影响较小。图5中，过程噪声对角元素为3，目标a在47 s时，出现了一次起伏，其他过程噪声情形和时间段上，收敛效果较好。图6中，目标b在过程噪声对角元素在4.50 s时，出现了一次较小波动，其他噪声水平下和时间段收敛效果较好。这意味着，考虑综合成本以及系统实现上，可适当放宽系统运动方程建模要求。

最后，在不同观测噪声情形下，图7和图8给出了跟踪目标a和b的距离RMSE。

图7 目标a在不同观测噪声方差下的距离RMSE

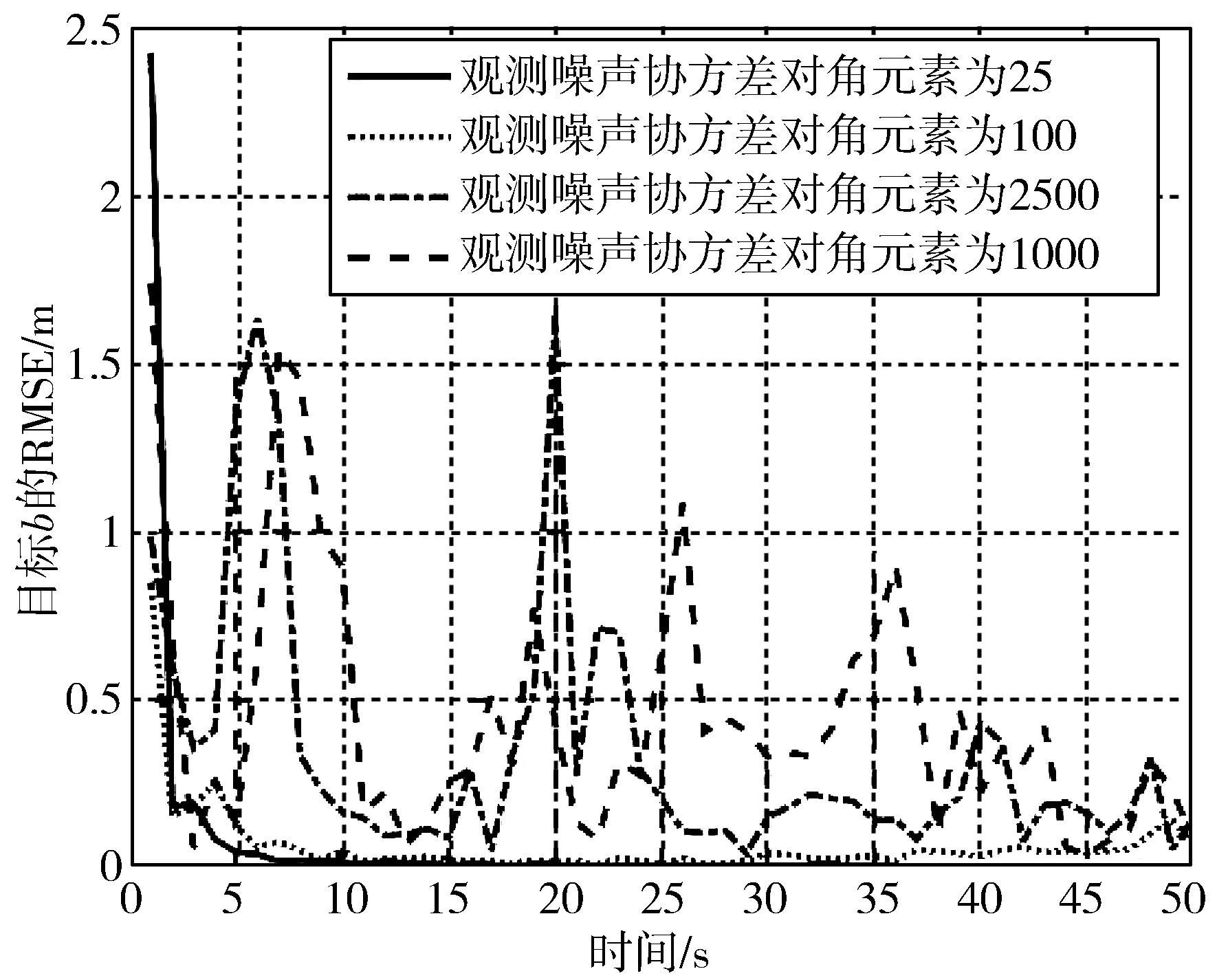
图8 目标b在不同观测噪声方差下的距离RMSE

表3给出了不同观测噪声下JPDA跟踪目标的距离RMSE。

表3 不同观测噪声下JPDA跟踪目标的距离RMSE

实验结果分析：从图7、图8以及表3来看，随着仿真中观测噪声协方差对角元素增大，目标a和b的平均距离RMSE增大，这与主观感觉也一致，观测噪声协方差增大，导致对被跟踪目标量测不确定性增大，量测浮动增大，量测波动使得跟踪距离误差增大，本文仿真恰好验证这一观点。

同样，由图7和8可以看出，随着观测噪声增大，目标跟踪距离RMSE收敛变慢，并且在较高观测噪声情形下，基本处于波动状态，未达到严格收敛状态。目标a在观测噪声协方差对角元素为10000时，分别在21 s和37 s出现了较大波动；当对角元素为2500时，在14 s、27 s、36 s和45 s时，也出现了较大峰值。目标b在观测噪声对角元素为10000时，在26 s、36 s时，出现较大峰值，波动情形严重，未处于严格收敛状态。这要求在设计该类系统时，传感器选择应格外注意，较差传感器在观测过程中观测噪声大，跟踪目标的RMSE起伏较大，会迟迟得不到收敛结果。

4.2 多传感器JPDA与其他跟踪方法性能比较

将本文多传感器并行式和序贯式JPDA方法应用于计算机视觉跟踪，使用数据集PETS2009中具有较高目标密度的S1L1-2和S1L2-1部分。PETS2009-S1L1-2包含241帧图像序列，帧率约为7帧/s，并且行人运动为线性模型，恰好契合本文JPDA运动模型。S1数据集中，40个行人占据约10 m2地面，人均占地面积0.25 m2。

处理前，首先，获得数据集S1L1-2中R0、R1和R2区域各帧人群密度。图9描绘了区域R0、R1和R2覆盖情形。图10展示了具有代表性的帧，序列中给出了矩形人群移动情况。表4给出了3区域位置覆盖左上角和右下角的坐标。

图9 区域R0、R1和R2

图10 S1L1-2中第0、50、100和150帧(左上至右下)

表4 3区域位置覆盖左上角和右下角的坐标

图11给出了数据集S1L1-2具有代表性的帧，显示了目标人群在较为密集环境下的移动情况。

提取出数据集PETS2009 S1L1-2和S1L2-1中前8帧左右行人运动位置和速度信息用于本文JPDA初始化，再使用本文JPDA方法跟踪目标，各帧图像序列信息即为目标真实运动轨迹，并使用如下指标衡量JPDA跟踪效果。

4.2.1 性能指标

示例中，使用恒速模型。给出如下性能衡量指标，MOTA：多目标跟踪精确性；FP：绝对虚警；FN：相对虚警；IDs：目标错误互联个数；MOTP：多目标位置精度跟踪准确性；ML：航迹遗失率；MT：航迹维持率；GT：地面真实航迹。

(31)

(32)

(33)

(34)

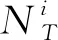
4.2.2 实验结果与数据分析

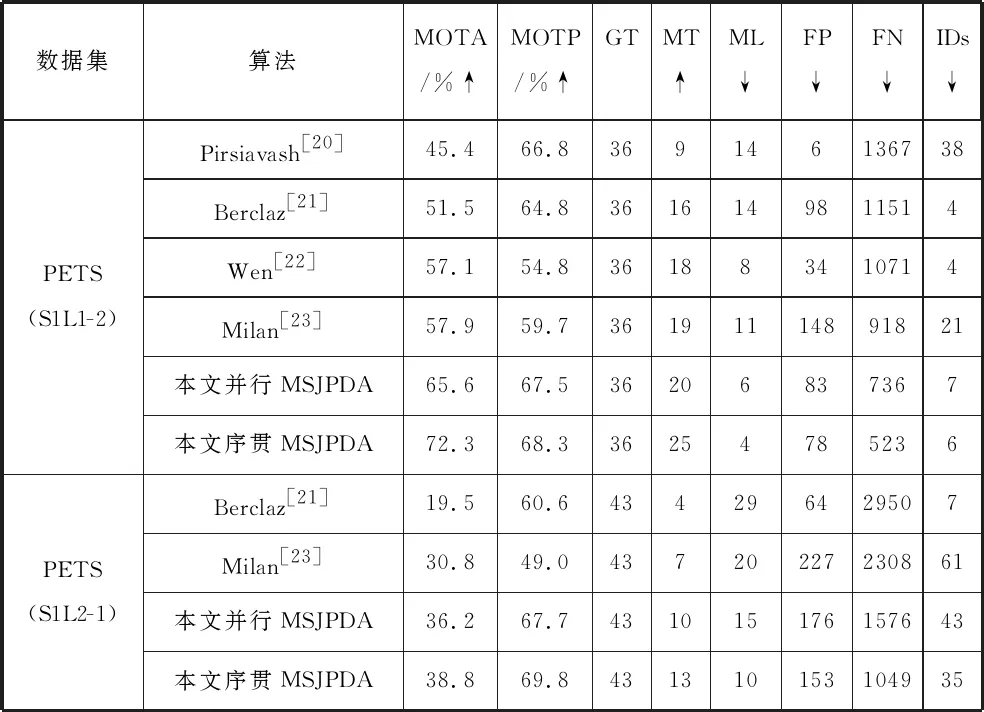
表5 各算法性能比较

表5中向上箭头↑表示数值越大越好，向下箭头↓表示数值越小越好。

实验结果分析：就数据集PETS2009(S1L1-2)而言，序贯多传感器JPDA方法在MOTA性能上获得了72.3%最优表现，这说明跟踪目标准确个数最优，并行多传感器JPDA方法在这项指标上数值为65.6%，其他几类方法性能结果估计在50%～60%之间；同时，在MOTP上，序贯多传感器JPDA结果为68.3%，并行多传感器JPDA这项指标结果为67.5%，表征对多目标跟踪位置精确性最好；在MT和ML这2项性能上，皆获得了最优表现，序贯多传感器JPDA的MT值为25，ML值为4，并行多传感器JPDA的MT值为20，ML值为6；而关于MOTA分指标，FP和IDs获得了良好结果，意味着对虚警和目标辨识有较好效果，两类多传感器JPDA的结果基本都处于中间位置；序贯多传感器JPDA在FN上获得了523数值，漏检个数最少，为最优结果，并行多传感器JPDA这项指标为736。关于数据集PETS2009(S1L2-1)，序贯多传感器JPDA在MOTA性能上获得了38.8%最优表现，并行多传感器JPDA结果36.2%；在MOTP上，序贯多传感器JPDA的结果为69.8%，并行多传感器JPDA这项结果为67.7%，分别为最优和次优；在MT和ML这2项性能上，2种方法结果仍为最优和次优；而在FN上，结果也最好。这说明多传感器JPDA相较于其他方法，显著地提升了跟踪性能，并且在这2类多传感器JPDA中，序贯式融合略优于并行式多传感器JPDA方法。

5 结束语

针对单传感器JPDA不能较好解决复杂环境下多目标跟踪问题，本文使用单传感器JPDA目标量测互联概率作为权重因子，给出了基于JPDA的并行式和序贯式多传感器数据融合方法，提高了跟踪精确性和鲁棒性，并仿真了本文JPDA在不同杂波密度、过程和观察噪声下目标跟踪距离RMSE，结果表明，随着这3项指标增大，跟踪目标距离RMSE之和增大。在数据集PETS2009下，比较了本文2类多传感器JPDA与其他几类跟踪方法就行人跟踪的性能，在PETS2009S1L1-2下，序贯式多传感器JPDA相较于其他方法在跟踪准确性上提升了约26.69%，并行式多传感器JPDA相较于其他方法在准确性上提升了19.21%左右。航迹维持、航迹遗失结果皆为最优。综合各项跟踪指标来看，多传感器JPDA方法优于其他算法，并且，序贯式多传感器JPDA获得了最优性能。