利用抗假频凸集投影算法的规则缺失地震数据重建
2020-08-18张恒琪张博泓
刁 塑 张 华 张恒琪 张博泓 余 政 庞 洋
(东华理工大学放射性地质与勘探技术国防重点学科实验室,江西南昌330013)
0 引言
在地震数据现场采集中,由于需要考虑客观存在的障碍物、禁采区、海洋拖缆羽状漂移和采集经济成本等因素,地震数据沿空间方向通常呈现不规则分布或规则缺失分布;在地震数据预处理中,必要的剔除废炮、废道等操作也会导致地震道缺失。而后续的常规数据处理,如速度分析、叠加、偏移等,应建立在完整的地震数据基础上。因此,亟待探寻可行的重建完整数据的方法。
现行的地震数据重建算法可分为四大类:①基于滤波器方法[1],主要是依据建立卷积插值滤波器实现数据重建;②基于波场延拓算子重建方法[2-3],如常见的利用Kirchhoff积分算子;③基于快速降秩插值方法[4-6],即是将插值问题转化为图像填充问题;④基于数学变换方法,如常用的傅里叶变换、拉东变换、小波变换、曲波变换等,先变换到数字域进行处理,再反变换回时空域[7-14]。本文方法属第四类,即通过改进算法,在重建的同时消除伴生假频。
空间均匀网格下缺失的地震数据分为规则缺失和非均匀缺失。一般非均匀缺失数据转换到频域,它引起的假频信息转化为低幅值不相干随机噪声,可设置其阈值门限,通过稀疏迭代去噪法进行消除。而规则缺失数据在频域中产生的假频与真实频谱相近,基于传统的迭代稀疏促进求解方法很难取得高分辨率、高保真、高信噪比的重建结果。为此,人们提出了较多数据重建方法以压制假频干扰,如倾角扫描法,此类方法需先扫描同相轴倾角[15],然后沿倾角方向加权、内插地震道;Sinc地震道插值方法[16]是对满足采样定理的数据做加密采样点处理,不需获取同相轴倾角,运算速度快,但无法正确内插含有空间假频的地震道;小波变换地震道插值方法是利用小波变换的时频分析特性[17],多级重构实现地震道插值,但该插值算法较复杂,且精度较低。
对于不规则空间带限二维地震数据,结合非均匀快速傅里叶变换和最小二乘反演算法,都取得了较好的重建效果[18-23];此方法也可应用于规则欠采样数据中,但其抗假频效果欠佳,且不能有效区分真实频谱与假频信息。凸集投影(Projection onto convex sets,POCS)算法对于随机的和规则的欠采样数据都能重建出完整数据[24-25],但对规则缺失较严重数据,此方法去假频效果不甚理想。在f-k域由规则采样引起的假频幅值与真实频谱相近,为了进行区分,需对整个频域范围内所有频率进行搜寻。在信号分离和插值方面,与τ-p域相比,f-k域简捷有效,主要是因为τ-p重建方法计算量大,且重建效果不如f-k域方法,尤其对低信噪比数据[26]。同时,f-k域方法可利用所有期望频率的信息对缺失数据施行稳定的插值和去噪。
本文采用傅里叶变换,在传统POCS方法中引入Naghizade[27]提出的选择函数,以去除规则欠采样引起的假频信息。将此方法应用于理论数据和实际资料处理,均取得了较理想效果。
1 方法原理
1.1 建立选择函数
首先对所有频率或在任意频率范围内进行扫描搜索,以确定主要能量的斜率或路径。
设d(t,x)为原始地震数据,D(f,k)为其相应的f-k域振幅谱。为了简化,将频率和波数做归一化处理,令时间轴和距离轴上采样间隔都为1,且f-k频谱关于频率轴对称,只需考虑正频率的频谱,得到归一化频率范围f∈(0,0.5)、归一化波数范围k∈(-0.5,0.5)(图1)。设定每条角度射线起始位置为频域原点(f,k)∈(0,0),从图1看出,可沿着角度射线方向求取射线上振幅能量之和。

图1 f-k域角度射线扫描示意图
则每条射线所扫描的能量值为

式中:p为角度射线扫描斜率,其取值范围依据不同数据的频谱分布而定;n为归一化频率f的索引;算子表示沿数值较小方向取整数值。在某一区间,若p值对应的函数M值大于邻近值,则称M为该范围对应的峰值。而在实际处理过程中,对于诸多峰值,可通过设置阈值的方法,识别函数中的几个较主要峰值,代表主要反射波同相轴的振幅。假设已识别L个峰值,如p1,p2,…,pL。
第二步,依据函数M(p)的峰值和扫描斜率范围,初始化一个零矩阵H,其维度与数据频谱维度相同,目的是把p1,p2,…,pL射线上反射波能量准确分配到矩阵H中(令L个角度射线上的值为1,其余各处为0)。则有
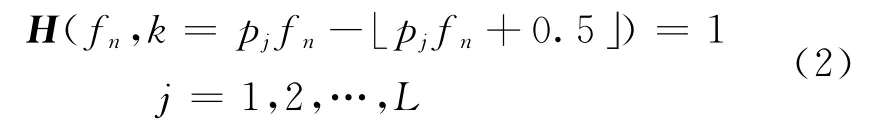
式中:j为角度射线p的索引;n、f、k同式(1)。
最后,考虑到邻近各角度射线两侧的能量应为同相轴能量,为拾取更完整同相轴信息,将所得H与一维方脉冲函数B(1,Lb)做卷积,沿波数轴方向拓宽每个角度射线,最终得出选择函数

式中:Lb是函数B沿波数轴方向上的长度,代表各个角度射线扫描的宽度,且函数B沿频率轴方向无值。从式(2)和式(3)可知,在选择函数W中,任何大于1的值都设定为1,小于1的值都设为0。
1.2 POCS算法
传统POCS重建方法的迭代表达式为
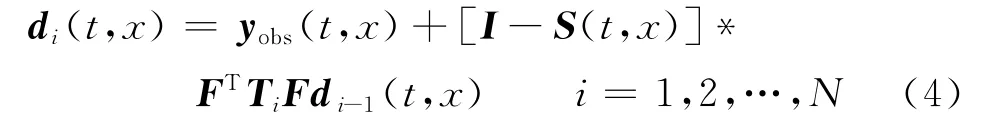
式中:di(t,x)为第i次迭代所得重建数据;I为单位矩阵;yobs为原始数据,即d0(t,x);F和FT分别为傅里叶正、反变换算子;N为满足精度要求时最小迭代次数;S(t,x)为采样矩阵;Ti为硬阈值算子,满足

式中:ci表示第i次迭代得到的傅里叶系数,满足ci=Fdi(t,x);λi表示第i迭代的阈值,本文选用的阈值[28]为
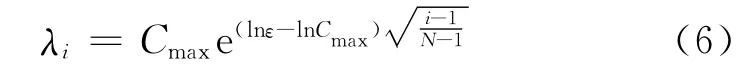
式中:Cmax为傅里叶系数最大值;ε为靠近零的正值,不同数据ε值有所差别,与数据中噪声能量有关,计算中通过多次测试人工选取。
为体现本文阈值参数的优势,将其与文献[28]中的线性阈值与指数阈值做重建对比,其重建后的信噪比公式采用,其中x0表示原始模型数据,x表示重建结果。显然信噪比越高,表明重建效果越好。计算结果如图2所示。可见在取得相同信噪比情况下,本文阈值参数所用迭代次数少,计算效率高;在相同迭代次数下,本文阈值参数重建信噪比最高。因此,本文阈值明显优于线性阈值和指数阈值。

图2 不同阈值函数重建结果的信噪比曲线
将选择函数W代入到传统的POCS迭代重建过程中,即把式(3)代入式(4)中,最终的抗假频POCS重建算法为
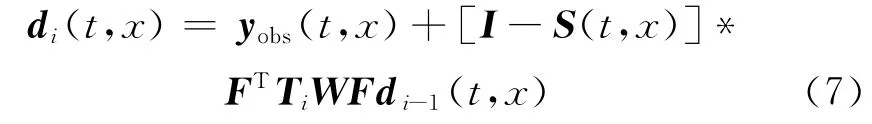
选择函数W能消除规则欠采样产生的假频干扰,使每次迭代过程中有效波能量聚焦,因此修改后的POCS算法能成功地重建规则缺失道。
2 数值模拟
采用主频为40Hz雷克子波合成81道地震记录(图3a),每道501个采样点,该记录总共有3个地震反射同相轴,采样间隔为2ms,道距为5m。
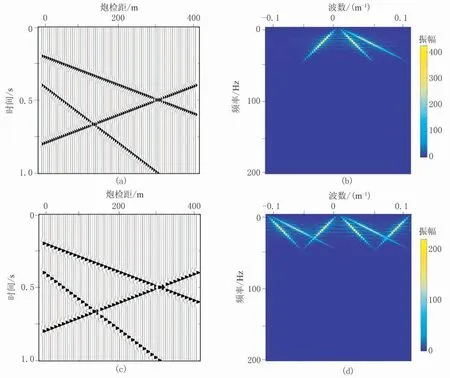
图3 原始模型采样及其f-k谱
为了更清晰地验证本文抗假频重建方法的可行性,本文通过对比重建后的振幅谱观察假频是否消除,并对比重建后的信噪比。首先,对模型数据(图3a)进行50%规则欠采样,即去除偶数道数据,只保留奇数道数据,得到欠采样数据(图3c)及其频率谱(图3d)。可明显看到,在对应f-k域中(图3d)因规则欠采样导致的假频与真实频谱(图3b)较接近。因此,在之后的重建过程中,需消除假频的影响,这样最终才可得到完整而规则的地震数据。
为验证本文方法的有效性,首先采用传统傅里叶变换和POCS算法进行重建,选择迭代次数N=20,阈值函数中的ε值为0.001。观察重建的结果(图4a)及其对应的振幅谱(图4b),可见图4a中偶数道上有效波能量并未得到任何恢复、在图4b中假频仍然存在,且重建结果的信噪比为2.7dB,说明传统方法无法重建缺失地震道。
再采用本文抗假频的POCS算法进行重建,选定与传统重建相同的参数和迭代次数。依据方法原理,选择函数以图3d中的原点为起点,对频域中的能量进行扫描,保留3个能量峰值对应的倾角,并在波数方向拓宽扫描范围,利用式(7)得到无假频的重建数据。观察此时所得重建地震数据(图4c),其偶数道得到很好的重建,同相轴连续完整;且对应振幅谱(图4d)上也完全看不到假频信息。对比图4d与图3b,表明本文所提抗假频POCS算法能有效地重建出规则缺失的地震道数据,且消除了规则欠采样所导致的假频,重建结果的信噪比增至14.5dB。
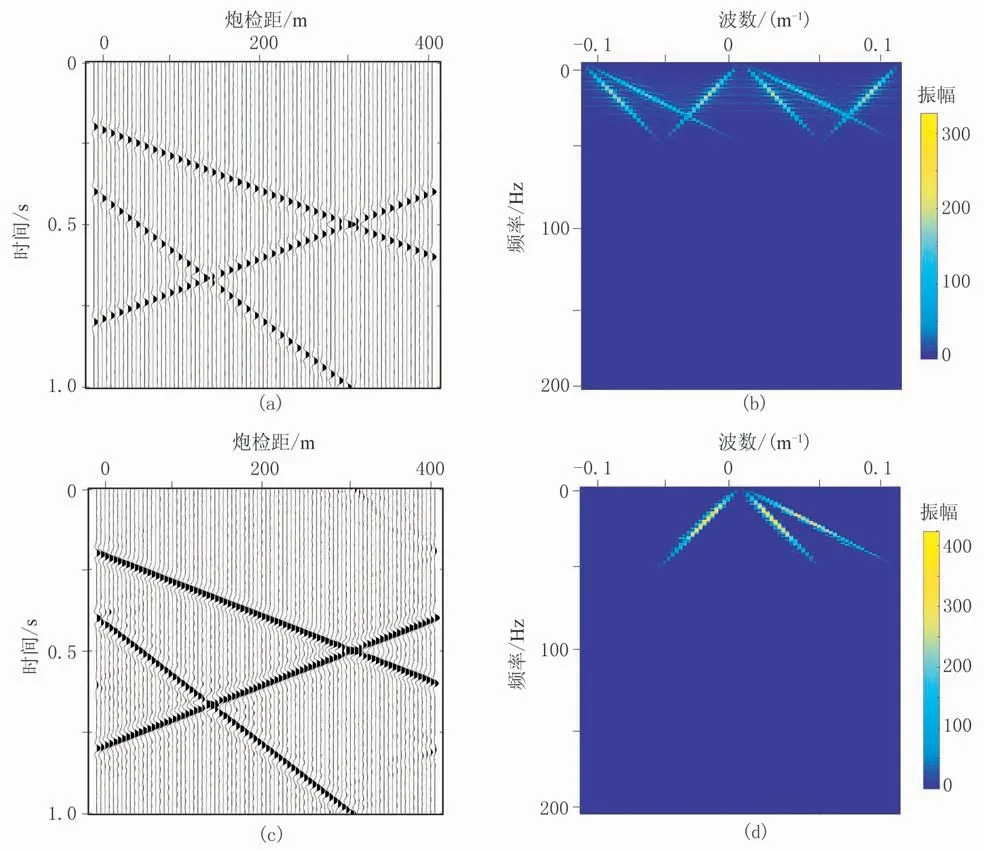
图4 两种重建方法对比结果及其f-k频谱
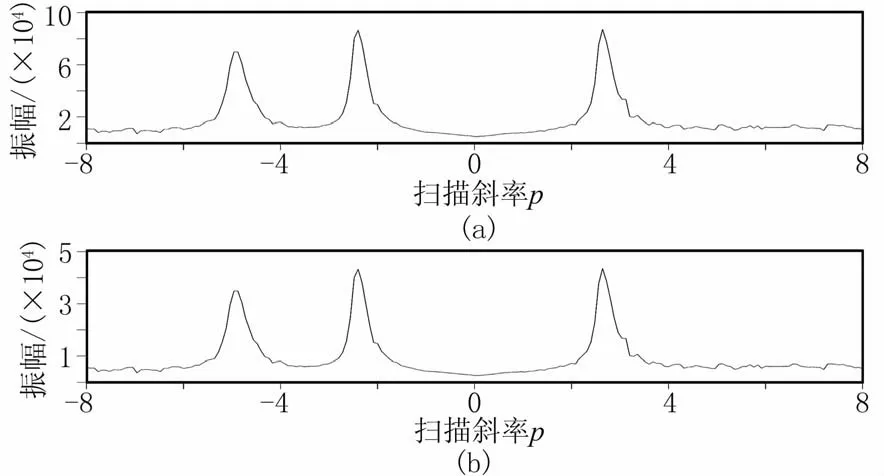
图5 M(p)范围内能量分布图
详细展示本文方法如何得到图4c重建结果。首先,利用式(1)分别求取原始数据和规则缺失50%数据对应的M(p)峰值(图5),扫描斜率p的范围设为-8~8,对比图5a与图5b,其主要能量峰值对应的p值一致。依据峰值范围,设定合适阈值,保留对应同相轴频谱的3个峰值,并分配到矩阵H中,再利用式(3)建立选择函数,结果如图6。其中大于阈值区域的值为1,小于阈值区域的值为0。可知图6b中选择函数与图6a选择函数能量分布一致,说明选择函数识别出了真实频谱。然后将该选择函数引入到POCS方法中,使得在每次POCS算法迭代过程中,该选择函数可很精确地拾取真实频谱,再参与下一次迭代计算,使得原始信号频谱能很快聚焦。
为更进一步验证本文方法的可行性,针对原始模型数据进行25%规则采样,即得到规则缺失75%数据(图7a)及其对应的频谱(图7b),可见真实频谱与假频信息相互交错缠绕,且能量非常相似,传统方法很难去除假频信息。采用本文方法,选定合适的迭代次数和阈值参数ε值,得到重建结果(图7c)及对应f-k谱(图7d)。该重建结果的信噪比为8.7dB。
分析重建结果的f-k谱(图7d),本文引入的选择函数在重建过程中有效地压制了假频干扰,保留有效波能量。同时从建立的选择函数(图6c)中可见,同相轴能量对应的峰值与图6a一致。但相比之下,其75%规则缺失数据重建效果较差,说明当缺失较为严重时,重建结果则难以达到理想效果,周边已知的地震道不足以恢复大范围连续缺失的地震道,因此需发展高维的重建方法,从另一维度进行重建。同时需说明的是,因基于傅立叶变换的二维重建方法只能处理近似线性同相轴,而对于非线性同相轴则需做分窗口重建,使其满足近似线性同相轴的要求。
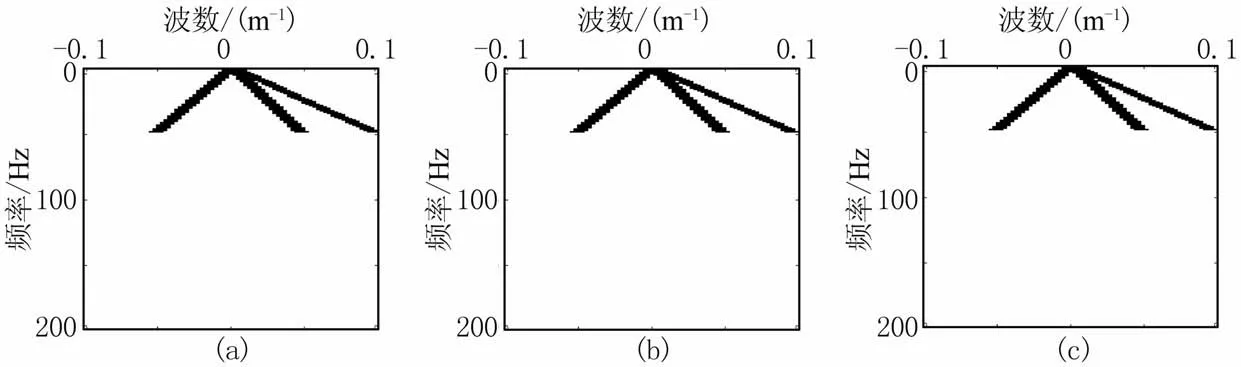
图6 f-k域选择函数值

图7 25%规则采样重建结果及其f-k谱
3 实际数据算例
选取实际采集地震数据验证本文方法的适用性。图8为M区海上二维原始地震数据及其振幅谱,道间距为25m,采样率为4ms,180道接收。本文方法基于傅里叶变换,只适应线性或近似线性同相轴地震数据重建,而对于非线性同相轴,通常采用分窗口重建。
为满足处理要求,从原始数据中截取第100~第140道数据,时间轴方向截取0.8~1.6s(图9a、图9b)。对该窗口数据进行50%的规则欠采样(图9c),可见规则采样引起的假频信息(图9d)与真实频谱(图9b)非常相似。

图8 现场实测数据(a)及其f-k谱(b)
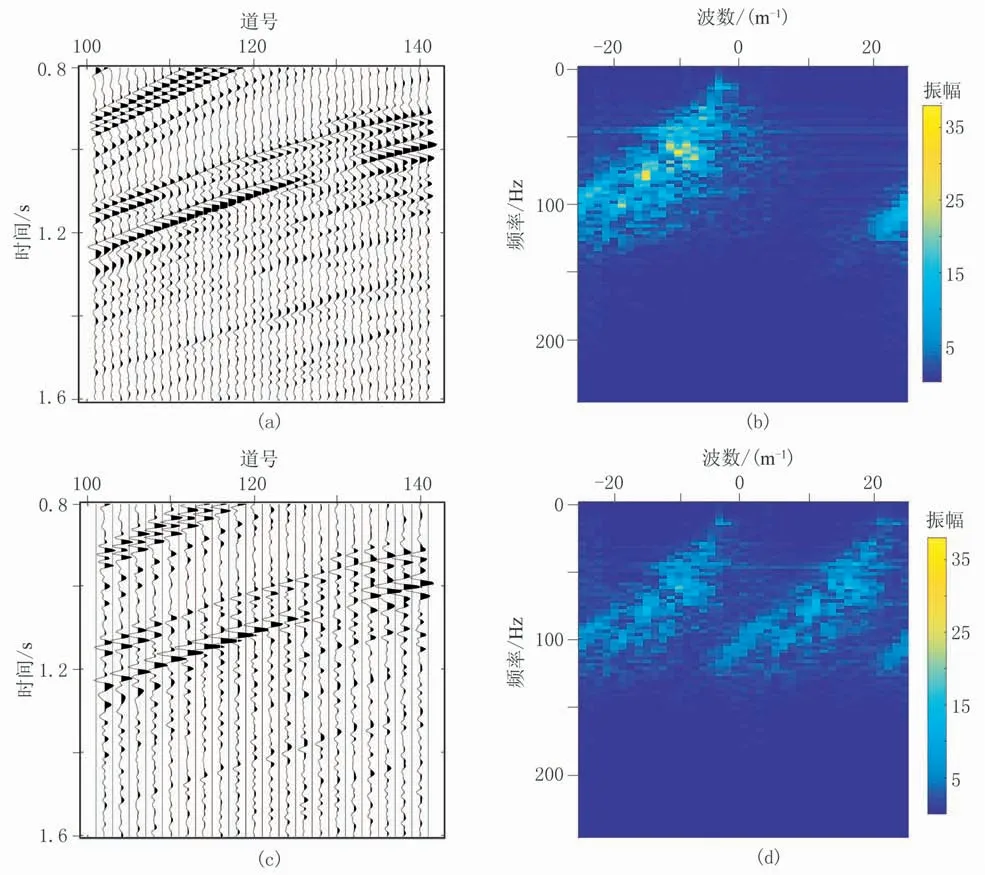
图9 截取数据和规则缺失数据及其f-k谱
针对该实际数据体,本次选取选择函数中计算倾角p值的范围是-12~12。选择函数以图9d中原点为起点,对频域中的能量进行扫描,扫描的同相轴能量分布如图10所示,此扫描范围可最大程度地保留反射波同相轴能量、去除规则采样产生的假频信息。同时,迭代次数和阈值函数ε值的选取也影响重建效果。
由最终重建结果(图11a)及对应f-k谱(图11b)得到重建结果误差(图11c)及其频谱(图11d),可见规则采样导致的假频信息得到较彻底压制,并保留了主要反射波同相轴能量,重建结果的信噪比为12.78d B。

图10 实测数据的规则缺失50%数据f-k域选择函数

图11 重建结果及其f-k谱
4 结论与讨论
本文结合傅里叶变换与POCS重建算法,研究了倾角扫描选择函数,该函数对全频段的能量轴进行扫描,确定出主要倾角;并把该函数引入传统的重建算法,重建线性或近似线性的同相轴数据;在此基础上,将该方法应用于理论和实际数据,重建出规则缺失的地震数据并压制了假频干扰。
根据对倾角扫描选择函数的分析,在传统傅里叶变换和POCS重建算法的应用中,只可重建线性或近似线性的地震数据。然而,实际数据中缺失的反射波同相轴往往是非线性的,此时需对非线性地震数据做分窗口重建,使得每个窗口内地震数据满足近似线性同相轴。
还可尝试选取另一种数学变换替代傅里叶变换,并结合倾角扫描选择函数,重建非线性同相轴缺失数据。这将是后续研究课题。
