初中生成绩数据的相关性分析及综合评价研究

田 萌 许 超

0 前言

随着数据收集和存储方式的更新和计算机技术的飞速发展，数据挖掘成为一个日益活跃的研究领域。自2008 年首届国际教育数据挖掘大会成功召开以来，教育数据挖掘成为教育领域大数据应用的一个研究热点。学生成绩是评估学校教育质量的重要依据，也是评价学生是否掌握所学知识的重要方式，传统成绩数据处理多关注平均分和排名，数据背后隐藏的大量信息通常被忽略。利用数据挖掘技术发现成绩数据隐藏的内在规律，进行个性化的学生指导方案的设计，可助力精准教学研究改革，为提高学生学习成绩、提升教师教学效果和提速学校管理效率提供有力的技术支持[1]。

近些年来，国内外针对教育数据挖掘的研究成果比较丰富。从国际研究情况看，Bhardwaj、AL- Radaideh、Hijazi 等人曾分别针对印度、约旦、巴基斯坦等国家的大学生课堂表现，收集学生课堂测试、期中考试、期末考试等过程性成绩，借助聚类算法分析并预测其学习成绩[2-5]。从国内研究情况看，目前教育数据挖掘研究多集中于大学教育阶段，研究多立足于利用数据挖掘技术实现课程关联分析、课程成绩预测和学生就业指导等。开展中学教育数据研究较多的是华东师范大学、华中师范大学、上海师范大学及西北师范大学等高水平师范类院校。[6-8]这些文献选择的成绩数据处理角度各有不同，而本文主要针对学生的成绩数据，利用数据挖掘算法分析学生的学习状态和学习优势，提升学生学习信心，找准学生学习薄弱点，为学生的全体发展与整体素质提高保驾护航。

1 预备知识

相关分析是一种探讨变量间的相关关系的通用统计方法，最常见的单因子相关分析法就是相关系数法。单因子相关分析法可用来发现两个因子变量间的相关关系，当考察两组对象间的关系时，就需要采取多因子相关分析法，例如典型相关分析方法。典型相关分析方法是求解在约束条件a'Var（x）a=1 与b'Var（y）b=1 下，使得x 的线性函数U=a'x 和y 的线性函数V=b'y 的相关系数最大时的方向a 与b。

聚类分析利用数量化方法描述事物之间的相似程度，它作为一种定量方法将从数据分析的角度，给出一个更准确、细致的分类工具。通常大家利用距离来度量样本点间的相似程度。层次聚类是一种聚类算法，它基于距离度量可以创造出一棵条理分明的多层次积聚的聚类树。

2 实验设置

2.1 数据集描述

本文数据取自淄博市一所公办初等中学，所考察年级学生共582 名，本次实验选取本级部三次集中考试成绩，共包含12个平行班，没有设置重点班和非重点班。因为考试监考纪律严格，阅卷流程规范，所以成绩可视作真实有效。为保证数据处理时的规范性，在去除了缺失数据的信息后，最终保留了569 名学生的数据记录。

2.2 数据集预处理

本市初中生开设多门学科，因不同学科的总分不同，为减少计分方式对成绩分析的影响，我们对学生每门课的成绩进行归一化，得到学生每门课程的规范成绩。基于规范成绩，8 门课程的成绩平均值和标准差汇总在表1。

从表1 可以看出，8 门课程中英语得分率最高，地理得分率最低。从标准差上来看，地理、数学与生物的个体间差异较大。数学课一直是学生学习能力的一个试金石，进入初中教学内容的突然增多，对计算能力日益严格使得学生成绩间的差距不断增大。地理与生物是初中新上课程，且综合性较强，很多仍固守小学阶段考前背一背习惯的学生，往往不能得到较好的成绩。这说明升入初中后学生的学习习惯和学习主动性对学习成绩有着较大的影响。

表1 8 门课程的成绩平均值与标准差

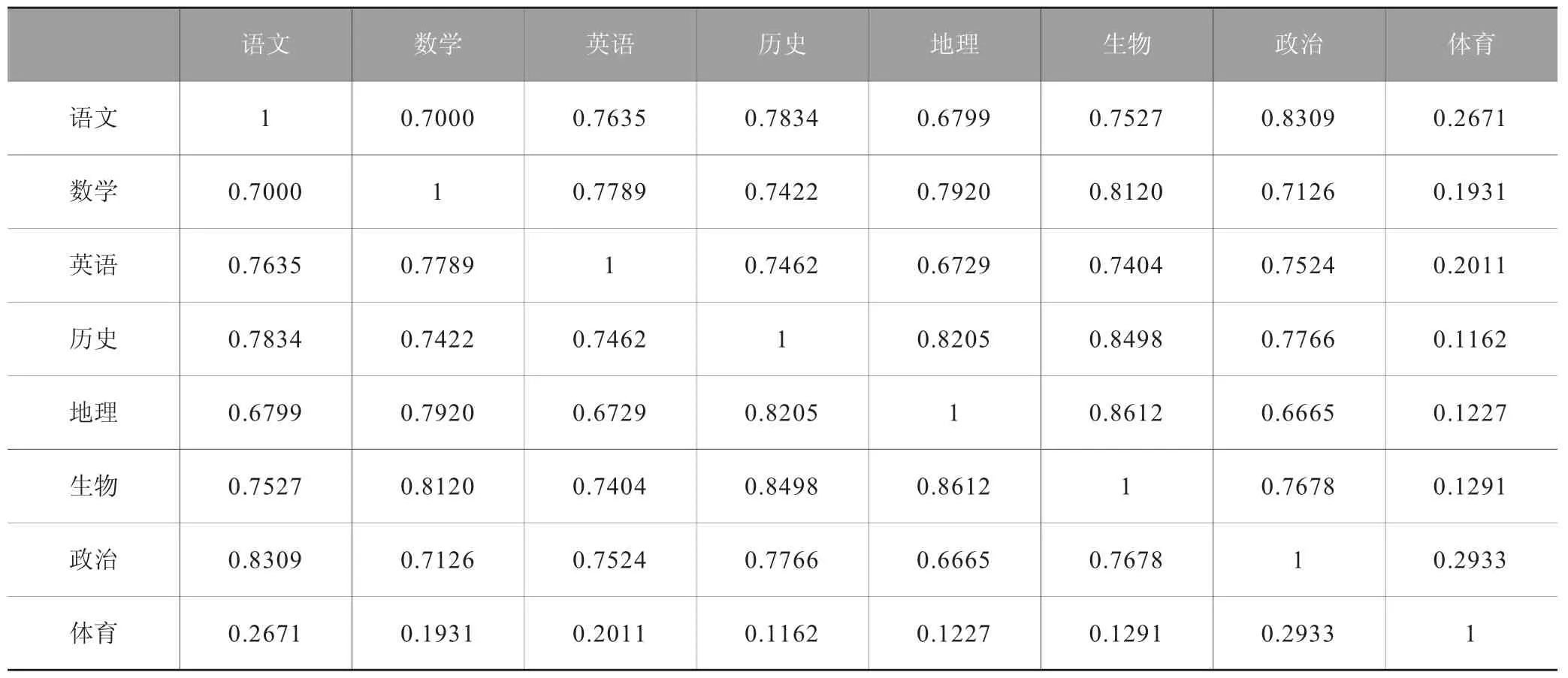
表2 课程间的相关系数

2.3 课程成绩相关性分析

本节分别应用相关系数法和典型相关分析法进行不同课程的单因子相关分析和多因子相关分析。基于归一化后的数据，我们利用MATLAB 软件得到8 个课程间的两两相关系数。见表2 。

表2 中粗体数据标出了每门课程与其线性相关程度最高的课程，从中可以看出历史、地理与生物的成绩相关性较高，这是因为在初一阶段此这三门课均属于副科，课时较少，所以成绩往往能客观反映学生的学习积极性与学习态度。语文与政治的成绩线性相关性最大，其原因可能在于这两门课程都偏重文字记忆及文章和段落的理解。数学与生物及地理的成绩相关性较大，部分原因在于这些课程都偏重逻辑推理能力。

图1 不同类课程间的典型相关图

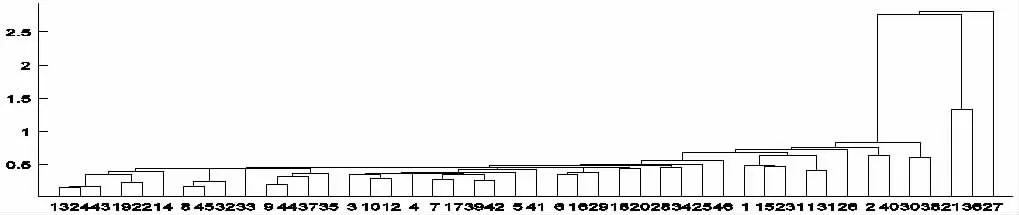
图2 样本班级学生成绩模糊动态聚类图

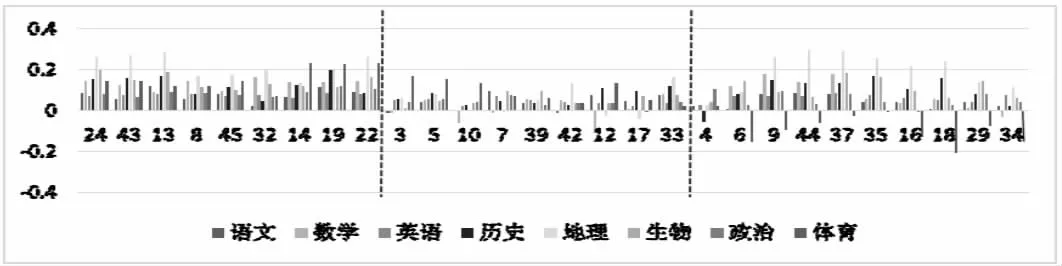
图3 簇1-簇3 学生规范成绩数据差1 后柱形图

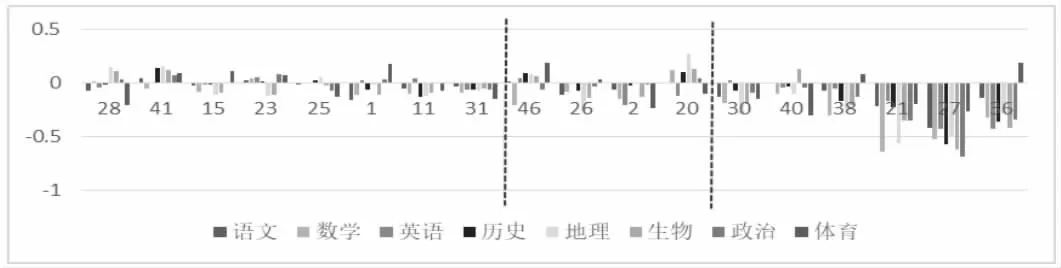
图4 簇4-簇6 学生规范成绩数据差1 后柱形图

除了单门课程间的成绩相关性分析，将语数外三科化为一组，史地生政化为一组，体育单列一组，找出不同类课程间的典型相关系数，经MATLAB 计算得出语数外与史地生政的相关系数为0.9116，史地生政与体育的相关系数是0.3512，语数外与体育的相关系数为0.2675，其示意图见图1。

从中可看出，语数外成绩与史地生政成绩密切相关，这说明对多数学生而言，学习能力、学习态度在文化课科目中的表现是比较一致的。体育成绩是一个比较独立的存在，这也提醒广大的家长及学生应注重各项体育锻炼的开展，提高身体素质，全面提升整体素质。

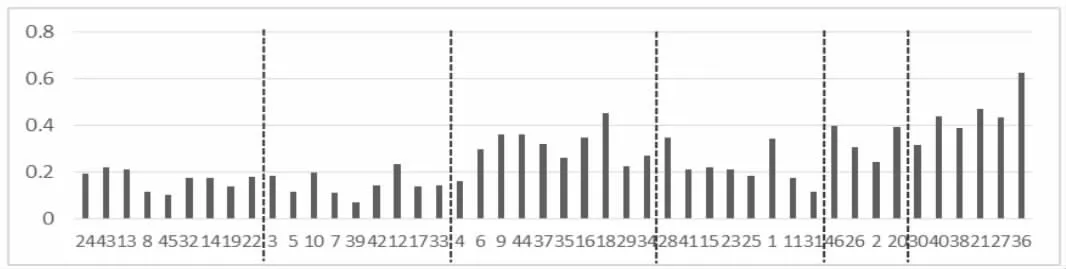
图5 学生规范成绩的区间长度柱形图

2.4 学生个体聚类分析

为研究学生个体的成绩，分析其优劣势学科，制定个性化指导方案，帮助授课教师提高教学效果，本文采用多元统计分析中的层次聚类方法，以6 班学生为例，分析学生的聚类效果。本班共有有效成绩的学生46 人。

从图2 中可以看出，本班学生除5 名学生外，其余学生间的相似度比较高。通过观察模糊动态聚类图，自主将这些学生分成6 个簇，见图3 及图4。图中不同的簇之间用虚线进行分开。

通过观察图3- 图4，可看出不同簇类间的细微差别。例如，第一簇类学生成绩相对比较均衡且成绩较高，第二簇类学生成绩依旧比较均衡，但相比第一簇类成绩稍逊一些，第三簇类学生的多数课程成绩较高，但成绩不算均衡，有瘸腿课程，第四簇类学生的成绩较均衡，但是多数成绩稍逊于均值，第五簇类学生的成绩相比第四簇类各科成绩表现更低一点，第六簇类的学生不及格科目较多，且成绩离均值更远。

为展示学生不同课程间的差异，令每名学生成绩中的最大值减去最小值，得到该学生的成绩区间长度，见图5。从图中可以看出，第一簇与第二簇学生成绩均衡性较好，这两类学生老师应积极鼓励，随时注意学生的学习状态，进一步发觉有兴趣的学科，帮助其有效提高学习成绩。第三簇与第四簇学生的不同科类成绩差异较大，说明该簇学生有较明显的优势学科，针对这类学生老师应因势利导，鼓励该簇学生补齐弱势学科，实现总体成绩的较大提升。第五簇及第六簇学生，老师应多鼓励，在课上及课下关注他们的心理健康及身体健康，鼓励他们发现学习兴趣点，找到学校教育的快乐，建立自信心。

3 结论

挖掘学生成绩所隐含信息，能更科学客观地评价学生的学习状况，在模糊掉社会所敏感的排名的同时，让家长清楚看到孩子年级或班级的学习状况，找准学生的弱势学科，进而有针对性的帮助孩子查缺补漏，提高成绩。