浅谈微课的线性代数教学设计——以向量组的秩为例

凌征球 覃思乾

0 引言

玉林师范学院是一所升本的地方应用型高校，有近2 万人的在校生和10 大学科门类，目前在全校的理工类专业中都开设有线性代数课程，每年选课学生在2000 人上下[1]。由于课程概念的严密逻辑性与理论性、计算的繁杂与难度较大等原因，造成学生的学习出现不少的困惑使得总体的教学效果并不乐观。多年来，为了改变这种状况与提高教学效果，不少专业教师尝试着多种不同的教学方法。

与此同时，随着计算机网络技术的迅速发展，特别是2020 年春季的新冠肺炎疫情的爆发使得QQ 直播、MOOC 课堂，微课等多种线上学习方式得到了很大的推进，知识的学习与取得受到时间与空间限制的途径已大为改观。

本文将针对玉林师范学院的具体情况，在线性代数教学中如何嵌入微课的线上学习方式进行教学设计展开探讨。首先给出目前线性代数课程教学的现状分析。

1 线性代数教学现状

1.1 教学手段与方法依然单一

因为专业的基础要求，线性代数一般安排在大学一年级授课。此外教师基本采取“黑板+PPT+讲授”的教学模式，同时在教学过程中强调课程内容的逻辑性与严密性，教师讲得多而学生做得少。久而久之，导致的结果就是学生的被动学习，造成一些重点与难点内容不能完全理解而无法掌握。

1.2 课程内容多课时少

在一般情况下，线性代数课程包含行列式、线性方程组、矩阵与二次型等基本内容，但课程只有32 课时。直接的结果就是教师应在黑板上板书的过程只使用PPT一闪而过，使得学生对知识内容的理解如概念定理一知半解，而计算题往往只到模仿的程度却对所得结果的得来缘由不太明白。

1.3 教材不符合学生的实际水平

玉林师范学院属于地方二本院校，学生每年录用分数基本上处于420-440 分之间，由此便可以看出学生的总体水平特别是数学基础不是很好。而使用的教材偏重理论而且课程内容缺乏渐续推进由浅到深的整个过程，此外课本例题与习题的计算基本上都涉及分数的通分计算，而这些正是学生本身的不足，导致了部分学生逐渐失去了对线性代数的学习兴趣。

正是因为有上述主要原因的存在，学校的线性代数课程教学与教学效果不理想。如何探讨与改善该门课程的教学手段与方式努力提高教学质量，成为在职数学教师一个迫切需要解决的首要任务。

伴随着半导体芯片技术的发展成长的智能手机的应用已经越来越广泛，直接导致了“互联网+ 课程”的推进，特别是2020 年春季新冠疫情的爆发使得线上教学与学习得到了充足的应用环境，知识的获取受到时间与空间的限制影响大为降低。目前，“微课”以其“精、小、短”的特色在大中小学的教学过程中的应用得到社会的肯定[2-3]。一般认为，微课具有以下特色。

2 微课的特色

微课就是微型教学视频为载体，针对学科的一个知识点的在线网络视频课程[4]。其具有如下的主要特色：

（1）内容精选有针对性

通常情况下，微课都是针对学科知识的重点或难点展开的。对线性代数的课程来说，微课则集焦于基本概念、定理的讲述或者计算方法的过程介绍。学生可以反复观看学习，逐个掌握与理解知识点，提高学习效率。

（2）时间短利于灵活学习

一个微课的时间通常介于10- 15 分钟，时间短容量小，方便学生随时在碎片式的时间使用，增加他们自主学习的能力与学习兴趣。

（3）使用设备与平台有多种选

微课可以在台式与笔记本电脑、智能手机、平板等多种设备上使用，也可以采用QQ、微信、MOOC、钉钉等平台上播放。

3 微课的线性代数教学设计例

针对线性代数中向量组秩的概念，我们给出了微课的教学设计过程与方法。

（1）设计理念

向量组的秩属于线性代数的一个难点内容，涉及线性相关与线性无关、向量的线性表示与极大线性无关组，后续可推广到矩阵的秩与向量空间的维数等概念。因此，理解与掌握的程度直接影响着后面知识的学习。我们设计的理念与思路是：引例的讲解与总结；引入秩的概念；引申思考。

（2）教学过程设计

首先是引例的讲解：假设有如下的一组向量

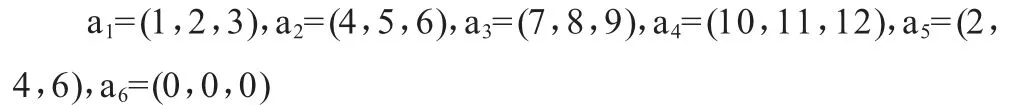
要求从这组向量中找出线性无关的一部分，试问：最多能够找出多少个向量？

第1 步：先找一个非零向量，因为单独非零向量属于线性无关。依此我们可以从a1，a2，a3，a4，a5中任取一个作为第1 步的选择。不妨取向量a1。

第2 步：由于不成比例的两个向量是线性无关的。因此，我们从剩下的5 个向量中再取一个跟a1不成比例的向量，如此可选取a2，a3，a4之中的一个。不妨取向量a2。

由上两步，我们取出部分的向量a1，a2是线性无关的。

第3 步：从剩下的4 个向量中任取一个加到a1，a2中，还有线性无关的吗？此时有4 组情况，分别是：a1，a2，a3；a1，a2，a4；a1，a2，a5；a1，a2，a6

由于这4 组向量组成的行列式

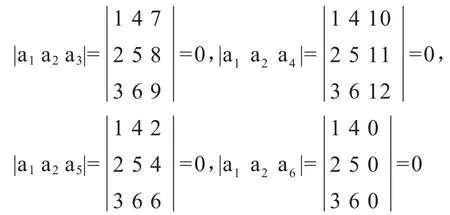
因此，它们都是线性相关的。由此得到问题的结论：“在这个向量组中，线性无关的向量最多是2 个向量。”

自然就有个问题：是否存在其他的答案。

为此，我们重复第1 步取向量a2；重复第2 步选向量a3；然后重复第3 步就有下列4 个向量组：

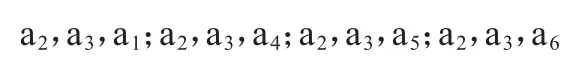
经过计算这4 个向量组构成的行列式，知道这些向量组都是线性相关的。

由此确定上述得到问题的答案是正确的。

引例的总结：

①得到的向量a1，a2或者a2，a3称为向量组a1，a2，a3，a4，a5，a6的一个极大线性无关组

②极大线性无关组可能不唯一，但所含向量的个数相同。

③这个相同的个数，称为向量组的秩。

其次是引入相关概念：

如果向量组ai1，…，ais是向量组a1，a2，…，ar的一部分，并且满足下列条件：

①ai1，…，ais是线性无关的；

②从a1，a2，…，ar去除ai1，…，ais后任取一个向量添加到向量组ai1，…，ais后都线性相关。那么ai1，…，ais就称为a1，a2，…，ar的一个极大线性无关组。

极大线性无关组所含向量的个数，称为向量组的秩。

最后是引申思考：

由a1，a2线性无关而a1，a2，a3线性相关知道，向量a3可以用向量组a1，a2线性表示。得到：

不是极大线性无关组的向量，都可以用极大线性无关组线性表示，而且表示是唯一的。

4 结语

将微课应用于线性代数的教学，切忌不是完全使用微课取代课堂教学，而只是作为一种补充手段。把课程学习的每一个关键知识点制作成微课，可以方便学生随时学习，达到提高教学质量与效率的目的。