高速列车头车气动噪声的控制方法研究

姜世杰，杨 松，张博宏，闻邦椿

（东北大学机械工程与自动化学院，辽宁 沈阳 110819）

1 引言

随着技术水平的发展，列车的运行速度极大提高，致使一些在低速时可以被合理忽略的问题变得尤为突出，并严重制约着列车高速技术的发展。铁路高速化中最严重的问题之一莫过于噪声的影响，此噪声主要包括轮轨噪声和气动噪声[1-2]。目前，铁路轮轨噪声已得到了有效的控制，但列车的高速运行使得气动噪声成为铁路噪声中最为重要的组成部分[3]。现有研究表明[4]，当运行速度达到250km/h 及以上时气动噪声将超过轮轨噪声，成为列车最主要的噪声源。急剧增大的气动噪声给乘客的舒适度和铁路沿线居民的日常生活带来极大的负面影响，甚至造成周围各类设备和建筑物等的疲劳破坏，极大地制约着高速铁路的进一步发展。为此，研究高速列车气动噪声的控制方法具有十分重要的意义。

在噪声频率分布方面[5]，研究结果表明列车的气动噪声属于宽频噪声，即在较宽的频带内分布，无明显的主频；并且其在低频范围内噪声能量较大，而在高频范围能量则较小。因此对于噪声阻断方面，声屏障对高速列车气动噪声的减弱作用不大，甚至可能会使得屏障与列车之间的噪声值上升，降低乘车舒适性。所以，从源头针对列车进行气动噪声的改进具有普适性。由于车头附近的表面状态变化集中，并且沿表面的气流大，导致在该处产生剧烈的空气湍流并形成噪声，成为主要气动噪声源之一[6]。因此，针对列车的车头进行有效的改进，将对降低和控制其气动噪声产生明显的效果。

提出了针对高速列车外流场气动噪声的车头改进方案，并进行了相应的仿真计算，分别完成了稳态流场、列车表面噪声源和瞬态流场的计算，进而获得了远场气动噪声的仿真结果；通过对比分析不同形式的头车气动噪声的仿真结果，确定了车头改进的有效性和最佳方案。

2 车头改进

为了降低高速列车气动噪声，提出了9 种不同形状的车头改进方案，通过研究不同车头形状对远场气动噪声的影响，以确定改进方案的可行性和有效性。不同形状车头的示意图，如图1所示。纵向截面共分三种：其中，A 型车头前端与水平面夹角为45°；B 型车头前端与水平面夹角为25 度；C 型车头前端与水平面夹角为15°；横向截面也分为三种：其中1 型车头两侧面夹角为140°；2 型车头两侧面夹角为 80°；3 型车头两侧面夹角为 60°。由于只分析车头流线型对远场气动噪声的影响，并且气流通过车头13m 以后趋于稳定，车尾流场对车头流场的影响可以忽略，因此将头车之后车厢全部略去，以减少网格划分数量，加快仿真计算时间。

图1 不同车头的纵向截面和横向截面Fig.1 Train Heads with Different Longitudinal and Cross Sections

模型的长、宽、高尺寸分别为25700mm，3400mm 和3700mm，为了进一步提高计算效率，保证结果只取决于车头流线型的影响，模型略去车窗、车门、转向架和受电弓等部分，如图2 所示。

图2 改进的头车模型Fig.2 Improved Train Heads Model

为保证流场边界域不对流场产生影响，车外流场模型需足够大。将流场域定义为长方体，入口边界距离车头20m，出口边界距离车尾90m，侧面边界距离车身中线20m。因为模型为对称体，为便于计算，取模型对称的一半做分析。

采用混合网格法对模型进行网格划分，车身表面采用三角形和四边形单元，空间流场域采用以四面体为主，六面体单元为辅的网格划分策略。由于车身表面气体流动复杂，故列车表面生成3 层三棱柱形边界层，第一层厚1.25mm，每层按照1：1.2 的比例增加，总网格数约为500 万个，如图3 所示。

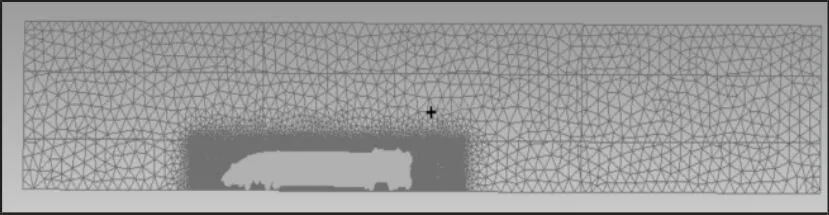
图3 模型和流域网格划分Fig.3 Model Mesh Structure of Car and Flow Field

3 仿真计算方法

高速列车气动噪声的仿真计算主要包括：首先，应用Realizable k-ε 湍流模型计算稳态流场；再次，基于稳态流场的计算，采用宽频带噪声模型计算列车表面的气动噪声源；然后再基于稳态流场的仿真，利用大涡模拟（LES）方法研究瞬态流场的计算，获得车身外表面的脉动压力；最后，基于瞬态流场的仿真，应用Lighthill 声类比理论完成列车外流场气动噪声的计算。

3.1 稳态计算

目前，由于高速列车的运行速度远低于声速（340 m/s），马赫数远小于1，因此，周围空气可当作粘性不可压缩流体计算，其基本控制方程如下：

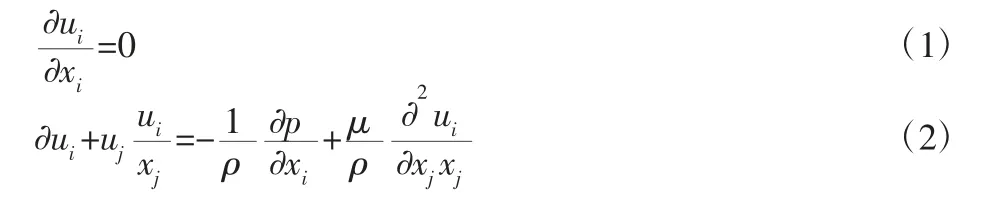
式中：u—列车周围流场的空气速度的分量；x—模型的直角坐标分量；p 和ρ—列车周围流场的空气压力和空气密度；μ—空气动力黏度。

稳态计算是基于Realizable k-ε 两方程湍流模型开展的[7]。选用该模型是因其适用的流动类型更为广泛（如有旋均匀剪切流、腔道流动和边界层流动等），且模拟结果相较于标准的k-ε 模型更为准确。Realizable k-ε 湍流模型关于k 和ε 的输送方程为：

式中：xi，xj—位置矢量；ρ—气体密度；σk—常数 σk=1.0；Gk—由于平均速度梯度而产生的湍流动能；Gb—由浮力而产生的湍流动能；σε—湍流动能耗散率普朗特数σε=1.2；E—源项；C1=max应力变化率张量。

稳态流场仿真计算中的主要参数设置，如表1 所示。

表1 稳态设置Tab.1 Steady State Setting

3.2 噪声源计算

高速列车气动噪声没有明显的频段，属于宽频带噪声，即噪声能量是在一个宽频段的范围内呈连续分布的状态。在较低马赫数和较高雷诺数下，Proudman 利用声学类比理论，对单位体积内各向同性湍流所辐射的声功率进行了推导[8]，其表达式为：

式中：α—模型常量；u—湍流速度；l—湍流尺度；c0—声速。用 k、ε 的形式，可分别表示成。

Hussaini 和Sarker 针对各向同性湍流进行了直接数值模拟分析[7]，获得αε的值为0.1。基于湍流模型的稳态计算，提取流场中各节点的湍流动能和湍流耗散率，计算出各个节点处的声功率，从而获得整车表面的声功率级分布云图。

3.3 瞬态计算

基于N-S 方程在物理空间的滤波分析推导得出的大涡模拟（LES）模型的控制方程，开展了瞬态仿真分析[2]。该过程将小于设定过滤宽度的涡旋去掉，而只保留大的涡旋，从而得到其控制方程为：

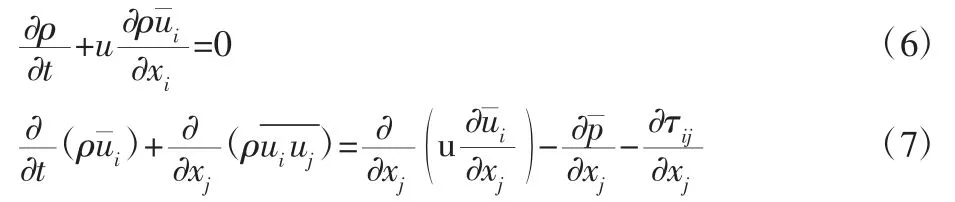
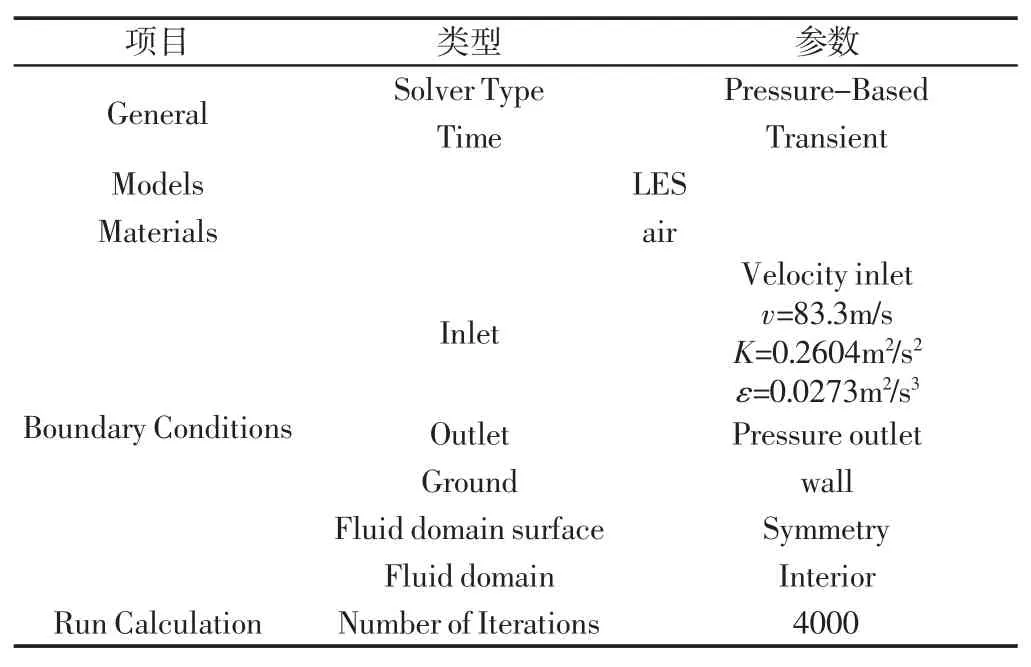
表2 瞬态设置Tab.2 Transient State Setting

3.4 远场气动噪声计算

高速列车远场气动噪声计算采用Lighthill[9-10]推导的声比拟理论方法进行研究。根据连续性方程和N-S 方程，声传播方程为：

式中：Tij—lighthill 湍流应力张量-eij，eij—流体的粘性应力张量 ρ′=ρ-ρ0，p′=p-p0，ρ0和 p0—未受扰动时的流体密度和流场压力的均值，ρ′和p′—流体密度和流场压力的波动值。

当非定常流动区域存在固壁边界时，Curle 导出Lighthill 方程的解为：

式中：x—测声点矢量；t—时间；y—声源点矢量；nj—垂直列车外壁向外（指向外流场）的方向余弦；R=x-y；Pij—空气对车身外表面的脉动压力。

上述等式（9）中包含了两类噪声源[11]，等号右边第一项代表表面偶极子声源（源于列车周围流场内部的Lighthill 应力）；第二项为体积四极子声源（源于物体的表面压力与黏性剪切应力）。由于列车的偶极子声源和四极子声源所产生的气动噪声分别与马赫数的三次方和五次方成正比，因此，四极子声源与偶极子声源所产生的噪声之比与马赫数的平方成正比。所述的高速列车的运行速度在300km/h 左右，相较于声速而言是很低的，其马赫数仅为0.245，进而高速列车的四极子声源所产生的气动噪声相对较低，可忽略不计[11]。由此，高速列车外流场气动噪声的计算式（9）可以表达如下：

式中：P—声压；P0—参考声压，P0=2×10-5Pa。

由此可知，高速列车远场气动噪声的声压可由车身表面脉动压力求得。根据瞬态计算结果，提取车身表面各个节点的脉动压力数值，再根据式（11）便可获得高速列车远场气动噪声的声压预测值。在流场域中沿车身方向共均匀布置了21 个监测点，两点间距为2m，每个监测点距离列车轴中心线和车底分别为7.5m 和3.5m，其中第一个监测点距头车鼻尖沿车身方向为5m，如图4 所示。

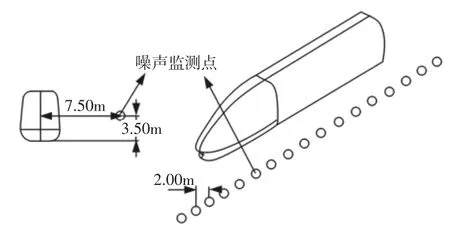
图4 远场噪声监测点排布图Fig.4 Monitors Location

4 结果分析

以头车鼻尖为坐标原点，车身长度方向为横坐标轴正方向，在相同纵截面情况下，不同的横截面对远场气动噪声的影响，如图5 所示。由图5（a）可知，当车头纵向截面为A 型时，1 型横截面头车外流场气动噪声平均值最大，3 型横截面头车气动噪声平均值最小，为108dB。在鼻尖附近，1 型和3 型横截面头车气动噪声的声压级峰值分别为117dB 和102dB，差值达15dB。

可见，在车头纵截面相同的情况下，车头两侧面夹角越小，即横截面鼻尖处越窄，在鼻尖附近所产生的远场气动噪声声压级峰值越小，整个头车的气动噪声平均值也越小；此外，在3 型横截面下，鼻尖处已不再出现突变声压级峰值。由图5（b）和图5（c）可知，当车头纵向截面分别为B 和C 型时，横截面的影响均符合上述规律。

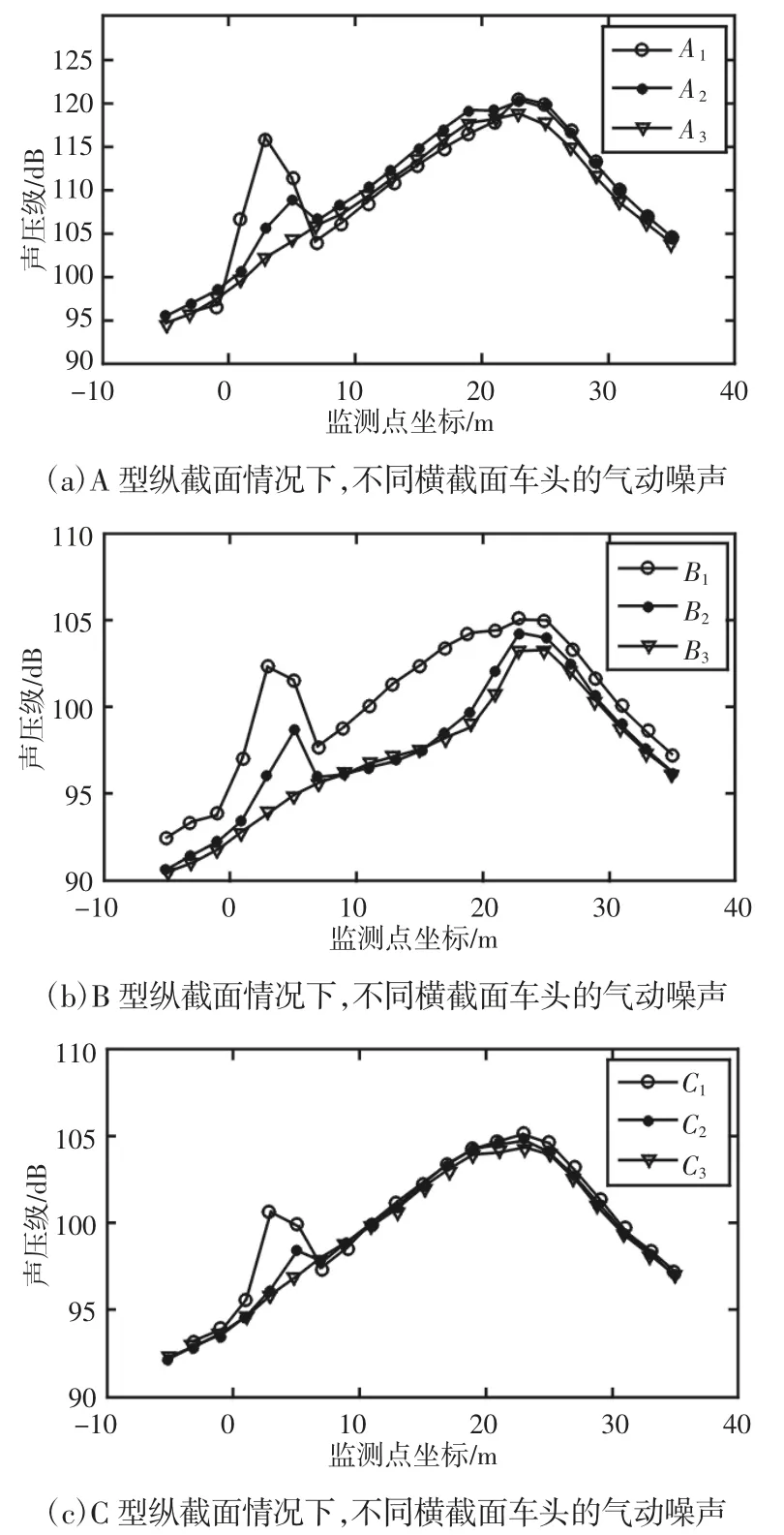
图5 不同横截面对相同纵截面头车气动噪声的影响Fig.5 Influence of Different Cross Sections on Aerodynamic Noise Generated by the Train Heads with the Same Type Longitudinal Section

在相同横截面情况下，不同的车头纵截面对头车远场气动噪声的影响，如图6 所示。可以看出，在1 型横截面（车头两侧面夹角较大，横截面较宽）情况下，不同的纵截面对气动噪声的影响较小，即声压级数值趋于一致，平均值大约为110dB。在2 型和3型车头横截面情况下，B 型纵截面有效降低了头车的气动噪声，最大差值达10dB。B2 型头车气动噪声的平均声压级为85.1dB，相比A2 和C2 型头车降低了4.5dB；B3 型头车气动噪声的平均声压级为104dB，相比A3 和C3 型头车降低了4.3dB；由此可见，合理的流线型车头的设计将有效降低头车所产生的外流场气动噪声。

气动噪声的平均声压级由大到小的排序为：B1（110.6 dB）＞A（1110.4 dB）＞C（1110.3 dB）＞A（3108.3 dB）=C（3108.3 dB）＞B（3104 dB）＞A（289.6 dB）＞C（289.5 dB）＞B（285.1 dB），由此可见，B2型流线型车头由于其纵截面鼻尖处夹角适中，车头横截面两侧面夹角较小，车头（鼻尖）向车身过渡的曲线平缓，流线型好，因此B2型车头所产生的远场气动噪声的平均值最小，其降噪效果最好。

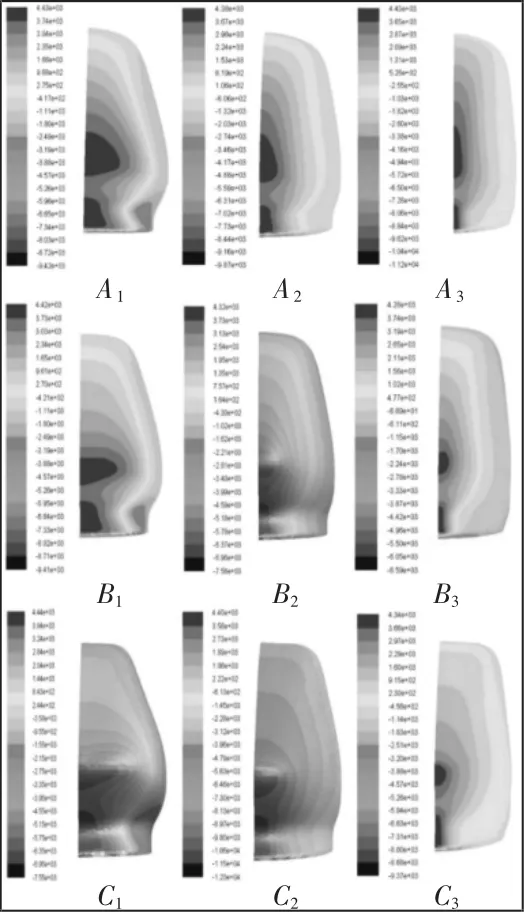
9 种不同流线型头车表面静压云图的正视图，如图7 所示。从图7 中可明显看出：各个模型表面最大静压（红色区域）均为4400 Pa 左右，但A1、B1和C1表面最大静压的面积较大且压力梯度变化剧烈；而 A2、A3、C2和 C3的表面平均静压数值较大；B2和B3的表面最大静压面积都较小且平均静压也较小，但B2的静压梯度变化更加平缓，说明B2型头车流线型最好，进一步说明B2型头车在降低气动噪声方面的优越性。

5 结论

为改善高速列车外流场气动噪声的影响，提出了9 种不同车头形状的改进方案，并进行了仿真分析，具体结论如下：（1）改变高速列车车头的形状，可以有效降低列车头车的外流场气动噪声，本研究可以为高速列车流线型车头的降噪设计提供一定的参考；（2）在车头纵截面相同的情况下，车头两侧面夹角越小，即横截面鼻尖处越窄，在鼻尖附近所产生的远场气动噪声声压级峰值越小，整个头车的气动噪声平均值也越小；（3）车头表面最大静压的面积和平均静压值越小、静压梯度变化越平缓，则车头的流线型越好，降低头车气动噪声的效果越好。